苏教版(2019)高中数学选择性必修第二册课件 9.2独立性检验 课件(共16张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册课件 9.2独立性检验 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 317.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 19:18:49 | ||
图片预览




文档简介
(共16张PPT)
9.2独立性检验
学习目标
通过典型案例的探究,了解独立检验的基本思想和方法.
情景创设
高中生恋爱对学习成绩有影响吗?
高中流行这样一句话“文科就怕数学不好,理科就怕英语不好.”试问:文科学生总成绩不好与数学成绩不好有关系吗?
高中生吸烟对学习成绩有影响吗?
吸烟与患肺癌有关吗?
你能说说下面两个变量之间有关系吗?
调查研究
情景创设
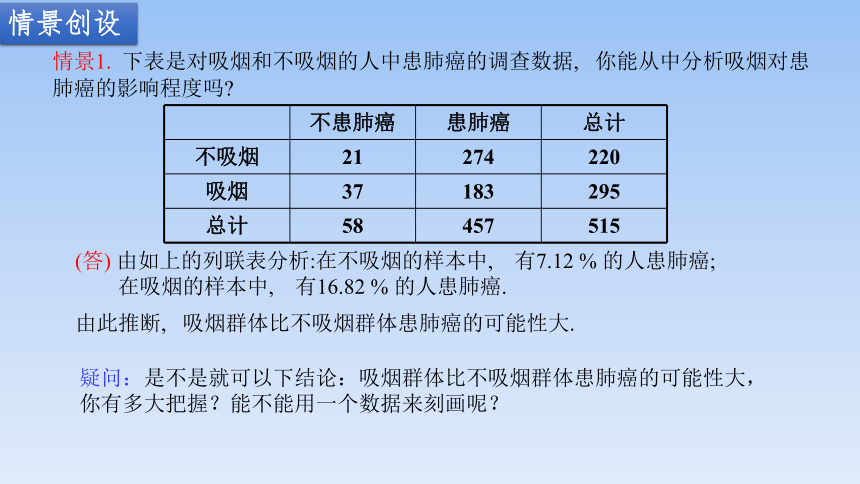
情景1. 下表是对吸烟和不吸烟的人中患肺癌的调查数据, 你能从中分析吸烟对患肺癌的影响程度吗
不患肺癌 患肺癌 总计
不吸烟 21 274 220
吸烟 37 183 295
总计 58 457 515
(答) 由如上的列联表分析:在不吸烟的样本中, 有7.12 % 的人患肺癌;
在吸烟的样本中, 有16.82 % 的人患肺癌.
由此推断, 吸烟群体比不吸烟群体患肺癌的可能性大.
疑问:是不是就可以下结论:吸烟群体比不吸烟群体患肺癌的可能性大,你有多大把握?能不能用一个数据来刻画呢?
数学探究
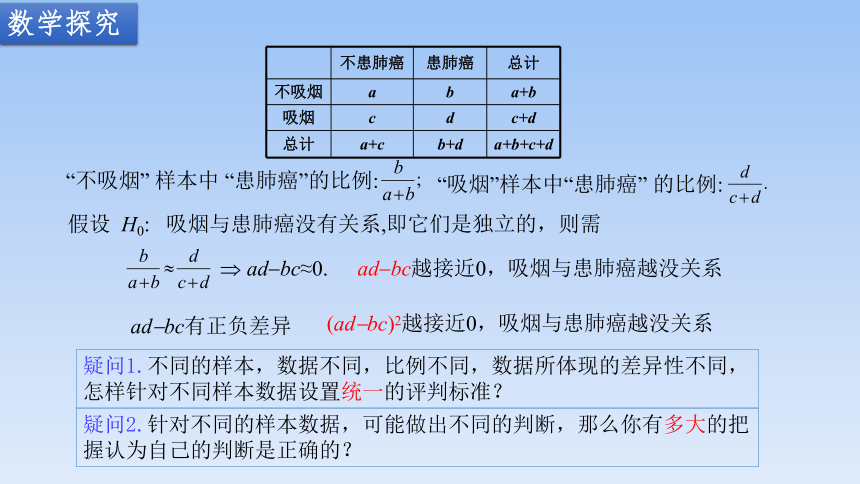
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
“不吸烟” 样本中 “患肺癌”的比例:
“吸烟”样本中“患肺癌” 的比例:
假设 H0: 吸烟与患肺癌没有关系,即它们是独立的,则需
ad-bc≈0.
(ad-bc)2越接近0,吸烟与患肺癌越没关系
ad-bc有正负差异
ad-bc越接近0,吸烟与患肺癌越没关系
疑问1.不同的样本,数据不同,比例不同,数据所体现的差异性不同,怎样针对不同样本数据设置统一的评判标准?
疑问2.针对不同的样本数据,可能做出不同的判断,那么你有多大的把握认为自己的判断是正确的?
数学探究
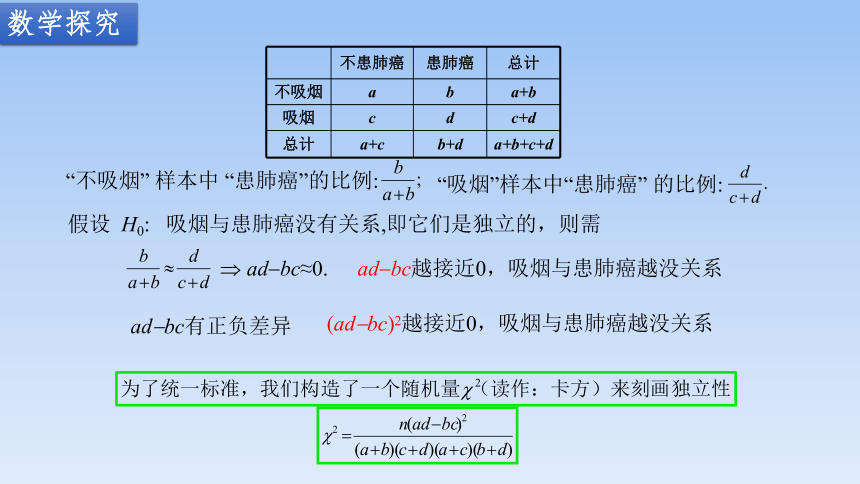
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
“不吸烟” 样本中 “患肺癌”的比例:
“吸烟”样本中“患肺癌” 的比例:
假设 H0: 吸烟与患肺癌没有关系,即它们是独立的,则需
ad-bc≈0.
(ad-bc)2越接近0,吸烟与患肺癌越没关系
ad-bc有正负差异
ad-bc越接近0,吸烟与患肺癌越没关系
数学探究
数学探究
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
记:n=a+b+c+d
假设 H0: 吸烟与患肺癌没有关系,即它们是独立的
频率代替概率
数学探究
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
记:n=a+b+c+d
假设 H0: 吸烟与患肺癌没有关系,即它们是独立的
数学探究
卡方临界值表:
数学建构
数学应用
例 1. 在某医院, 因为患心脏病而住院的 665 名男性病人中, 有 214 人秃顶; 而另外 772 名不是因为患心脏病而住院的男性病人中, 有 175 人秃顶.
能否在犯错误的概率不超过 0.01 的前提下认为秃顶与患心脏病有关系
≈16.373>6.635.
∵P(χ2≥6.635)≈0.01.
患心脏病 患其他病 总计
秃顶 214 175 389
不秃顶 451 597 1048
总计 665 772 1437
∴认为在犯错误的概率不超过 0.01 的前提下, 秃顶与患心脏病有关系.
解:
数学应用
例2、有甲乙两个班级进行一门课程的考试, 按照学生考试成绩优秀和不优秀统计成绩后, 得到如下的列联表:
优秀 不优秀 总计
甲班 10 35 45
乙班 7 38 45
总计 17 73 90
请根据列联表的独立性检验, 能否在犯错误的概率不超过0.01 的前提下认为成绩与班级有关系
解:
≈0.653
<6.635.
∴在犯错误的概率不超过 0.01 的前提下, 不能认为 “成绩与班级有关”.
观察条形图所得的直观判断不可靠.
∵P(χ2≥6.635)≈0.01.
数学应用
例3. 为考察某种药物预防疾病的效果, 进行动物试验, 得到如下列联表:
药物效果与动物试验列联表
患病 未患病 总计
服用药 10 45 55
没服用药 20 30 50
总计 30 75 105
能否在犯错误的概率不超过 0.025 的前提下认为药物有效呢
解:
χ2的观测值为
≈6.109.
查表得 P(χ2≥5.024)≈0.025,
而 6.109>5.024,
所以认为在犯错误的概率不超过 0.025 的前提下, “患病与服用药有关系”.
课堂总结
3、卡方临界值表:
2、卡方公式:
课堂达标
1、在吸烟与患肺病是否有关的检验中,下列说法正确 的是 ( )
A.若χ2>6.635,则有99%的把握认为吸烟与患肺病有关,那么100名吸烟者中,有99个患肺病。
B.从独立性检验可知,有99%的把握认为吸烟与患肺病有关时,可以说某人吸烟,那么他有99%的可能性患肺病。
C.若从统计数据中求出有95%的把握认为吸烟与患肺病有关,是指有5%的可能性使推断出现错误。
D.以上三种说法都不对。
C
课堂达标
2、对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行3年跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示:
又发作过心脏病 未发作过心脏病 合计
心脏搭桥手术 39 157 196
血管清障手术 29 167 196
合计 68 324 392
试根据上述数据比较两种手术对病人又发作心脏病的影响有没有差别。
因为1.780<3.841,我们没有理由说“心脏搭桥手术”与“又发生过心脏病”有关,可以认为病人又发作心脏病与否跟他做过何种手术无关。
解:
9.2独立性检验
学习目标
通过典型案例的探究,了解独立检验的基本思想和方法.
情景创设
高中生恋爱对学习成绩有影响吗?
高中流行这样一句话“文科就怕数学不好,理科就怕英语不好.”试问:文科学生总成绩不好与数学成绩不好有关系吗?
高中生吸烟对学习成绩有影响吗?
吸烟与患肺癌有关吗?
你能说说下面两个变量之间有关系吗?
调查研究
情景创设
情景1. 下表是对吸烟和不吸烟的人中患肺癌的调查数据, 你能从中分析吸烟对患肺癌的影响程度吗
不患肺癌 患肺癌 总计
不吸烟 21 274 220
吸烟 37 183 295
总计 58 457 515
(答) 由如上的列联表分析:在不吸烟的样本中, 有7.12 % 的人患肺癌;
在吸烟的样本中, 有16.82 % 的人患肺癌.
由此推断, 吸烟群体比不吸烟群体患肺癌的可能性大.
疑问:是不是就可以下结论:吸烟群体比不吸烟群体患肺癌的可能性大,你有多大把握?能不能用一个数据来刻画呢?
数学探究
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
“不吸烟” 样本中 “患肺癌”的比例:
“吸烟”样本中“患肺癌” 的比例:
假设 H0: 吸烟与患肺癌没有关系,即它们是独立的,则需
ad-bc≈0.
(ad-bc)2越接近0,吸烟与患肺癌越没关系
ad-bc有正负差异
ad-bc越接近0,吸烟与患肺癌越没关系
疑问1.不同的样本,数据不同,比例不同,数据所体现的差异性不同,怎样针对不同样本数据设置统一的评判标准?
疑问2.针对不同的样本数据,可能做出不同的判断,那么你有多大的把握认为自己的判断是正确的?
数学探究
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
“不吸烟” 样本中 “患肺癌”的比例:
“吸烟”样本中“患肺癌” 的比例:
假设 H0: 吸烟与患肺癌没有关系,即它们是独立的,则需
ad-bc≈0.
(ad-bc)2越接近0,吸烟与患肺癌越没关系
ad-bc有正负差异
ad-bc越接近0,吸烟与患肺癌越没关系
数学探究
数学探究
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
记:n=a+b+c+d
假设 H0: 吸烟与患肺癌没有关系,即它们是独立的
频率代替概率
数学探究
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
记:n=a+b+c+d
假设 H0: 吸烟与患肺癌没有关系,即它们是独立的
数学探究
卡方临界值表:
数学建构
数学应用
例 1. 在某医院, 因为患心脏病而住院的 665 名男性病人中, 有 214 人秃顶; 而另外 772 名不是因为患心脏病而住院的男性病人中, 有 175 人秃顶.
能否在犯错误的概率不超过 0.01 的前提下认为秃顶与患心脏病有关系
≈16.373>6.635.
∵P(χ2≥6.635)≈0.01.
患心脏病 患其他病 总计
秃顶 214 175 389
不秃顶 451 597 1048
总计 665 772 1437
∴认为在犯错误的概率不超过 0.01 的前提下, 秃顶与患心脏病有关系.
解:
数学应用
例2、有甲乙两个班级进行一门课程的考试, 按照学生考试成绩优秀和不优秀统计成绩后, 得到如下的列联表:
优秀 不优秀 总计
甲班 10 35 45
乙班 7 38 45
总计 17 73 90
请根据列联表的独立性检验, 能否在犯错误的概率不超过0.01 的前提下认为成绩与班级有关系
解:
≈0.653
<6.635.
∴在犯错误的概率不超过 0.01 的前提下, 不能认为 “成绩与班级有关”.
观察条形图所得的直观判断不可靠.
∵P(χ2≥6.635)≈0.01.
数学应用
例3. 为考察某种药物预防疾病的效果, 进行动物试验, 得到如下列联表:
药物效果与动物试验列联表
患病 未患病 总计
服用药 10 45 55
没服用药 20 30 50
总计 30 75 105
能否在犯错误的概率不超过 0.025 的前提下认为药物有效呢
解:
χ2的观测值为
≈6.109.
查表得 P(χ2≥5.024)≈0.025,
而 6.109>5.024,
所以认为在犯错误的概率不超过 0.025 的前提下, “患病与服用药有关系”.
课堂总结
3、卡方临界值表:
2、卡方公式:
课堂达标
1、在吸烟与患肺病是否有关的检验中,下列说法正确 的是 ( )
A.若χ2>6.635,则有99%的把握认为吸烟与患肺病有关,那么100名吸烟者中,有99个患肺病。
B.从独立性检验可知,有99%的把握认为吸烟与患肺病有关时,可以说某人吸烟,那么他有99%的可能性患肺病。
C.若从统计数据中求出有95%的把握认为吸烟与患肺病有关,是指有5%的可能性使推断出现错误。
D.以上三种说法都不对。
C
课堂达标
2、对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行3年跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示:
又发作过心脏病 未发作过心脏病 合计
心脏搭桥手术 39 157 196
血管清障手术 29 167 196
合计 68 324 392
试根据上述数据比较两种手术对病人又发作心脏病的影响有没有差别。
因为1.780<3.841,我们没有理由说“心脏搭桥手术”与“又发生过心脏病”有关,可以认为病人又发作心脏病与否跟他做过何种手术无关。
解:
