人教版七年级下册7.2.2 平面直角坐标系下图形面积的计算 课件(共15张PPT)
文档属性
| 名称 | 人教版七年级下册7.2.2 平面直角坐标系下图形面积的计算 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 20:56:48 | ||
图片预览



文档简介
(共15张PPT)
*
平面直角坐标系下图形 面积的计算
*
小结:
1. 已知P(a,b), 则点P到X轴的距离是 , 到Y轴的距离是 。
2. 若A(a,0),B(b,0) ,则AB= ;
若A(0,a),B(0,b) ,则AB= 。
3. 若A(a,c),B(b,c) ,则AB= ;
若A(c,a),B(c,b) ,则AB= 。
已知胡清菁同学的坐标是A(-1,0),郑义科同学的坐标是B(0,3),你能找到自己的坐标吗?
*
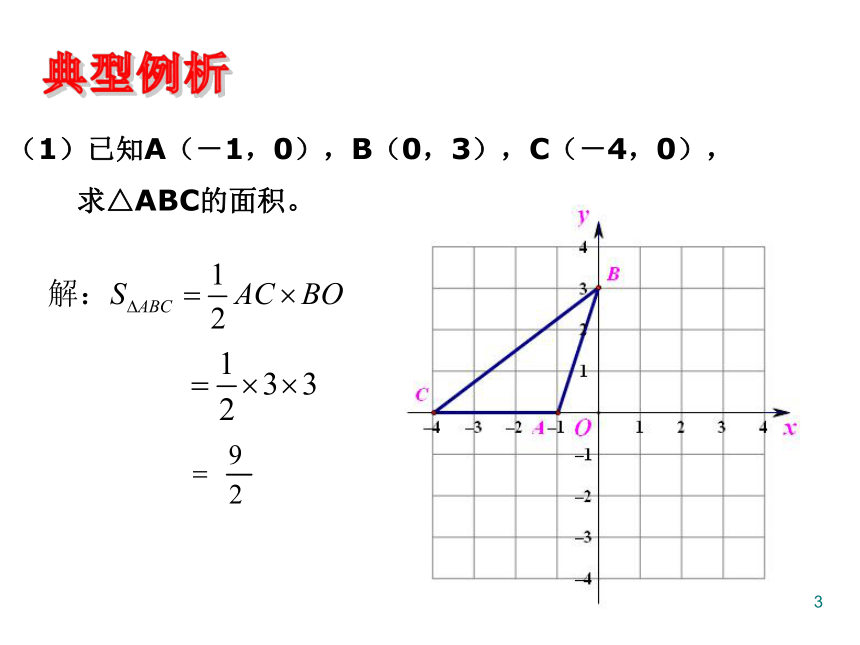
(1)已知A(-1,0),B(0,3),C(-4,0),
求△ABC的面积。
*
(2)已知A(-1,0),B(3,0),C(2,-3),
求△ABC的面积。
小结:求△ABC的面积关键是确 定底和高。
*
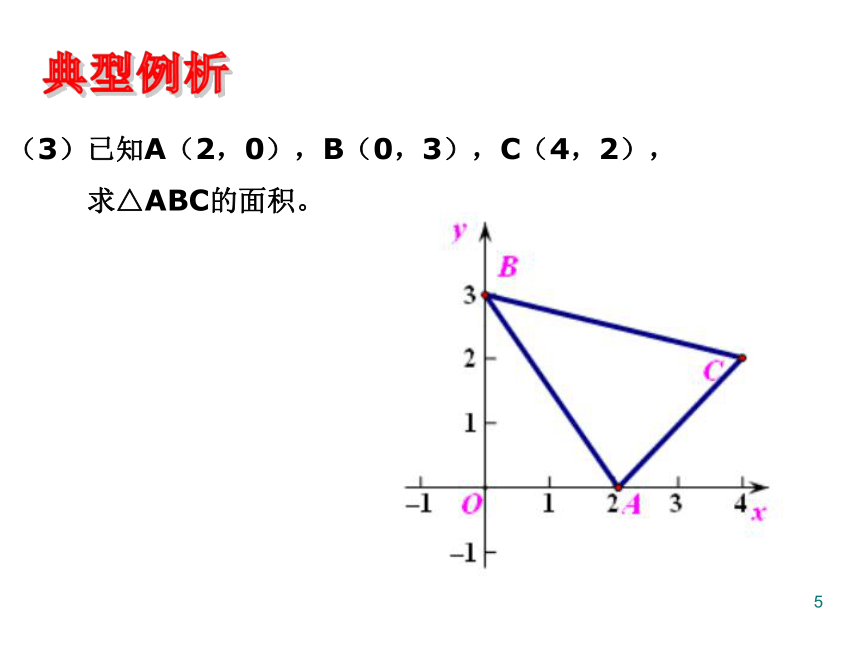
(3)已知A(2,0),B(0,3),C(4,2),
求△ABC的面积。
*
O
y
4
3
2
1
1 2 3 4
A(2,1)
x
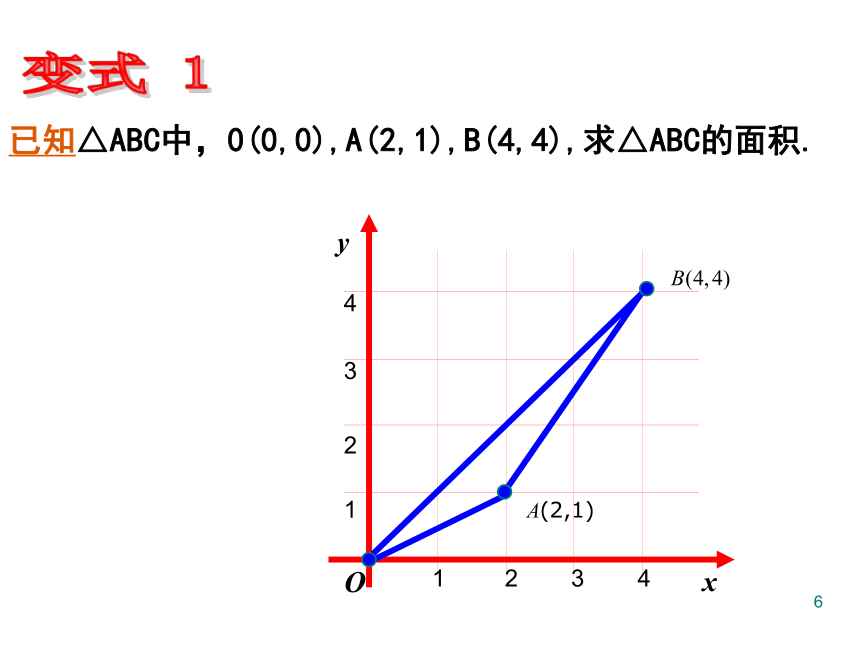
已知△ABC中,0(0,0),A(2,1),B(4,4),求△ABC的面积.
*
O
y
4
3
2
1
1 2 3 4
A(2,1)
x
E(4,1)
F(4,0)
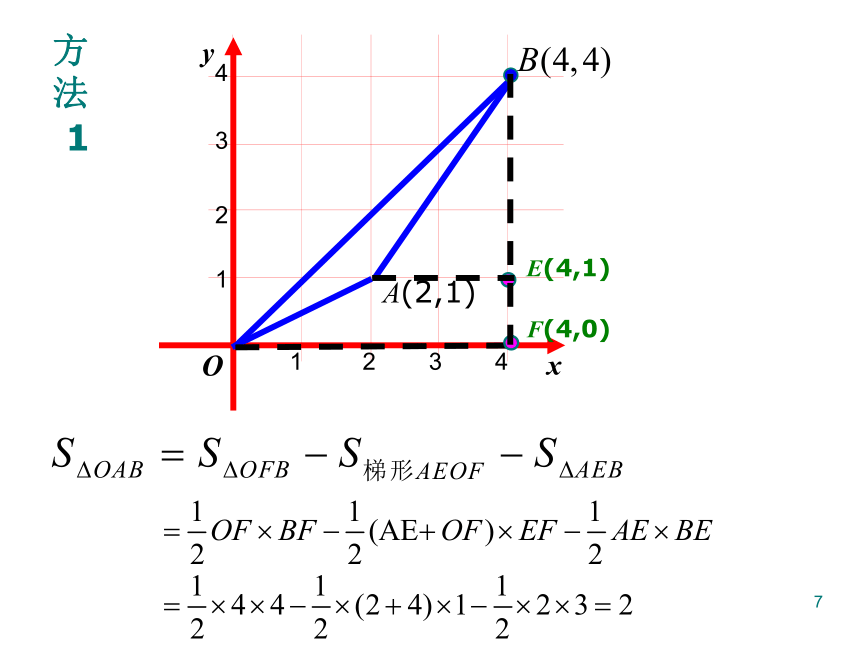
方
法
1
*
O
y
4
3
2
1
1 2 3 4
A(2,1)
x
E(2,0)
F(4,0)
方
法
2
*
O
y
4
3
2
1
1 2 3 4
A(2,1)
x
F(4,0)
方
法
3
*
已知△ABC中,A(-1,-2),B(6,2),C(1,3),求△ABC的面积。
y
-3
6
x
3
1
4
2
5
-2
-1
O
1
2
3
4
5
-2
-1
6
7
8
A(-1,-2)
B(6,2)
C(1,3)
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
D(6,-2)
E(6,3)
F(-1,3)
方法1
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
D(6,-2)
E(6,3)
方法2
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
E(6,3)
F(-1,3)
方法3
*
割补法求面积
谈谈我们的收获
化复杂为简单
转化思想
2、今天我们学习了什么数学思想?
1、在平面直角坐标系下,计算图形的面积可以运用什么方法?
平移
*
*
平面直角坐标系下图形 面积的计算
*
小结:
1. 已知P(a,b), 则点P到X轴的距离是 , 到Y轴的距离是 。
2. 若A(a,0),B(b,0) ,则AB= ;
若A(0,a),B(0,b) ,则AB= 。
3. 若A(a,c),B(b,c) ,则AB= ;
若A(c,a),B(c,b) ,则AB= 。
已知胡清菁同学的坐标是A(-1,0),郑义科同学的坐标是B(0,3),你能找到自己的坐标吗?
*
(1)已知A(-1,0),B(0,3),C(-4,0),
求△ABC的面积。
*
(2)已知A(-1,0),B(3,0),C(2,-3),
求△ABC的面积。
小结:求△ABC的面积关键是确 定底和高。
*
(3)已知A(2,0),B(0,3),C(4,2),
求△ABC的面积。
*
O
y
4
3
2
1
1 2 3 4
A(2,1)
x
已知△ABC中,0(0,0),A(2,1),B(4,4),求△ABC的面积.
*
O
y
4
3
2
1
1 2 3 4
A(2,1)
x
E(4,1)
F(4,0)
方
法
1
*
O
y
4
3
2
1
1 2 3 4
A(2,1)
x
E(2,0)
F(4,0)
方
法
2
*
O
y
4
3
2
1
1 2 3 4
A(2,1)
x
F(4,0)
方
法
3
*
已知△ABC中,A(-1,-2),B(6,2),C(1,3),求△ABC的面积。
y
-3
6
x
3
1
4
2
5
-2
-1
O
1
2
3
4
5
-2
-1
6
7
8
A(-1,-2)
B(6,2)
C(1,3)
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
D(6,-2)
E(6,3)
F(-1,3)
方法1
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
D(6,-2)
E(6,3)
方法2
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
E(6,3)
F(-1,3)
方法3
*
割补法求面积
谈谈我们的收获
化复杂为简单
转化思想
2、今天我们学习了什么数学思想?
1、在平面直角坐标系下,计算图形的面积可以运用什么方法?
平移
*
