第4章 几何图形初步 章末复习(含答案)
图片预览

文档简介
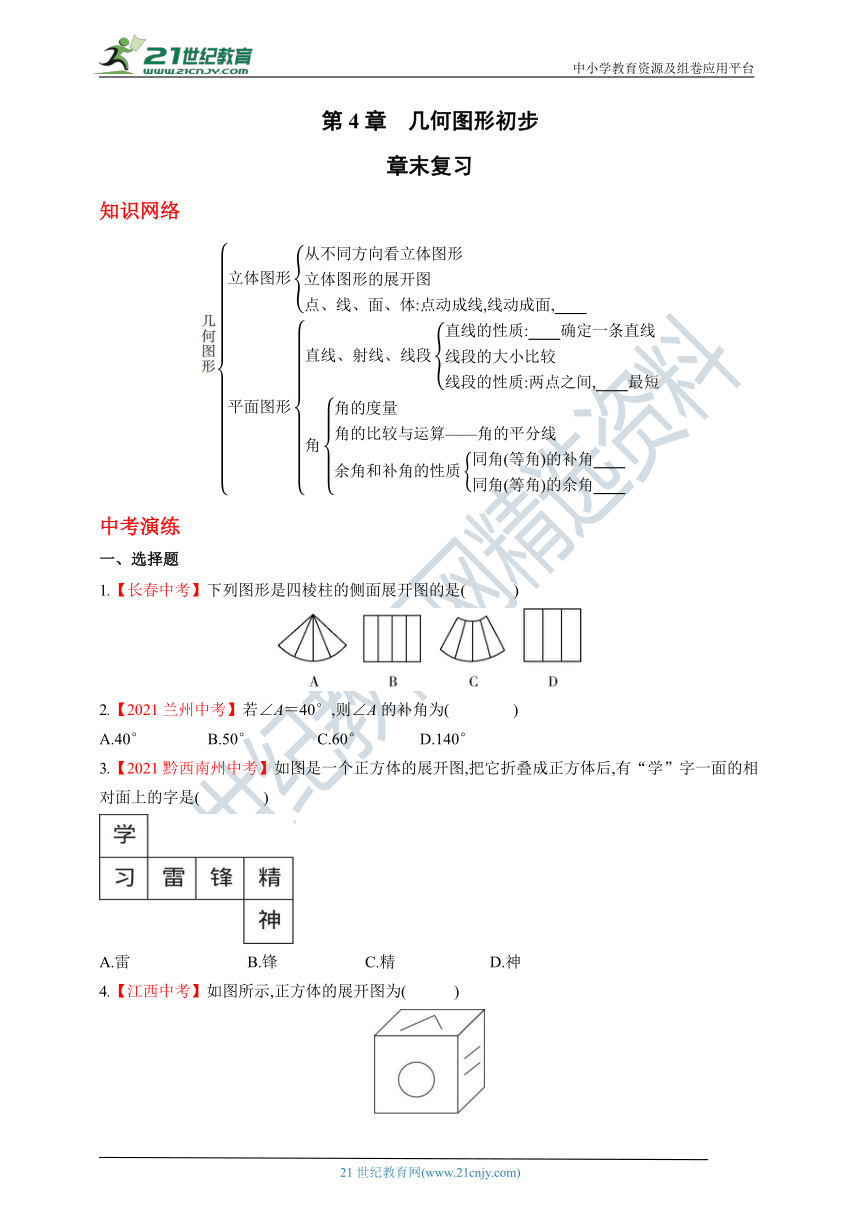
第4章 几何图形初步
章末复习
知识网络
中考演练
一、选择题
1.【长春中考】下列图形是四棱柱的侧面展开图的是( )
2.【2021兰州中考】若∠A=40°,则∠A的补角为( )
A.40° B.50° C.60° D.140°
3.【2021黔西南州中考】如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
4.【江西中考】如图所示,正方体的展开图为( )
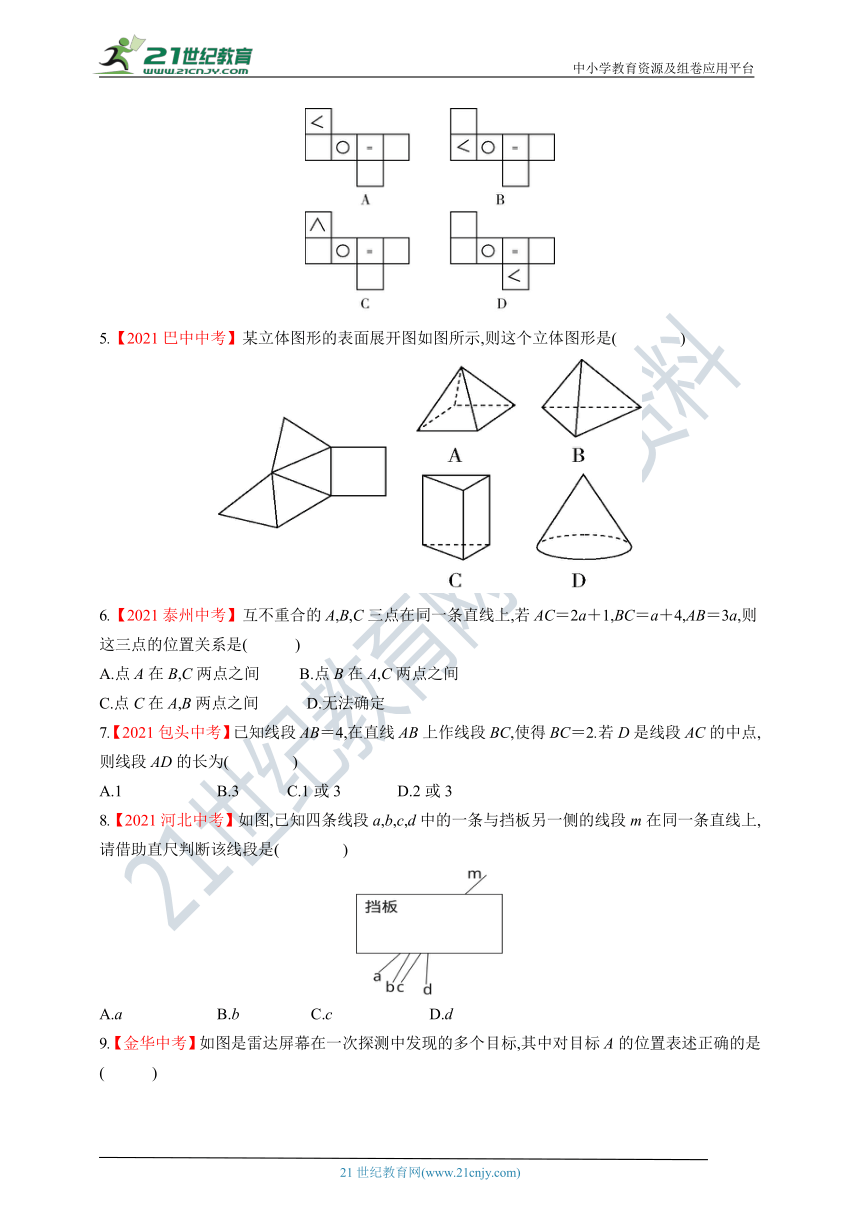
5.【2021巴中中考】某立体图形的表面展开图如图所示,则这个立体图形是( )
6.【2021泰州中考】互不重合的A,B,C三点在同一条直线上,若AC=2a+1,BC=a+4,AB=3a,则这三点的位置关系是( )
A.点A在B,C两点之间 B.点B在A,C两点之间
C.点C在A,B两点之间 D.无法确定
7.【2021包头中考】已知线段AB=4,在直线AB上作线段BC,使得BC=2.若D是线段AC的中点,则线段AD的长为( )
A.1 B.3 C.1或3 D.2或3
8.【2021河北中考】如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一条直线上,请借助直尺判断该线段是( )
A.a B.b C.c D.d
9.【金华中考】如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是( )
A.在南偏东75°方向处 B.在5 km处
C.在南偏东15°方向5 km处 D.在南偏东75°方向5 km处
二、填空题
10.【2021上海中考】70°的余角是 .
11.【2021兴安盟中考】74°19'30″= °.
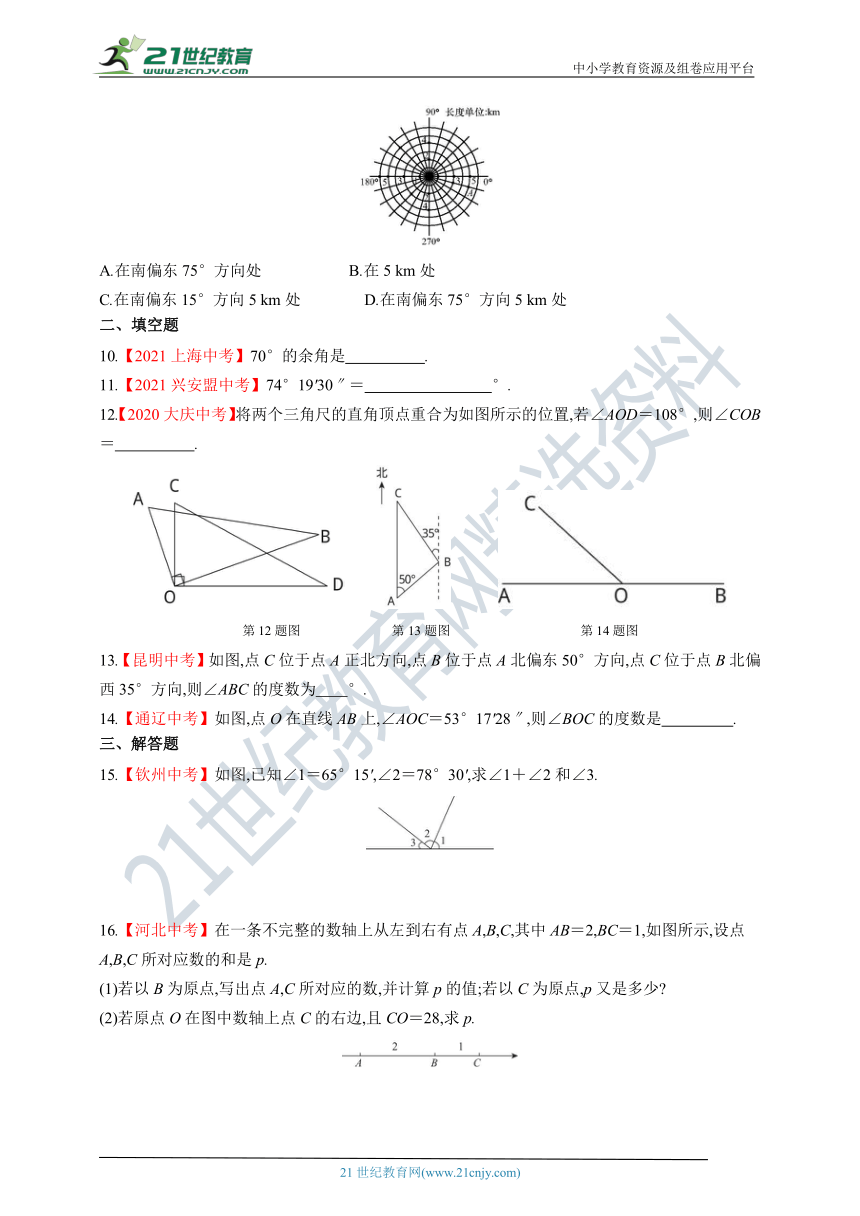
12.【2020大庆中考】将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB= .
第12题图 第13题图 第14题图
13.【昆明中考】如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 °.
14.【通辽中考】如图,点O在直线AB上,∠AOC=53°17'28″,则∠BOC的度数是 .
三、解答题
15.【钦州中考】如图,已知∠1=65°15',∠2=78°30',求∠1+∠2和∠3.
16.【河北中考】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
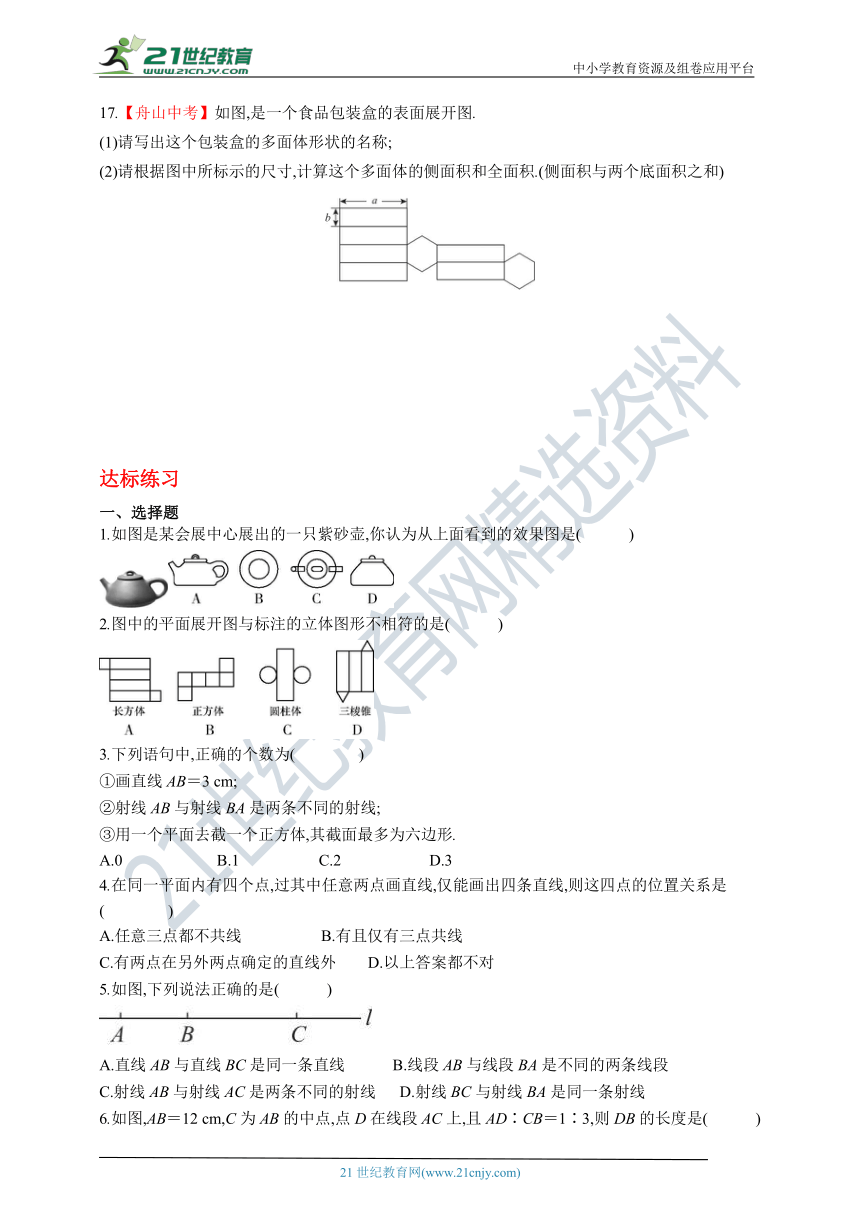
17.【舟山中考】如图,是一个食品包装盒的表面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标示的尺寸,计算这个多面体的侧面积和全面积.(侧面积与两个底面积之和)
达标练习
一、选择题
1.如图是某会展中心展出的一只紫砂壶,你认为从上面看到的效果图是( )
2.图中的平面展开图与标注的立体图形不相符的是( )
3.下列语句中,正确的个数为( )
①画直线AB=3 cm;
②射线AB与射线BA是两条不同的射线;
③用一个平面去截一个正方体,其截面最多为六边形.
A.0 B.1 C.2 D.3
4.在同一平面内有四个点,过其中任意两点画直线,仅能画出四条直线,则这四点的位置关系是( )
A.任意三点都不共线 B.有且仅有三点共线
C.有两点在另外两点确定的直线外 D.以上答案都不对
5.如图,下列说法正确的是( )
A.直线AB与直线BC是同一条直线 B.线段AB与线段BA是不同的两条线段
C.射线AB与射线AC是两条不同的射线 D.射线BC与射线BA是同一条射线
6.如图,AB=12 cm,C为AB的中点,点D在线段AC上,且AD∶CB=1∶3,则DB的长度是( )
A.4 cm B.6 cm C.8 cm D.10 cm
7.永州境内的潇水河畔有朝阳岩、柳子庙和迴龙塔等三个名胜古迹(如图所示),其中柳子庙坐落在潇水之西的柳子街上,始建于1056年,是永州人民为纪念唐宋八大家之一的柳宗元而筑建.现有三位游客分别参观这三个景点,为了使这三位游客参观完景点后步行返回旅游车上所走的路程总和最短,那么旅游车等候这三位游客的最佳地点应在( )
A.朝阳岩 B.柳子庙 C.迴龙塔 D.朝阳岩和迴龙塔这段路程的中间位置
8.如图,下列说法不正确的是( )
A.直线m,n相交于点P B.直线m不经过点Q C.PA+PB<QA+QB D.直线m上共有三个点
二、填空题
9.如果圆柱的侧面展开图是相邻两边长分别为5和4π的长方形,那么圆柱的体积是 .
10.某食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:
碟子的个数 碟子的高度/cm
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
现在分别从三个方向上看若干碟子,得到的图形如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度为 cm.
11.直线AB,BC,CA的位置关系如图所示,则下列语句:
①点B在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④B是直线AB,BC的交点.其中正确语句的有 .(只填写序号)
第11题图 第12题图
12.如图所示.
(1)图中经过点D的直线有 条,它们是 .
(2)图中以A为端点的射线有 条,它们是 .
13.已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任意三点在同一直线上.设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn= .
三、解答题
14.如图,已知某长方体的展开图的面积为310 cm2,求x的值.
15.已知线段AB,延长AB到点C,使AB=BC,反向延长AB到点D,使AD=4AB,E是线段CD的中点.若DE=12 cm,求:
(1)线段AB的长;
(2)线段AE的长.
16.已知点B在线段AC上,点D在线段AB上,
(1)如图1,若AB=6 cm,BC=4 cm,D为线段AC的中点,求线段DB的长度;
(2)如图2,若BD=AB=CD,E为线段AB的中点,EC=12 cm,求线段AC的长度.
17.如图,OC表示北偏东54°方向,OD平分∠BOC.
(1)求∠BOD的度数;
(2)请正确描述射线OD表示的方向.
18.如图,已知∠AOB=40°.
(1)如图1,若∠AOC=∠BOC,则∠BOC= ;
(2)如图2,∠AOC=30°,OM为∠AOB内部的一条射线,ON是∠MOC内部的一条射线,且3∠CON=∠NOM.求4∠AON+∠COM.
图1 图2
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
知识网络
中考演练
一、选择题
1.【长春中考】下列图形是四棱柱的侧面展开图的是( B )
2.【2021兰州中考】若∠A=40°,则∠A的补角为( D )
A.40° B.50° C.60° D.140°
3.【2021黔西南州中考】如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( D )
A.雷 B.锋 C.精 D.神
4.【江西中考】如图所示,正方体的展开图为( A )
5.【2021巴中中考】某立体图形的表面展开图如图所示,则这个立体图形是( A )
6.【2021泰州中考】互不重合的A,B,C三点在同一条直线上,若AC=2a+1,BC=a+4,AB=3a,则这三点的位置关系是( A )
A.点A在B,C两点之间 B.点B在A,C两点之间
C.点C在A,B两点之间 D.无法确定
7.【2021包头中考】已知线段AB=4,在直线AB上作线段BC,使得BC=2.若D是线段AC的中点,则线段AD的长为( C )
A.1 B.3 C.1或3 D.2或3
8.【2021河北中考】如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一条直线上,请借助直尺判断该线段是( A )
A.a B.b C.c D.d
9.【金华中考】如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是( D )
A.在南偏东75°方向处 B.在5 km处
C.在南偏东15°方向5 km处 D.在南偏东75°方向5 km处
二、填空题
10.【2021上海中考】70°的余角是 .
【答案】20°
11.【2021兴安盟中考】74°19'30″= °.
【答案】74.325
12.【2020大庆中考】将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB= .
【答案】72°
第12题图 第13题图 第14题图
13.【昆明中考】如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 95 °.
14.【通辽中考】如图,点O在直线AB上,∠AOC=53°17'28″,则∠BOC的度数是 126°42'32″ .
三、解答题
15.【钦州中考】如图,已知∠1=65°15',∠2=78°30',求∠1+∠2和∠3.
解:因为∠1=65°15',∠2=78°30',
所以∠1+∠2=65°15'+78°30'=143°45',
所以∠3=180°-(∠1+∠2)=180°-143°45'=36°15'.
16.【河北中考】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
解:(1)若以B为原点,则点C表示1,点A表示-2,所以p=1+0-2=-1;
若以C为原点,则点A表示-3,点B表示-1,
所以p=-3-1+0=-4.
(2)若原点O在图中数轴上点C的右边,且CO=28,则点C表示-28,点B表示-29,点A表示-31,所以p=-31-29-28=-88.
17.【舟山中考】如图,是一个食品包装盒的表面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标示的尺寸,计算这个多面体的侧面积和全面积.(侧面积与两个底面积之和)
解:(1)根据图示可知形状为直六棱柱.
(2)由题可知S侧=6ab,S正六边形=b 2,
所以S全=S侧+2S正六边形=6ab+3 b 2.
达标练习
一、选择题
1.如图是某会展中心展出的一只紫砂壶,你认为从上面看到的效果图是( C )
2.图中的平面展开图与标注的立体图形不相符的是( D )
3.下列语句中,正确的个数为( C )
①画直线AB=3 cm;
②射线AB与射线BA是两条不同的射线;
③用一个平面去截一个正方体,其截面最多为六边形.
A.0 B.1 C.2 D.3
4.在同一平面内有四个点,过其中任意两点画直线,仅能画出四条直线,则这四点的位置关系是( B )
A.任意三点都不共线 B.有且仅有三点共线
C.有两点在另外两点确定的直线外 D.以上答案都不对
5.如图,下列说法正确的是( A )
A.直线AB与直线BC是同一条直线 B.线段AB与线段BA是不同的两条线段
C.射线AB与射线AC是两条不同的射线 D.射线BC与射线BA是同一条射线
6.如图,AB=12 cm,C为AB的中点,点D在线段AC上,且AD∶CB=1∶3,则DB的长度是( D )
A.4 cm B.6 cm C.8 cm D.10 cm
7.永州境内的潇水河畔有朝阳岩、柳子庙和迴龙塔等三个名胜古迹(如图所示),其中柳子庙坐落在潇水之西的柳子街上,始建于1056年,是永州人民为纪念唐宋八大家之一的柳宗元而筑建.现有三位游客分别参观这三个景点,为了使这三位游客参观完景点后步行返回旅游车上所走的路程总和最短,那么旅游车等候这三位游客的最佳地点应在( B )
A.朝阳岩 B.柳子庙 C.迴龙塔 D.朝阳岩和迴龙塔这段路程的中间位置
8.如图,下列说法不正确的是( D )
A.直线m,n相交于点P B.直线m不经过点Q C.PA+PB<QA+QB D.直线m上共有三个点
二、填空题
9.如果圆柱的侧面展开图是相邻两边长分别为5和4π的长方形,那么圆柱的体积是 20π或25 .
10.某食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:
碟子的个数 碟子的高度/cm
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
现在分别从三个方向上看若干碟子,得到的图形如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度为 23 cm.
11.直线AB,BC,CA的位置关系如图所示,则下列语句:
①点B在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④B是直线AB,BC的交点.其中正确语句的有 ①③④ .(只填写序号)
第11题图 第12题图
12.如图所示.
(1)图中经过点D的直线有 3 条,它们是 直线AD,BC,DE .
(2)图中以A为端点的射线有 4 条,它们是 射线AB,AD,AE,AF .
13.已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任意三点在同一直线上.设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn= .
三、解答题
14.如图,已知某长方体的展开图的面积为310 cm2,求x的值.
解:由题意得2×(10x+5x+5×10)=310,
解得x=7.
15.已知线段AB,延长AB到点C,使AB=BC,反向延长AB到点D,使AD=4AB,E是线段CD的中点.若DE=12 cm,求:
(1)线段AB的长;
(2)线段AE的长.
解:画图如下.
(1)因为E是线段CD的中点,DE=12 cm,
所以CD=2DE=24 cm.
因为AB=BC,AD=4AB,
所以CD=AD+AB+BC=4AB+AB+AB=6AB,
所以6AB=24 cm,所以AB=4 cm.
(2)因为AB=4 cm,所以AD=4AB=16 cm,
所以AE=AD-DE=4 cm.
16.已知点B在线段AC上,点D在线段AB上,
(1)如图1,若AB=6 cm,BC=4 cm,D为线段AC的中点,求线段DB的长度;
(2)如图2,若BD=AB=CD,E为线段AB的中点,EC=12 cm,求线段AC的长度.
解:(1)因为AC=AB+BC,AB=6 cm,BC=4 cm,
所以AC=10 cm.
又因为D为线段AC的中点,
所以DC=AC=5 cm,
所以DB=DC-BC=1 cm.
(2)设BD=x cm,则AB=4x cm,CD=3x cm.
因为DC=DB+BC,所以BC=2x.
又因为AC=AB+BC,所以AC=6x cm.
因为E为线段AB的中点,所以BE=AB=2x cm.
因为EC=BE+BC,所以EC=2x+2x=4x cm,
所以4x=12,解得x=3,所以AC=6x=18 cm.
17.如图,OC表示北偏东54°方向,OD平分∠BOC.
(1)求∠BOD的度数;
(2)请正确描述射线OD表示的方向.
解:(1)因为∠1=54°,所以∠BOC=90°+∠1=144°.
因为OD平分∠BOC,所以∠BOD=∠BOC=72°.
(2)因为∠DOE=90°-∠BOD=90°-72°=18°,
所以射线OD表示北偏西18°方向.
18.如图,已知∠AOB=40°.
(1)如图1,若∠AOC=∠BOC,则∠BOC= ;
【答案】30°或60°
(2)如图2,∠AOC=30°,OM为∠AOB内部的一条射线,ON是∠MOC内部的一条射线,且3∠CON=∠NOM.求4∠AON+∠COM.
图1 图2
解:(2)设∠CON=α,则∠NOM=3∠CON=3α.
所以∠COM=4α.
因为∠AOC=30°,
所以∠AON=∠AOC-∠CON=30°-α,
所以4∠AON+∠COM=4(30°-α)+4α=120°.
.
章末复习
知识网络
中考演练
一、选择题
1.【长春中考】下列图形是四棱柱的侧面展开图的是( )
2.【2021兰州中考】若∠A=40°,则∠A的补角为( )
A.40° B.50° C.60° D.140°
3.【2021黔西南州中考】如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
4.【江西中考】如图所示,正方体的展开图为( )
5.【2021巴中中考】某立体图形的表面展开图如图所示,则这个立体图形是( )
6.【2021泰州中考】互不重合的A,B,C三点在同一条直线上,若AC=2a+1,BC=a+4,AB=3a,则这三点的位置关系是( )
A.点A在B,C两点之间 B.点B在A,C两点之间
C.点C在A,B两点之间 D.无法确定
7.【2021包头中考】已知线段AB=4,在直线AB上作线段BC,使得BC=2.若D是线段AC的中点,则线段AD的长为( )
A.1 B.3 C.1或3 D.2或3
8.【2021河北中考】如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一条直线上,请借助直尺判断该线段是( )
A.a B.b C.c D.d
9.【金华中考】如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是( )
A.在南偏东75°方向处 B.在5 km处
C.在南偏东15°方向5 km处 D.在南偏东75°方向5 km处
二、填空题
10.【2021上海中考】70°的余角是 .
11.【2021兴安盟中考】74°19'30″= °.
12.【2020大庆中考】将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB= .
第12题图 第13题图 第14题图
13.【昆明中考】如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 °.
14.【通辽中考】如图,点O在直线AB上,∠AOC=53°17'28″,则∠BOC的度数是 .
三、解答题
15.【钦州中考】如图,已知∠1=65°15',∠2=78°30',求∠1+∠2和∠3.
16.【河北中考】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
17.【舟山中考】如图,是一个食品包装盒的表面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标示的尺寸,计算这个多面体的侧面积和全面积.(侧面积与两个底面积之和)
达标练习
一、选择题
1.如图是某会展中心展出的一只紫砂壶,你认为从上面看到的效果图是( )
2.图中的平面展开图与标注的立体图形不相符的是( )
3.下列语句中,正确的个数为( )
①画直线AB=3 cm;
②射线AB与射线BA是两条不同的射线;
③用一个平面去截一个正方体,其截面最多为六边形.
A.0 B.1 C.2 D.3
4.在同一平面内有四个点,过其中任意两点画直线,仅能画出四条直线,则这四点的位置关系是( )
A.任意三点都不共线 B.有且仅有三点共线
C.有两点在另外两点确定的直线外 D.以上答案都不对
5.如图,下列说法正确的是( )
A.直线AB与直线BC是同一条直线 B.线段AB与线段BA是不同的两条线段
C.射线AB与射线AC是两条不同的射线 D.射线BC与射线BA是同一条射线
6.如图,AB=12 cm,C为AB的中点,点D在线段AC上,且AD∶CB=1∶3,则DB的长度是( )
A.4 cm B.6 cm C.8 cm D.10 cm
7.永州境内的潇水河畔有朝阳岩、柳子庙和迴龙塔等三个名胜古迹(如图所示),其中柳子庙坐落在潇水之西的柳子街上,始建于1056年,是永州人民为纪念唐宋八大家之一的柳宗元而筑建.现有三位游客分别参观这三个景点,为了使这三位游客参观完景点后步行返回旅游车上所走的路程总和最短,那么旅游车等候这三位游客的最佳地点应在( )
A.朝阳岩 B.柳子庙 C.迴龙塔 D.朝阳岩和迴龙塔这段路程的中间位置
8.如图,下列说法不正确的是( )
A.直线m,n相交于点P B.直线m不经过点Q C.PA+PB<QA+QB D.直线m上共有三个点
二、填空题
9.如果圆柱的侧面展开图是相邻两边长分别为5和4π的长方形,那么圆柱的体积是 .
10.某食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:
碟子的个数 碟子的高度/cm
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
现在分别从三个方向上看若干碟子,得到的图形如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度为 cm.
11.直线AB,BC,CA的位置关系如图所示,则下列语句:
①点B在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④B是直线AB,BC的交点.其中正确语句的有 .(只填写序号)
第11题图 第12题图
12.如图所示.
(1)图中经过点D的直线有 条,它们是 .
(2)图中以A为端点的射线有 条,它们是 .
13.已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任意三点在同一直线上.设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn= .
三、解答题
14.如图,已知某长方体的展开图的面积为310 cm2,求x的值.
15.已知线段AB,延长AB到点C,使AB=BC,反向延长AB到点D,使AD=4AB,E是线段CD的中点.若DE=12 cm,求:
(1)线段AB的长;
(2)线段AE的长.
16.已知点B在线段AC上,点D在线段AB上,
(1)如图1,若AB=6 cm,BC=4 cm,D为线段AC的中点,求线段DB的长度;
(2)如图2,若BD=AB=CD,E为线段AB的中点,EC=12 cm,求线段AC的长度.
17.如图,OC表示北偏东54°方向,OD平分∠BOC.
(1)求∠BOD的度数;
(2)请正确描述射线OD表示的方向.
18.如图,已知∠AOB=40°.
(1)如图1,若∠AOC=∠BOC,则∠BOC= ;
(2)如图2,∠AOC=30°,OM为∠AOB内部的一条射线,ON是∠MOC内部的一条射线,且3∠CON=∠NOM.求4∠AON+∠COM.
图1 图2
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
知识网络
中考演练
一、选择题
1.【长春中考】下列图形是四棱柱的侧面展开图的是( B )
2.【2021兰州中考】若∠A=40°,则∠A的补角为( D )
A.40° B.50° C.60° D.140°
3.【2021黔西南州中考】如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( D )
A.雷 B.锋 C.精 D.神
4.【江西中考】如图所示,正方体的展开图为( A )
5.【2021巴中中考】某立体图形的表面展开图如图所示,则这个立体图形是( A )
6.【2021泰州中考】互不重合的A,B,C三点在同一条直线上,若AC=2a+1,BC=a+4,AB=3a,则这三点的位置关系是( A )
A.点A在B,C两点之间 B.点B在A,C两点之间
C.点C在A,B两点之间 D.无法确定
7.【2021包头中考】已知线段AB=4,在直线AB上作线段BC,使得BC=2.若D是线段AC的中点,则线段AD的长为( C )
A.1 B.3 C.1或3 D.2或3
8.【2021河北中考】如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一条直线上,请借助直尺判断该线段是( A )
A.a B.b C.c D.d
9.【金华中考】如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是( D )
A.在南偏东75°方向处 B.在5 km处
C.在南偏东15°方向5 km处 D.在南偏东75°方向5 km处
二、填空题
10.【2021上海中考】70°的余角是 .
【答案】20°
11.【2021兴安盟中考】74°19'30″= °.
【答案】74.325
12.【2020大庆中考】将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB= .
【答案】72°
第12题图 第13题图 第14题图
13.【昆明中考】如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 95 °.
14.【通辽中考】如图,点O在直线AB上,∠AOC=53°17'28″,则∠BOC的度数是 126°42'32″ .
三、解答题
15.【钦州中考】如图,已知∠1=65°15',∠2=78°30',求∠1+∠2和∠3.
解:因为∠1=65°15',∠2=78°30',
所以∠1+∠2=65°15'+78°30'=143°45',
所以∠3=180°-(∠1+∠2)=180°-143°45'=36°15'.
16.【河北中考】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
解:(1)若以B为原点,则点C表示1,点A表示-2,所以p=1+0-2=-1;
若以C为原点,则点A表示-3,点B表示-1,
所以p=-3-1+0=-4.
(2)若原点O在图中数轴上点C的右边,且CO=28,则点C表示-28,点B表示-29,点A表示-31,所以p=-31-29-28=-88.
17.【舟山中考】如图,是一个食品包装盒的表面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标示的尺寸,计算这个多面体的侧面积和全面积.(侧面积与两个底面积之和)
解:(1)根据图示可知形状为直六棱柱.
(2)由题可知S侧=6ab,S正六边形=b 2,
所以S全=S侧+2S正六边形=6ab+3 b 2.
达标练习
一、选择题
1.如图是某会展中心展出的一只紫砂壶,你认为从上面看到的效果图是( C )
2.图中的平面展开图与标注的立体图形不相符的是( D )
3.下列语句中,正确的个数为( C )
①画直线AB=3 cm;
②射线AB与射线BA是两条不同的射线;
③用一个平面去截一个正方体,其截面最多为六边形.
A.0 B.1 C.2 D.3
4.在同一平面内有四个点,过其中任意两点画直线,仅能画出四条直线,则这四点的位置关系是( B )
A.任意三点都不共线 B.有且仅有三点共线
C.有两点在另外两点确定的直线外 D.以上答案都不对
5.如图,下列说法正确的是( A )
A.直线AB与直线BC是同一条直线 B.线段AB与线段BA是不同的两条线段
C.射线AB与射线AC是两条不同的射线 D.射线BC与射线BA是同一条射线
6.如图,AB=12 cm,C为AB的中点,点D在线段AC上,且AD∶CB=1∶3,则DB的长度是( D )
A.4 cm B.6 cm C.8 cm D.10 cm
7.永州境内的潇水河畔有朝阳岩、柳子庙和迴龙塔等三个名胜古迹(如图所示),其中柳子庙坐落在潇水之西的柳子街上,始建于1056年,是永州人民为纪念唐宋八大家之一的柳宗元而筑建.现有三位游客分别参观这三个景点,为了使这三位游客参观完景点后步行返回旅游车上所走的路程总和最短,那么旅游车等候这三位游客的最佳地点应在( B )
A.朝阳岩 B.柳子庙 C.迴龙塔 D.朝阳岩和迴龙塔这段路程的中间位置
8.如图,下列说法不正确的是( D )
A.直线m,n相交于点P B.直线m不经过点Q C.PA+PB<QA+QB D.直线m上共有三个点
二、填空题
9.如果圆柱的侧面展开图是相邻两边长分别为5和4π的长方形,那么圆柱的体积是 20π或25 .
10.某食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:
碟子的个数 碟子的高度/cm
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
现在分别从三个方向上看若干碟子,得到的图形如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度为 23 cm.
11.直线AB,BC,CA的位置关系如图所示,则下列语句:
①点B在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④B是直线AB,BC的交点.其中正确语句的有 ①③④ .(只填写序号)
第11题图 第12题图
12.如图所示.
(1)图中经过点D的直线有 3 条,它们是 直线AD,BC,DE .
(2)图中以A为端点的射线有 4 条,它们是 射线AB,AD,AE,AF .
13.已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任意三点在同一直线上.设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn= .
三、解答题
14.如图,已知某长方体的展开图的面积为310 cm2,求x的值.
解:由题意得2×(10x+5x+5×10)=310,
解得x=7.
15.已知线段AB,延长AB到点C,使AB=BC,反向延长AB到点D,使AD=4AB,E是线段CD的中点.若DE=12 cm,求:
(1)线段AB的长;
(2)线段AE的长.
解:画图如下.
(1)因为E是线段CD的中点,DE=12 cm,
所以CD=2DE=24 cm.
因为AB=BC,AD=4AB,
所以CD=AD+AB+BC=4AB+AB+AB=6AB,
所以6AB=24 cm,所以AB=4 cm.
(2)因为AB=4 cm,所以AD=4AB=16 cm,
所以AE=AD-DE=4 cm.
16.已知点B在线段AC上,点D在线段AB上,
(1)如图1,若AB=6 cm,BC=4 cm,D为线段AC的中点,求线段DB的长度;
(2)如图2,若BD=AB=CD,E为线段AB的中点,EC=12 cm,求线段AC的长度.
解:(1)因为AC=AB+BC,AB=6 cm,BC=4 cm,
所以AC=10 cm.
又因为D为线段AC的中点,
所以DC=AC=5 cm,
所以DB=DC-BC=1 cm.
(2)设BD=x cm,则AB=4x cm,CD=3x cm.
因为DC=DB+BC,所以BC=2x.
又因为AC=AB+BC,所以AC=6x cm.
因为E为线段AB的中点,所以BE=AB=2x cm.
因为EC=BE+BC,所以EC=2x+2x=4x cm,
所以4x=12,解得x=3,所以AC=6x=18 cm.
17.如图,OC表示北偏东54°方向,OD平分∠BOC.
(1)求∠BOD的度数;
(2)请正确描述射线OD表示的方向.
解:(1)因为∠1=54°,所以∠BOC=90°+∠1=144°.
因为OD平分∠BOC,所以∠BOD=∠BOC=72°.
(2)因为∠DOE=90°-∠BOD=90°-72°=18°,
所以射线OD表示北偏西18°方向.
18.如图,已知∠AOB=40°.
(1)如图1,若∠AOC=∠BOC,则∠BOC= ;
【答案】30°或60°
(2)如图2,∠AOC=30°,OM为∠AOB内部的一条射线,ON是∠MOC内部的一条射线,且3∠CON=∠NOM.求4∠AON+∠COM.
图1 图2
解:(2)设∠CON=α,则∠NOM=3∠CON=3α.
所以∠COM=4α.
因为∠AOC=30°,
所以∠AON=∠AOC-∠CON=30°-α,
所以4∠AON+∠COM=4(30°-α)+4α=120°.
.
