§:3.2.1几类不同增长的函数模型习题课[上学期]
文档属性
| 名称 | §:3.2.1几类不同增长的函数模型习题课[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 63.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-15 00:00:00 | ||
图片预览




文档简介
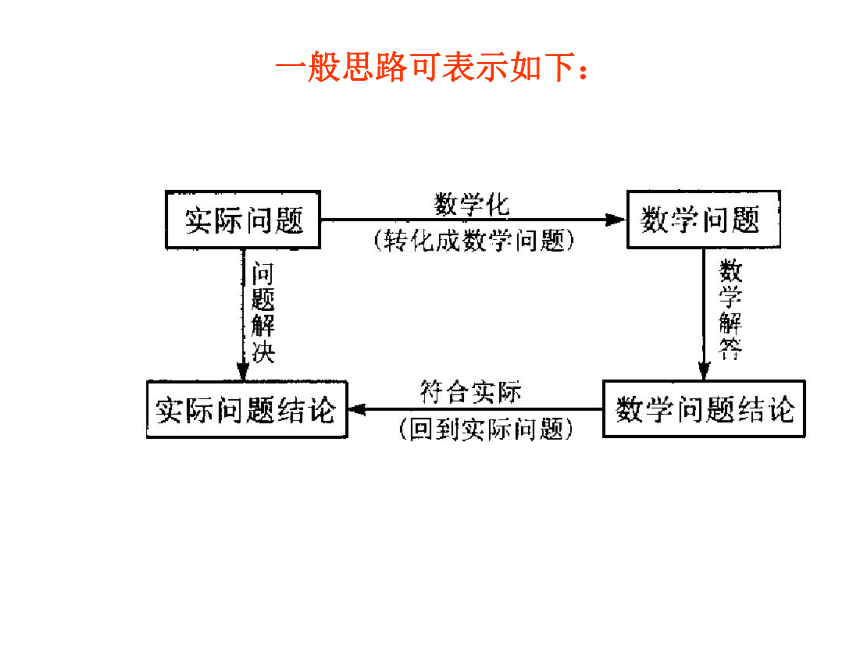
课件19张PPT。§:3.2.1几类不同增长的函数模型一般思路可表示如下: 解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
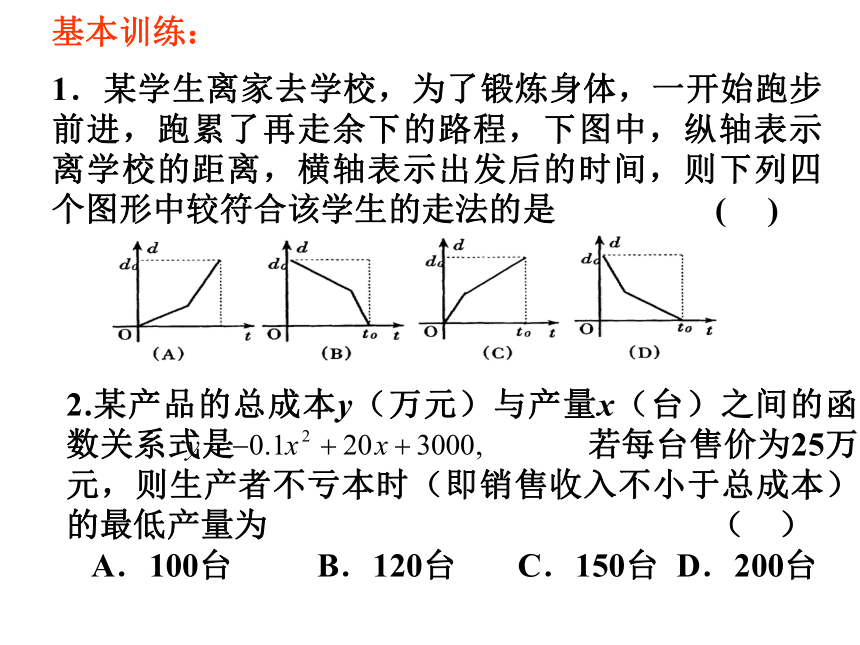
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义. 基本训练: 1.某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程,下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该学生的走法的是 ( ) 2.某产品的总成本y(万元)与产量x(台)之间的函数关系式是 若每台售价为25万元,则生产者不亏本时(即销售收入不小于总成本)的最低产量为 ( )
A.100台 B.120台 C.150台 D.200台
3.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3小时,这种细菌由1个可繁殖成 ( )
A. 511个 B. 512个 C. 1023个 D. 1024个
4.某工厂生产两种成本不同的产品,由于市场销售发生变化,A产品连续两次提价20%,B产品连续两次降价20%,结果都以23.04元出售,此时厂家同时出售A、B产品各一件,盈亏情况为 ( )
A.不亏不赚 B.亏5.92元C.赚5.92元 D.赚28.96元5.某企业近几年的年产值如图,则年增长率最高的是(增长率=增长值/原产值) ( )
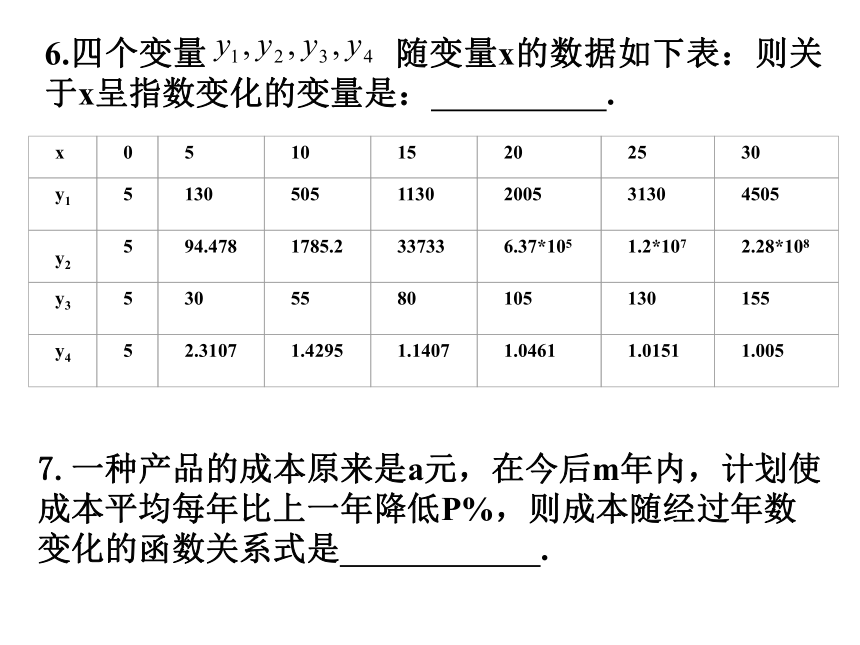
A)97年 B)98年 C)99年 D)00年6.四个变量 随变量x的数据如下表:则关于x呈指数变化的变量是: .7.一种产品的成本原来是a元,在今后m年内,计划使成本平均每年比上一年降低P%,则成本随经过年数变化的函数关系式是 . 8.据新华社2002年3月12日电,1985年到2000年间,我国农村人均居住面积如图2—1所示,其中从____年到_____年的五年间增长最快.图2—19、某商店出售茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,该商店制定了两种优惠办法:
(1)买一只茶壶赠送一只茶杯;
(2)按总价的92%付款.
某顾客需买茶壶4只,茶杯若干(不少于4只),若购买茶杯 (只)付款 (元),试分别建立两种优惠办法中 与 之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪种更省钱?10.一家人(父亲、母亲、孩子)去某地旅游,有两个旅行社同时发出邀请,且有各自的优惠政策.甲旅行社承诺,如果父亲买一张全票,则其家庭成员均可享受半价,乙旅行社承诺,家庭旅行算团体票,按原价的 计算,这两家旅行社的原价是一样的,若家庭中孩子数不同,试分别列出两家旅行社优惠政策实施后的孩子个数为变量的收费表达式,比较选择哪家更优惠? §3.2.1几类不同增长的函数模型(2) 基本训练: 1.某纯净水制造厂在净化水的过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需要过滤的次数为 ( )
(参考数据lg2=0.3010,lg3=0.4771)
A.5 B.10 C.14 D.15 2.向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系的图象如图2—4所示,那么水瓶的形状是 ( ) 图2—4
3.计算机的成本不断下降,若每隔5年计算机的价格降低现价格的 ,现在价格5400元的计算机经过15年的价格为_______.4.按国家统计局资料,到1989年初,我国大陆人口总数达到11亿,人口自然增长率约为14%,按此自然增长率计算,我国大陆人口达到13亿时是_________年初(填写年号),(用下面数据帮助计算:lg13=1.1139,lg11=1.0414,lg1.014=0.0060) 5.某城市出租汽车统一价格,凡上车起步价为6元,行程不超过2km者均按此价收费,行程超过2km,按1.8元/km收费,另外,遇到塞车或等候时,汽车虽没有行驶,仍按6分钟折算1km计算,陈先生坐了一趟这种出租车,车费17元,车上仪表显示等候时间为11分30秒,那么陈先生此趟行程介于( )
A.5~7 B.9~11km
C.7~9km D.3~5km 6.国际上常用恩格尔系数(记作n)来衡量一个国家和地区人民生活水平的状况,它的计算公式为:
n= ×100%,各种类型家庭的n如下表所示 根据某市城市家庭抽样调查统计,1997年至2003年间,每户家庭支出总额每年平均增加700元,其中食品消费支出总额每年平均增加100元.
(1)若1997年该市城区刚达到小康,且该年每户家庭消费支出总额为9000元,问2002年能否达到富裕?
(2)若2002年比1997年的消费支出总额增加35%,而其中食品消费支出总额增加10%,问哪一年能达到富裕? 7.某地方政府为保护地方电子工业发展,决定对某一进口电子产品征收附加税.已知这种电子产品国内市场零售价为每件250元,每年可销售40万件,若政府增加附加税率为每百元收 t元时,则每年销售量将减少t万件.
(1)将税金收入表示为征收附加税率的函数;
(2)若在该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围? 8.某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、1.2 万件、1.3 万件,为了估测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量 与月份的关系,模拟函数可以选用二次函数或函数 (其中 为常数)已知4月份该产品的产量为1.37万件, 请问用以上哪个函数作为模拟函数较好,并说明理由
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义. 基本训练: 1.某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程,下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该学生的走法的是 ( ) 2.某产品的总成本y(万元)与产量x(台)之间的函数关系式是 若每台售价为25万元,则生产者不亏本时(即销售收入不小于总成本)的最低产量为 ( )
A.100台 B.120台 C.150台 D.200台
3.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3小时,这种细菌由1个可繁殖成 ( )
A. 511个 B. 512个 C. 1023个 D. 1024个
4.某工厂生产两种成本不同的产品,由于市场销售发生变化,A产品连续两次提价20%,B产品连续两次降价20%,结果都以23.04元出售,此时厂家同时出售A、B产品各一件,盈亏情况为 ( )
A.不亏不赚 B.亏5.92元C.赚5.92元 D.赚28.96元5.某企业近几年的年产值如图,则年增长率最高的是(增长率=增长值/原产值) ( )
A)97年 B)98年 C)99年 D)00年6.四个变量 随变量x的数据如下表:则关于x呈指数变化的变量是: .7.一种产品的成本原来是a元,在今后m年内,计划使成本平均每年比上一年降低P%,则成本随经过年数变化的函数关系式是 . 8.据新华社2002年3月12日电,1985年到2000年间,我国农村人均居住面积如图2—1所示,其中从____年到_____年的五年间增长最快.图2—19、某商店出售茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,该商店制定了两种优惠办法:
(1)买一只茶壶赠送一只茶杯;
(2)按总价的92%付款.
某顾客需买茶壶4只,茶杯若干(不少于4只),若购买茶杯 (只)付款 (元),试分别建立两种优惠办法中 与 之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪种更省钱?10.一家人(父亲、母亲、孩子)去某地旅游,有两个旅行社同时发出邀请,且有各自的优惠政策.甲旅行社承诺,如果父亲买一张全票,则其家庭成员均可享受半价,乙旅行社承诺,家庭旅行算团体票,按原价的 计算,这两家旅行社的原价是一样的,若家庭中孩子数不同,试分别列出两家旅行社优惠政策实施后的孩子个数为变量的收费表达式,比较选择哪家更优惠? §3.2.1几类不同增长的函数模型(2) 基本训练: 1.某纯净水制造厂在净化水的过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需要过滤的次数为 ( )
(参考数据lg2=0.3010,lg3=0.4771)
A.5 B.10 C.14 D.15 2.向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系的图象如图2—4所示,那么水瓶的形状是 ( ) 图2—4
3.计算机的成本不断下降,若每隔5年计算机的价格降低现价格的 ,现在价格5400元的计算机经过15年的价格为_______.4.按国家统计局资料,到1989年初,我国大陆人口总数达到11亿,人口自然增长率约为14%,按此自然增长率计算,我国大陆人口达到13亿时是_________年初(填写年号),(用下面数据帮助计算:lg13=1.1139,lg11=1.0414,lg1.014=0.0060) 5.某城市出租汽车统一价格,凡上车起步价为6元,行程不超过2km者均按此价收费,行程超过2km,按1.8元/km收费,另外,遇到塞车或等候时,汽车虽没有行驶,仍按6分钟折算1km计算,陈先生坐了一趟这种出租车,车费17元,车上仪表显示等候时间为11分30秒,那么陈先生此趟行程介于( )
A.5~7 B.9~11km
C.7~9km D.3~5km 6.国际上常用恩格尔系数(记作n)来衡量一个国家和地区人民生活水平的状况,它的计算公式为:
n= ×100%,各种类型家庭的n如下表所示 根据某市城市家庭抽样调查统计,1997年至2003年间,每户家庭支出总额每年平均增加700元,其中食品消费支出总额每年平均增加100元.
(1)若1997年该市城区刚达到小康,且该年每户家庭消费支出总额为9000元,问2002年能否达到富裕?
(2)若2002年比1997年的消费支出总额增加35%,而其中食品消费支出总额增加10%,问哪一年能达到富裕? 7.某地方政府为保护地方电子工业发展,决定对某一进口电子产品征收附加税.已知这种电子产品国内市场零售价为每件250元,每年可销售40万件,若政府增加附加税率为每百元收 t元时,则每年销售量将减少t万件.
(1)将税金收入表示为征收附加税率的函数;
(2)若在该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围? 8.某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、1.2 万件、1.3 万件,为了估测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量 与月份的关系,模拟函数可以选用二次函数或函数 (其中 为常数)已知4月份该产品的产量为1.37万件, 请问用以上哪个函数作为模拟函数较好,并说明理由
