数学人教A版2019选修第二册5.2.1基本初等函数的导数 课件(共26张ppt)
文档属性
| 名称 | 数学人教A版2019选修第二册5.2.1基本初等函数的导数 课件(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 15:39:06 | ||
图片预览







文档简介
(共26张PPT)
第 5 章一元函数的导数及其应用
人教A版2019选修第一册
5.2.1基本初等函数的导数
学习目标
能根据定义求函数y=c,y=x,y=x2,的导数.
2.掌握基本初等函数的导数公式,并能进行简单的应用.
l
l
由导数的定义可知,一个函数的导数是唯一确定的.在必修第一册中我们学过基本初等函数,并且知道,很多复杂的函数都是通过对这些函数进行加、减、乘、除等运算得到的.因此自然想到,能否先求出基本初等函数的导数,然后研究出导数的“运算法则”,这样就可以利用导数的运算法则和基本初等函数的导数求出复杂函数的导数.本节我们就来研究这些问题.
根据导数的定义,求函数的导数,就是求出当时,无限趋近的那个定值.下面我们求几个常用函数的导数.
1. 函数y=f(x)=c的导数
即
若y=c (如图示)表示路程关于时间的函数,则y′=0可以解释为某物体的瞬时速度始终为0,即一 直处于静止状态.
也就是说任意一个常数的导数是0.
x
y
y=c
O
即
若y=x (如图示)表示路程关于时间的函数,则y′=1可以解释为某物体做瞬时速度为1的匀速直线运动.
x
y
y=x
O
2. 函数y=f(x)=x的导数
即
若y=x2表示路程关于时间的函数,则y′=2x可以解释为某物体做变速运动,它在时刻x的瞬时速度为2x.
3. 函数y=f(x)=x2的导数
y′= 2x表示函数y=x2的图象上点(x, y)处切线的斜率为2x, 说明随着x的变化, 切线的斜率也在变化.
y′= 2x表明: 当x<0时,随着x的增加,|y′|越来越小, y=x2减少得越来越慢;
当x>0时,随着x的增加,|y′|越来越大, y=x2增加得越来越快.
x
y
y=x2
O
即
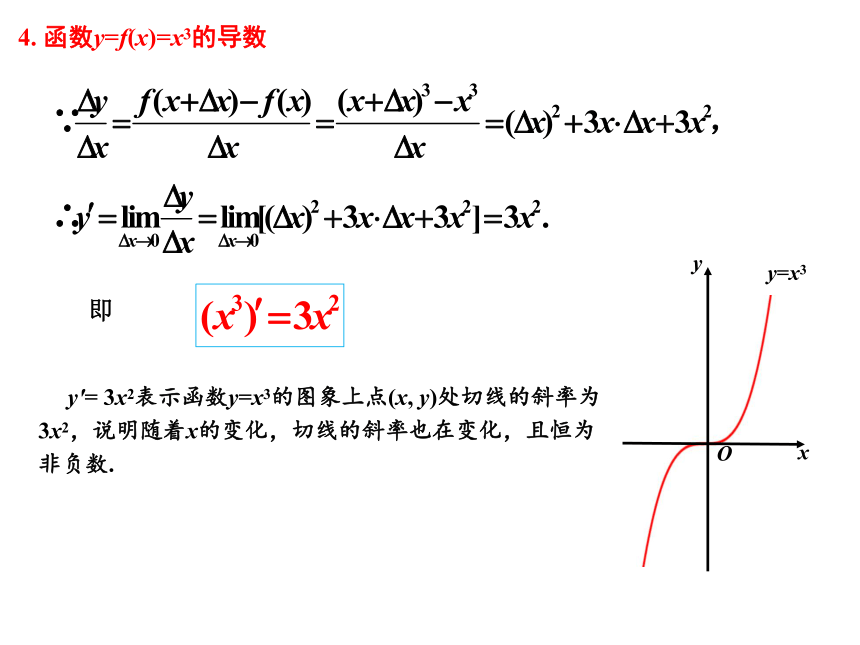
4. 函数y=f(x)=x3的导数
y′= 3x2表示函数y=x3的图象上点(x, y)处切线的斜率为3x2,说明随着x的变化,切线的斜率也在变化,且恒为非负数.
x
y
y=x3
O
即
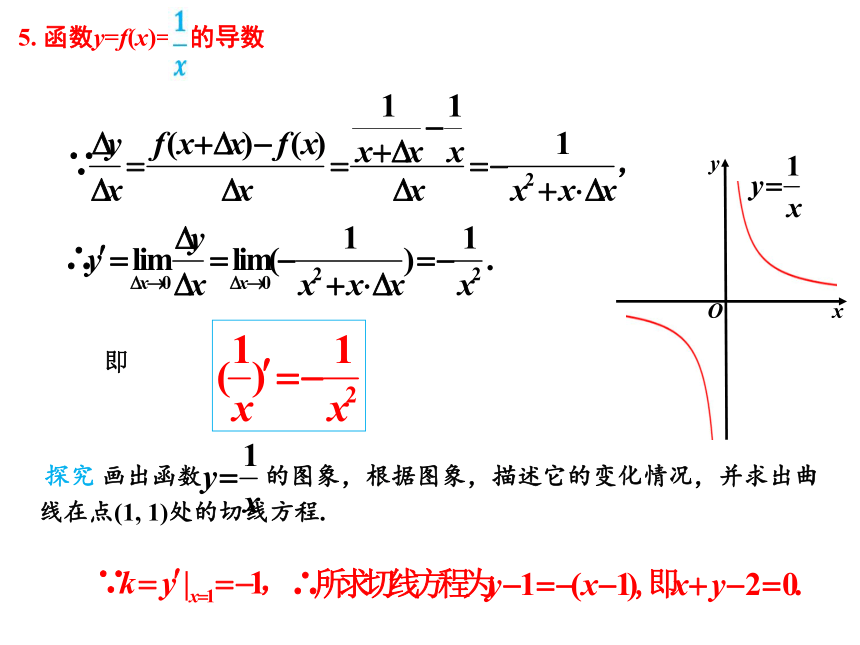
5. 函数y=f(x)= 的导数
探究 画出函数 的图象,根据图象,描述它的变化情况,并求出曲线在点(1, 1)处的切线方程.
x
y
O
即
6. 函数y=f(x)= 的导数
例1 求下列函数的导数:
解:
方法技巧:
求函数的导数的常见类型及解题技巧
(1)对于分式中分子、分母为齐次结构的函数,可考虑通过裂项为和差形式.
(2)对于根式型函数,可考虑进行有理化变形.
(3)对于多个整式乘积形式的函数,可考虑展开,化为和差形式.
(4)对于三角函数,可考虑恒等变形,使函数的种类减少,次数降低,结构尽量简单,从而便于求导.
例2 假设某地在20年间的年均通货膨胀率为5%,物价p(单位:元)与时间t(单位:年)之间的关系为 其中p0为t=0时的物价. 假定某种商品的p0=1,那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01元/年)
解:
课堂练习
1. 求下列函数的导数:
解:
1. 求下列函数的导数:
解:
2. 求下列函数在给定点处的导数:
解:
解:
解:
随堂检测
当堂达标
注意:利用导数公式求导时,应根据所给问题的特征,恰当地选择求导公式.有时还要先对函数解析式进行化简整理,这样能够简化运算过程.
课堂小结
第 5 章一元函数的导数及其应用
人教A版2019选修第一册
5.2.1基本初等函数的导数
学习目标
能根据定义求函数y=c,y=x,y=x2,的导数.
2.掌握基本初等函数的导数公式,并能进行简单的应用.
l
l
由导数的定义可知,一个函数的导数是唯一确定的.在必修第一册中我们学过基本初等函数,并且知道,很多复杂的函数都是通过对这些函数进行加、减、乘、除等运算得到的.因此自然想到,能否先求出基本初等函数的导数,然后研究出导数的“运算法则”,这样就可以利用导数的运算法则和基本初等函数的导数求出复杂函数的导数.本节我们就来研究这些问题.
根据导数的定义,求函数的导数,就是求出当时,无限趋近的那个定值.下面我们求几个常用函数的导数.
1. 函数y=f(x)=c的导数
即
若y=c (如图示)表示路程关于时间的函数,则y′=0可以解释为某物体的瞬时速度始终为0,即一 直处于静止状态.
也就是说任意一个常数的导数是0.
x
y
y=c
O
即
若y=x (如图示)表示路程关于时间的函数,则y′=1可以解释为某物体做瞬时速度为1的匀速直线运动.
x
y
y=x
O
2. 函数y=f(x)=x的导数
即
若y=x2表示路程关于时间的函数,则y′=2x可以解释为某物体做变速运动,它在时刻x的瞬时速度为2x.
3. 函数y=f(x)=x2的导数
y′= 2x表示函数y=x2的图象上点(x, y)处切线的斜率为2x, 说明随着x的变化, 切线的斜率也在变化.
y′= 2x表明: 当x<0时,随着x的增加,|y′|越来越小, y=x2减少得越来越慢;
当x>0时,随着x的增加,|y′|越来越大, y=x2增加得越来越快.
x
y
y=x2
O
即
4. 函数y=f(x)=x3的导数
y′= 3x2表示函数y=x3的图象上点(x, y)处切线的斜率为3x2,说明随着x的变化,切线的斜率也在变化,且恒为非负数.
x
y
y=x3
O
即
5. 函数y=f(x)= 的导数
探究 画出函数 的图象,根据图象,描述它的变化情况,并求出曲线在点(1, 1)处的切线方程.
x
y
O
即
6. 函数y=f(x)= 的导数
例1 求下列函数的导数:
解:
方法技巧:
求函数的导数的常见类型及解题技巧
(1)对于分式中分子、分母为齐次结构的函数,可考虑通过裂项为和差形式.
(2)对于根式型函数,可考虑进行有理化变形.
(3)对于多个整式乘积形式的函数,可考虑展开,化为和差形式.
(4)对于三角函数,可考虑恒等变形,使函数的种类减少,次数降低,结构尽量简单,从而便于求导.
例2 假设某地在20年间的年均通货膨胀率为5%,物价p(单位:元)与时间t(单位:年)之间的关系为 其中p0为t=0时的物价. 假定某种商品的p0=1,那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01元/年)
解:
课堂练习
1. 求下列函数的导数:
解:
1. 求下列函数的导数:
解:
2. 求下列函数在给定点处的导数:
解:
解:
解:
随堂检测
当堂达标
注意:利用导数公式求导时,应根据所给问题的特征,恰当地选择求导公式.有时还要先对函数解析式进行化简整理,这样能够简化运算过程.
课堂小结
