5.4.2 正弦函数、余弦函数的性质1周期性、奇偶性和对称性 课件(共22张PPT)
文档属性
| 名称 | 5.4.2 正弦函数、余弦函数的性质1周期性、奇偶性和对称性 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 15:39:48 | ||
图片预览








文档简介
正弦、余弦函数的性质
—周期性、奇偶性和对称性
新课教授
周期函数定义
?
定义:
?
T: 周期
?
?
????????=????(????+????)
?
作用:知道一个周期内的信息,就知道了整个定义域内的信息。
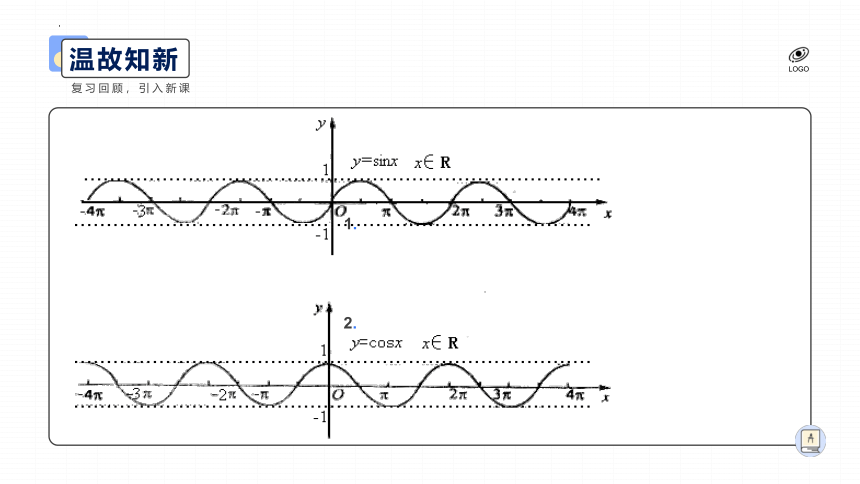
复习回顾,引入新课
温故知新
1.
2.
新课教授
最小正周期
?
?
????=sin????的最小正周期:
????=2????
?
知识点理解
理解周期函数的定义
小组讨论并完成下列判断题:
?
?
(2)周期函数的周期是唯一的.
理由:周期函数的周期不唯一
?
理由:周期函数不一定存在最小正周期.
周期求解常见题
计算周期
例1.
求下列函数的最小正周期:
1)????(????)=sin(????+????3)
?
2)????(????)=12cos(2????+????3)
?
3)????(????)=|sin????|
?
周期求解常见题
计算周期
例2.
求下列函数的最小正周期:
1)已知f(x)是定义在R上的函数,且f(x+4)=f(x-2),则f(x)的最小正周期为_____
2)已知f(x)是定义在R上的函数,且f(x+2)+f(x)=0,则f(x)的最小正周期为_____
4)已知f(x)是定义在R上的函数,且f(x+2)=1????(????),则f(x)的最小正周期为_____
?
5)已知f(x)是定义在R上的函数,且f(x+2).f(x)=13,则f(x)的最小正周期为_____
3)已知f(x)是定义在R上的函数,且f(x+2)+f(x)=3,则f(x)的最小正周期为_____
周期求解常见公式
总结
1.f(x+a)=f(x+b) T=|b-a|
2.f(x+a)=-f(x) T=2a
3.f(x+a)+f(x)=k(k为常数)T=2a
4.f(x+a)=1f(x) T=2a
5.f(x+a).f(x)=k(k为常数) T=2a
?
周期求解常见题
计算周期
2.若f(x)是奇函数,且f(x+1)=-f(x),当x∈(-1,0)时,f(x)=2x+1,求f(92)的值.
?
3.f(x)对任意实数x满足f(x+2)=1????(????), 若f(1)=5, 则f[f(5)]=
?
新课教学
正弦、余弦函数的奇偶性
????
?
?????2
?
?5????2
?
?3????
?
5????2
?
3????
?
问题:你能从它们的图象看出它们有何奇偶性吗?
正弦函数的图象
余弦函数的图象
2????
?
?2????
?
奇偶性
例题讲解
正弦函数奇偶性求值
1.已知f(x)=sin(2x+????),????∈[?????2,????2],且????(?????????6)为偶函数,则????=_____
?
2.已知函数f(x)=-sin(????????+????+????3),(??????
奇偶性
跟踪训练
(2).已知函数f(x)=sin(????+????4+????)是奇函数,则????∈[?????2,????2]时,????的值为____
?
新课教学
正弦函数的对称性
【思考】正弦函数、余弦函数的图象分别关于原点、y轴对称,除此以外它们是否还有其它的对称中心和对称轴呢?
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
新课教学
余弦函数的对称性
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
对称轴:直线x=kπ,k∈Z
对称性
例题讲解
例3???求函数????=cos(2?????????3)的对称轴方程和对称中心坐标.
?
对称性
例题讲解
练习:求下列函数的对称轴、对称中心:
(1)
(2)
对称性
例题讲解
对称性
例题讲解
3.(多选)关于函数f(x)=sin(2x+????3)(x∈R).下列命题正确的是( )
A. y=f(x)可以改写为y=4cos(2x-????6)
B. y=f(x)是以2????为最小正周期为周期函数
C. 函数y=f(x-????6)是奇函数
D. y=f(x+????12)的图像关于y轴对称·
?
对称性
例题讲解
奇偶性周期性的综合运用
奇偶性周期性的综合运用
3.已知函数f(x)是定义在R上的偶函数,且y=f(x)的图像关于直线x=2对称.
(1)证明:f(x)是周期函数
(2)若当x∈[-2,2]时,f(x)=-????2+1,当????∈[?6,?2]时,????(????)的解析式.
—周期性、奇偶性和对称性
新课教授
周期函数定义
?
定义:
?
T: 周期
?
?
????????=????(????+????)
?
作用:知道一个周期内的信息,就知道了整个定义域内的信息。
复习回顾,引入新课
温故知新
1.
2.
新课教授
最小正周期
?
?
????=sin????的最小正周期:
????=2????
?
知识点理解
理解周期函数的定义
小组讨论并完成下列判断题:
?
?
(2)周期函数的周期是唯一的.
理由:周期函数的周期不唯一
?
理由:周期函数不一定存在最小正周期.
周期求解常见题
计算周期
例1.
求下列函数的最小正周期:
1)????(????)=sin(????+????3)
?
2)????(????)=12cos(2????+????3)
?
3)????(????)=|sin????|
?
周期求解常见题
计算周期
例2.
求下列函数的最小正周期:
1)已知f(x)是定义在R上的函数,且f(x+4)=f(x-2),则f(x)的最小正周期为_____
2)已知f(x)是定义在R上的函数,且f(x+2)+f(x)=0,则f(x)的最小正周期为_____
4)已知f(x)是定义在R上的函数,且f(x+2)=1????(????),则f(x)的最小正周期为_____
?
5)已知f(x)是定义在R上的函数,且f(x+2).f(x)=13,则f(x)的最小正周期为_____
3)已知f(x)是定义在R上的函数,且f(x+2)+f(x)=3,则f(x)的最小正周期为_____
周期求解常见公式
总结
1.f(x+a)=f(x+b) T=|b-a|
2.f(x+a)=-f(x) T=2a
3.f(x+a)+f(x)=k(k为常数)T=2a
4.f(x+a)=1f(x) T=2a
5.f(x+a).f(x)=k(k为常数) T=2a
?
周期求解常见题
计算周期
2.若f(x)是奇函数,且f(x+1)=-f(x),当x∈(-1,0)时,f(x)=2x+1,求f(92)的值.
?
3.f(x)对任意实数x满足f(x+2)=1????(????), 若f(1)=5, 则f[f(5)]=
?
新课教学
正弦、余弦函数的奇偶性
????
?
?????2
?
?5????2
?
?3????
?
5????2
?
3????
?
问题:你能从它们的图象看出它们有何奇偶性吗?
正弦函数的图象
余弦函数的图象
2????
?
?2????
?
奇偶性
例题讲解
正弦函数奇偶性求值
1.已知f(x)=sin(2x+????),????∈[?????2,????2],且????(?????????6)为偶函数,则????=_____
?
2.已知函数f(x)=-sin(????????+????+????3),(??????
奇偶性
跟踪训练
(2).已知函数f(x)=sin(????+????4+????)是奇函数,则????∈[?????2,????2]时,????的值为____
?
新课教学
正弦函数的对称性
【思考】正弦函数、余弦函数的图象分别关于原点、y轴对称,除此以外它们是否还有其它的对称中心和对称轴呢?
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
新课教学
余弦函数的对称性
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
对称轴:直线x=kπ,k∈Z
对称性
例题讲解
例3???求函数????=cos(2?????????3)的对称轴方程和对称中心坐标.
?
对称性
例题讲解
练习:求下列函数的对称轴、对称中心:
(1)
(2)
对称性
例题讲解
对称性
例题讲解
3.(多选)关于函数f(x)=sin(2x+????3)(x∈R).下列命题正确的是( )
A. y=f(x)可以改写为y=4cos(2x-????6)
B. y=f(x)是以2????为最小正周期为周期函数
C. 函数y=f(x-????6)是奇函数
D. y=f(x+????12)的图像关于y轴对称·
?
对称性
例题讲解
奇偶性周期性的综合运用
奇偶性周期性的综合运用
3.已知函数f(x)是定义在R上的偶函数,且y=f(x)的图像关于直线x=2对称.
(1)证明:f(x)是周期函数
(2)若当x∈[-2,2]时,f(x)=-????2+1,当????∈[?6,?2]时,????(????)的解析式.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
