抽象函数1[上学期]
图片预览





文档简介
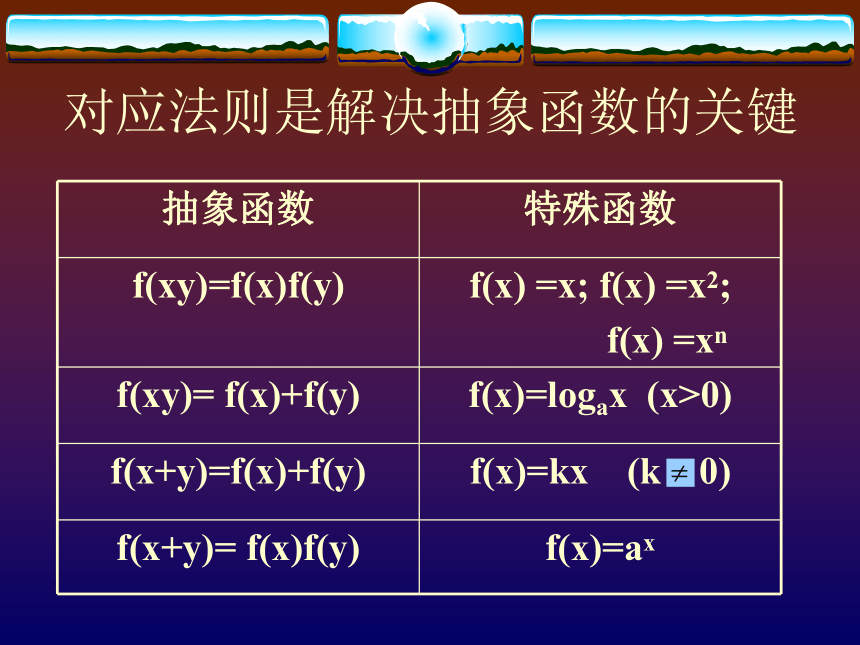
课件15张PPT。抽象函数的常用解法抽象函数:一般是只给出函数符号及条件,或给出函数关系,而没有给出具体解析式和图象的函数。在高考中,常以抽象函数为载体,考查函数的定义域,值域,单调性,奇偶性,周期性及图象问题。2002年,2004年,2005年的高考都出现了这种题型。对应法则是解决抽象函数的关键变式:函数f(x)的定义域为R,对 任意实数x,y都有f(xy)= f(x)+f(y) ,求 f(0) ,f(1)。
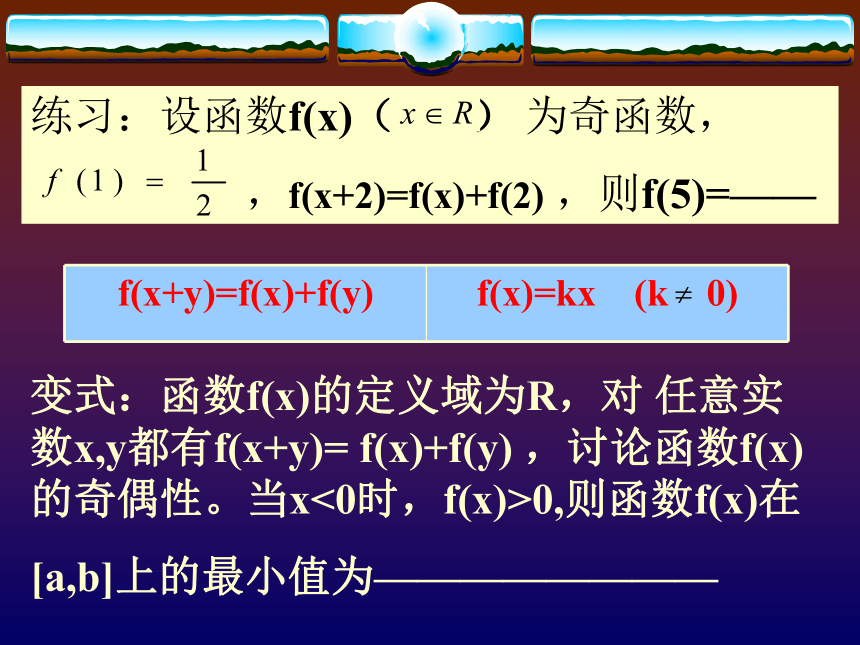
并讨论函数f(x)的奇偶性。变式:函数f(x)的定义域为R,对 任意实数x,y都有f(x+y)= f(x)+f(y) ,讨论函数f(x)的奇偶性。当x<0时,f(x)>0,则函数f(x)在
[a,b]上的最小值为———————— 题后反思
题型:
方法:
填空题,选择题1、特殊法
(化抽象函数为具体函数)3、直接法(按对应法则来处理)2、赋值法练习:函数f(x)是定义在R上的以3为周期的奇函数,且f(2)=0,则方程f(x)=0在区间(0,6)内的解的 个数的最小值为
A 4 B 5 C 6 D 7 题后反思
考查的知识点:
方法:
函数的周期性,
奇偶性,对称性图象法(化无形为有形)例4、 已知f (x)是定义在R上的不恒为零的函数,且对于任意的 ,都 满足f(ab)= af(b)+bf(a)
(1)求f (0), f (1)的值;
(2)判断f (x)的奇偶性,并证明你的结论;
(3)练习:1.定义在R上的函数f(x)满足:f(x+y)=f(x)+f(y)对任意x、y属于R都成立,则f(x)一定是( )
A.偶函数 B.奇函数 C.既奇又偶函数 D.非奇非偶函数2.已知f(x)是定义在R上的不恒为零的函数,且对任意x,y属于R,都满足f(xy)=xf(y)+yf(x). (1)求f(0),f(1); (2)判断f(x)的奇偶性并给出证明.3.定义在R上的函数f(x),对任意x,y属于R,都有f(x-y)+f(x+y)=2f(x)f(y),且f(0)不等于0. (1)求f(0); (2)判断f(x)的奇偶性; (3)若存在非零实数c,使f(c)=0,求证f(x)是周期函数.课堂小结:1、抽象函数问题常涉及函数的单调性、奇偶性、周期性、对称性等函数性质,为此必须熟练掌握上述各性质,方能较好地解决此类问题。2.抽象函数问题的一般解法是:对客观题可采用赋值验证,借助模型函数分析,数形结合和直接推证等方法;而对于主观题,则采用合理赋值与直接推证法,借助于模型函数可以帮助打开解题思路.
并讨论函数f(x)的奇偶性。变式:函数f(x)的定义域为R,对 任意实数x,y都有f(x+y)= f(x)+f(y) ,讨论函数f(x)的奇偶性。当x<0时,f(x)>0,则函数f(x)在
[a,b]上的最小值为———————— 题后反思
题型:
方法:
填空题,选择题1、特殊法
(化抽象函数为具体函数)3、直接法(按对应法则来处理)2、赋值法练习:函数f(x)是定义在R上的以3为周期的奇函数,且f(2)=0,则方程f(x)=0在区间(0,6)内的解的 个数的最小值为
A 4 B 5 C 6 D 7 题后反思
考查的知识点:
方法:
函数的周期性,
奇偶性,对称性图象法(化无形为有形)例4、 已知f (x)是定义在R上的不恒为零的函数,且对于任意的 ,都 满足f(ab)= af(b)+bf(a)
(1)求f (0), f (1)的值;
(2)判断f (x)的奇偶性,并证明你的结论;
(3)练习:1.定义在R上的函数f(x)满足:f(x+y)=f(x)+f(y)对任意x、y属于R都成立,则f(x)一定是( )
A.偶函数 B.奇函数 C.既奇又偶函数 D.非奇非偶函数2.已知f(x)是定义在R上的不恒为零的函数,且对任意x,y属于R,都满足f(xy)=xf(y)+yf(x). (1)求f(0),f(1); (2)判断f(x)的奇偶性并给出证明.3.定义在R上的函数f(x),对任意x,y属于R,都有f(x-y)+f(x+y)=2f(x)f(y),且f(0)不等于0. (1)求f(0); (2)判断f(x)的奇偶性; (3)若存在非零实数c,使f(c)=0,求证f(x)是周期函数.课堂小结:1、抽象函数问题常涉及函数的单调性、奇偶性、周期性、对称性等函数性质,为此必须熟练掌握上述各性质,方能较好地解决此类问题。2.抽象函数问题的一般解法是:对客观题可采用赋值验证,借助模型函数分析,数形结合和直接推证等方法;而对于主观题,则采用合理赋值与直接推证法,借助于模型函数可以帮助打开解题思路.
