2022-2023学年沪科版数学九年级上学期 期末检测题(含答案)
文档属性
| 名称 | 2022-2023学年沪科版数学九年级上学期 期末检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 09:17:35 | ||
图片预览



文档简介
九年级上学期期末检测 数学试卷(沪科版)
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 已知线段a、b、c、d是成比例线段,,,,那么d的值是( )
A. B. 2 C. 3 D. 8
2. 的值等于( )
A. 2 B. 1 C. D.
3. 若函数是二次函数,则( )
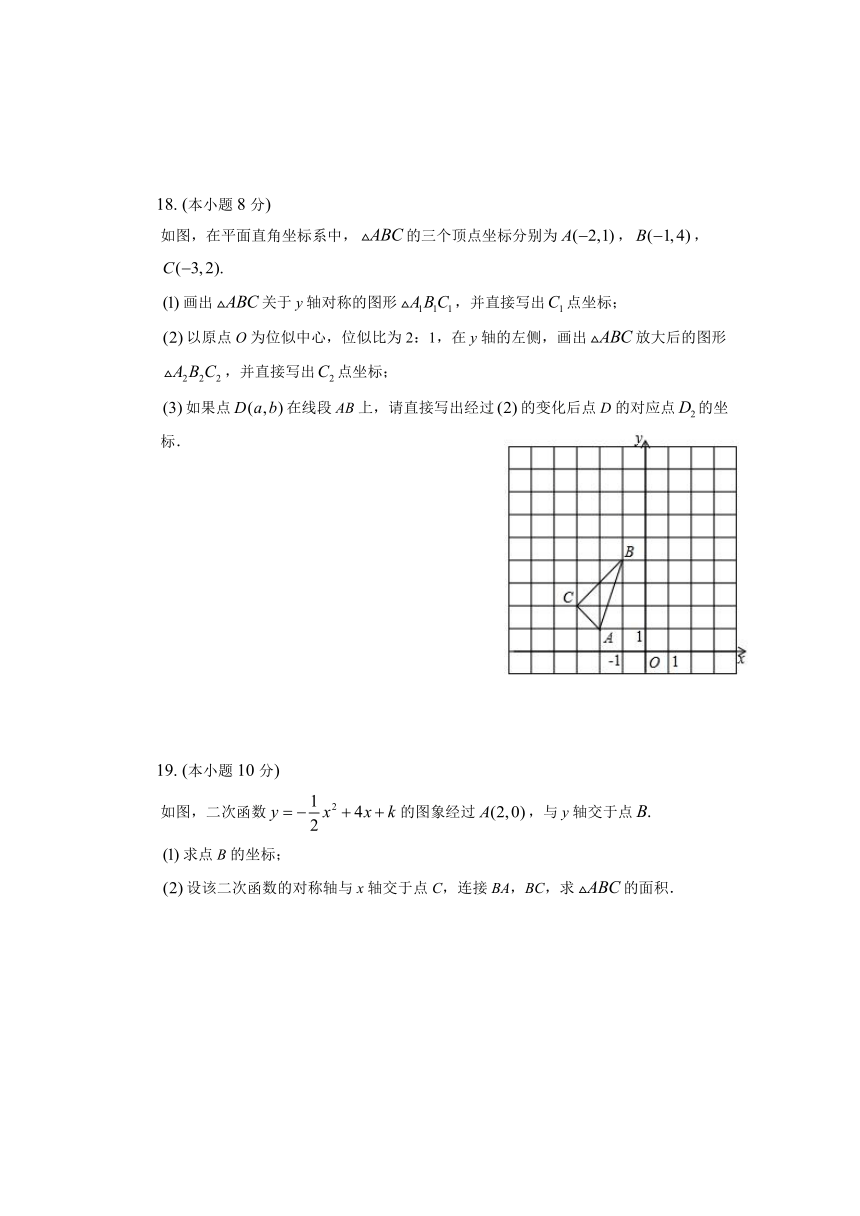
A. B. C. D.
4. 如图所示的是二次函数的部分图象,由图象可知不等式的解集是( )
A. B.
C. 且 D. 或
5. 已知与相似,且相似比为3:2,则与的面积比为( )
A. 1:1 B. 3:2 C. 6:2 D. 9:4
6. 如图,在中,,,则图中相似三角形共有( )
A. 1对 B. 2对
C. 3对 D. 4对
7. 若点,,在反比例函数的图象上,则,,大小关系是( )
A. B. C. D.
8. 某旅行社有100张床位,每床每晚收费100元时,可全部租出,每床每晚收费提高20元,则有10张床位未租出;若每床每晚收费再提高20元,则再减少10张床位未租出;以每次提高20元的这种方法变化下去,为了使收入最大,每床每晚收费应提高( )
A. 40元或60元 B. 40元 C. 60元 D. 80元
9. 如图,在中,,,,于D,设,则的值为( )
A. B.
C. D.
2、 填空题(本大题共4小题,共20分)
11.抛物线是由原抛物线先向左平移3个单位,再向下平移2个单位得到,则原抛物线解析式为__________.
12. 已知,则k的值是_________
13. 如图,平行四边形ABCD的顶点分别在与的图象上,AD边与x轴交于P,若平行四ABCD的面积为12,,则k的值为______.
14. 如图,有一正方形ABCD,边长为,E是边CD上的中点,对角线BD上有一动点F,当与相似时,BF的值为______.
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题8分)
计算:
16. (本小题8分)
若是二次函数,求m的值.
17. (本小题8分)
已知:如图,线段,于点B,且,在DA上截取在AB上截取
求证:点C是线段AB的黄金分割点.
18. (本小题8分)
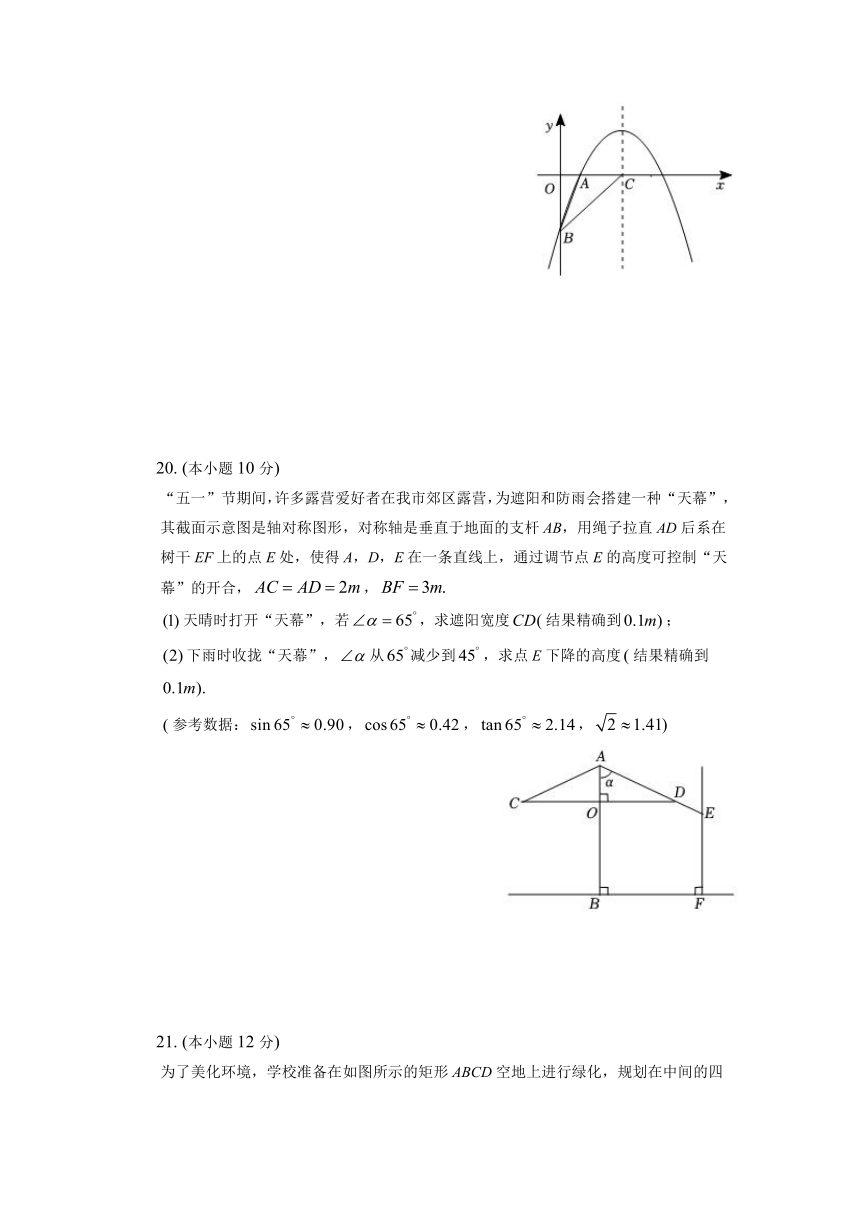
如图,在平面直角坐标系中,的三个顶点坐标分别为,,
画出关于y轴对称的图形,并直接写出点坐标;
以原点O为位似中心,位似比为2:1,在y轴的左侧,画出放大后的图形,并直接写出点坐标;
EMBED Equation.DSMT4 如果点在线段AB上,请直接写出经过的变化后点D的对应点的坐标.
19. (本小题10分)
如图,二次函数的图象经过,与y轴交于点
求点B的坐标;
设该二次函数的对称轴与x轴交于点C,连接BA,BC,求的面积.
20. (本小题10分)
“五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E处,使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,,
天晴时打开“天幕”,若,求遮阳宽度结果精确到;
下雨时收拢“天幕”,从减少到,求点E下降的高度结果精确到
参考数据:,,,
21. (本小题12分)
为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的四边形MNPQ区域里种花,其余的四块三角形上铺设草坪,要求,已知米,米,设米,种花的面积为平方米,草坪面积为平方米.
分别求和与x之间的函数关系式不要求写出自变量的取值范围;
当AN的长为多少米时,种花的面积为640平方米?
22. (本小题12分)
如图,在平面直角坐标系xOy中,抛物线与x轴交于点,,与y轴交于点C,顶点为
求抛物线解析式及点C,点D的坐标:
是抛物线上一动点,且,求直线PB与y轴的交点坐标.
23. (本小题14分)
在中,P是BC边上任意一点,交AC于E,交AB于
求证:;
若,且BC边上的高,设,用含x的式子表示的面积;
问点P在BC上什么位置时,的面积最大?
【答案】
1. D 2. B 3. A 4. A 5. D 6. C 7. D 8. A 9. A 10. D
11. 12. 2或
13. 6 14. 6或8
15. 解:
16. 解:由题意得:,且,
解得:
17. 证明:,,
于点B,
,
,
,
,
点C是线段AB的黄金分割点.
18. 解:如图所示:,即为所求,点坐标为;
如图所示:,即为所求,点坐标为;
点的坐标为
19. 解:把,代入得,
这个二次函数的解析式为,
当时,,
;
,
这个二次函数图象的顶点坐标为,
,
,
的面积
20. 解:由对称知,,,,
在中,,
,
,
,
答:遮阳宽度CD约为米;
如图,
过点E作于H,
,
,,
,
,
,
在中,,
,
当时,,
当时,,
当从减少到时,点E下降的高度约为
21. 解:由题意可得,
米,则米,米,
草坪面积为,
种花的面积为,
由上可得:与x之间的函数关系式是,与x之间的函数关系式是;
令,可得:,
解得,,
即当AN的长为16米或20米时,种花的面积为640平方米.
22. 解:抛物线的表达式为:,
故点,函数的对称轴为:,故点;
由点B、C的坐标知,,
设直线BP交抛物线于点P交y轴于点H,函数对称轴交x轴于点N,
,
设:,则,,
则,解得:
,,
故点,
由点BM的坐标得,直线BM的表达式为:,
故点,
即直线PB与y轴的交点坐标为
23. 证明:,,
四边形AFPE是平行四边形,
解:方法一:如图,
,BC边上的高,
,
,
,
,
,
,
,
同理,得到,相似,
,
,
同理,得到,
,
点E到PE的距离与点F到AE的距离相等,
由知,
,
方法二:如图,
作于G,作于H,
,且BC边上的高,
,
,
,
,
,
,
,
,
同理可求
下同方法一.
解:设,,,
则,
由知,
,
,
同理,得到,
四边形AFPE是平行四边形,
,
,
,
当时,面积有最大值,
当P为BC中点时,的面积最大.
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 已知线段a、b、c、d是成比例线段,,,,那么d的值是( )
A. B. 2 C. 3 D. 8
2. 的值等于( )
A. 2 B. 1 C. D.
3. 若函数是二次函数,则( )
A. B. C. D.
4. 如图所示的是二次函数的部分图象,由图象可知不等式的解集是( )
A. B.
C. 且 D. 或
5. 已知与相似,且相似比为3:2,则与的面积比为( )
A. 1:1 B. 3:2 C. 6:2 D. 9:4
6. 如图,在中,,,则图中相似三角形共有( )
A. 1对 B. 2对
C. 3对 D. 4对
7. 若点,,在反比例函数的图象上,则,,大小关系是( )
A. B. C. D.
8. 某旅行社有100张床位,每床每晚收费100元时,可全部租出,每床每晚收费提高20元,则有10张床位未租出;若每床每晚收费再提高20元,则再减少10张床位未租出;以每次提高20元的这种方法变化下去,为了使收入最大,每床每晚收费应提高( )
A. 40元或60元 B. 40元 C. 60元 D. 80元
9. 如图,在中,,,,于D,设,则的值为( )
A. B.
C. D.
2、 填空题(本大题共4小题,共20分)
11.抛物线是由原抛物线先向左平移3个单位,再向下平移2个单位得到,则原抛物线解析式为__________.
12. 已知,则k的值是_________
13. 如图,平行四边形ABCD的顶点分别在与的图象上,AD边与x轴交于P,若平行四ABCD的面积为12,,则k的值为______.
14. 如图,有一正方形ABCD,边长为,E是边CD上的中点,对角线BD上有一动点F,当与相似时,BF的值为______.
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题8分)
计算:
16. (本小题8分)
若是二次函数,求m的值.
17. (本小题8分)
已知:如图,线段,于点B,且,在DA上截取在AB上截取
求证:点C是线段AB的黄金分割点.
18. (本小题8分)
如图,在平面直角坐标系中,的三个顶点坐标分别为,,
画出关于y轴对称的图形,并直接写出点坐标;
以原点O为位似中心,位似比为2:1,在y轴的左侧,画出放大后的图形,并直接写出点坐标;
EMBED Equation.DSMT4 如果点在线段AB上,请直接写出经过的变化后点D的对应点的坐标.
19. (本小题10分)
如图,二次函数的图象经过,与y轴交于点
求点B的坐标;
设该二次函数的对称轴与x轴交于点C,连接BA,BC,求的面积.
20. (本小题10分)
“五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E处,使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,,
天晴时打开“天幕”,若,求遮阳宽度结果精确到;
下雨时收拢“天幕”,从减少到,求点E下降的高度结果精确到
参考数据:,,,
21. (本小题12分)
为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的四边形MNPQ区域里种花,其余的四块三角形上铺设草坪,要求,已知米,米,设米,种花的面积为平方米,草坪面积为平方米.
分别求和与x之间的函数关系式不要求写出自变量的取值范围;
当AN的长为多少米时,种花的面积为640平方米?
22. (本小题12分)
如图,在平面直角坐标系xOy中,抛物线与x轴交于点,,与y轴交于点C,顶点为
求抛物线解析式及点C,点D的坐标:
是抛物线上一动点,且,求直线PB与y轴的交点坐标.
23. (本小题14分)
在中,P是BC边上任意一点,交AC于E,交AB于
求证:;
若,且BC边上的高,设,用含x的式子表示的面积;
问点P在BC上什么位置时,的面积最大?
【答案】
1. D 2. B 3. A 4. A 5. D 6. C 7. D 8. A 9. A 10. D
11. 12. 2或
13. 6 14. 6或8
15. 解:
16. 解:由题意得:,且,
解得:
17. 证明:,,
于点B,
,
,
,
,
点C是线段AB的黄金分割点.
18. 解:如图所示:,即为所求,点坐标为;
如图所示:,即为所求,点坐标为;
点的坐标为
19. 解:把,代入得,
这个二次函数的解析式为,
当时,,
;
,
这个二次函数图象的顶点坐标为,
,
,
的面积
20. 解:由对称知,,,,
在中,,
,
,
,
答:遮阳宽度CD约为米;
如图,
过点E作于H,
,
,,
,
,
,
在中,,
,
当时,,
当时,,
当从减少到时,点E下降的高度约为
21. 解:由题意可得,
米,则米,米,
草坪面积为,
种花的面积为,
由上可得:与x之间的函数关系式是,与x之间的函数关系式是;
令,可得:,
解得,,
即当AN的长为16米或20米时,种花的面积为640平方米.
22. 解:抛物线的表达式为:,
故点,函数的对称轴为:,故点;
由点B、C的坐标知,,
设直线BP交抛物线于点P交y轴于点H,函数对称轴交x轴于点N,
,
设:,则,,
则,解得:
,,
故点,
由点BM的坐标得,直线BM的表达式为:,
故点,
即直线PB与y轴的交点坐标为
23. 证明:,,
四边形AFPE是平行四边形,
解:方法一:如图,
,BC边上的高,
,
,
,
,
,
,
,
同理,得到,相似,
,
,
同理,得到,
,
点E到PE的距离与点F到AE的距离相等,
由知,
,
方法二:如图,
作于G,作于H,
,且BC边上的高,
,
,
,
,
,
,
,
,
同理可求
下同方法一.
解:设,,,
则,
由知,
,
,
同理,得到,
四边形AFPE是平行四边形,
,
,
,
当时,面积有最大值,
当P为BC中点时,的面积最大.
同课章节目录
