5.2.2 平行线的判定 课件(共29张PPT)
文档属性
| 名称 | 5.2.2 平行线的判定 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 12:39:10 | ||
图片预览







文档简介
(共29张PPT)
第五章 相交线与平行线
5.2 平行线及其判定
5.2.2 平行线的判定
学习目标
1.掌握平行线的三个判定定理.
2.能够灵活运用平行线的三个判定定理进行简单推理与计算.
重点:平行线的三个判定定理的理解与简单运用.
难点:正确使用推理的基本格式.
课前预习
互补
相等
相等
如图,以下说法正确的是( )
A.∠1和∠2是内错角 B.∠2和∠3是同位角
C.∠1和∠3是内错角 D.∠2和∠4是同旁内角
C
旧知回顾
根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否相交来判定是否平行,那么有没有其他判定方法呢?
思考
知识点
平行线的判定方法 1、2、3
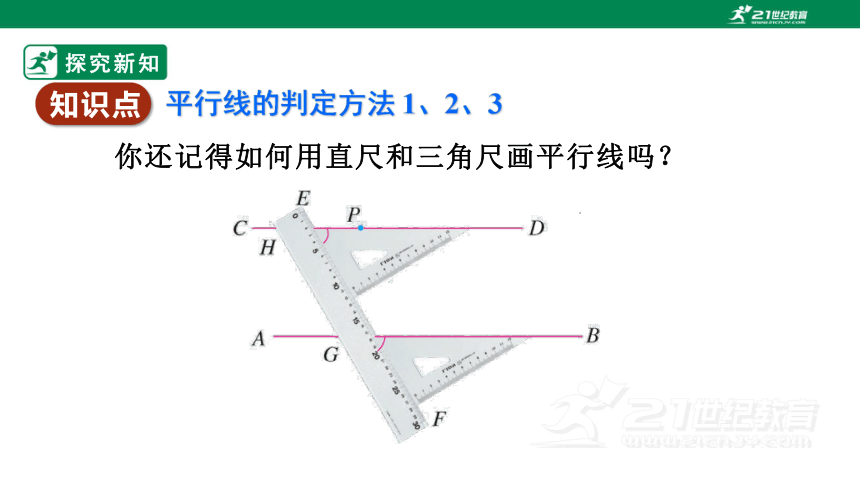
你还记得如何用直尺和三角尺画平行线吗?
探究新知
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
∠1 =∠2
简化
同位角相等,两直线平行.
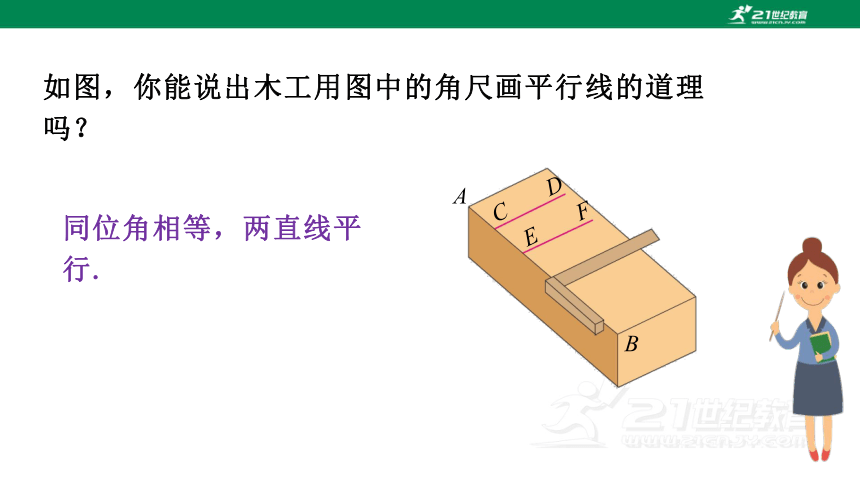
如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
如图,如果∠2 =∠3,那么 a 与 b 平行吗?
因为∠2 =∠3,∠3 =∠1,
所以∠1 =∠2,
所以 a∥b .
思考
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
如图,如果∠2 +∠4 = 180°,那么 a 与 b 平行吗?
因为∠2 +∠4 = 180°,
∠1 +∠4 = 180°,
所以∠1 = ∠2,
所以 a∥b .
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
判定方法 1 同位角相等,两直线平行.
判定方法 2 内错角相等,两直线平行.
判定方法 3 同旁内角互补,两直线平行.
平行线的判定
归纳
同一平面内,同垂直于第三条直线的两直线平行
思考
例 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
已知条件:直线 b 与直线 c 都垂直于直线 a .
要说明的结论:直线 b 与直线 c 平行吗?
知识点
1. 如图, BE 是 AB 的延长线.
(1)由∠CBE =∠A 可以判定哪两条直线平行?根据是什么?
答: AD∥BC . 根据同位角相等,两直线平行.
课堂练习
(2)由∠CBE =∠C 可以判定哪两条直线平行?根据是什么?
答: AE∥CD . 根据内错角相等,两直线平行.
答: AE∥CD . 根据同旁内角互补,两直线平行.
(3)由∠D +∠A = 180°可以判定哪两条直线平行?根据是什么?
2. 在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2 是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么?
解:①可度量∠3 的度数,因为∠3 与∠2是同旁内角,若∠3=90°,则∠3+∠2=180°.根据“同旁内角互补,两直线平行”可得两条直轨平行.
②也可度量∠4 的度数,因为∠4 与∠2 是同位角,若∠4=90°,则∠4=∠2. 根据“同位角相等,两直线平行”可得两条直轨平行.
③还可度量∠5 的度数,因为∠5 与∠2 是内错角,若∠5=90°,则∠5=∠2. 根据“内错角相等,两直线平行”可得两条直轨平行.
3.如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横线互相平行吗?你有多少种判别方法?
答:平行 . 理由不唯一.
平行线的判定:
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单地说,就是同位角相等,两直线平行
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单地说,就是内错角相等,两直线平行
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,就是同旁内角互补,两直线平行
知识归纳
例1 如图,若∠1=∠4,∠1+∠2=180°,
则AB,CD,EF的位置关系如何?
解:∵∠1+∠2=180°,∠2+∠3=180°,
∴∠1=∠3,∴AB∥CD.
又∵∠1=∠4,
∴AB∥EF,∴AB∥CD∥EF.
例题分析
例2 如图,已知CB平分∠ACD,且∠1=∠2,AB与CD平行吗?为什么?
解:AB∥CD.
理由如下:∵CB平分∠ACD,
∴∠1=∠BCD.
∵∠1=∠2,
∴∠2=∠BCD,∴AB∥CD.
例题分析
1.如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
2.如图,若∠1=∠2,则DE∥AB;若∠2=∠3,则BC∥_____.
C
EF
课堂练习
3.如图,已知AB⊥AD,CD⊥AD,∠1=∠2,那么直线AE,DF平行吗?为什么?
解:AE与DF平行.
理由如下:∵AB⊥AD,CD⊥AD,
∴∠BAD=∠ADC=90°.
又∵∠1=∠2,
∴∠BAD-∠1=∠ADC-∠2,
即∠DAE=∠ADF,
∴AE∥DF.
课堂练行线的判定
①平行公理的推论:如果两条直线都与第三条直线平行,这两条直线也互相平行.
②判定方法 1:同位角相等,两直线平行.
③判定方法 2:内错角相等,两直线平行.
④判定方法 3:同旁内角互补,两直线平行.
⑤同一平面内,垂直于同一直线的两条直线平行.
应用:判定生活中的平行线
课堂小结
1.教材P15~16习题5.2第1,2,4 ,7题;
2.完成对应课时练习.
布置作业
第五章 相交线与平行线
5.2 平行线及其判定
5.2.2 平行线的判定
学习目标
1.掌握平行线的三个判定定理.
2.能够灵活运用平行线的三个判定定理进行简单推理与计算.
重点:平行线的三个判定定理的理解与简单运用.
难点:正确使用推理的基本格式.
课前预习
互补
相等
相等
如图,以下说法正确的是( )
A.∠1和∠2是内错角 B.∠2和∠3是同位角
C.∠1和∠3是内错角 D.∠2和∠4是同旁内角
C
旧知回顾
根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否相交来判定是否平行,那么有没有其他判定方法呢?
思考
知识点
平行线的判定方法 1、2、3
你还记得如何用直尺和三角尺画平行线吗?
探究新知
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
∠1 =∠2
简化
同位角相等,两直线平行.
如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
如图,如果∠2 =∠3,那么 a 与 b 平行吗?
因为∠2 =∠3,∠3 =∠1,
所以∠1 =∠2,
所以 a∥b .
思考
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
如图,如果∠2 +∠4 = 180°,那么 a 与 b 平行吗?
因为∠2 +∠4 = 180°,
∠1 +∠4 = 180°,
所以∠1 = ∠2,
所以 a∥b .
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
判定方法 1 同位角相等,两直线平行.
判定方法 2 内错角相等,两直线平行.
判定方法 3 同旁内角互补,两直线平行.
平行线的判定
归纳
同一平面内,同垂直于第三条直线的两直线平行
思考
例 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
已知条件:直线 b 与直线 c 都垂直于直线 a .
要说明的结论:直线 b 与直线 c 平行吗?
知识点
1. 如图, BE 是 AB 的延长线.
(1)由∠CBE =∠A 可以判定哪两条直线平行?根据是什么?
答: AD∥BC . 根据同位角相等,两直线平行.
课堂练习
(2)由∠CBE =∠C 可以判定哪两条直线平行?根据是什么?
答: AE∥CD . 根据内错角相等,两直线平行.
答: AE∥CD . 根据同旁内角互补,两直线平行.
(3)由∠D +∠A = 180°可以判定哪两条直线平行?根据是什么?
2. 在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2 是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么?
解:①可度量∠3 的度数,因为∠3 与∠2是同旁内角,若∠3=90°,则∠3+∠2=180°.根据“同旁内角互补,两直线平行”可得两条直轨平行.
②也可度量∠4 的度数,因为∠4 与∠2 是同位角,若∠4=90°,则∠4=∠2. 根据“同位角相等,两直线平行”可得两条直轨平行.
③还可度量∠5 的度数,因为∠5 与∠2 是内错角,若∠5=90°,则∠5=∠2. 根据“内错角相等,两直线平行”可得两条直轨平行.
3.如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横线互相平行吗?你有多少种判别方法?
答:平行 . 理由不唯一.
平行线的判定:
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单地说,就是同位角相等,两直线平行
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单地说,就是内错角相等,两直线平行
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,就是同旁内角互补,两直线平行
知识归纳
例1 如图,若∠1=∠4,∠1+∠2=180°,
则AB,CD,EF的位置关系如何?
解:∵∠1+∠2=180°,∠2+∠3=180°,
∴∠1=∠3,∴AB∥CD.
又∵∠1=∠4,
∴AB∥EF,∴AB∥CD∥EF.
例题分析
例2 如图,已知CB平分∠ACD,且∠1=∠2,AB与CD平行吗?为什么?
解:AB∥CD.
理由如下:∵CB平分∠ACD,
∴∠1=∠BCD.
∵∠1=∠2,
∴∠2=∠BCD,∴AB∥CD.
例题分析
1.如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
2.如图,若∠1=∠2,则DE∥AB;若∠2=∠3,则BC∥_____.
C
EF
课堂练习
3.如图,已知AB⊥AD,CD⊥AD,∠1=∠2,那么直线AE,DF平行吗?为什么?
解:AE与DF平行.
理由如下:∵AB⊥AD,CD⊥AD,
∴∠BAD=∠ADC=90°.
又∵∠1=∠2,
∴∠BAD-∠1=∠ADC-∠2,
即∠DAE=∠ADF,
∴AE∥DF.
课堂练行线的判定
①平行公理的推论:如果两条直线都与第三条直线平行,这两条直线也互相平行.
②判定方法 1:同位角相等,两直线平行.
③判定方法 2:内错角相等,两直线平行.
④判定方法 3:同旁内角互补,两直线平行.
⑤同一平面内,垂直于同一直线的两条直线平行.
应用:判定生活中的平行线
课堂小结
1.教材P15~16习题5.2第1,2,4 ,7题;
2.完成对应课时练习.
布置作业
