正弦定理余弦定理[下学期]
图片预览



文档简介
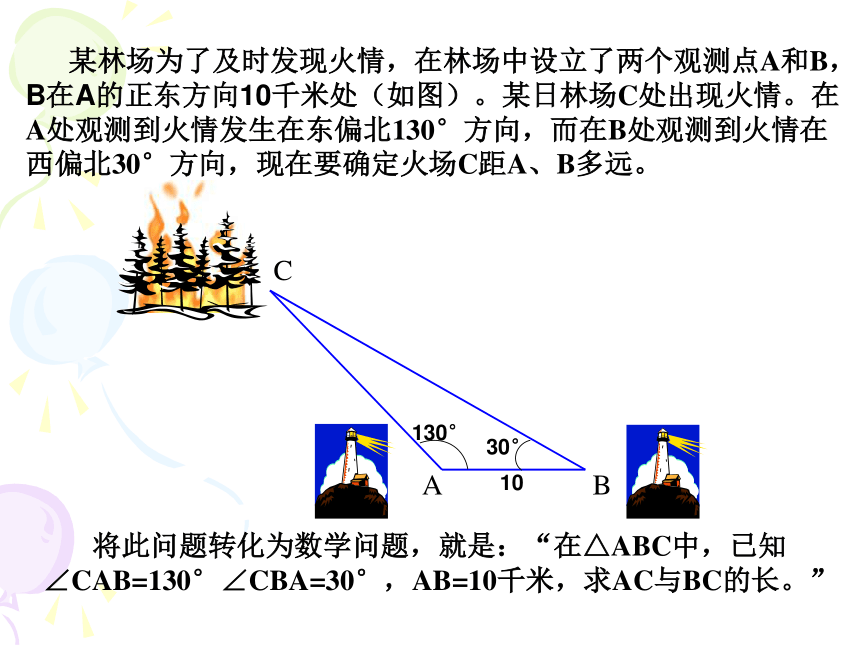
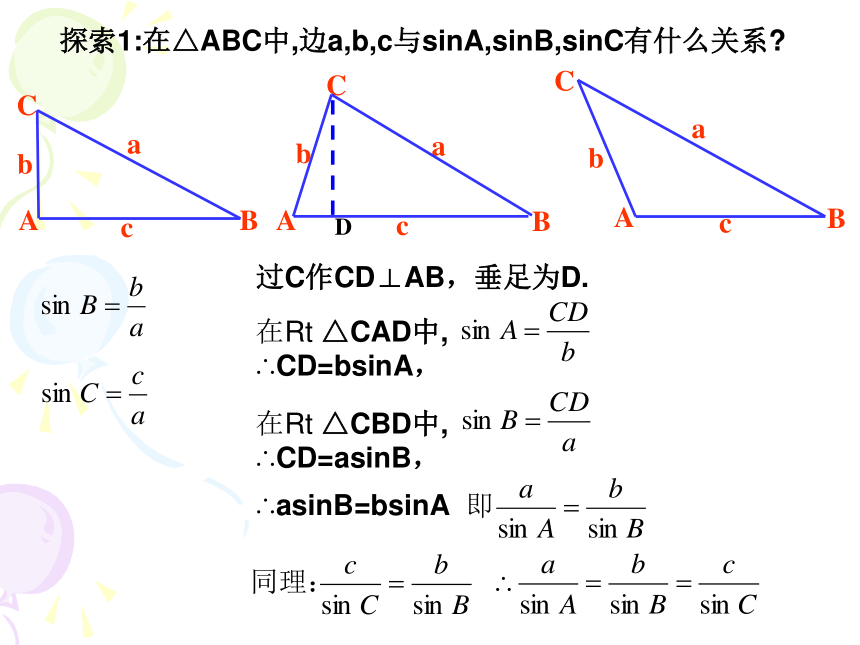
课件13张PPT。30° 某林场为了及时发现火情,在林场中设立了两个观测点A和B, B在A的正东方向10千米处(如图)。某日林场C处出现火情。在A处观测到火情发生在东偏北130°方向,而在B处观测到火情在西偏北30°方向,现在要确定火场C距A、B多远。 将此问题转化为数学问题,就是:“在△ABC中,已知∠CAB=130°∠CBA=30°,AB=10千米,求AC与BC的长。”CAB130°10正弦定理、余弦定理探索1:在△ABC中,边a,b,c与sinA,sinB,sinC有什么关系?D过C作CD⊥AB,垂足为D.在Rt △CAD中,
∴CD=bsinA,在Rt △CBD中,
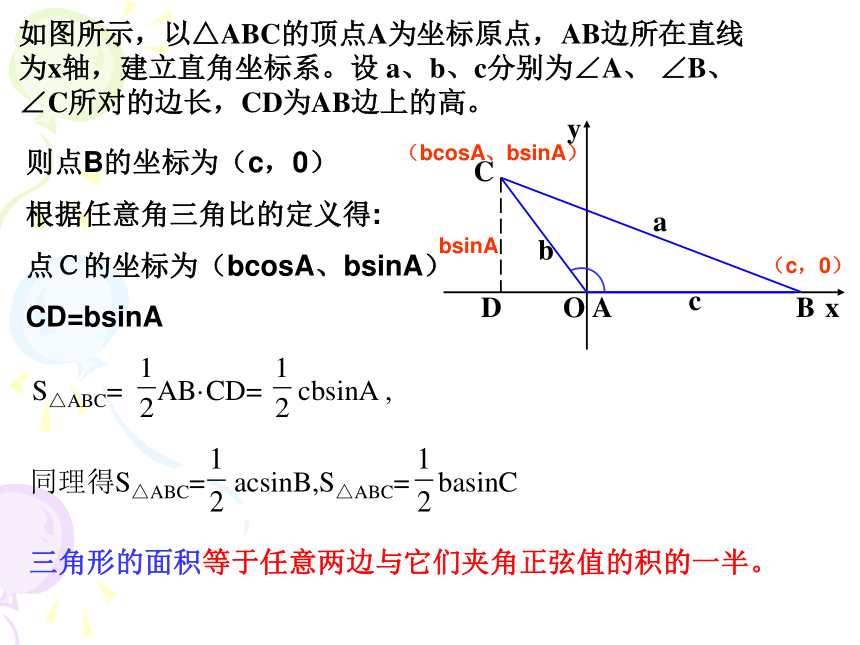
∴CD=asinB,∴asinB=bsinA如图所示,以△ABC的顶点A为坐标原点,AB边所在直线为x轴,建立直角坐标系。设 a、b、c分别为∠A、 ∠B、 ∠C所对的边长,CD为AB边上的高。AyxCDOBabcS△ABC= AB·CD= cbsinA , 同理得S△ABC= acsinB,S△ABC= basinC则点B的坐标为(c,0)
根据任意角三角比的定义得:
点C的坐标为(bcosA、bsinA)
CD=bsinA(c,0)(bcosA、bsinA)bsinA三角形的面积等于任意两边与它们夹角正弦值的积的一半。将上述等式同时除以 abc,得正弦定理:
在三角形中,各边与它所对角的正弦的比相等。解:解:∴∠A=45°或135°让我们回到本节开头所提出的问题:解:由三角形内角和为180°,可知
C=180°-130°-30°=20°由正弦定理因此,火场C在距离观测点A东偏北130°方向的约15千米处,在距离观测点B西偏北30°方向的约22千米处。在△ABC中,已知∠CAB=130°∠CBA=30°,AB=10千米,求AC与BC的长。(精确到千米)即 a2=b2+c2-2bccosA(c,0)即 a2=b2+c2-2bccosA探索2:如图,在△ABC中,已知AB=c,AC=b, ∠A, 能否利用正弦定理求得第三边? AACBbcyxOa(bcosA、bsinA)a2=(bcosA-c)2+b2sin2A=b2cos2A-2bccosA+c2+b2sin2A=b2-2bccosA+c2由两点间的距离公式得:aA同理可得 b2=a2+c2-2accosB
c2=a2+b2-2abcosCbbcc即 a2=b2+c2-2bccosA a2=b2+c2-2bccosAb2=a2+c2-2accosB
c2=a2+b2-2abcosC余弦定理:三角形的一边的平方等于其它两边的平方和减去这两边与它们夹角的余弦值乘积的两倍。余弦定理也可以写成下面的形式:ACDB小结:
1、利用三角形面积公式推导了正弦定理
2、利用两点间距离公式推导了余弦定理
3、初步知道利用定理解三角形的问题谢谢光临指导
∴CD=bsinA,在Rt △CBD中,
∴CD=asinB,∴asinB=bsinA如图所示,以△ABC的顶点A为坐标原点,AB边所在直线为x轴,建立直角坐标系。设 a、b、c分别为∠A、 ∠B、 ∠C所对的边长,CD为AB边上的高。AyxCDOBabcS△ABC= AB·CD= cbsinA , 同理得S△ABC= acsinB,S△ABC= basinC则点B的坐标为(c,0)
根据任意角三角比的定义得:
点C的坐标为(bcosA、bsinA)
CD=bsinA(c,0)(bcosA、bsinA)bsinA三角形的面积等于任意两边与它们夹角正弦值的积的一半。将上述等式同时除以 abc,得正弦定理:
在三角形中,各边与它所对角的正弦的比相等。解:解:∴∠A=45°或135°让我们回到本节开头所提出的问题:解:由三角形内角和为180°,可知
C=180°-130°-30°=20°由正弦定理因此,火场C在距离观测点A东偏北130°方向的约15千米处,在距离观测点B西偏北30°方向的约22千米处。在△ABC中,已知∠CAB=130°∠CBA=30°,AB=10千米,求AC与BC的长。(精确到千米)即 a2=b2+c2-2bccosA(c,0)即 a2=b2+c2-2bccosA探索2:如图,在△ABC中,已知AB=c,AC=b, ∠A, 能否利用正弦定理求得第三边? AACBbcyxOa(bcosA、bsinA)a2=(bcosA-c)2+b2sin2A=b2cos2A-2bccosA+c2+b2sin2A=b2-2bccosA+c2由两点间的距离公式得:aA同理可得 b2=a2+c2-2accosB
c2=a2+b2-2abcosCbbcc即 a2=b2+c2-2bccosA a2=b2+c2-2bccosAb2=a2+c2-2accosB
c2=a2+b2-2abcosC余弦定理:三角形的一边的平方等于其它两边的平方和减去这两边与它们夹角的余弦值乘积的两倍。余弦定理也可以写成下面的形式:ACDB小结:
1、利用三角形面积公式推导了正弦定理
2、利用两点间距离公式推导了余弦定理
3、初步知道利用定理解三角形的问题谢谢光临指导
