直线与圆的位置关系[上学期]
图片预览







文档简介
课件26张PPT。直线与圆的位置关系湛江一中高中数学组知识梳理判定直线 与圆的位置关系的方法有两种:(1)代数法:由直线 与圆的公共点的个数 来判断。(2)几何法:由圆心到直线的距离d与半径r的关系来判断。在实际应用中,常采用第二种方法判定。直线方程:
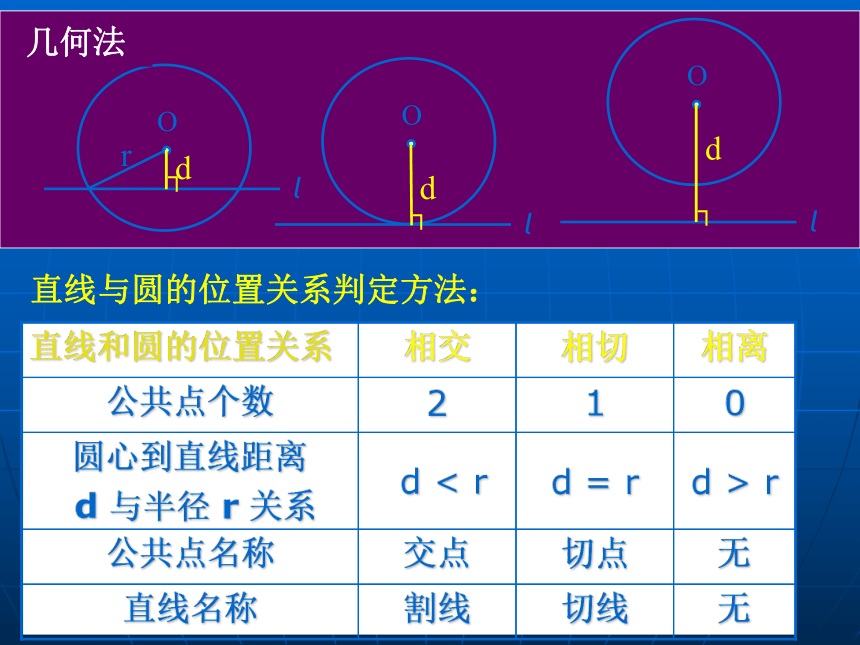
圆方程:联立方程组得一元二次方程判别式代数法直线与圆的位置关系判定方法:直线名称公共点名称圆心到直线距离
d 与半径 r 关系公共点个数相离相切相交直线和圆的位置关系几何法点击双基1、圆x2+y2-4x+4y+6=0截直线x-y-5=0所
得的弦长等于
B. C.1 D.5
2、圆x2+y2-4x=0在点P(1, )处的切线方程为
A.x+ y-2=0 B.x+ y-4=0
C.x- y+4=0 D.x- y+2=0
3、设m>0,则直线 (x+y)+1+m=0与圆
x2+y2=m的位置关系为
A.相切 B.相交
C.相切或相离 D.相交或相切点击双基1、圆x2+y2-4x+4y+6=0截直线x-y-5=0所
得的弦长等于
B. C.1 D.5
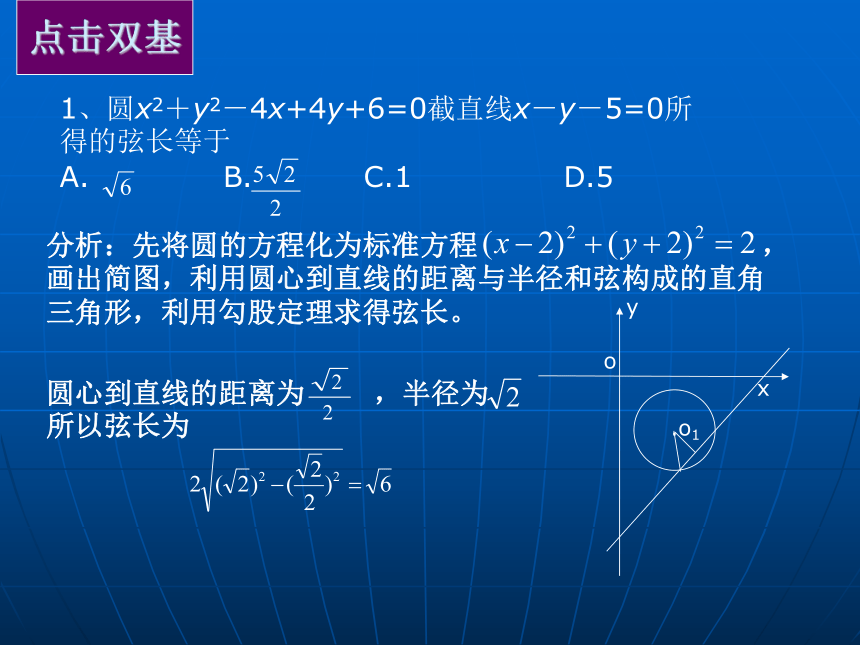
分析:先将圆的方程化为标准方程 ,
画出简图,利用圆心到直线的距离与半径和弦构成的直角
三角形,利用勾股定理求得弦长。圆心到直线的距离为 ,半径为
所以弦长为
点击双基
2、圆x2+y2-4x=0在点P(1, )处的切线方程为
A.x+ y-2=0 B.x+ y-4=0
C.x- y+4=0 D.x- y+2=0
(方法一)解:斜率不存在时,直线为x=1,显然不满足。
设直线斜率为 ,联立直线与圆的方程(方法二) 提示:直接利用过P点的半径与切线垂直,求得斜率
(方法三) 公式法点击双基3、设m>0,则直线 (x+y)+1+m=0与圆
x2+y2=m的位置关系为
A.相切 B.相交
C.相切或相离 D.相交或相切所以直线与圆的位置关系是相切或相离。典例剖析例1、已知 和圆外一点 ,
求过 点的圆的切线方程。(《心之喜》例1 )P .o .Qxy 分析:求直线方程要注意直线的斜率是否存在典例剖析例2、已知圆 与直线
相交于 两点, 为坐标原点,
若 ⊥ ,求 的值。(《心之喜》例2 )分析:本题用几何法较难操作,选用代数法解决。例3、已知圆 ,
直线
(1)证明:不论 取什么实数,直线与圆恒交于两点。
(2)求直线 被圆 截得的弦长最小时的方程。典例剖析分析:直线过定点,而该点在圆内,此题便可证。习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )2、已知 是圆 内异于圆心的一点,
则直线 与此圆有何种位置关系?练习反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1由数形结合可得:习题反馈2、已知 是圆 内异于圆心的一点,
则直线 与此圆有何种位置关系?分析:比较圆心到直线的距离与半径的大小。习题反馈变式1:已知 是圆 上的一点,
则直线 与此圆有何种位置关系?分析:比较圆心到直线的距离与半径的大小。习题反馈变式2:已知 是圆 外的一点,
则直线 与此圆有何种位置关系?分析:比较圆心到直线的距离与半径的大小。课后拓展变式3:如图,已知 是圆 外的一点,
MP、MQ是圆的两条切线,P、Q分别为切点,求切点弦PQ的所在
的直线方程。谢谢各位的光临指导
祝同学们学习进步!
圆方程:联立方程组得一元二次方程判别式代数法直线与圆的位置关系判定方法:直线名称公共点名称圆心到直线距离
d 与半径 r 关系公共点个数相离相切相交直线和圆的位置关系几何法点击双基1、圆x2+y2-4x+4y+6=0截直线x-y-5=0所
得的弦长等于
B. C.1 D.5
2、圆x2+y2-4x=0在点P(1, )处的切线方程为
A.x+ y-2=0 B.x+ y-4=0
C.x- y+4=0 D.x- y+2=0
3、设m>0,则直线 (x+y)+1+m=0与圆
x2+y2=m的位置关系为
A.相切 B.相交
C.相切或相离 D.相交或相切点击双基1、圆x2+y2-4x+4y+6=0截直线x-y-5=0所
得的弦长等于
B. C.1 D.5
分析:先将圆的方程化为标准方程 ,
画出简图,利用圆心到直线的距离与半径和弦构成的直角
三角形,利用勾股定理求得弦长。圆心到直线的距离为 ,半径为
所以弦长为
点击双基
2、圆x2+y2-4x=0在点P(1, )处的切线方程为
A.x+ y-2=0 B.x+ y-4=0
C.x- y+4=0 D.x- y+2=0
(方法一)解:斜率不存在时,直线为x=1,显然不满足。
设直线斜率为 ,联立直线与圆的方程(方法二) 提示:直接利用过P点的半径与切线垂直,求得斜率
(方法三) 公式法点击双基3、设m>0,则直线 (x+y)+1+m=0与圆
x2+y2=m的位置关系为
A.相切 B.相交
C.相切或相离 D.相交或相切所以直线与圆的位置关系是相切或相离。典例剖析例1、已知 和圆外一点 ,
求过 点的圆的切线方程。(《心之喜》例1 )P .o .Qxy 分析:求直线方程要注意直线的斜率是否存在典例剖析例2、已知圆 与直线
相交于 两点, 为坐标原点,
若 ⊥ ,求 的值。(《心之喜》例2 )分析:本题用几何法较难操作,选用代数法解决。例3、已知圆 ,
直线
(1)证明:不论 取什么实数,直线与圆恒交于两点。
(2)求直线 被圆 截得的弦长最小时的方程。典例剖析分析:直线过定点,而该点在圆内,此题便可证。习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )2、已知 是圆 内异于圆心的一点,
则直线 与此圆有何种位置关系?练习反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1习题反馈1、若圆 上有且只有两个点到
直线 的距离等于1,则半径的范围是( )yx. o1由数形结合可得:习题反馈2、已知 是圆 内异于圆心的一点,
则直线 与此圆有何种位置关系?分析:比较圆心到直线的距离与半径的大小。习题反馈变式1:已知 是圆 上的一点,
则直线 与此圆有何种位置关系?分析:比较圆心到直线的距离与半径的大小。习题反馈变式2:已知 是圆 外的一点,
则直线 与此圆有何种位置关系?分析:比较圆心到直线的距离与半径的大小。课后拓展变式3:如图,已知 是圆 外的一点,
MP、MQ是圆的两条切线,P、Q分别为切点,求切点弦PQ的所在
的直线方程。谢谢各位的光临指导
祝同学们学习进步!
