直线和圆 [上下学期通用]
图片预览











文档简介
课件72张PPT。 解析几何重在研究方法,它用代数方法研究几何问题,又把代数问题转化为几何问题解决.即
几何→代数→几何
或 代数→几何→代数 解析几何研究的主要问题是:
(1)依据题设条件,求出表示平面曲线的方程;
(2)通过方程,研究平面曲线的性质.
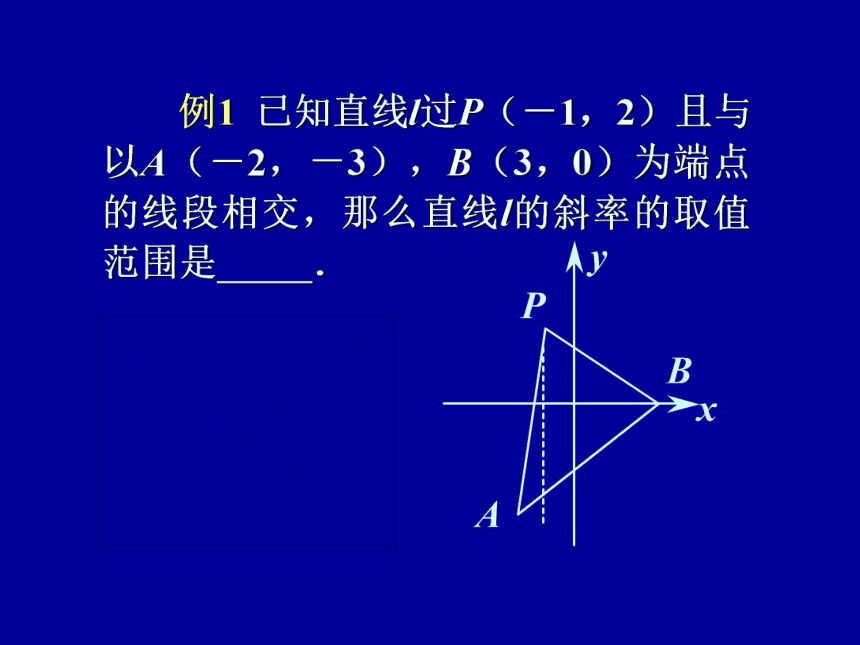
直线和圆是最基本的图形,是高考必涉及的考查内容,研究直线和圆的思想与方法,是研究解析几何的基本思想与方法,也是掌握解析几何的基础. 例1 已知直线l过P(-1,2)且与以A(-2,-3),B(3,0)为端点的线段相交,那么直线l的斜率的取值范围是 . 思路1 观察直线 l 在PA、PB 之间变动时,斜率k 的变化范围.得则直线 l 斜率的取值范围是, 思路2 寻求 l 与AB交点Q分AB成比值λ与l 的斜率k 的关系,利用λ>0 得k 的取值范围.
设直线l的方程为y-2=k(x+1)与AB交于Q(x,y).
若Q不与B重合, Q分 比为λ≥0,则,又当Q、B 重合,l 过点B(3,0),这时∵ Q 在 l 上,∴,得,或 k≥5∴ l 的斜率取值范围是..例3 交于同一点的三条直线是 ( )
A.x+y-2=0,2x+2y+3=0, x-y=1
B.x+y=0,x-y=0, 9x+25y-225=0
C.2x-y+5=0,x+2y+6=0, x+2y-5=0
D.y-3=5(x-2), y-3=-18(x-2),x-y+1=0 思路 先从方程提供的信息分析各直线的位置
易知A、C分别有两直线平行,不可能相交,可排除;
而B中直线x+y=0与x-y=0过原点,第三条直线不过原点,也排除;
D中前两直线过(2,3)点,而此点恰在第三条直线上.
答案选D. 例4 已 知 圆
C :x2+y2-4 x-6y+12=0,求
(Ⅰ)过A(3,5)点的圆C的切线方程;
(Ⅱ)在两坐标轴上截距相等的切线方程.C. D.3 例5 如果直线沿x轴负方向平移3个单位,再沿y轴正方向平移1个单位后,又回到原来的位置,那么直线l的斜率是 ( ) A. B.-3 小结
①通过“点”认识“线”是解析几何常用的方法;
②在平移变换下,点的坐标的变化与方程中变元x,y的变化形式是不同的,二者不可混淆. 小结
①引进参数时,要注意参数的取值范围;
②在把求∠ACB的最值问题转化为求tan∠ACB的最值时,要注意转化的等价性。 思路2 思路1知直线l过A(1,2),
直线 l 不过第四象限 ? l 的倾角不大于OA的倾角,
而kOA=2
故l 的斜率满足0≤k≤2 . 思路3 代值进行判断
当l 的斜率k=2时,直线l方程为 y-2=2(x-1)
即 y=2x 符合条件,由此排除B、C、D项,
得A项.
小结 本题不同的解法反映对基础知识掌握的熟练程度与思维的灵活性层次不 同。选择题要多角度考虑,寻求最优解法。 例9 设圆满足:①截y轴得弦长为2;②被x轴分成两段圆弧,其弧长比 为3︰1;在满足①、②的所有圆中,求圆心到直线l :x+2y=0距离最小的圆的方程.
思路1 由于(a,b)使d取最小值,因此有 |a-2b|=1,舍去a=-1,b=1与a=1, b=-1的情况,只取a=b=1或a=b=-1,故所求圆的方程为
(x-1)2+(y-1)2=2 或
(x+1)2+(y+1)2=2
思路2 用待定系数法确定a,b,r 三个量,需建立三个方程,条件①,②是等量关系,最后的条件用距离的最小值给出,需要将条件转化,找出等量关系. 小结
①几何条件代数化;
②由距离最小值获得第三个等量关系的方法。 圆(x-a)2+(y-b)2=r2 ?
三个参数a,b,r .
圆x2+y2+Dx+Ey+F=0 ?三个参数D,E,F.
(D2+E2-4F>0) 分析 (Ⅰ) 的几何意义是圆上的点与已知点(1,2)连线的斜率,当直线与圆相切时, 取最值;
(Ⅱ)设x-2y=m,m表示一族平行直线在x轴上的截距,当直线x-2y=m与圆相切时,m 取最值. 例11 矩形ABCD的顶点A、B在直线y=2x+m上,C、D在抛物线y2=4x上,该矩形的外接圆方程为 x2+y2-x-4y-t=0 .
(Ⅰ)求矩形ABCD对角线交点M的坐标;
(Ⅱ)求此矩形边长,并确定m,t的值. 已知点A ( a,0 ) (a>0,a ≠1 ) 和 直 线 l :x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程的曲线类型与a 值的关系 .动点C到角两边距离相等动点C在AB上两个方程组成的参数方程引入参数b
几何→代数→几何
或 代数→几何→代数 解析几何研究的主要问题是:
(1)依据题设条件,求出表示平面曲线的方程;
(2)通过方程,研究平面曲线的性质.
直线和圆是最基本的图形,是高考必涉及的考查内容,研究直线和圆的思想与方法,是研究解析几何的基本思想与方法,也是掌握解析几何的基础. 例1 已知直线l过P(-1,2)且与以A(-2,-3),B(3,0)为端点的线段相交,那么直线l的斜率的取值范围是 . 思路1 观察直线 l 在PA、PB 之间变动时,斜率k 的变化范围.得则直线 l 斜率的取值范围是, 思路2 寻求 l 与AB交点Q分AB成比值λ与l 的斜率k 的关系,利用λ>0 得k 的取值范围.
设直线l的方程为y-2=k(x+1)与AB交于Q(x,y).
若Q不与B重合, Q分 比为λ≥0,则,又当Q、B 重合,l 过点B(3,0),这时∵ Q 在 l 上,∴,得,或 k≥5∴ l 的斜率取值范围是..例3 交于同一点的三条直线是 ( )
A.x+y-2=0,2x+2y+3=0, x-y=1
B.x+y=0,x-y=0, 9x+25y-225=0
C.2x-y+5=0,x+2y+6=0, x+2y-5=0
D.y-3=5(x-2), y-3=-18(x-2),x-y+1=0 思路 先从方程提供的信息分析各直线的位置
易知A、C分别有两直线平行,不可能相交,可排除;
而B中直线x+y=0与x-y=0过原点,第三条直线不过原点,也排除;
D中前两直线过(2,3)点,而此点恰在第三条直线上.
答案选D. 例4 已 知 圆
C :x2+y2-4 x-6y+12=0,求
(Ⅰ)过A(3,5)点的圆C的切线方程;
(Ⅱ)在两坐标轴上截距相等的切线方程.C. D.3 例5 如果直线沿x轴负方向平移3个单位,再沿y轴正方向平移1个单位后,又回到原来的位置,那么直线l的斜率是 ( ) A. B.-3 小结
①通过“点”认识“线”是解析几何常用的方法;
②在平移变换下,点的坐标的变化与方程中变元x,y的变化形式是不同的,二者不可混淆. 小结
①引进参数时,要注意参数的取值范围;
②在把求∠ACB的最值问题转化为求tan∠ACB的最值时,要注意转化的等价性。 思路2 思路1知直线l过A(1,2),
直线 l 不过第四象限 ? l 的倾角不大于OA的倾角,
而kOA=2
故l 的斜率满足0≤k≤2 . 思路3 代值进行判断
当l 的斜率k=2时,直线l方程为 y-2=2(x-1)
即 y=2x 符合条件,由此排除B、C、D项,
得A项.
小结 本题不同的解法反映对基础知识掌握的熟练程度与思维的灵活性层次不 同。选择题要多角度考虑,寻求最优解法。 例9 设圆满足:①截y轴得弦长为2;②被x轴分成两段圆弧,其弧长比 为3︰1;在满足①、②的所有圆中,求圆心到直线l :x+2y=0距离最小的圆的方程.
思路1 由于(a,b)使d取最小值,因此有 |a-2b|=1,舍去a=-1,b=1与a=1, b=-1的情况,只取a=b=1或a=b=-1,故所求圆的方程为
(x-1)2+(y-1)2=2 或
(x+1)2+(y+1)2=2
思路2 用待定系数法确定a,b,r 三个量,需建立三个方程,条件①,②是等量关系,最后的条件用距离的最小值给出,需要将条件转化,找出等量关系. 小结
①几何条件代数化;
②由距离最小值获得第三个等量关系的方法。 圆(x-a)2+(y-b)2=r2 ?
三个参数a,b,r .
圆x2+y2+Dx+Ey+F=0 ?三个参数D,E,F.
(D2+E2-4F>0) 分析 (Ⅰ) 的几何意义是圆上的点与已知点(1,2)连线的斜率,当直线与圆相切时, 取最值;
(Ⅱ)设x-2y=m,m表示一族平行直线在x轴上的截距,当直线x-2y=m与圆相切时,m 取最值. 例11 矩形ABCD的顶点A、B在直线y=2x+m上,C、D在抛物线y2=4x上,该矩形的外接圆方程为 x2+y2-x-4y-t=0 .
(Ⅰ)求矩形ABCD对角线交点M的坐标;
(Ⅱ)求此矩形边长,并确定m,t的值. 已知点A ( a,0 ) (a>0,a ≠1 ) 和 直 线 l :x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程的曲线类型与a 值的关系 .动点C到角两边距离相等动点C在AB上两个方程组成的参数方程引入参数b
