2.1.2空间中直线与直线之间的位置关系(2)[上学期]
文档属性
| 名称 | 2.1.2空间中直线与直线之间的位置关系(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 40.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-04 00:00:00 | ||
图片预览




文档简介
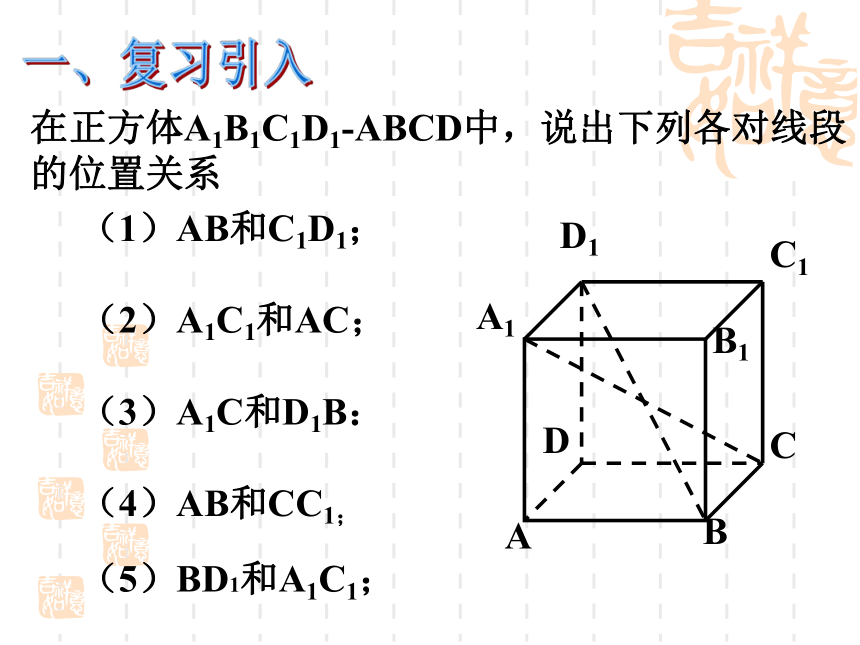
课件14张PPT。2.1.2空间中直线与直线之间的位置关系(2)问题:平面几何中,两条直线的位置关系:平行或相交在空间中是否还是如此呢?在正方体A1B1C1D1-ABCD中,说出下列各对线段的位置关系(1)AB和C1D1;
(2)A1C1和AC;
(3)A1C和D1B:
(4)AB和CC1;
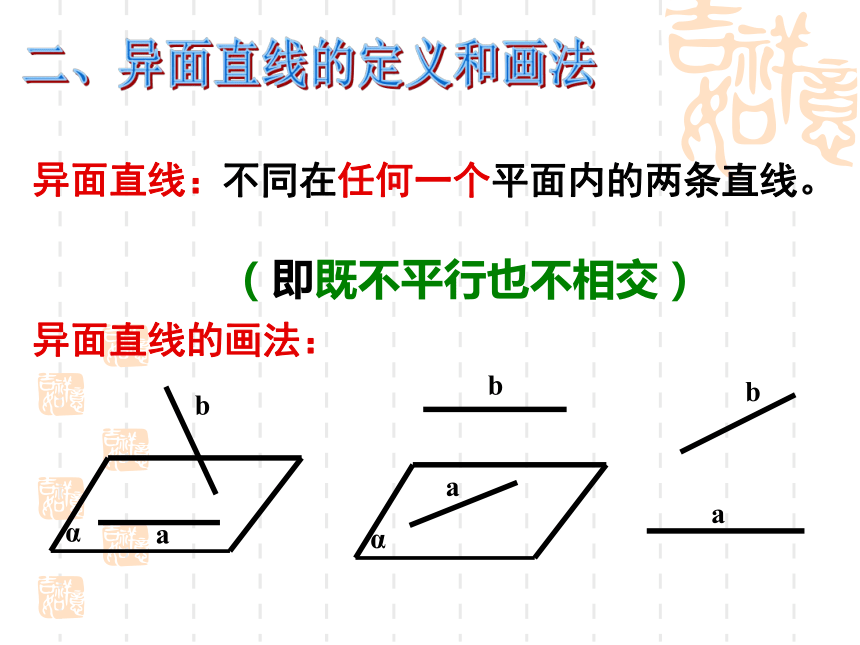
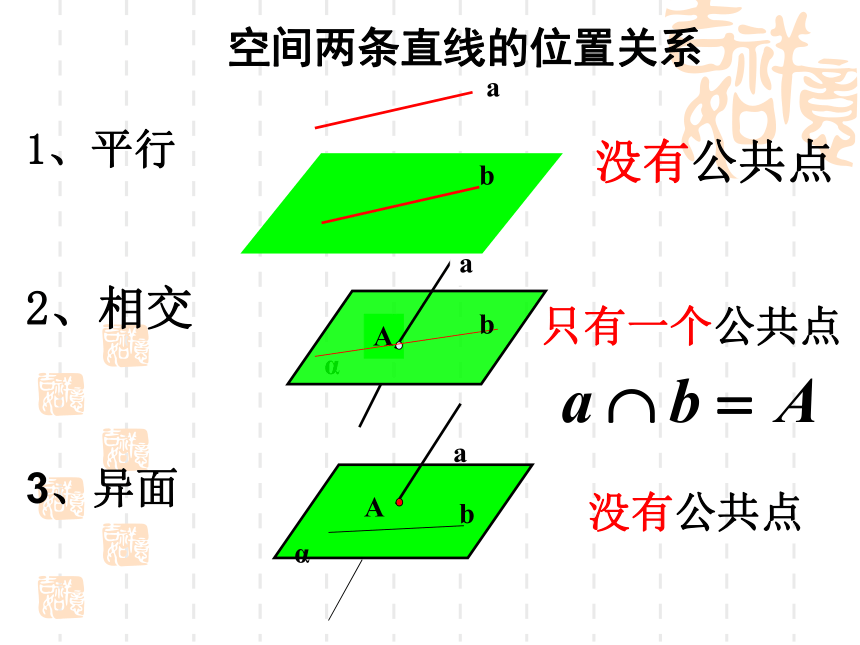
(5)BD1和A1C1;一、复习引入二、异面直线的定义和画法异面直线:不同在任何一个平面内的两条直线。(即既不平行也不相交)异面直线的画法: α Aa 空间两条直线的位置关系1、平行ab没有公共点2、相交bAα a3、异面没有公共点b只有一个公共点练习:判断下列说法的对错1、分别在两个平面内的两条直线一定是
异面直线;3、a与b是异面直线,b与c是异面直线,则a与c是异面直线;4、a与b是共面,b与c是共面,则a与c共面FFFF练习2:正方体ABCD-A1B1C1D11、与A1A是异面的有:2、与D1B异面的有:BC DC B1C1 D1C1AA1 AD A1B1 B1C1 CC1 CDP50 探究三、异面直线所成角的定义:1.直线a、b是异面直线。经过空间任意一点O,分
别引直线a1∥a,b1∥b。我们把直线a1和b1所成的
锐角(或直角)叫做异面直线a和b所成的角。b为了简便,点O常取在两条异面直线中的一条上。 2.异面直线a和b所成的角的范围:如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直。因此,异面直线所成角的范围是(0, ]3、特例:例1.如图,在正方体中,(1)哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小。
四、例题分析:解:(1)与直线BA1成异面直线有AD、CD、B1C1、C1D1、C1C、D1D(2)∵B1B∥C1C
∴∠A1B1B是异面直线BA1和CC1所成的角
易求得所成的角为例2.如图,正方体中,
A1B1与C1C所成的角
AD与B1B所成的角
A1D与BC1所成的角
D1C与A1A所成的角
A1D与AC所成的角
求异面直线所成的角的一般步骤是: 根据异面直线所成角的定义,求异面直线所成角,就是要将其变换成相交直线所成有角。其方法为: 平移法:即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角。(1)找出或作出有关的图形;
(2)证明它符合定义;
(3)计算。[即:要求先证,要证先作。] 具体地讲是选择“特殊点”作异面直线的平行线,构作含异面直线所成(或其补角)的角的三角形,再求之。1.空间两直线的位置关系:定义:不同在任何一个平面内的两条直线为异面直线小结:2.求异面直线所成的角的方法与步骤归纳为:①作辅助线找角;②指出角(或其补角);
③求角(解三角形);④结论。作业:学习辅导 P14 8、9
(2)A1C1和AC;
(3)A1C和D1B:
(4)AB和CC1;
(5)BD1和A1C1;一、复习引入二、异面直线的定义和画法异面直线:不同在任何一个平面内的两条直线。(即既不平行也不相交)异面直线的画法: α Aa 空间两条直线的位置关系1、平行ab没有公共点2、相交bAα a3、异面没有公共点b只有一个公共点练习:判断下列说法的对错1、分别在两个平面内的两条直线一定是
异面直线;3、a与b是异面直线,b与c是异面直线,则a与c是异面直线;4、a与b是共面,b与c是共面,则a与c共面FFFF练习2:正方体ABCD-A1B1C1D11、与A1A是异面的有:2、与D1B异面的有:BC DC B1C1 D1C1AA1 AD A1B1 B1C1 CC1 CDP50 探究三、异面直线所成角的定义:1.直线a、b是异面直线。经过空间任意一点O,分
别引直线a1∥a,b1∥b。我们把直线a1和b1所成的
锐角(或直角)叫做异面直线a和b所成的角。b为了简便,点O常取在两条异面直线中的一条上。 2.异面直线a和b所成的角的范围:如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直。因此,异面直线所成角的范围是(0, ]3、特例:例1.如图,在正方体中,(1)哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小。
四、例题分析:解:(1)与直线BA1成异面直线有AD、CD、B1C1、C1D1、C1C、D1D(2)∵B1B∥C1C
∴∠A1B1B是异面直线BA1和CC1所成的角
易求得所成的角为例2.如图,正方体中,
A1B1与C1C所成的角
AD与B1B所成的角
A1D与BC1所成的角
D1C与A1A所成的角
A1D与AC所成的角
求异面直线所成的角的一般步骤是: 根据异面直线所成角的定义,求异面直线所成角,就是要将其变换成相交直线所成有角。其方法为: 平移法:即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角。(1)找出或作出有关的图形;
(2)证明它符合定义;
(3)计算。[即:要求先证,要证先作。] 具体地讲是选择“特殊点”作异面直线的平行线,构作含异面直线所成(或其补角)的角的三角形,再求之。1.空间两直线的位置关系:定义:不同在任何一个平面内的两条直线为异面直线小结:2.求异面直线所成的角的方法与步骤归纳为:①作辅助线找角;②指出角(或其补角);
③求角(解三角形);④结论。作业:学习辅导 P14 8、9
