苏教版(2019)高中数学选择性必修第一册 1.3 两条直线的平行与垂直【同步精讲教案】(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第一册 1.3 两条直线的平行与垂直【同步精讲教案】(解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览




文档简介
第1章 直线与方程
第01讲 两条直线的平行与垂直
课程标准 重难点
1.理解并掌握两条直线平行的条件及两条直线垂直的条件;2.能根据已知条件判断两直线的平行与垂直;3.能应用两条直线平行或垂直进行实际应用. 1.直线的平行判断2.直线的垂直判断
知识点一 两条直线平行
1.对于两条不重合的直线l1,l2,其斜率分别为k1,k2,有l1∥l2 k1=k2.
【概念解读】对两直线平行与斜率的关系要注意以下几点
(1)l1∥l2 k1=k2成立的前提条件是:①两条直线的斜率都存在;②l1与l2不重合.
(2)当两条直线不重合且斜率都不存在时,l1与l2的倾斜角都是90°,则l1∥l2.
(3)两条不重合直线平行的判定的一般结论是:
l1∥l2 k1=k2或l1,l2斜率都不存在.
【知识拓展】
类型 斜率存在 斜率不存在
前提条件 α1=α2≠90° α1=α2=90°
对应关系 l1∥l2 k1=k2 l1∥l2 两直线斜率都不存在
图示
知识点二 两直线垂直
1.如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;反之,如果它们的斜率之积等于-1,那么它们互相垂直,即l1⊥l2 k1·k2=-1.
【概念解读】对两直线垂直与斜率的关系要注意以下几点
(1)l1⊥l2 k1·k2=-1成立的前提条件是:①两条直线的斜率都存在;②k1≠0且k2≠0.
(2)两条直线中,一条直线的斜率不存在,同时另一条直线的斜率等于零,则两条直线垂直.
(3)判定两条直线垂直的一般结论为:
l1⊥l2 k1·k2=-1或一条直线的斜率不存在,同时另一条直线的斜率等于零.
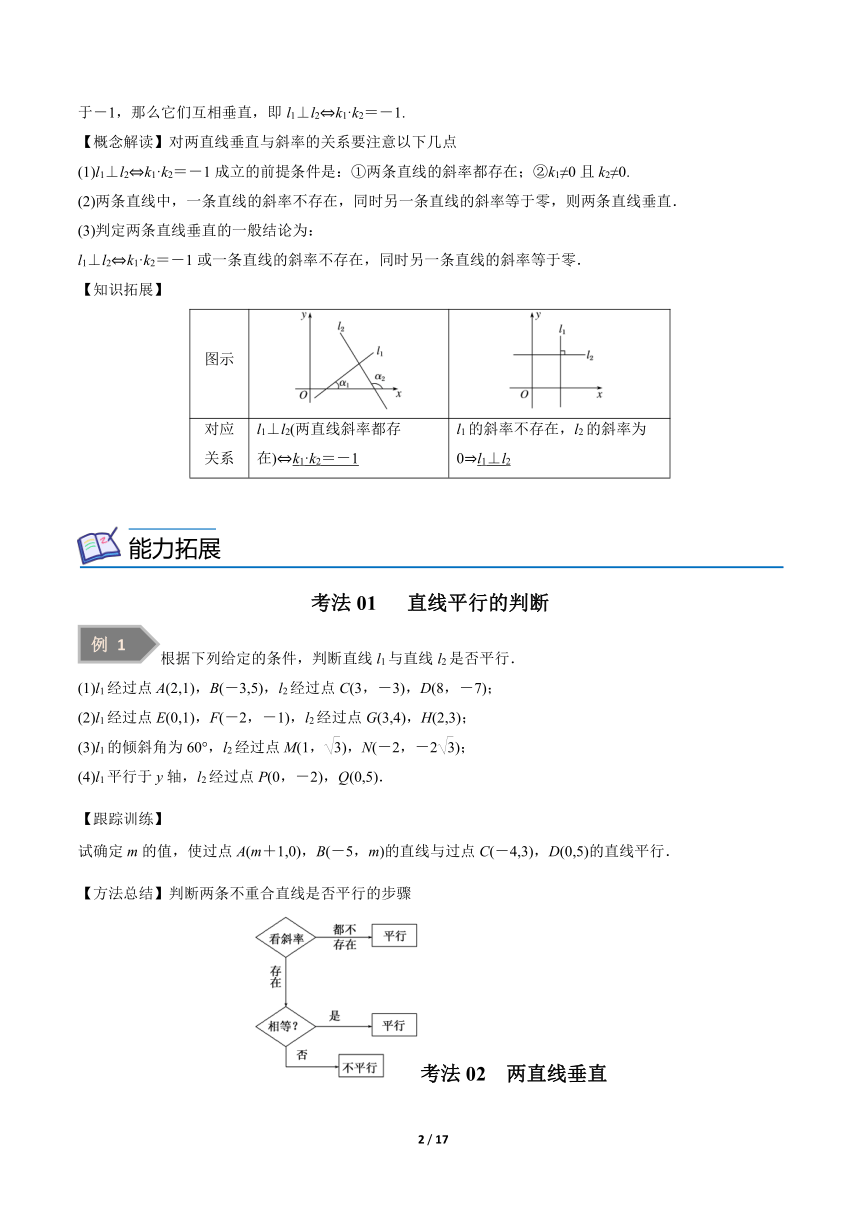
【知识拓展】
图示
对应关系 l1⊥l2(两直线斜率都存在) k1·k2=-1 l1的斜率不存在,l2的斜率为0 l1⊥l2
考法01 直线平行的判断
根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点A(2,1),B(-3,5),l2经过点C(3,-3),D(8,-7);
(2)l1经过点E(0,1),F(-2,-1),l2经过点G(3,4),H(2,3);
(3)l1的倾斜角为60°,l2经过点M(1,),N(-2,-2);
(4)l1平行于y轴,l2经过点P(0,-2),Q(0,5).
【跟踪训练】
试确定m的值,使过点A(m+1,0),B(-5,m)的直线与过点C(-4,3),D(0,5)的直线平行.
【方法总结】判断两条不重合直线是否平行的步骤
考法02 两直线垂直
已知两条直线l1,l2的斜率是方程3x2+mx-3=0(m∈R)的两个根,则l1与l2的位置关系是( )
A.平行 B.垂直
C.可能重合 D.无法确定
(1)直线x=0与直线y=0的位置关系是( )
A.垂直 B.平行 C.重合 D.以上都不对
【方法总结】
使用斜率公式判定两直线垂直的步骤
(1)一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第一步.
(2)二用:就是将点的坐标代入斜率公式.
(3)求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式要对参数进行讨论.
总之,l1与l2一个斜率为0,另一个斜率不存在时,l1⊥l2;l1与l2斜率都存在时,满足k1·k2=-1.
考法03 平行与垂直的综合运用
利用两直线的平行与垂直的判定,合理求解点的坐标,确定平面图形的面积,是两条直线平行与垂直的综合运用,是本节的重点,重在提升逻辑推理,数学运算的核心素养.
已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,则点D的坐标为 .
【素养变式】
本例中条件变为:已知矩形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),求第四个顶点D的坐标.
【素养达成】
已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A,B,C,D四点,试判定图形ABCD的形状.
题组A 基础过关练
1.已知直线:,:,且,则的值为( )
A. B. C.或 D.或
2.已知直线,.则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.巳知直线l1,l2的方程分别是l1 ∶mx+2y-4=0,l2;2x+y-8=0,若l1⊥l2,则m的值为( )
A.-1 B.2 C.3 D.4
4.已知直线与直线垂直,则a=( )
A.3 B.1或﹣3 C.﹣1 D.3或﹣1
5.直线:,:,则“”是“”的( )条件
A.必要不充分 B.充分不必要 C.充要 D.既不充分也不必要
6.已知m为实数,直线,,则“”是“”的_______条件.
7.直线与直线垂直,则为___________.
8.已知两条直线,,若,则的值为___________.
题组B 能力提升练
1.下列叙述中正确的是( )
A.命题“,”的否定是“,”
B.“”是“直线和直线垂直”的充分而不必要条件
C.命题“若,则且”的否命题是“若,则且”
D.若为真命题,为假命题,则,一真一假
2.直线,若,则的倾斜角是( )
A. B. C. D.
3.直线与直线平行,则的值为( )
A. B. C. D.
4.已知直线和互相平行,则( )
A. B. C.或 D.或
5.直线关于对称的直线方程是( )
A. B. C. D.
6.已知直线与平行,则的值为__________.
7.已知直线:与:互相垂直,其垂足为,则的值为________.
8.已知直线::,求实数m的值使得:
(1)相交;
(2);
(3)∥
题组C 培优拔尖练
1.已知分别是函数图象上不同的两点处的切线,分别与轴交于点,且与垂直相交于点,则的面积的取值范围是
A. B. C. D.
2.已知直线:,:互相垂直,则的取值范围为( )
A. B. C. D.
3.已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )
A.b=a3 B.b=a3+
C.(b-a3)=0 D.|b-a3|+=0
4.设a,b,c分别是△ABC的内角A,B,C所对的边,则直线sinA·x+ay-c=0与bx-sinB·y+sinC=0的位置关系是( )
A.平行 B.重合
C.垂直 D.相交但不垂直
5.,动直线过定点,动直线过定点,则点坐标为__________;若直线与相交于点(异于点,),则周长的最大值为__________.
6.设分别是△中的对边边长,则直线与直线的位置关系是_______________.
第1章 直线与方程答案
第01讲 两条直线的平行与垂直
课程标准 重难点
1.理解并掌握两条直线平行的条件及两条直线垂直的条件;2.能根据已知条件判断两直线的平行与垂直;3.能应用两条直线平行或垂直进行实际应用. 1.直线的平行判断2.直线的垂直判断
知识点一 两条直线平行
1.对于两条不重合的直线l1,l2,其斜率分别为k1,k2,有l1∥l2 k1=k2.
【概念解读】对两直线平行与斜率的关系要注意以下几点
(1)l1∥l2 k1=k2成立的前提条件是:①两条直线的斜率都存在;②l1与l2不重合.
(2)当两条直线不重合且斜率都不存在时,l1与l2的倾斜角都是90°,则l1∥l2.
(3)两条不重合直线平行的判定的一般结论是:
l1∥l2 k1=k2或l1,l2斜率都不存在.
【知识拓展】
类型 斜率存在 斜率不存在
前提条件 α1=α2≠90° α1=α2=90°
对应关系 l1∥l2 k1=k2 l1∥l2 两直线斜率都不存在
图示
知识点二 两直线垂直
1.如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;反之,如果它们的斜率之积等于-1,那么它们互相垂直,即l1⊥l2 k1·k2=-1.
【概念解读】对两直线垂直与斜率的关系要注意以下几点
(1)l1⊥l2 k1·k2=-1成立的前提条件是:①两条直线的斜率都存在;②k1≠0且k2≠0.
(2)两条直线中,一条直线的斜率不存在,同时另一条直线的斜率等于零,则两条直线垂直.
(3)判定两条直线垂直的一般结论为:
l1⊥l2 k1·k2=-1或一条直线的斜率不存在,同时另一条直线的斜率等于零.
【知识拓展】
图示
对应关系 l1⊥l2(两直线斜率都存在) k1·k2=-1 l1的斜率不存在,l2的斜率为0 l1⊥l2
考法01 直线平行的判断
根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点A(2,1),B(-3,5),l2经过点C(3,-3),D(8,-7);
(2)l1经过点E(0,1),F(-2,-1),l2经过点G(3,4),H(2,3);
(3)l1的倾斜角为60°,l2经过点M(1,),N(-2,-2);
(4)l1平行于y轴,l2经过点P(0,-2),Q(0,5).
【解析】(1)由题意知,k1==-,k2==-,所以直线l1与直线l2平行或重合,又kBC==-≠-,故l1∥l2.
(2)由题意知,k1==1,k2==1,所以直线l1与直线l2平行或重合,kFG==1,故直线l1与直线l2重合.
(3)由题意知,k1=tan 60°=,k2==,k1=k2,所以直线l1与直线l2平行或重合.
(4)由题意知l1的斜率不存在,且不是y轴,l2的斜率也不存在,恰好是y轴,所以l1∥l2.
【跟踪训练】
试确定m的值,使过点A(m+1,0),B(-5,m)的直线与过点C(-4,3),D(0,5)的直线平行.
【解析】由题意直线CD的斜率存在,则与其平行的直线AB的斜率也存在.kAB==,kCD==,由于AB∥CD,即kAB=kCD,所以=,得m=-2.经验证m=-2时直线AB的斜率存在,所以m=-2.
【方法总结】判断两条不重合直线是否平行的步骤
考法02 两直线垂直
已知两条直线l1,l2的斜率是方程3x2+mx-3=0(m∈R)的两个根,则l1与l2的位置关系是( )
A.平行 B.垂直
C.可能重合 D.无法确定
【答案】B
【解析】由方程3x2+mx-3=0知,Δ=m2-4×3×(-3)=m2+36>0恒成立.
故方程有两相异实根,即l1与l2的斜率k1,k2存在,设两根为x1,x2,则k1k2=x1x2=-1,故l1⊥l2,所以选B.
【即时训练】
(1)直线x=0与直线y=0的位置关系是( )
A.垂直 B.平行 C.重合 D.以上都不对
【答案】A
【解析】x=0是表示y轴的直线,y=0表示x轴的直线,两条直线互相垂直.故选A.
(2)已知直线l1:x+2y+1=0,l2:﹣2x+y+2=0,它们相交于点A.判断直线l1和l2是否垂直?请给出理由;
【解析】直线l1的斜率,直线l2的斜率k2=2,∵,∴l1⊥l2
【方法总结】
使用斜率公式判定两直线垂直的步骤
(1)一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第一步.
(2)二用:就是将点的坐标代入斜率公式.
(3)求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式要对参数进行讨论.
总之,l1与l2一个斜率为0,另一个斜率不存在时,l1⊥l2;l1与l2斜率都存在时,满足k1·k2=-1.
考法03 平行与垂直的综合运用
利用两直线的平行与垂直的判定,合理求解点的坐标,确定平面图形的面积,是两条直线平行与垂直的综合运用,是本节的重点,重在提升逻辑推理,数学运算的核心素养.
已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,则点D的坐标为 .
【解题思路】由题设条件知直线AB⊥CD,且AD∥BC,将此位置关系利用斜率关系转化为方程,即可求出点D的坐标
【答案】(10,﹣6)
【解析】设点D的坐标为(x,y),由已知得,直线AB的斜率KAB=1,(2分)
直线CD的斜率KCD=,直线CB的斜率KCB=,直线AD的斜率KAD=,
由AB⊥CD,且AD∥BC,得,解得,
所以D的坐标为:(10,﹣6).
【素养变式】
本例中条件变为:已知矩形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),求第四个顶点D的坐标.
【解析】设第四个顶点D的坐标为(x,y),因为AD⊥CD,AD∥BC,所以kAD·kCD=-1,且kAD=kBC.
所以解得
所以第四个顶点D的坐标为(2,3).
【素养达成】
已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A,B,C,D四点,试判定图形ABCD的形状.
【解析】由题意知A,B,C,D四点在坐标平面内的位置,如图所示,由斜率公式可得kAB==,
kCD==,kAD==-3,
kBC==-.
所以kAB=kCD,由图可知AB与CD不重合,
所以AB∥CD.由kAD≠kBC,所以AD与BC不平行.
又因为kAB·kAD=×(-3)=-1,
所以AB⊥AD,故四边形ABCD为直角梯形
题组A 基础过关练
1.已知直线:,:,且,则的值为( )
A. B. C.或 D.或
【答案】D
【解析】因为,所以,解得或.故选:D
2.已知直线,.则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【解析】由题意,直线,直线,
因为,可得,解得,
所以“”是“”的必要不充分条件.
故选:B.
3.巳知直线l1,l2的方程分别是l1 ∶mx+2y-4=0,l2;2x+y-8=0,若l1⊥l2,则m的值为( )
A.-1 B.2 C.3 D.4
【答案】A
【解析】因为,,
所以,
因为,所以
所以,解得故选:A
4.已知直线与直线垂直,则a=( )
A.3 B.1或﹣3 C.﹣1 D.3或﹣1
【答案】D
【解析】直线与直线垂直,
所以,解得或.
故选:D.
5.直线:,:,则“”是“”的( )条件
A.必要不充分 B.充分不必要 C.充要 D.既不充分也不必要
【答案】B
【解析】的充要条件是,解得或,
所以“”是“”的充分不必要条件.故选:B.
6.已知m为实数,直线,,则“”是“”的_______条件.
【答案】充分不必要
【解析】依题意,时,,从而有,解得或,
即命题的m取值集合为,而命题的m取值集合是,且有,
所以“”是“”的充分不必要条件.故答案为:充分不必要
7.直线与直线垂直,则为___________.
【答案】或
【解析】因为直线与直线垂直,
所以,解得或
故答案为:或
8.已知两条直线,,若,则的值为___________.
【答案】
【解析】当时,不满足,舍去;
当时,直线的斜率,的斜率
∵,
∴,
解得。故答案为:.
题组B 能力提升练
1.下列叙述中正确的是( )
A.命题“,”的否定是“,”
B.“”是“直线和直线垂直”的充分而不必要条件
C.命题“若,则且”的否命题是“若,则且”
D.若为真命题,为假命题,则,一真一假
【答案】D
【解析】选项:命题的否定为,,故选项错误;
选项:直线和直线垂直的充要条件为,即,可以推出,但推不出,故“”是“直线和直线垂直”的必要而不充分条件,故选项错误;
选项:命题“若,则且”的否命题是“若,则或”, 故选项错误;
选项:若为真命题,则,中至少有一个为真,若为假命题,则,中至少有一个为假,因此,一真一假,故选项正确.
故选:D.
2.直线,若,则的倾斜角是( )
A. B. C. D.
【答案】B
【解析】因为直线,
所以,
又,
所以的斜率为,
因为倾斜角的范围,
所以的倾斜角为,
故选:B
3.直线与直线平行,则的值为( )
A. B. C. D.
【答案】B
【解析】时,显然两直线不平行,
时,由两直线平行得,解得.
故选:B.
4.已知直线和互相平行,则( )
A. B. C.或 D.或
【答案】C
【解析】时,两直线显然不平行,时,则,解得或.故选:C.
5.直线关于对称的直线方程是( )
A. B. C. D.
【答案】A
【解析】设所求直线上任意一点是关于直线的对称点,
则,解得,
由对称性得在直线上,,
即,故选:A.
6.已知直线与平行,则的值为__________.
【答案】
【解析】由题得.
当时,两直线不重合.
故答案为:.
7.已知直线:与:互相垂直,其垂足为,则的值为________.
【答案】0
【解析】将直线,化为
直线,相互垂直,,解得
将代入,解得
将代入,解得
故答案为:
8.已知直线::,求实数m的值使得:
(1)相交;
(2);
(3)∥
【解析】(1)当和相交时,.
令,得,解得或.
所以当,且时,和相交.
(2)当时,,解得.
所以当时,.
(3)因为时,不平行于,
所以,所以,且,解得.
题组C 培优拔尖练
1.已知分别是函数图象上不同的两点处的切线,分别与轴交于点,且与垂直相交于点,则的面积的取值范围是
A. B. C. D.
【答案】A
【解析】由题意得.设,由导数的几何意义可得切线的斜率分别为,
由条件可得,所以,故.
又切线的方程为,切线的方程为,即
,在两切线方程中,分别令可得切线与y轴的交点分别为
,故.
由,可得点.
∴(由于,故等号不成立).
∴的面积的取值范围是.选A.
2.已知直线:,:互相垂直,则的取值范围为( )
A. B. C. D.
【答案】B
【解析】∵直线:,:互相垂直,
∴,∴,
∵,,∴.
∴的取值范围为.
故选:B.
3.已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )
A.b=a3 B.b=a3+
C.(b-a3)=0 D.|b-a3|+=0
【答案】C
【解析】若O为直角顶点,则B在x轴上,则a必为0,此时O,B重合,不符合题意;
若A为直角顶点,则b=a3≠0;
若B为直角顶点,根据斜率关系可知a2·=-1(a≠0),所以a(a3-b)=-1,即b-a3-=0;
以上两种情况皆有可能,所以必有(b-a3)=0成立.
故选:C
4.设a,b,c分别是△ABC的内角A,B,C所对的边,则直线sinA·x+ay-c=0与bx-sinB·y+sinC=0的位置关系是( )
A.平行 B.重合
C.垂直 D.相交但不垂直
【答案】C
【解析】直线sinA·x+ay-c=0的斜率,直线bx-sinB·y+sinC=0的斜率 ,故直线sinA·x+ay-c=0与直线bx-sinB·y+sinC=0垂直故选:C.
5.,动直线过定点,动直线过定点,则点坐标为__________;若直线与相交于点(异于点,),则周长的最大值为__________.
【答案】
【解析】由条件知直线过定点,直线过定点,所以,
又因为,所以,即,
所以,
当且仅当时取等号,所以,
故周长的最大值为
故答案为:①; ②.
6.设分别是△中的对边边长,则直线与直线的位置关系是_______________.
【解析】 分别是△内角 所对边的边,
故:,
的斜率为:
的斜率为:
根据正弦定理:
由
两条直线垂直
故答案为:垂直.
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
分层提分
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
分层提分
6 / 17
第01讲 两条直线的平行与垂直
课程标准 重难点
1.理解并掌握两条直线平行的条件及两条直线垂直的条件;2.能根据已知条件判断两直线的平行与垂直;3.能应用两条直线平行或垂直进行实际应用. 1.直线的平行判断2.直线的垂直判断
知识点一 两条直线平行
1.对于两条不重合的直线l1,l2,其斜率分别为k1,k2,有l1∥l2 k1=k2.
【概念解读】对两直线平行与斜率的关系要注意以下几点
(1)l1∥l2 k1=k2成立的前提条件是:①两条直线的斜率都存在;②l1与l2不重合.
(2)当两条直线不重合且斜率都不存在时,l1与l2的倾斜角都是90°,则l1∥l2.
(3)两条不重合直线平行的判定的一般结论是:
l1∥l2 k1=k2或l1,l2斜率都不存在.
【知识拓展】
类型 斜率存在 斜率不存在
前提条件 α1=α2≠90° α1=α2=90°
对应关系 l1∥l2 k1=k2 l1∥l2 两直线斜率都不存在
图示
知识点二 两直线垂直
1.如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;反之,如果它们的斜率之积等于-1,那么它们互相垂直,即l1⊥l2 k1·k2=-1.
【概念解读】对两直线垂直与斜率的关系要注意以下几点
(1)l1⊥l2 k1·k2=-1成立的前提条件是:①两条直线的斜率都存在;②k1≠0且k2≠0.
(2)两条直线中,一条直线的斜率不存在,同时另一条直线的斜率等于零,则两条直线垂直.
(3)判定两条直线垂直的一般结论为:
l1⊥l2 k1·k2=-1或一条直线的斜率不存在,同时另一条直线的斜率等于零.
【知识拓展】
图示
对应关系 l1⊥l2(两直线斜率都存在) k1·k2=-1 l1的斜率不存在,l2的斜率为0 l1⊥l2
考法01 直线平行的判断
根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点A(2,1),B(-3,5),l2经过点C(3,-3),D(8,-7);
(2)l1经过点E(0,1),F(-2,-1),l2经过点G(3,4),H(2,3);
(3)l1的倾斜角为60°,l2经过点M(1,),N(-2,-2);
(4)l1平行于y轴,l2经过点P(0,-2),Q(0,5).
【跟踪训练】
试确定m的值,使过点A(m+1,0),B(-5,m)的直线与过点C(-4,3),D(0,5)的直线平行.
【方法总结】判断两条不重合直线是否平行的步骤
考法02 两直线垂直
已知两条直线l1,l2的斜率是方程3x2+mx-3=0(m∈R)的两个根,则l1与l2的位置关系是( )
A.平行 B.垂直
C.可能重合 D.无法确定
(1)直线x=0与直线y=0的位置关系是( )
A.垂直 B.平行 C.重合 D.以上都不对
【方法总结】
使用斜率公式判定两直线垂直的步骤
(1)一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第一步.
(2)二用:就是将点的坐标代入斜率公式.
(3)求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式要对参数进行讨论.
总之,l1与l2一个斜率为0,另一个斜率不存在时,l1⊥l2;l1与l2斜率都存在时,满足k1·k2=-1.
考法03 平行与垂直的综合运用
利用两直线的平行与垂直的判定,合理求解点的坐标,确定平面图形的面积,是两条直线平行与垂直的综合运用,是本节的重点,重在提升逻辑推理,数学运算的核心素养.
已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,则点D的坐标为 .
【素养变式】
本例中条件变为:已知矩形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),求第四个顶点D的坐标.
【素养达成】
已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A,B,C,D四点,试判定图形ABCD的形状.
题组A 基础过关练
1.已知直线:,:,且,则的值为( )
A. B. C.或 D.或
2.已知直线,.则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.巳知直线l1,l2的方程分别是l1 ∶mx+2y-4=0,l2;2x+y-8=0,若l1⊥l2,则m的值为( )
A.-1 B.2 C.3 D.4
4.已知直线与直线垂直,则a=( )
A.3 B.1或﹣3 C.﹣1 D.3或﹣1
5.直线:,:,则“”是“”的( )条件
A.必要不充分 B.充分不必要 C.充要 D.既不充分也不必要
6.已知m为实数,直线,,则“”是“”的_______条件.
7.直线与直线垂直,则为___________.
8.已知两条直线,,若,则的值为___________.
题组B 能力提升练
1.下列叙述中正确的是( )
A.命题“,”的否定是“,”
B.“”是“直线和直线垂直”的充分而不必要条件
C.命题“若,则且”的否命题是“若,则且”
D.若为真命题,为假命题,则,一真一假
2.直线,若,则的倾斜角是( )
A. B. C. D.
3.直线与直线平行,则的值为( )
A. B. C. D.
4.已知直线和互相平行,则( )
A. B. C.或 D.或
5.直线关于对称的直线方程是( )
A. B. C. D.
6.已知直线与平行,则的值为__________.
7.已知直线:与:互相垂直,其垂足为,则的值为________.
8.已知直线::,求实数m的值使得:
(1)相交;
(2);
(3)∥
题组C 培优拔尖练
1.已知分别是函数图象上不同的两点处的切线,分别与轴交于点,且与垂直相交于点,则的面积的取值范围是
A. B. C. D.
2.已知直线:,:互相垂直,则的取值范围为( )
A. B. C. D.
3.已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )
A.b=a3 B.b=a3+
C.(b-a3)=0 D.|b-a3|+=0
4.设a,b,c分别是△ABC的内角A,B,C所对的边,则直线sinA·x+ay-c=0与bx-sinB·y+sinC=0的位置关系是( )
A.平行 B.重合
C.垂直 D.相交但不垂直
5.,动直线过定点,动直线过定点,则点坐标为__________;若直线与相交于点(异于点,),则周长的最大值为__________.
6.设分别是△中的对边边长,则直线与直线的位置关系是_______________.
第1章 直线与方程答案
第01讲 两条直线的平行与垂直
课程标准 重难点
1.理解并掌握两条直线平行的条件及两条直线垂直的条件;2.能根据已知条件判断两直线的平行与垂直;3.能应用两条直线平行或垂直进行实际应用. 1.直线的平行判断2.直线的垂直判断
知识点一 两条直线平行
1.对于两条不重合的直线l1,l2,其斜率分别为k1,k2,有l1∥l2 k1=k2.
【概念解读】对两直线平行与斜率的关系要注意以下几点
(1)l1∥l2 k1=k2成立的前提条件是:①两条直线的斜率都存在;②l1与l2不重合.
(2)当两条直线不重合且斜率都不存在时,l1与l2的倾斜角都是90°,则l1∥l2.
(3)两条不重合直线平行的判定的一般结论是:
l1∥l2 k1=k2或l1,l2斜率都不存在.
【知识拓展】
类型 斜率存在 斜率不存在
前提条件 α1=α2≠90° α1=α2=90°
对应关系 l1∥l2 k1=k2 l1∥l2 两直线斜率都不存在
图示
知识点二 两直线垂直
1.如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;反之,如果它们的斜率之积等于-1,那么它们互相垂直,即l1⊥l2 k1·k2=-1.
【概念解读】对两直线垂直与斜率的关系要注意以下几点
(1)l1⊥l2 k1·k2=-1成立的前提条件是:①两条直线的斜率都存在;②k1≠0且k2≠0.
(2)两条直线中,一条直线的斜率不存在,同时另一条直线的斜率等于零,则两条直线垂直.
(3)判定两条直线垂直的一般结论为:
l1⊥l2 k1·k2=-1或一条直线的斜率不存在,同时另一条直线的斜率等于零.
【知识拓展】
图示
对应关系 l1⊥l2(两直线斜率都存在) k1·k2=-1 l1的斜率不存在,l2的斜率为0 l1⊥l2
考法01 直线平行的判断
根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点A(2,1),B(-3,5),l2经过点C(3,-3),D(8,-7);
(2)l1经过点E(0,1),F(-2,-1),l2经过点G(3,4),H(2,3);
(3)l1的倾斜角为60°,l2经过点M(1,),N(-2,-2);
(4)l1平行于y轴,l2经过点P(0,-2),Q(0,5).
【解析】(1)由题意知,k1==-,k2==-,所以直线l1与直线l2平行或重合,又kBC==-≠-,故l1∥l2.
(2)由题意知,k1==1,k2==1,所以直线l1与直线l2平行或重合,kFG==1,故直线l1与直线l2重合.
(3)由题意知,k1=tan 60°=,k2==,k1=k2,所以直线l1与直线l2平行或重合.
(4)由题意知l1的斜率不存在,且不是y轴,l2的斜率也不存在,恰好是y轴,所以l1∥l2.
【跟踪训练】
试确定m的值,使过点A(m+1,0),B(-5,m)的直线与过点C(-4,3),D(0,5)的直线平行.
【解析】由题意直线CD的斜率存在,则与其平行的直线AB的斜率也存在.kAB==,kCD==,由于AB∥CD,即kAB=kCD,所以=,得m=-2.经验证m=-2时直线AB的斜率存在,所以m=-2.
【方法总结】判断两条不重合直线是否平行的步骤
考法02 两直线垂直
已知两条直线l1,l2的斜率是方程3x2+mx-3=0(m∈R)的两个根,则l1与l2的位置关系是( )
A.平行 B.垂直
C.可能重合 D.无法确定
【答案】B
【解析】由方程3x2+mx-3=0知,Δ=m2-4×3×(-3)=m2+36>0恒成立.
故方程有两相异实根,即l1与l2的斜率k1,k2存在,设两根为x1,x2,则k1k2=x1x2=-1,故l1⊥l2,所以选B.
【即时训练】
(1)直线x=0与直线y=0的位置关系是( )
A.垂直 B.平行 C.重合 D.以上都不对
【答案】A
【解析】x=0是表示y轴的直线,y=0表示x轴的直线,两条直线互相垂直.故选A.
(2)已知直线l1:x+2y+1=0,l2:﹣2x+y+2=0,它们相交于点A.判断直线l1和l2是否垂直?请给出理由;
【解析】直线l1的斜率,直线l2的斜率k2=2,∵,∴l1⊥l2
【方法总结】
使用斜率公式判定两直线垂直的步骤
(1)一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第一步.
(2)二用:就是将点的坐标代入斜率公式.
(3)求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式要对参数进行讨论.
总之,l1与l2一个斜率为0,另一个斜率不存在时,l1⊥l2;l1与l2斜率都存在时,满足k1·k2=-1.
考法03 平行与垂直的综合运用
利用两直线的平行与垂直的判定,合理求解点的坐标,确定平面图形的面积,是两条直线平行与垂直的综合运用,是本节的重点,重在提升逻辑推理,数学运算的核心素养.
已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,则点D的坐标为 .
【解题思路】由题设条件知直线AB⊥CD,且AD∥BC,将此位置关系利用斜率关系转化为方程,即可求出点D的坐标
【答案】(10,﹣6)
【解析】设点D的坐标为(x,y),由已知得,直线AB的斜率KAB=1,(2分)
直线CD的斜率KCD=,直线CB的斜率KCB=,直线AD的斜率KAD=,
由AB⊥CD,且AD∥BC,得,解得,
所以D的坐标为:(10,﹣6).
【素养变式】
本例中条件变为:已知矩形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),求第四个顶点D的坐标.
【解析】设第四个顶点D的坐标为(x,y),因为AD⊥CD,AD∥BC,所以kAD·kCD=-1,且kAD=kBC.
所以解得
所以第四个顶点D的坐标为(2,3).
【素养达成】
已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A,B,C,D四点,试判定图形ABCD的形状.
【解析】由题意知A,B,C,D四点在坐标平面内的位置,如图所示,由斜率公式可得kAB==,
kCD==,kAD==-3,
kBC==-.
所以kAB=kCD,由图可知AB与CD不重合,
所以AB∥CD.由kAD≠kBC,所以AD与BC不平行.
又因为kAB·kAD=×(-3)=-1,
所以AB⊥AD,故四边形ABCD为直角梯形
题组A 基础过关练
1.已知直线:,:,且,则的值为( )
A. B. C.或 D.或
【答案】D
【解析】因为,所以,解得或.故选:D
2.已知直线,.则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【解析】由题意,直线,直线,
因为,可得,解得,
所以“”是“”的必要不充分条件.
故选:B.
3.巳知直线l1,l2的方程分别是l1 ∶mx+2y-4=0,l2;2x+y-8=0,若l1⊥l2,则m的值为( )
A.-1 B.2 C.3 D.4
【答案】A
【解析】因为,,
所以,
因为,所以
所以,解得故选:A
4.已知直线与直线垂直,则a=( )
A.3 B.1或﹣3 C.﹣1 D.3或﹣1
【答案】D
【解析】直线与直线垂直,
所以,解得或.
故选:D.
5.直线:,:,则“”是“”的( )条件
A.必要不充分 B.充分不必要 C.充要 D.既不充分也不必要
【答案】B
【解析】的充要条件是,解得或,
所以“”是“”的充分不必要条件.故选:B.
6.已知m为实数,直线,,则“”是“”的_______条件.
【答案】充分不必要
【解析】依题意,时,,从而有,解得或,
即命题的m取值集合为,而命题的m取值集合是,且有,
所以“”是“”的充分不必要条件.故答案为:充分不必要
7.直线与直线垂直,则为___________.
【答案】或
【解析】因为直线与直线垂直,
所以,解得或
故答案为:或
8.已知两条直线,,若,则的值为___________.
【答案】
【解析】当时,不满足,舍去;
当时,直线的斜率,的斜率
∵,
∴,
解得。故答案为:.
题组B 能力提升练
1.下列叙述中正确的是( )
A.命题“,”的否定是“,”
B.“”是“直线和直线垂直”的充分而不必要条件
C.命题“若,则且”的否命题是“若,则且”
D.若为真命题,为假命题,则,一真一假
【答案】D
【解析】选项:命题的否定为,,故选项错误;
选项:直线和直线垂直的充要条件为,即,可以推出,但推不出,故“”是“直线和直线垂直”的必要而不充分条件,故选项错误;
选项:命题“若,则且”的否命题是“若,则或”, 故选项错误;
选项:若为真命题,则,中至少有一个为真,若为假命题,则,中至少有一个为假,因此,一真一假,故选项正确.
故选:D.
2.直线,若,则的倾斜角是( )
A. B. C. D.
【答案】B
【解析】因为直线,
所以,
又,
所以的斜率为,
因为倾斜角的范围,
所以的倾斜角为,
故选:B
3.直线与直线平行,则的值为( )
A. B. C. D.
【答案】B
【解析】时,显然两直线不平行,
时,由两直线平行得,解得.
故选:B.
4.已知直线和互相平行,则( )
A. B. C.或 D.或
【答案】C
【解析】时,两直线显然不平行,时,则,解得或.故选:C.
5.直线关于对称的直线方程是( )
A. B. C. D.
【答案】A
【解析】设所求直线上任意一点是关于直线的对称点,
则,解得,
由对称性得在直线上,,
即,故选:A.
6.已知直线与平行,则的值为__________.
【答案】
【解析】由题得.
当时,两直线不重合.
故答案为:.
7.已知直线:与:互相垂直,其垂足为,则的值为________.
【答案】0
【解析】将直线,化为
直线,相互垂直,,解得
将代入,解得
将代入,解得
故答案为:
8.已知直线::,求实数m的值使得:
(1)相交;
(2);
(3)∥
【解析】(1)当和相交时,.
令,得,解得或.
所以当,且时,和相交.
(2)当时,,解得.
所以当时,.
(3)因为时,不平行于,
所以,所以,且,解得.
题组C 培优拔尖练
1.已知分别是函数图象上不同的两点处的切线,分别与轴交于点,且与垂直相交于点,则的面积的取值范围是
A. B. C. D.
【答案】A
【解析】由题意得.设,由导数的几何意义可得切线的斜率分别为,
由条件可得,所以,故.
又切线的方程为,切线的方程为,即
,在两切线方程中,分别令可得切线与y轴的交点分别为
,故.
由,可得点.
∴(由于,故等号不成立).
∴的面积的取值范围是.选A.
2.已知直线:,:互相垂直,则的取值范围为( )
A. B. C. D.
【答案】B
【解析】∵直线:,:互相垂直,
∴,∴,
∵,,∴.
∴的取值范围为.
故选:B.
3.已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )
A.b=a3 B.b=a3+
C.(b-a3)=0 D.|b-a3|+=0
【答案】C
【解析】若O为直角顶点,则B在x轴上,则a必为0,此时O,B重合,不符合题意;
若A为直角顶点,则b=a3≠0;
若B为直角顶点,根据斜率关系可知a2·=-1(a≠0),所以a(a3-b)=-1,即b-a3-=0;
以上两种情况皆有可能,所以必有(b-a3)=0成立.
故选:C
4.设a,b,c分别是△ABC的内角A,B,C所对的边,则直线sinA·x+ay-c=0与bx-sinB·y+sinC=0的位置关系是( )
A.平行 B.重合
C.垂直 D.相交但不垂直
【答案】C
【解析】直线sinA·x+ay-c=0的斜率,直线bx-sinB·y+sinC=0的斜率 ,故直线sinA·x+ay-c=0与直线bx-sinB·y+sinC=0垂直故选:C.
5.,动直线过定点,动直线过定点,则点坐标为__________;若直线与相交于点(异于点,),则周长的最大值为__________.
【答案】
【解析】由条件知直线过定点,直线过定点,所以,
又因为,所以,即,
所以,
当且仅当时取等号,所以,
故周长的最大值为
故答案为:①; ②.
6.设分别是△中的对边边长,则直线与直线的位置关系是_______________.
【解析】 分别是△内角 所对边的边,
故:,
的斜率为:
的斜率为:
根据正弦定理:
由
两条直线垂直
故答案为:垂直.
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
分层提分
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
分层提分
6 / 17
