苏教版(2019)高中数学选择性必修第一册 1.3两条直线的平行与垂直(第1课时 两直线平行与垂直)【同步作业】(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第一册 1.3两条直线的平行与垂直(第1课时 两直线平行与垂直)【同步作业】(解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 411.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 19:23:48 | ||
图片预览




文档简介
1.2 两条直线的平行与垂直(第1课时 两直线平行与垂直)
一、单选题
1.(2020·贵州高二学业考试)已知直线,. 若,则的值为( )
A. B.0 C.2 D.4
2.(2021·全国高二专题练习)若两直线与平行,则的值为( )
A. B.2 C. D.0
3.(2021·全国高一课时练习)若方程表示平行于轴的直线,则的值是( )
A. B. C., D.1
4.(2021·全国高二课时练习)若直线l1,l2的倾斜角分别为α1,α2,且l1⊥l2,则有( )
A.α1-α2=90° B.α2-α1=90°
C.|α2-α1|=90° D.α1+α2=180°
5.(2021·浙江高二期末)下列直线中,与直线平行的是( )
A. B.
C. D.
6.(2021·全国高二专题练习)l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程为( )
A.x+2y-3=0 B.x-2y-3=0
C.2x-y-1=0 D.2x-y-3=0
7.(2020·全国高二课时练习)已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )
A.b=a3 B.b=a3+
C.(b-a3)=0 D.|b-a3|+=0
8.(2020·福建漳州市·龙海二中高二期中)点关于直线对称的点的坐标为( )
A. B. C. D.
二、多选题
9.(2020·全国高二单元测试)若,,,,下面结论中正确的是( )
A. B.
C. D.
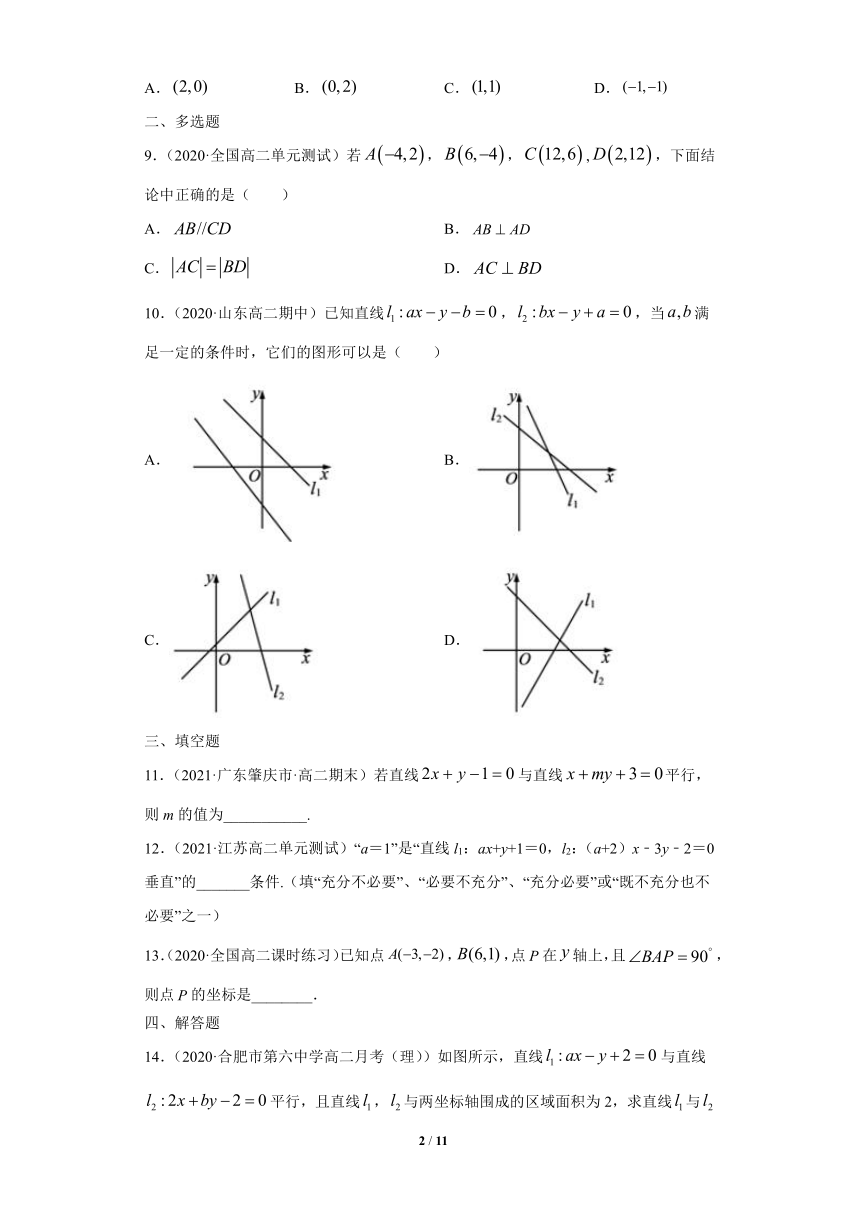
10.(2020·山东高二期中)已知直线,,当满足一定的条件时,它们的图形可以是( )
A. B.
C. D.
三、填空题
11.(2021·广东肇庆市·高二期末)若直线与直线平行,则m的值为___________.
12.(2021·江苏高二单元测试)“a=1”是“直线l1:ax+y+1=0,l2:(a+2)x﹣3y﹣2=0垂直”的_______条件.(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分也不必要”之一)
13.(2020·全国高二课时练习)已知点,,点在轴上,且,则点的坐标是________.
四、解答题
14.(2020·合肥市第六中学高二月考(理))如图所示,直线与直线平行,且直线,与两坐标轴围成的区域面积为2,求直线与的方程.
15.(2021·上海高二专题练习)当m为何值时,直线与直线.
(1)相交;
(2)垂直;
(3)平行;
(4)重合.
1.2 两条直线的平行与垂直(第1课时 两直线平行与垂直)答案
一、单选题
1.(2020·贵州高二学业考试)已知直线,. 若,则的值为( )
A. B.0 C.2 D.4
【答案】A
【分析】
由题意可得两直线斜率乘积为即可求解.
【详解】
直线的斜率为,直线的斜率为,
由题意可得:,解得:,
故选:A.
2.(2021·全国高二专题练习)若两直线与平行,则的值为( )
A. B.2 C. D.0
【答案】A
【分析】
根据两直线平行的充要条件可得,即可求的值.
【详解】
由题意知:,整理得,
∴,
故选:A
3.(2021·全国高一课时练习)若方程表示平行于轴的直线,则的值是( )
A. B. C., D.1
【答案】B
【分析】
根据直线与x轴平行,由直线方程各项系数的特征,即可求的值.
【详解】
直线与轴平行
∴,解得:
故选:B.
4.(2021·全国高二课时练习)若直线l1,l2的倾斜角分别为α1,α2,且l1⊥l2,则有( )
A.α1-α2=90° B.α2-α1=90°
C.|α2-α1|=90° D.α1+α2=180°
【答案】C
【分析】
利用直线垂直倾斜角关系直接求解
【详解】
两直线垂直,则它们的倾斜角的绝对值相差90°.
故选:C
5.(2021·浙江高二期末)下列直线中,与直线平行的是( )
A. B.
C. D.
【答案】B
【分析】
根据两直线的位置关系的判定方法,逐项判定,即可求解.
【详解】
对于A中,可得,根据两直线的位置关系,可得两直线重合,不符合题意;
对于B中,可得,根据两直线的位置关系,可得两直线平行,符合题意;
对于C中,可得,根据两直线的位置关系,可得两直线相交,不符合题意;
对于C中,可得,根据两直线的位置关系,可得两直线相交,不符合题意;
6.(2021·全国高二专题练习)l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程为( )
A.x+2y-3=0 B.x-2y-3=0
C.2x-y-1=0 D.2x-y-3=0
【答案】A
【分析】
根据题意,当两条平行直线与AB垂直时,两条平行直线的距离最大,求得直线l1的斜率,结合点斜式,即可求解.
【详解】
当两条平行直线与AB垂直时,两条平行直线的距离最大,
因为,所以
所以l1的方程为,即.
故选:A.
7.(2020·全国高二课时练习)已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )
A.b=a3 B.b=a3+
C.(b-a3)=0 D.|b-a3|+=0
【答案】C
【分析】
根据题意,分O为直角顶点、A为直角顶点、B为直角顶点三种情况,结合斜率关系分别求出满足的关系式即可求解.
【详解】
若O为直角顶点,则B在x轴上,则a必为0,此时O,B重合,不符合题意;
若A为直角顶点,则b=a3≠0;
若B为直角顶点,根据斜率关系可知a2·=-1(a≠0),所以a(a3-b)=-1,即b-a3-=0;
以上两种情况皆有可能,所以必有(b-a3)=0成立.
故选:C
8.(2020·福建漳州市·龙海二中高二期中)点关于直线对称的点的坐标为( )
A. B. C. D.
【答案】D
【分析】
点关于直线对称的点设为,由中点坐标公式和两直线垂直的条件:斜率之积为,解方程即可得到所求对称点坐标.
【详解】
设点关于直线对称的点坐标为,
可得
故选:D
二、多选题
9.(2020·全国高二单元测试)若,,,,下面结论中正确的是( )
A. B.
C. D.
【答案】ABCD
【分析】
分别计算,,,的斜率,根据斜率的关系判断A,B,D是否正确;然后利用两点间的距离公式计算和,判断D是否正确.
【详解】
因为,,且不在直线上,
所以,故A正确;
又因为,所以,所以,故B正确;
∵,,
∴,故C正确;
又,,
∴,∴,故D正确.
故选:ABCD.
10.(2020·山东高二期中)已知直线,,当满足一定的条件时,它们的图形可以是( )
A. B.
C. D.
【答案】AC
【分析】
首先将直线的一般式方程化为斜截式,根据斜率和截距之间的关系即可判断.
【详解】
解:直线可化为的斜率为,在轴上的截距为.
直线可化为,斜率为,在轴上的截距为.
当时,直线与平行,故正确.
选项中,由直线在轴上的截距可得,.
而由直线的斜率为,可得,故不正确.
在选项中,由直线的斜率为,而直线在轴上的截距.
直线在轴上的截距为,直线的斜率为,故正确.
选项中,两直线斜率,.
再由直线在轴上的截距,故不正确.
故选:.
三、填空题
11.(2021·广东肇庆市·高二期末)若直线与直线平行,则m的值为___________.
【答案】
【分析】
直接利用两直线平行,斜率相等,即可
【详解】
解析:∵直线与直线平行,∴斜率相等,即,∴.
故答案为: .
12.(2021·江苏高二单元测试)“a=1”是“直线l1:ax+y+1=0,l2:(a+2)x﹣3y﹣2=0垂直”的_______条件.(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分也不必要”之一)
【答案】充分不必要
【分析】
求出直线l1:ax+y+1=0,l2:(a+2)x﹣3y﹣2=0垂直对应的的取值范围即可判断.
【详解】
解:∵直线l1:ax+y+1=0和l2:(a+2)x﹣3y﹣2=0垂直,
∴a(a+2)﹣3=0,
解得a=﹣3,或a=1,
故实数“a=1”是“直线l1:ax+y+1=0,l2:(a+2)x﹣3y﹣2=0垂直的充分不必要条件.
故答案为:充分不必要.
13.(2020·全国高二课时练习)已知点,,点在轴上,且,则点的坐标是________.
【答案】
【分析】
设,由,利用坐标运算即可得解.
【详解】
设,由题意知,,存在,
又知,所以,解得.
所以点的坐标是.
故答案为:.
四、解答题
14.(2020·合肥市第六中学高二月考(理))如图所示,直线与直线平行,且直线,与两坐标轴围成的区域面积为2,求直线与的方程.
【答案】直线的方程为,直线的方程为.
【分析】
由图象可知,再由直线,与两坐标轴围成的区域面积为2得 可得答案.
【详解】
由图象可知,,
∵与平行,∴,
∵直线,与两坐标轴围成的区域面积为2,
∴,即,∴,
又,∴,即代入得,
∴,,
故直线的方程为,直线的方程为.
15.(2021·上海高二专题练习)当m为何值时,直线与直线.
(1)相交;
(2)垂直;
(3)平行;
(4)重合.
【答案】(1)且;(2);(3);(4).
【分析】
若两直线,(1)由相交,有;(2)由垂直,有;(3)(4)由平行或重合,有;根据以上不同情况列方程求m的值.
【详解】
(1)两线相交,则,即,得且;
(2)两线垂直,则,即,得;
(3)两线平行,则,即,得且,
当时,两直线方程均为为同一直线,不合题意;
当时,直线方程分别为、.
∴.
(4)由(3)知:两线重合,有.
2 / 2
一、单选题
1.(2020·贵州高二学业考试)已知直线,. 若,则的值为( )
A. B.0 C.2 D.4
2.(2021·全国高二专题练习)若两直线与平行,则的值为( )
A. B.2 C. D.0
3.(2021·全国高一课时练习)若方程表示平行于轴的直线,则的值是( )
A. B. C., D.1
4.(2021·全国高二课时练习)若直线l1,l2的倾斜角分别为α1,α2,且l1⊥l2,则有( )
A.α1-α2=90° B.α2-α1=90°
C.|α2-α1|=90° D.α1+α2=180°
5.(2021·浙江高二期末)下列直线中,与直线平行的是( )
A. B.
C. D.
6.(2021·全国高二专题练习)l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程为( )
A.x+2y-3=0 B.x-2y-3=0
C.2x-y-1=0 D.2x-y-3=0
7.(2020·全国高二课时练习)已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )
A.b=a3 B.b=a3+
C.(b-a3)=0 D.|b-a3|+=0
8.(2020·福建漳州市·龙海二中高二期中)点关于直线对称的点的坐标为( )
A. B. C. D.
二、多选题
9.(2020·全国高二单元测试)若,,,,下面结论中正确的是( )
A. B.
C. D.
10.(2020·山东高二期中)已知直线,,当满足一定的条件时,它们的图形可以是( )
A. B.
C. D.
三、填空题
11.(2021·广东肇庆市·高二期末)若直线与直线平行,则m的值为___________.
12.(2021·江苏高二单元测试)“a=1”是“直线l1:ax+y+1=0,l2:(a+2)x﹣3y﹣2=0垂直”的_______条件.(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分也不必要”之一)
13.(2020·全国高二课时练习)已知点,,点在轴上,且,则点的坐标是________.
四、解答题
14.(2020·合肥市第六中学高二月考(理))如图所示,直线与直线平行,且直线,与两坐标轴围成的区域面积为2,求直线与的方程.
15.(2021·上海高二专题练习)当m为何值时,直线与直线.
(1)相交;
(2)垂直;
(3)平行;
(4)重合.
1.2 两条直线的平行与垂直(第1课时 两直线平行与垂直)答案
一、单选题
1.(2020·贵州高二学业考试)已知直线,. 若,则的值为( )
A. B.0 C.2 D.4
【答案】A
【分析】
由题意可得两直线斜率乘积为即可求解.
【详解】
直线的斜率为,直线的斜率为,
由题意可得:,解得:,
故选:A.
2.(2021·全国高二专题练习)若两直线与平行,则的值为( )
A. B.2 C. D.0
【答案】A
【分析】
根据两直线平行的充要条件可得,即可求的值.
【详解】
由题意知:,整理得,
∴,
故选:A
3.(2021·全国高一课时练习)若方程表示平行于轴的直线,则的值是( )
A. B. C., D.1
【答案】B
【分析】
根据直线与x轴平行,由直线方程各项系数的特征,即可求的值.
【详解】
直线与轴平行
∴,解得:
故选:B.
4.(2021·全国高二课时练习)若直线l1,l2的倾斜角分别为α1,α2,且l1⊥l2,则有( )
A.α1-α2=90° B.α2-α1=90°
C.|α2-α1|=90° D.α1+α2=180°
【答案】C
【分析】
利用直线垂直倾斜角关系直接求解
【详解】
两直线垂直,则它们的倾斜角的绝对值相差90°.
故选:C
5.(2021·浙江高二期末)下列直线中,与直线平行的是( )
A. B.
C. D.
【答案】B
【分析】
根据两直线的位置关系的判定方法,逐项判定,即可求解.
【详解】
对于A中,可得,根据两直线的位置关系,可得两直线重合,不符合题意;
对于B中,可得,根据两直线的位置关系,可得两直线平行,符合题意;
对于C中,可得,根据两直线的位置关系,可得两直线相交,不符合题意;
对于C中,可得,根据两直线的位置关系,可得两直线相交,不符合题意;
6.(2021·全国高二专题练习)l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程为( )
A.x+2y-3=0 B.x-2y-3=0
C.2x-y-1=0 D.2x-y-3=0
【答案】A
【分析】
根据题意,当两条平行直线与AB垂直时,两条平行直线的距离最大,求得直线l1的斜率,结合点斜式,即可求解.
【详解】
当两条平行直线与AB垂直时,两条平行直线的距离最大,
因为,所以
所以l1的方程为,即.
故选:A.
7.(2020·全国高二课时练习)已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )
A.b=a3 B.b=a3+
C.(b-a3)=0 D.|b-a3|+=0
【答案】C
【分析】
根据题意,分O为直角顶点、A为直角顶点、B为直角顶点三种情况,结合斜率关系分别求出满足的关系式即可求解.
【详解】
若O为直角顶点,则B在x轴上,则a必为0,此时O,B重合,不符合题意;
若A为直角顶点,则b=a3≠0;
若B为直角顶点,根据斜率关系可知a2·=-1(a≠0),所以a(a3-b)=-1,即b-a3-=0;
以上两种情况皆有可能,所以必有(b-a3)=0成立.
故选:C
8.(2020·福建漳州市·龙海二中高二期中)点关于直线对称的点的坐标为( )
A. B. C. D.
【答案】D
【分析】
点关于直线对称的点设为,由中点坐标公式和两直线垂直的条件:斜率之积为,解方程即可得到所求对称点坐标.
【详解】
设点关于直线对称的点坐标为,
可得
故选:D
二、多选题
9.(2020·全国高二单元测试)若,,,,下面结论中正确的是( )
A. B.
C. D.
【答案】ABCD
【分析】
分别计算,,,的斜率,根据斜率的关系判断A,B,D是否正确;然后利用两点间的距离公式计算和,判断D是否正确.
【详解】
因为,,且不在直线上,
所以,故A正确;
又因为,所以,所以,故B正确;
∵,,
∴,故C正确;
又,,
∴,∴,故D正确.
故选:ABCD.
10.(2020·山东高二期中)已知直线,,当满足一定的条件时,它们的图形可以是( )
A. B.
C. D.
【答案】AC
【分析】
首先将直线的一般式方程化为斜截式,根据斜率和截距之间的关系即可判断.
【详解】
解:直线可化为的斜率为,在轴上的截距为.
直线可化为,斜率为,在轴上的截距为.
当时,直线与平行,故正确.
选项中,由直线在轴上的截距可得,.
而由直线的斜率为,可得,故不正确.
在选项中,由直线的斜率为,而直线在轴上的截距.
直线在轴上的截距为,直线的斜率为,故正确.
选项中,两直线斜率,.
再由直线在轴上的截距,故不正确.
故选:.
三、填空题
11.(2021·广东肇庆市·高二期末)若直线与直线平行,则m的值为___________.
【答案】
【分析】
直接利用两直线平行,斜率相等,即可
【详解】
解析:∵直线与直线平行,∴斜率相等,即,∴.
故答案为: .
12.(2021·江苏高二单元测试)“a=1”是“直线l1:ax+y+1=0,l2:(a+2)x﹣3y﹣2=0垂直”的_______条件.(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分也不必要”之一)
【答案】充分不必要
【分析】
求出直线l1:ax+y+1=0,l2:(a+2)x﹣3y﹣2=0垂直对应的的取值范围即可判断.
【详解】
解:∵直线l1:ax+y+1=0和l2:(a+2)x﹣3y﹣2=0垂直,
∴a(a+2)﹣3=0,
解得a=﹣3,或a=1,
故实数“a=1”是“直线l1:ax+y+1=0,l2:(a+2)x﹣3y﹣2=0垂直的充分不必要条件.
故答案为:充分不必要.
13.(2020·全国高二课时练习)已知点,,点在轴上,且,则点的坐标是________.
【答案】
【分析】
设,由,利用坐标运算即可得解.
【详解】
设,由题意知,,存在,
又知,所以,解得.
所以点的坐标是.
故答案为:.
四、解答题
14.(2020·合肥市第六中学高二月考(理))如图所示,直线与直线平行,且直线,与两坐标轴围成的区域面积为2,求直线与的方程.
【答案】直线的方程为,直线的方程为.
【分析】
由图象可知,再由直线,与两坐标轴围成的区域面积为2得 可得答案.
【详解】
由图象可知,,
∵与平行,∴,
∵直线,与两坐标轴围成的区域面积为2,
∴,即,∴,
又,∴,即代入得,
∴,,
故直线的方程为,直线的方程为.
15.(2021·上海高二专题练习)当m为何值时,直线与直线.
(1)相交;
(2)垂直;
(3)平行;
(4)重合.
【答案】(1)且;(2);(3);(4).
【分析】
若两直线,(1)由相交,有;(2)由垂直,有;(3)(4)由平行或重合,有;根据以上不同情况列方程求m的值.
【详解】
(1)两线相交,则,即,得且;
(2)两线垂直,则,即,得;
(3)两线平行,则,即,得且,
当时,两直线方程均为为同一直线,不合题意;
当时,直线方程分别为、.
∴.
(4)由(3)知:两线重合,有.
2 / 2
