4.3.2 角的比较与运算 课件(共31张PPT)
文档属性
| 名称 | 4.3.2 角的比较与运算 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 06:55:12 | ||
图片预览





文档简介
(共31张PPT)
人教版七上第四章几何图形初步
4.3.2角的比较与运算
人教版七年级上册
教学目标
1.会比较两个角的大小,及和差关系.
2.学会借助三角板拼出不同度数的角,提高学生的动手操作的能力.
3.认识角的平分线及角的等分线.
教学重点:
比较角的大小,分析角的和差关系.
教学难点:
角的和差关系及角平分线相合综合运用.
复习回顾
1. 角的定义①(静态的):有公共端点的两条射线组成的图形叫做角.
②(动态的):角可以看成是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形.
2.角的表示方法:
(1).大写英文字母
(2).数字
(3).小写希腊字母
3.角的换算:1周角=360°,1平角=180°,
1°=60', 1'=60", 1°=3600".
新知导入
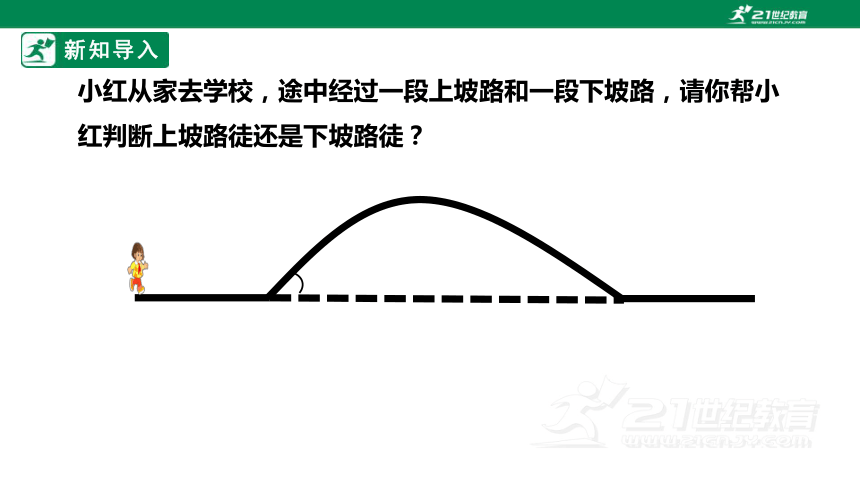
小红从家去学校,途中经过一段上坡路和一段下坡路,请你帮小红判断上坡路徒还是下坡路徒?
新知讲解
一.角的大小比较
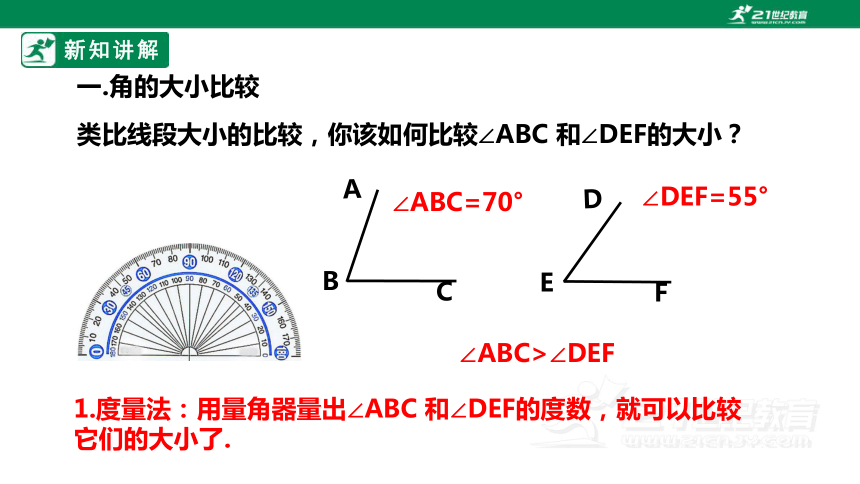
类比线段大小的比较,你该如何比较∠ABC 和∠DEF的大小?
B
C
A
E
F
D
∠ABC=70°
∠DEF=55°
∠ABC>∠DEF
1.度量法:用量角器量出∠ABC 和∠DEF的度数,就可以比较它们的大小了.
新知讲解
B
A
C
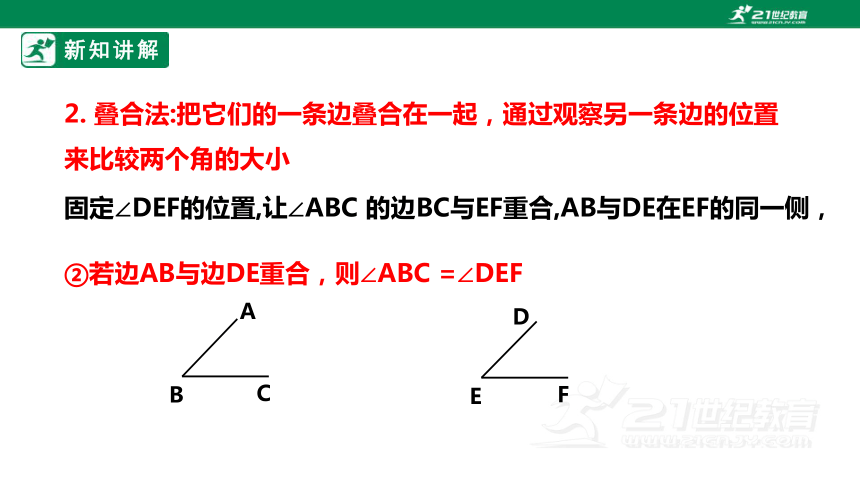
2. 叠合法:把它们的一条边叠合在一起,通过观察另一条边的位置来比较两个角的大小
除了度量法,还有什么方法比较∠ABC 和∠DEF的大小?
固定∠DEF的位置,让∠ABC 的边BC与EF重合,AB与DE在EF的同一侧,
E
D
F
①若边AB在∠DEF内部,则∠ABC <∠DEF
新知讲解
B
A
C
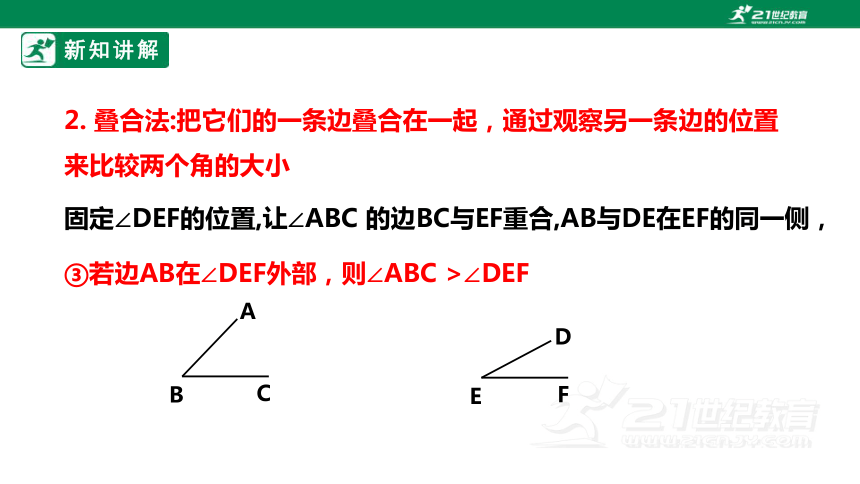
2. 叠合法:把它们的一条边叠合在一起,通过观察另一条边的位置来比较两个角的大小
固定∠DEF的位置,让∠ABC 的边BC与EF重合,AB与DE在EF的同一侧,
E
D
F
②若边AB与边DE重合,则∠ABC =∠DEF
新知讲解
B
A
C
2. 叠合法:把它们的一条边叠合在一起,通过观察另一条边的位置来比较两个角的大小
固定∠DEF的位置,让∠ABC 的边BC与EF重合,AB与DE在EF的同一侧,
E
D
F
③若边AB在∠DEF外部,则∠ABC >∠DEF
新知讲解
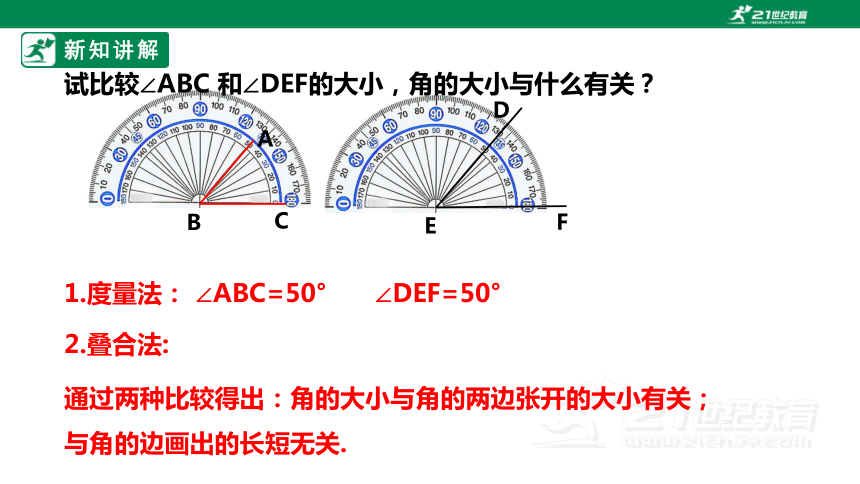
试比较∠ABC 和∠DEF的大小,角的大小与什么有关?
B
A
C
E
D
F
∠ABC=50°
∠DEF=50°
1.度量法:
2.叠合法:
通过两种比较得出:角的大小与角的两边张开的大小有关;
与角的边画出的长短无关.
新知讲解
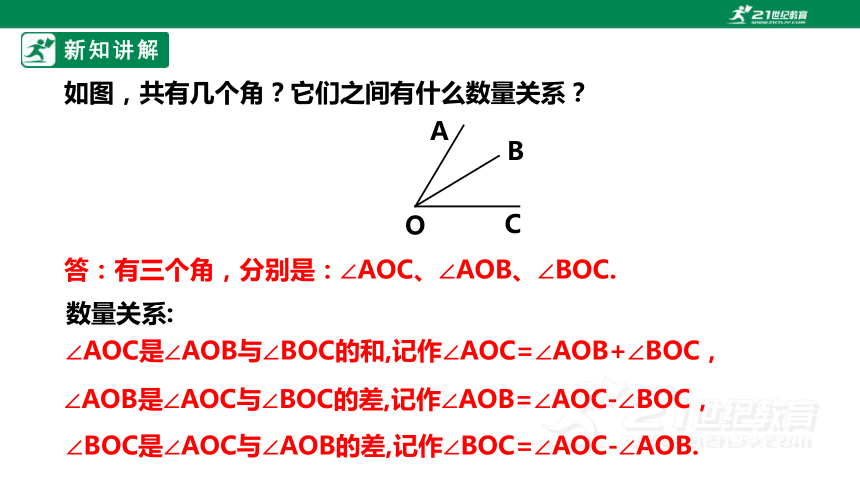
如图,共有几个角?它们之间有什么数量关系?
O
B
C
A
答:有三个角,分别是:∠AOC、∠AOB、∠BOC.
∠BOC是∠AOC与∠AOB的差,记作∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与∠BOC的和,记作∠AOC=∠AOB+∠BOC,
∠AOB是∠AOC与∠BOC的差,记作∠AOB=∠AOC-∠BOC,
数量关系:
练一练
如图,填空:
(3). ∠BOC=∠AOB- .
(1).∠AOB= +∠BOC,
(2). ∠AOB=∠AOD+ +∠BOC,
O
B
C
A
D
(4). ∠COD=∠AOB- - .
∠AOB
∠AOC
∠COD
∠AOD
∠COB
新知讲解
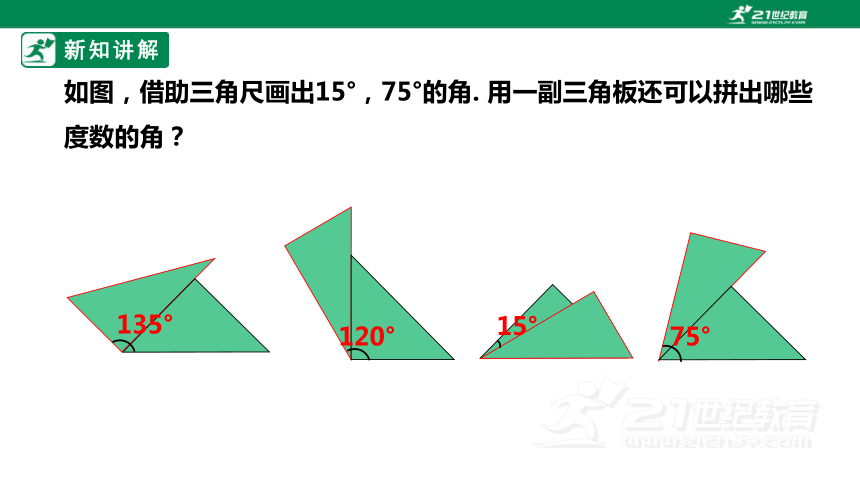
如图,借助三角尺画出15°,75°的角. 用一副三角板还可以拼出哪些度数的角?
135°
120°
15°
75°
新知讲解
如图,借助三角尺画出15°,75°的角. 用一副三角板还可以拼出哪些度数的角?
105°
150°
180°
新知讲解
如图,借助三角尺拼出15°,75°的角. 用一副三角板还可以拼出哪些度数的角?
45°
30°
60°
一共可以拼出的角度有15° 、30°、 45°、 60° 、75° 105° 、120°、 135° 、150° 、180° .
实际上凡是15°的整数倍的角,都可以用三角尺画出.
新知讲解
我们知道,线段的中点把线段分成相等的两条线段.类似地,如图,如果∠AOB=∠BOC,那么射线OB把∠AOC分成两个相等的角.
o
A
C
B
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .
∠BOC
∠AOC
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
射线OB叫做∠AOC的角平分线
新知讲解
α
α
α
A
B
C
D
O
类似地,还有角的三等分线等……
OB、OC是∠AOD的三等分线.
新知讲解
例1 如图O是直线AB上一点,∠AOC=53 17′,求∠BOC的度数.
分析:AB是直线,∠AOB是平角, ∠BOC 和∠AOC的和等于∠AOB.
解:由题意可知, ∠AOB是平角, ∠AOB =∠BOC+∠AOC.
∴ ∠BOC =∠AOB -∠AOC
=180 - 53 17′
=126 43′
o
A
C
B
新知讲解
例2.把一个周角分为7等分,每一份是多少度?(精确到分)
解: 360o÷7
=51o+3o÷7
=51o+180’ ÷7
≈ 51o26’
答:每一份是51°26’的角.
新知讲解
例3计算:
(1);
(2). .
(3).
=17°38'41''
=46°76'94''-29°38'53''
(1)解:47°17'34''-29°38'53''
(2).
=70°45'-17°57'10''
=52°47'50''
新知讲解
(3)
=(33°+24°)+(16'+46')+(28''+37'')
=57°+1°2'+1'5''
=58°3'5''.
用度、分、秒分别相减,注意度、分、秒之间的进制都是60进制,小单位不够减,需要向上一级单位借1.
度、分、秒之间的进制都是60进制,小单位满60需要向上一级单位进1.
新知讲解
例4 如图所示,OE是∠AOB的平分线,OD是∠BOC的平分线,∠AOB=100°,∠EOD=80°,求∠BOC的度数.
解:∵OE是∠AOB的平分线,∠AOB=100°,
∴∠BOE= ∠AOB=50°.
∵∠BOE+∠BOD=∠EOD=80°,
∴∠BOD=∠EOD﹣∠BOE=80°﹣50°=30°.
∵OD是∠BOC的平分线,
∴∠BOC=2∠BOD=60°.
答:∠BOC的度数60°.
课堂练习
1.在同一平面内,已知 , , 则等于( ).
A. 80° B. 40°
C. 80°或40° D. 20°
2.只利用一副学生用的三角尺可以画出的角度为( ).
A. 50° B. 105° C. 35° D. 125°
C
B
课堂练习
3.如图所示,若∠AOB=∠COD , 那么( )
∠1>∠2 B. ∠1=∠2
C. ∠1<∠2 D. 无法比较
4. 已知:∠ 1= ,∠ 2 ,∠ 3= ,则下列说法正确的是( )
∠1=∠2 B. ∠2=∠3
C. ∠1=∠3 D. ∠1、∠2、∠3互不相等
B
C
课堂练习
5. 计算:
(1) .
(2) .
(3) .
(4) .
解:(1)
(2)
=110°90′
=111°30′
课堂练习
(3)
(4)
课堂练习
6. 如图, , , , 平分 ,求 的度数.
解:∵∠AOB=37°,∠BOC=45°,∠COD=40°,
∴∠AOD=122°,
∵OE平分∠AOD,
∴∠AOE= ×122°=61°,
∴∠BOE=∠AOE-∠AOB=61°-37°=24°
A
B
C
D
O
E
课堂练习
∴∠BOM=35°+110°=145°.
7. 如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=70°,求∠BOM的值.
解:∵∠BOD=70°,
∴∠AOC=70°,∠COB=110°,
∵射线OM是∠AOC的平分线,
∴∠COM=35°,
A
B
C
D
O
M
课堂总结
一.角的大小比较
1.度量法:
2.叠合法:
二.角的和差关系
三.角的平分线
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
作业布置
习题4.3
第139页第6题
第140页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版七上第四章几何图形初步
4.3.2角的比较与运算
人教版七年级上册
教学目标
1.会比较两个角的大小,及和差关系.
2.学会借助三角板拼出不同度数的角,提高学生的动手操作的能力.
3.认识角的平分线及角的等分线.
教学重点:
比较角的大小,分析角的和差关系.
教学难点:
角的和差关系及角平分线相合综合运用.
复习回顾
1. 角的定义①(静态的):有公共端点的两条射线组成的图形叫做角.
②(动态的):角可以看成是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形.
2.角的表示方法:
(1).大写英文字母
(2).数字
(3).小写希腊字母
3.角的换算:1周角=360°,1平角=180°,
1°=60', 1'=60", 1°=3600".
新知导入
小红从家去学校,途中经过一段上坡路和一段下坡路,请你帮小红判断上坡路徒还是下坡路徒?
新知讲解
一.角的大小比较
类比线段大小的比较,你该如何比较∠ABC 和∠DEF的大小?
B
C
A
E
F
D
∠ABC=70°
∠DEF=55°
∠ABC>∠DEF
1.度量法:用量角器量出∠ABC 和∠DEF的度数,就可以比较它们的大小了.
新知讲解
B
A
C
2. 叠合法:把它们的一条边叠合在一起,通过观察另一条边的位置来比较两个角的大小
除了度量法,还有什么方法比较∠ABC 和∠DEF的大小?
固定∠DEF的位置,让∠ABC 的边BC与EF重合,AB与DE在EF的同一侧,
E
D
F
①若边AB在∠DEF内部,则∠ABC <∠DEF
新知讲解
B
A
C
2. 叠合法:把它们的一条边叠合在一起,通过观察另一条边的位置来比较两个角的大小
固定∠DEF的位置,让∠ABC 的边BC与EF重合,AB与DE在EF的同一侧,
E
D
F
②若边AB与边DE重合,则∠ABC =∠DEF
新知讲解
B
A
C
2. 叠合法:把它们的一条边叠合在一起,通过观察另一条边的位置来比较两个角的大小
固定∠DEF的位置,让∠ABC 的边BC与EF重合,AB与DE在EF的同一侧,
E
D
F
③若边AB在∠DEF外部,则∠ABC >∠DEF
新知讲解
试比较∠ABC 和∠DEF的大小,角的大小与什么有关?
B
A
C
E
D
F
∠ABC=50°
∠DEF=50°
1.度量法:
2.叠合法:
通过两种比较得出:角的大小与角的两边张开的大小有关;
与角的边画出的长短无关.
新知讲解
如图,共有几个角?它们之间有什么数量关系?
O
B
C
A
答:有三个角,分别是:∠AOC、∠AOB、∠BOC.
∠BOC是∠AOC与∠AOB的差,记作∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与∠BOC的和,记作∠AOC=∠AOB+∠BOC,
∠AOB是∠AOC与∠BOC的差,记作∠AOB=∠AOC-∠BOC,
数量关系:
练一练
如图,填空:
(3). ∠BOC=∠AOB- .
(1).∠AOB= +∠BOC,
(2). ∠AOB=∠AOD+ +∠BOC,
O
B
C
A
D
(4). ∠COD=∠AOB- - .
∠AOB
∠AOC
∠COD
∠AOD
∠COB
新知讲解
如图,借助三角尺画出15°,75°的角. 用一副三角板还可以拼出哪些度数的角?
135°
120°
15°
75°
新知讲解
如图,借助三角尺画出15°,75°的角. 用一副三角板还可以拼出哪些度数的角?
105°
150°
180°
新知讲解
如图,借助三角尺拼出15°,75°的角. 用一副三角板还可以拼出哪些度数的角?
45°
30°
60°
一共可以拼出的角度有15° 、30°、 45°、 60° 、75° 105° 、120°、 135° 、150° 、180° .
实际上凡是15°的整数倍的角,都可以用三角尺画出.
新知讲解
我们知道,线段的中点把线段分成相等的两条线段.类似地,如图,如果∠AOB=∠BOC,那么射线OB把∠AOC分成两个相等的角.
o
A
C
B
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .
∠BOC
∠AOC
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
射线OB叫做∠AOC的角平分线
新知讲解
α
α
α
A
B
C
D
O
类似地,还有角的三等分线等……
OB、OC是∠AOD的三等分线.
新知讲解
例1 如图O是直线AB上一点,∠AOC=53 17′,求∠BOC的度数.
分析:AB是直线,∠AOB是平角, ∠BOC 和∠AOC的和等于∠AOB.
解:由题意可知, ∠AOB是平角, ∠AOB =∠BOC+∠AOC.
∴ ∠BOC =∠AOB -∠AOC
=180 - 53 17′
=126 43′
o
A
C
B
新知讲解
例2.把一个周角分为7等分,每一份是多少度?(精确到分)
解: 360o÷7
=51o+3o÷7
=51o+180’ ÷7
≈ 51o26’
答:每一份是51°26’的角.
新知讲解
例3计算:
(1);
(2). .
(3).
=17°38'41''
=46°76'94''-29°38'53''
(1)解:47°17'34''-29°38'53''
(2).
=70°45'-17°57'10''
=52°47'50''
新知讲解
(3)
=(33°+24°)+(16'+46')+(28''+37'')
=57°+1°2'+1'5''
=58°3'5''.
用度、分、秒分别相减,注意度、分、秒之间的进制都是60进制,小单位不够减,需要向上一级单位借1.
度、分、秒之间的进制都是60进制,小单位满60需要向上一级单位进1.
新知讲解
例4 如图所示,OE是∠AOB的平分线,OD是∠BOC的平分线,∠AOB=100°,∠EOD=80°,求∠BOC的度数.
解:∵OE是∠AOB的平分线,∠AOB=100°,
∴∠BOE= ∠AOB=50°.
∵∠BOE+∠BOD=∠EOD=80°,
∴∠BOD=∠EOD﹣∠BOE=80°﹣50°=30°.
∵OD是∠BOC的平分线,
∴∠BOC=2∠BOD=60°.
答:∠BOC的度数60°.
课堂练习
1.在同一平面内,已知 , , 则等于( ).
A. 80° B. 40°
C. 80°或40° D. 20°
2.只利用一副学生用的三角尺可以画出的角度为( ).
A. 50° B. 105° C. 35° D. 125°
C
B
课堂练习
3.如图所示,若∠AOB=∠COD , 那么( )
∠1>∠2 B. ∠1=∠2
C. ∠1<∠2 D. 无法比较
4. 已知:∠ 1= ,∠ 2 ,∠ 3= ,则下列说法正确的是( )
∠1=∠2 B. ∠2=∠3
C. ∠1=∠3 D. ∠1、∠2、∠3互不相等
B
C
课堂练习
5. 计算:
(1) .
(2) .
(3) .
(4) .
解:(1)
(2)
=110°90′
=111°30′
课堂练习
(3)
(4)
课堂练习
6. 如图, , , , 平分 ,求 的度数.
解:∵∠AOB=37°,∠BOC=45°,∠COD=40°,
∴∠AOD=122°,
∵OE平分∠AOD,
∴∠AOE= ×122°=61°,
∴∠BOE=∠AOE-∠AOB=61°-37°=24°
A
B
C
D
O
E
课堂练习
∴∠BOM=35°+110°=145°.
7. 如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=70°,求∠BOM的值.
解:∵∠BOD=70°,
∴∠AOC=70°,∠COB=110°,
∵射线OM是∠AOC的平分线,
∴∠COM=35°,
A
B
C
D
O
M
课堂总结
一.角的大小比较
1.度量法:
2.叠合法:
二.角的和差关系
三.角的平分线
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
作业布置
习题4.3
第139页第6题
第140页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
