4.3.3 余角和补角 课件(共35张PPT)
文档属性
| 名称 | 4.3.3 余角和补角 课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 06:52:07 | ||
图片预览










文档简介
(共35张PPT)
人教版七上第四章几何图形初步
4.3.3余角和补角
人教版七年级上册
教学目标
1.一个角的余角与补角,掌握余角和补角的性质.
2.进一步提高学生的抽象概括能力,发展空间观念和知识运用能力.
教学重点:
认识角的互余、互补关系及其性质,确定方位角.
教学难点:
利用余角、补角的概念及性质解决相关问题.
3. 在解决实际问题中,学会用数学的眼光观察现实问题,用数学的思维思考现实问题,用数学语言表达现实问题.
新知导入
观察图中比萨斜塔∠1和∠2有什么数量关系?
2
1
新知讲解
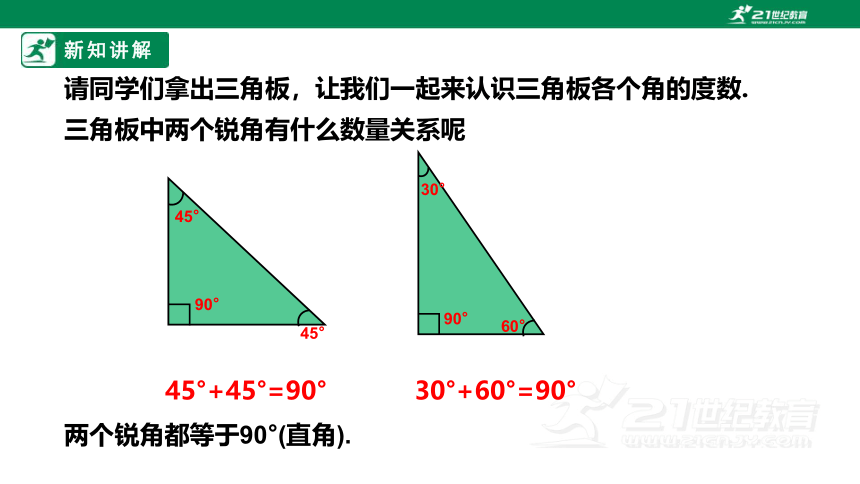
请同学们拿出三角板,让我们一起来认识三角板各个角的度数.
45°
∟
∟
90°
90°
45°
30°
60°
三角板中两个锐角有什么数量关系呢
45°+45°=90°
30°+60°=90°
两个锐角都等于90°(直角).
新知讲解
2
1
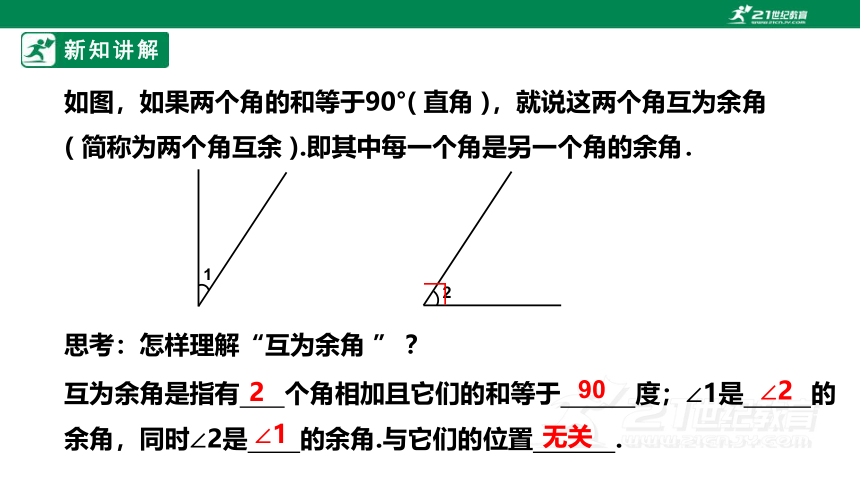
如图,如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).即其中每一个角是另一个角的余角.
∟
思考:怎样理解“互为余角 ” ?
互为余角是指有 个角相加且它们的和等于 度;∠1是 的余角,同时∠2是 的余角.与它们的位置 .
2
∠1
∠2
90
无关
新知讲解
2
1
如图,如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).即其中每一个角是另一个角的余角.
∟
几何语言表示为:
∵∠1+∠2=90°
∴∠1和∠2互为余角
反之 ∵∠1与∠2互为余角
∴∠1+∠2=90°
或 ∴∠1= 90°- ∠2 , ∠2= 90°- ∠1
练一练
1.图中给出的各角,哪些互为余角?
30o
70o
20o
60o
57o
33o
练一练
2.如图∠1=40°,求:①∠1的余角是多少度;
②在∠1上画出它的余角.
1
解:①∠1的余角是:90°-∠1=50°
∟
2
②∠1的余角如图所示:
3
∟
猜想:∠2和∠3有什么数量关系?
新知导入
观察图中比萨斜塔∠1和∠2有什么数量关系?
2
1
∠1+∠2=90°
∠1与∠2互为余角
新知讲解
已知∠1与∠2互为余角, ∠1与∠3互为余角,那么∠2和∠3的有什么数量关系?
解: ∵ ∠1与∠2互余
余角的性质:同角的余角相等.
∴ ∠1+ ∠2 = 90°
∴ ∠2 = 90° -∠1
∵ ∠1与∠3互余
∴ ∠1+ ∠3 = 90°
∴ ∠3 = 90° -∠1
∴ ∠2= ∠3
练一练
∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,求证:∠2=∠4.
解: ∵ ∠1与∠2互余
∴ ∠1+ ∠2 = 90°
∴ ∠2 = 90° -∠1
∵ ∠3与∠4互余
∴ ∠3+ ∠4 = 90°
∴ ∠4 = 90° -∠3
∵ ∠1= ∠3
余角的性质:等角的余角相等.
∴ ∠2= ∠4
归纳
余角的性质:
同(等)角的余角相等.
同角的余角相等
几何语言:
∵ ∠1+ ∠2 = 90°, ∠1+ ∠3 = 90°
∴ ∠2= ∠3
等角的余角相等
几何语言:
∵ ∠1+ ∠2 = 90°, ∠3+ ∠4 = 90°,且∠1= ∠3
∴ ∠2= ∠4
新知讲解
例3 如图,点A,O, B在同一条直线 上,射线OD和射线OE分别平分∠AOC和∠BOC, 图中哪些角互为余角?
O
A
B
C
D
E
同理,∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
所以,∠COD和∠COE互为余角
= (∠AOC+∠BOC)= 90°.
所以∠COD+∠COE= ∠AOC+ ∠BOC
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以 ∠AOC和∠BOC互为补角.
解:因为点A,O, B在同一条直线上,
新知讲解
2
1
如图,如果两个角的和等于180°( 平角 ),就说这两个角互为补角 ( 简称为两个角互补).即其中每一个角是另一个角的补角.
思考:怎样理解“互为补角 ” ?
互为补角是指有 个角相加且它们的和等于 度;∠1是 的补角,同时∠2是 的补角.与它们的位置 .
2
∠1
∠2
180
无关
新知讲解
2
1
如图,如果两个角的和等于180°( 平角 ),就说这两个角互为补角 ( 简称为两个角互补 ).即其中每一个角是另一个角的补角.
几何语言表示为:
∵∠1+∠2=180°
∴∠1和∠2互为补角
反之 ∵∠1与∠2互为补角
∴∠1+∠2=180°
或 ∴∠1= 180°- ∠2 , ∠2= 180°- ∠1
练一练
如图∠1=40°,求:①∠1的补角是多少度;
②在∠1上画出它的补角.
1
解:①∠1的补角是:180°-∠1=140°
2
②∠1的补角如图所示:
3
猜想:∠2和∠3有什么数量关系?
新知讲解
已知∠1与∠2互为补角, ∠1与∠3互为补角,那么∠2和∠3的有什么数量关系?
解: ∵ ∠1与∠2互补
补角的性质:同角的补角相等.
∴ ∠1+ ∠2 = 180°
∴ ∠2 = 180° -∠1
∵ ∠1与∠3互补
∴ ∠1+ ∠3 = 180°
∴ ∠3 = 180° -∠1
∴ ∠2= ∠3
练一练
∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,求证:∠2=∠4.
解: ∵ ∠1与∠2互补
∴ ∠1+ ∠2 = 180°
∴ ∠2 = 180° -∠1
∵ ∠3与∠4互补
∴ ∠3+ ∠4 = 180°
∴ ∠4 = 180° -∠3
∵ ∠1= ∠3
补角的性质:等角的补角相等.
∴ ∠2= ∠4
归纳
补角的性质:
同(等)角的补角相等.
同角的补角相等
几何语言:
∵ ∠1+ ∠2 = 180°, ∠1+ ∠3 = 180°
∴ ∠2= ∠3
等角的补角相等
几何语言:
∵ ∠1+ ∠2 = 180°, ∠3+ ∠4 = 180°,且∠1= ∠3
∴ ∠2= ∠4
新知讲解
∠1 ∠1的余角 ∠1的补角
15
31
40
60
75
(0 < <90 )
观察可得结论:锐角的补角比它的余角大_____.
75°
填表:
165°
59°
149°
50°
140°
30°
150°
15°
105°
75°
165°
90°
新知讲解
例4 若一个角的补角等于它的余角的4倍,求这个角的度数.
解:设这个角是 度,则它的补角是(180°- ),余角是(90°- ),根据题意得:
180°- =4(90°- )
解得: =60°
这个角的度数是60°.
用代数(方程)思想解决几何问题
练一练
已知 ∠A 与∠B 互余,且 ∠A 的度数比∠B 度数的 3 倍还多30°,求∠B的度数.
解:设∠B的度数为 °,则 ∠A 的度数为(3 +30)°. 根据题意得:
故 ∠B 的度数为15°.
解得 =15.
+ ( 3 +30 ) = 90.
新知讲解
八大方位:
射线 OQ
方位角的定义:
以正北、正南的方向为基准,描述运动的方向,如图OA北偏东30°,OB为南偏东25°,这样的表示方向的角叫做方位角.
西北方向:
西南方向:
东北方向:
东南方向:
正东:
正南:
正西:
正北:
30°
25°
O
B
A
C
D
E
F
M
N
P
Q
射线 ON
射线 OP
射线 OM
射线 OE
射线 OD
射线 OC
射线 OF
新知讲解
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上.同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
新知讲解
解:射线OA的方向就是南偏东 60°,即灯塔A所在的方向.
射线 OB的方向就是北偏东40°,即客轮B所在的方向.
射线OC的方向就是南偏西10°,即货轮C所在的方向.
射线OD的方向就是北偏西45°,即海岛D所在的方向.
O
A
B
C
D
60°
40°
10°
45°
课堂练习
1. 若∠A=20° , 则∠A的余角的补角为( )
A. 20° B. 70° C. 110° D. 160°
2. 如图所示,下列说法错误的是( )
A. 射线OA表示东北方向
B. 射线OB表示北偏西30°
C. 射线OC表示南偏西60°
D. 射线OE表示南偏东40°
D
D
课堂练习
3. 已知一个角的余角是20°,则这个角的补角是( )
A. 70° B. 80° C. 110° D. 120°
4. 如图,射线OA表示的方向是( )
东偏南55° B. 南偏东35°
C. 北偏西35° D. 南偏东55°
C
D
课堂练习
5. 如图,∠AOB=∠COD=90°,∠1=23°,求∠2的度数.
解:∵∠AOB=∠COD=90°,
∴∠COB+∠1=∠COB+∠2=90°,
∴∠2=∠1,
∵∠1=23°,
∴∠2=23°
课堂练习
6. 一个角的余角比它的补角的 还少50°,求这个角的度数.
解:设这个角度数为 ,它的余角为 , 补角为 , 根据题意得:
,
解得 ,
∴这个角度数为 .
课堂练习
7. 是∠ 的2倍, 的余角的3倍等于∠ 的补角,求 和∠ 的度数.
解:设∠β为 度,则∠α为2 度,根据题意得,
,
解得: ,
即:∠α=36°,∠β=18°.
课堂练习
8. 如图,直线EF、DG交于点O, OA⊥OB , ∠AOE=35° , ∠GOF=70° ,求 ∠BOD 的度数.
解:因为 OA⊥OB , ∠AOE=35° ,
所以 ∠BOE=90°-35°=55° ,
因为 ∠DOE=∠GOF , ∠GOF=70° ,
所以 ∠DOE=70° ,
所以 ∠BOD=∠DOE-∠BOE=70°-55°=15° .
课堂总结
一.互余和互补的概念:
1.如果两个角的和等于90°(直角),就说这两个角互为余角,简称互余.
2.如果两个角的和等于180 °(平角),就说这两个角互为补角,简称互补.
二.余角和补角的性质:
三.方位角:
方位角是表示方向的角.以正北、正南方向为基准来描述物体所处的方向.
1.同角(或等角)的余角相等.
2.同角(或等角)的补角相等.
作业布置
习题4.3第140页
第12、13题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版七上第四章几何图形初步
4.3.3余角和补角
人教版七年级上册
教学目标
1.一个角的余角与补角,掌握余角和补角的性质.
2.进一步提高学生的抽象概括能力,发展空间观念和知识运用能力.
教学重点:
认识角的互余、互补关系及其性质,确定方位角.
教学难点:
利用余角、补角的概念及性质解决相关问题.
3. 在解决实际问题中,学会用数学的眼光观察现实问题,用数学的思维思考现实问题,用数学语言表达现实问题.
新知导入
观察图中比萨斜塔∠1和∠2有什么数量关系?
2
1
新知讲解
请同学们拿出三角板,让我们一起来认识三角板各个角的度数.
45°
∟
∟
90°
90°
45°
30°
60°
三角板中两个锐角有什么数量关系呢
45°+45°=90°
30°+60°=90°
两个锐角都等于90°(直角).
新知讲解
2
1
如图,如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).即其中每一个角是另一个角的余角.
∟
思考:怎样理解“互为余角 ” ?
互为余角是指有 个角相加且它们的和等于 度;∠1是 的余角,同时∠2是 的余角.与它们的位置 .
2
∠1
∠2
90
无关
新知讲解
2
1
如图,如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).即其中每一个角是另一个角的余角.
∟
几何语言表示为:
∵∠1+∠2=90°
∴∠1和∠2互为余角
反之 ∵∠1与∠2互为余角
∴∠1+∠2=90°
或 ∴∠1= 90°- ∠2 , ∠2= 90°- ∠1
练一练
1.图中给出的各角,哪些互为余角?
30o
70o
20o
60o
57o
33o
练一练
2.如图∠1=40°,求:①∠1的余角是多少度;
②在∠1上画出它的余角.
1
解:①∠1的余角是:90°-∠1=50°
∟
2
②∠1的余角如图所示:
3
∟
猜想:∠2和∠3有什么数量关系?
新知导入
观察图中比萨斜塔∠1和∠2有什么数量关系?
2
1
∠1+∠2=90°
∠1与∠2互为余角
新知讲解
已知∠1与∠2互为余角, ∠1与∠3互为余角,那么∠2和∠3的有什么数量关系?
解: ∵ ∠1与∠2互余
余角的性质:同角的余角相等.
∴ ∠1+ ∠2 = 90°
∴ ∠2 = 90° -∠1
∵ ∠1与∠3互余
∴ ∠1+ ∠3 = 90°
∴ ∠3 = 90° -∠1
∴ ∠2= ∠3
练一练
∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,求证:∠2=∠4.
解: ∵ ∠1与∠2互余
∴ ∠1+ ∠2 = 90°
∴ ∠2 = 90° -∠1
∵ ∠3与∠4互余
∴ ∠3+ ∠4 = 90°
∴ ∠4 = 90° -∠3
∵ ∠1= ∠3
余角的性质:等角的余角相等.
∴ ∠2= ∠4
归纳
余角的性质:
同(等)角的余角相等.
同角的余角相等
几何语言:
∵ ∠1+ ∠2 = 90°, ∠1+ ∠3 = 90°
∴ ∠2= ∠3
等角的余角相等
几何语言:
∵ ∠1+ ∠2 = 90°, ∠3+ ∠4 = 90°,且∠1= ∠3
∴ ∠2= ∠4
新知讲解
例3 如图,点A,O, B在同一条直线 上,射线OD和射线OE分别平分∠AOC和∠BOC, 图中哪些角互为余角?
O
A
B
C
D
E
同理,∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
所以,∠COD和∠COE互为余角
= (∠AOC+∠BOC)= 90°.
所以∠COD+∠COE= ∠AOC+ ∠BOC
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以 ∠AOC和∠BOC互为补角.
解:因为点A,O, B在同一条直线上,
新知讲解
2
1
如图,如果两个角的和等于180°( 平角 ),就说这两个角互为补角 ( 简称为两个角互补).即其中每一个角是另一个角的补角.
思考:怎样理解“互为补角 ” ?
互为补角是指有 个角相加且它们的和等于 度;∠1是 的补角,同时∠2是 的补角.与它们的位置 .
2
∠1
∠2
180
无关
新知讲解
2
1
如图,如果两个角的和等于180°( 平角 ),就说这两个角互为补角 ( 简称为两个角互补 ).即其中每一个角是另一个角的补角.
几何语言表示为:
∵∠1+∠2=180°
∴∠1和∠2互为补角
反之 ∵∠1与∠2互为补角
∴∠1+∠2=180°
或 ∴∠1= 180°- ∠2 , ∠2= 180°- ∠1
练一练
如图∠1=40°,求:①∠1的补角是多少度;
②在∠1上画出它的补角.
1
解:①∠1的补角是:180°-∠1=140°
2
②∠1的补角如图所示:
3
猜想:∠2和∠3有什么数量关系?
新知讲解
已知∠1与∠2互为补角, ∠1与∠3互为补角,那么∠2和∠3的有什么数量关系?
解: ∵ ∠1与∠2互补
补角的性质:同角的补角相等.
∴ ∠1+ ∠2 = 180°
∴ ∠2 = 180° -∠1
∵ ∠1与∠3互补
∴ ∠1+ ∠3 = 180°
∴ ∠3 = 180° -∠1
∴ ∠2= ∠3
练一练
∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,求证:∠2=∠4.
解: ∵ ∠1与∠2互补
∴ ∠1+ ∠2 = 180°
∴ ∠2 = 180° -∠1
∵ ∠3与∠4互补
∴ ∠3+ ∠4 = 180°
∴ ∠4 = 180° -∠3
∵ ∠1= ∠3
补角的性质:等角的补角相等.
∴ ∠2= ∠4
归纳
补角的性质:
同(等)角的补角相等.
同角的补角相等
几何语言:
∵ ∠1+ ∠2 = 180°, ∠1+ ∠3 = 180°
∴ ∠2= ∠3
等角的补角相等
几何语言:
∵ ∠1+ ∠2 = 180°, ∠3+ ∠4 = 180°,且∠1= ∠3
∴ ∠2= ∠4
新知讲解
∠1 ∠1的余角 ∠1的补角
15
31
40
60
75
(0 < <90 )
观察可得结论:锐角的补角比它的余角大_____.
75°
填表:
165°
59°
149°
50°
140°
30°
150°
15°
105°
75°
165°
90°
新知讲解
例4 若一个角的补角等于它的余角的4倍,求这个角的度数.
解:设这个角是 度,则它的补角是(180°- ),余角是(90°- ),根据题意得:
180°- =4(90°- )
解得: =60°
这个角的度数是60°.
用代数(方程)思想解决几何问题
练一练
已知 ∠A 与∠B 互余,且 ∠A 的度数比∠B 度数的 3 倍还多30°,求∠B的度数.
解:设∠B的度数为 °,则 ∠A 的度数为(3 +30)°. 根据题意得:
故 ∠B 的度数为15°.
解得 =15.
+ ( 3 +30 ) = 90.
新知讲解
八大方位:
射线 OQ
方位角的定义:
以正北、正南的方向为基准,描述运动的方向,如图OA北偏东30°,OB为南偏东25°,这样的表示方向的角叫做方位角.
西北方向:
西南方向:
东北方向:
东南方向:
正东:
正南:
正西:
正北:
30°
25°
O
B
A
C
D
E
F
M
N
P
Q
射线 ON
射线 OP
射线 OM
射线 OE
射线 OD
射线 OC
射线 OF
新知讲解
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上.同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
新知讲解
解:射线OA的方向就是南偏东 60°,即灯塔A所在的方向.
射线 OB的方向就是北偏东40°,即客轮B所在的方向.
射线OC的方向就是南偏西10°,即货轮C所在的方向.
射线OD的方向就是北偏西45°,即海岛D所在的方向.
O
A
B
C
D
60°
40°
10°
45°
课堂练习
1. 若∠A=20° , 则∠A的余角的补角为( )
A. 20° B. 70° C. 110° D. 160°
2. 如图所示,下列说法错误的是( )
A. 射线OA表示东北方向
B. 射线OB表示北偏西30°
C. 射线OC表示南偏西60°
D. 射线OE表示南偏东40°
D
D
课堂练习
3. 已知一个角的余角是20°,则这个角的补角是( )
A. 70° B. 80° C. 110° D. 120°
4. 如图,射线OA表示的方向是( )
东偏南55° B. 南偏东35°
C. 北偏西35° D. 南偏东55°
C
D
课堂练习
5. 如图,∠AOB=∠COD=90°,∠1=23°,求∠2的度数.
解:∵∠AOB=∠COD=90°,
∴∠COB+∠1=∠COB+∠2=90°,
∴∠2=∠1,
∵∠1=23°,
∴∠2=23°
课堂练习
6. 一个角的余角比它的补角的 还少50°,求这个角的度数.
解:设这个角度数为 ,它的余角为 , 补角为 , 根据题意得:
,
解得 ,
∴这个角度数为 .
课堂练习
7. 是∠ 的2倍, 的余角的3倍等于∠ 的补角,求 和∠ 的度数.
解:设∠β为 度,则∠α为2 度,根据题意得,
,
解得: ,
即:∠α=36°,∠β=18°.
课堂练习
8. 如图,直线EF、DG交于点O, OA⊥OB , ∠AOE=35° , ∠GOF=70° ,求 ∠BOD 的度数.
解:因为 OA⊥OB , ∠AOE=35° ,
所以 ∠BOE=90°-35°=55° ,
因为 ∠DOE=∠GOF , ∠GOF=70° ,
所以 ∠DOE=70° ,
所以 ∠BOD=∠DOE-∠BOE=70°-55°=15° .
课堂总结
一.互余和互补的概念:
1.如果两个角的和等于90°(直角),就说这两个角互为余角,简称互余.
2.如果两个角的和等于180 °(平角),就说这两个角互为补角,简称互补.
二.余角和补角的性质:
三.方位角:
方位角是表示方向的角.以正北、正南方向为基准来描述物体所处的方向.
1.同角(或等角)的余角相等.
2.同角(或等角)的补角相等.
作业布置
习题4.3第140页
第12、13题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
