2022-2023学年人教版七年级数学下册 5.3.2 平行线的性质和判定及其综合运用 课件 (共28张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册 5.3.2 平行线的性质和判定及其综合运用 课件 (共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 962.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-27 09:29:51 | ||
图片预览



文档简介
(共28张PPT)
平行线的性质和判定的综合运用
1.进一步熟悉平行线的判定方法和性质;
2.运用平行线的性质和判定进行简单的推理和计算;(重点、难点)
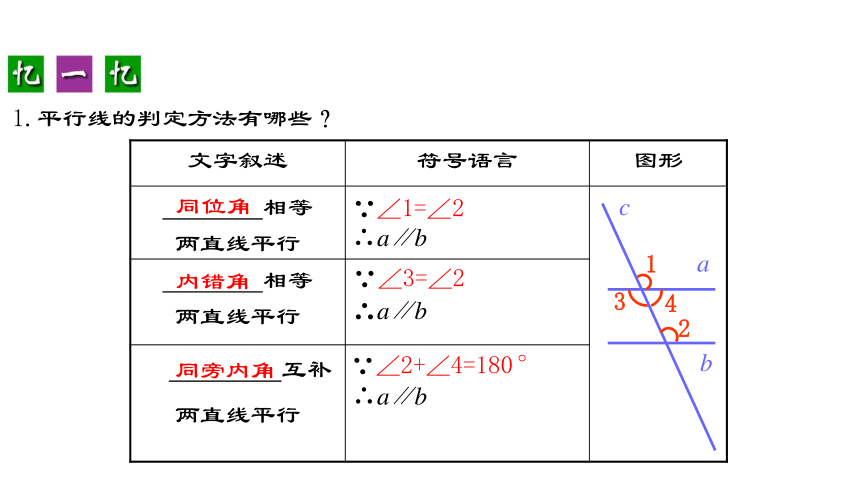
1.平行线的判定方法有哪些?
文字叙述 符号语言 图形
相等 两直线平行 ∴a∥b
相等 两直线平行 ∴a∥b 互补 两直线平行 ∴a∥b 同位角
内错角
同旁内角
∵∠1=∠2
∵∠3=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
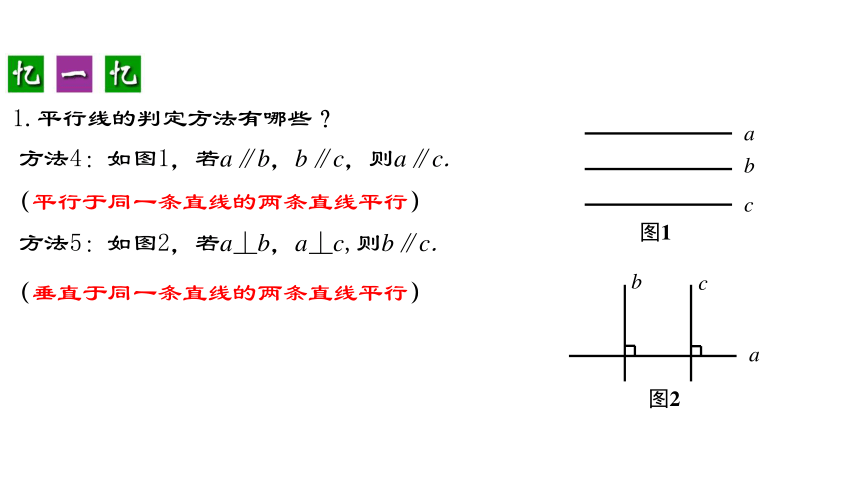
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
a
b
c
图1
a
b
c
图2
1.平行线的判定方法有哪些?
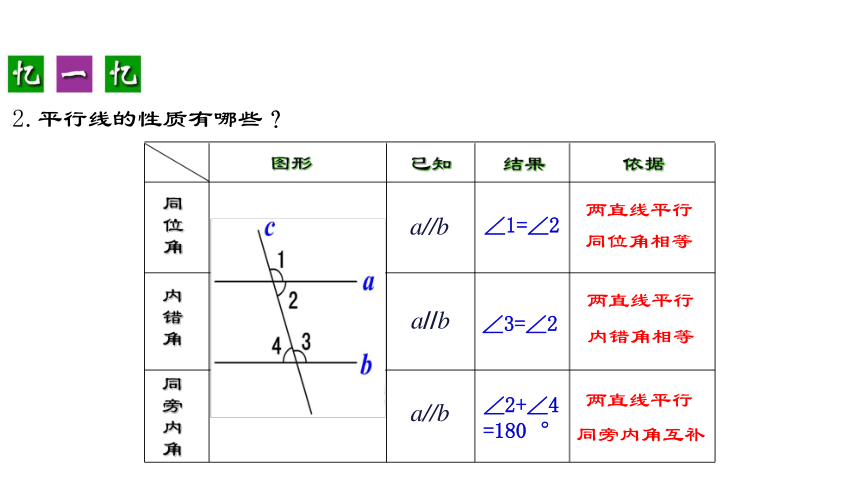
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
2.平行线的性质有哪些?
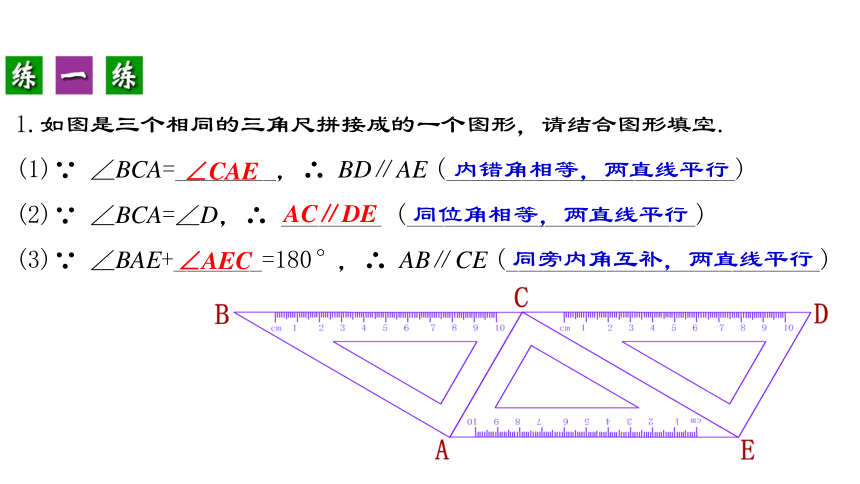
1.如图是三个相同的三角尺拼接成的一个图形,请结合图形填空.
(1)∵ ∠BCA=________,∴ BD∥AE (_______________________)
(2)∵ ∠BCA=∠D,∴ ________ (_______________________)
(3)∵ ∠BAE+_______=180°,∴ AB∥CE (_________________________)
∠CAE
内错角相等,两直线平行
AC∥DE
同位角相等,两直线平行
∠AEC
同旁内角互补,两直线平行
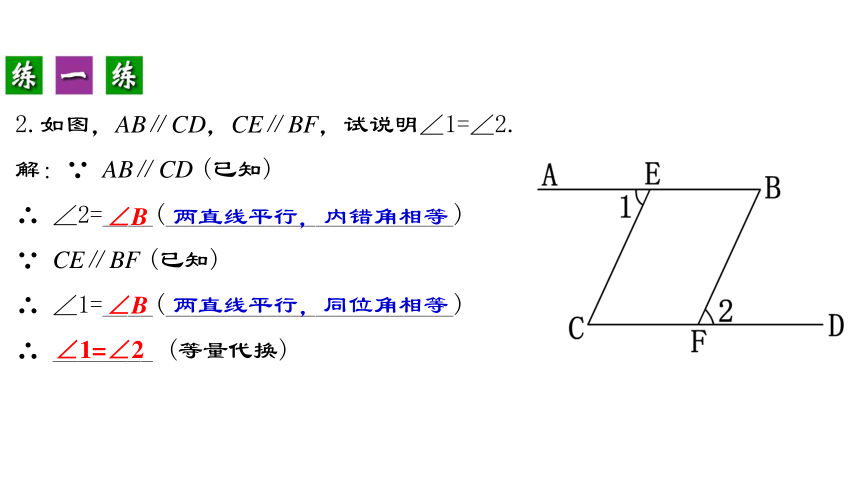
2.如图,AB∥CD,CE∥BF,试说明∠1=∠2.
解:∵ AB∥CD (已知)
∴ ∠2=____(_______________________)
∵ CE∥BF (已知)
∴ ∠1=____(_______________________)
∴ ________ (等量代换)
∠B
两直线平行,内错角相等
∠B
两直线平行,同位角相等
∠1=∠2
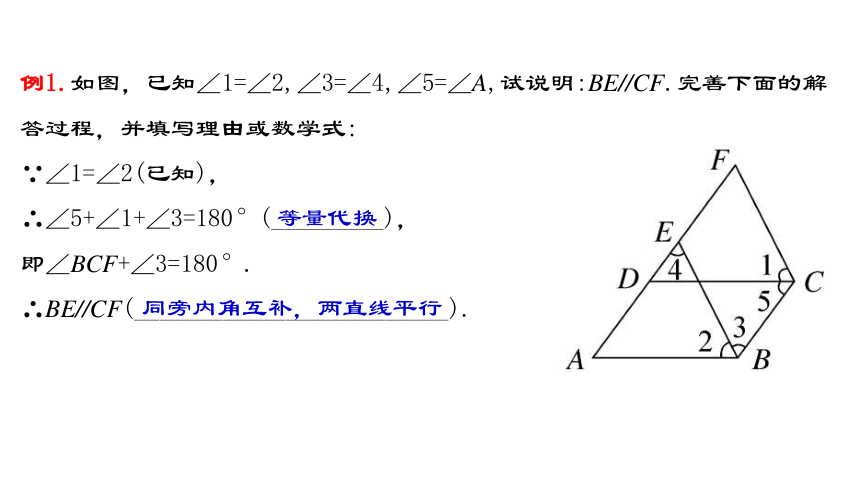
例1.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程,并填写理由或数学式:
解:∵∠3=∠4(已知),
∴AE //_____(________________________).
∴∠EDC=∠5(________________________).
∴∠5=∠A(已知),
∴∠EDC=______(__________).
∴DC//AB(_______________________).
∴∠5+∠ABC=180°(________________________),即∠5+∠2+∠3=180°
BC
内错角相等,两直线平行
两直线平行,内错角相等
∠A
等量代换
同位角相等,两直线平行
同旁内角互补,两直线平行
例1.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程,并填写理由或数学式:
∵∠1=∠2(已知),
∴∠5+∠1+∠3=180°(_________),
即∠BCF+∠3=180°.
∴BE//CF(_________________________).
等量代换
同旁内角互补,两直线平行
如图,AB//CD,AE交CD于点F,点G在AB上,GH⊥BF,垂足为H,∠1=∠2,试说明AE⊥BF.请将下面的解答过程补充完整(填数字式子或理由).
解:∵AB//CD(已知),
∴∠1=______(________________________).
∵∠1=∠2(已知),
∴_____=______(_________).
∴______//_____(_______________________).
又∵GH⊥BF,即∠GHB=90°,
∴∠AFB=∠GHB=90°(______________________).
∴_____ ⊥ _____.
两直线平行,内错角相等
∠A
∠2 ∠A
等量代换
GH AE
同位角相等,两直线平行
两直线平行,同位角相等
AE BF
例2.如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A=∠F,为什么
解:∠AGB=∠DGF (对顶角相等)
∠AGB=∠EHF (已知)
∴∠DGF=∠EHF (等量代换)
∵BD//CE (同位角相等,两直线平行)
∴∠C=∠ABD (两直线平行,同位角相等)
∵∠C=∠D (已知)
∴∠D=∠ABD (等量代换)
∴AC//DF (内错角相等,两直线平行)
∴∠A=∠F (两直线平行,内错角相等)
如图,在三角形ABC中,CD是高,点E, F,G分别在BC,AB,AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
解:DG//BC.理由如下:
∵CD是三角形ABC的高,且EF⊥AB (已知)
∴∠BFE=∠BDC=90° (垂直定义)
∴EF//CD (同位角相等,两直线平行)
∴∠1=∠BCD (两直线平行,同位角相等)
∵∠1=∠2 (已知)
∴∠BCD=∠2 (等量代换)
∴DG//BC (内错角相等,两直线平行)
例3.如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF =∠DEB.
即∠B+∠D=∠DEB.
F
辅助线:为帮助解题而添加的线.辅助线一般画成虚线.
如图,AB//CD,探索∠A、∠C与∠AEC的大小关系 .
解:过点E作EF//AB
∴∠A+∠AEF=180°
∵AB//CD
∴EF//CD
∴∠C+∠CEF=180°
∴∠A+∠C+∠AEC
=∠A+∠C+∠AEF+∠CEF
=360°
即∠A+∠C+∠AEC=360°
F
例4.如图,AB∥CD,试说明∠B、∠D 、∠BED之间的大小关系.
解:∠D+∠BED=∠B
理由:过点E作EF∥AB
∵AB∥CD, EF∥AB (已知)
∴AB∥CD∥EF(平面内两条直线都与同一条
直线平行,这两条直线互相平行)
∴∠B=∠BEF,∠D=∠DEF(两直线平行,内错角相等)
∵∠DEF+∠BED =∠BEF
∴∠D+∠BED=∠B
F
如图,AB∥CD,试说明∠B、∠D 、∠BED之间的大小关系.
解:∠B+∠BED=∠D.
理由:过点E作EF∥AB
∵AB∥CD, EF∥AB (已知)
∴AB∥CD∥EF(平面内两条直线都与同一条
直线平行,这两条直线互相平行)
∴∠B=∠BEF,∠D=∠DEF(两直线平行,内错角相等)
∵∠BEF+∠BED =∠DEF
∴ ∠B+∠BED=∠D
F
∠B+∠D=∠BED
∠B+∠D+∠BED=360°
∠D+∠BED=∠B
∠B+∠BED=∠D
1.如图(1),已知∠1=∠2, ∠3=80°, 则∠4等于( )
A. 80° B.70° C.60° D.50°
2.如图(2),直线a,b,c,d,已知c⊥a, c⊥b,直线b,c,d交于一点,若∠1=50°则∠2等于( )
A.45° B.50° C.60° D.75°
A
B
3.如图,AB//CD,则α, β, γ之间的等量关系为( )
A. α +β+ γ =360° B. α -β+ γ =180°
C. α +β- γ =180° D. α +β+ γ =180°
C
4.如图,AB//EF ,CD⊥EF,∠BAC=50°,则∠ACD=( )
A.120° B.130° C.140° D.150°
5.如图,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上.若∠1=35°,则∠2的度数为( )
A.10° B.25° C.30° D.35°
C
D
6.如图(1)所示,直线a//b,直线c与直线a,b分别相交于点A,B,AM⊥b,垂足为点M,若∠1=58°,则∠2=______.
7.如图(2)所示,若∠1=40°,∠2=40°,∠3=116°40′,则∠4=_______.
8.如图(3)所示,EF//ON,OE平分∠M0N,∠FEO=28°,则∠MFE=____.
32°
63°20′
56°
9.如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
解:(1)DE∥BC.
∵ ∠ADE=60°,∠B=60°
∴ ∠ADE=∠B
∴ DE∥BC (同位角相等,两直线平行)
(2)由(1)得DE∥BC
∴ ∠AED=∠C (两直线平行,同位角相等)
又∵ ∠AED=40°
∴ ∠C=40°
10.如图,在△ABC中,点D、E分别在BC、AB上,且EF//AD,∠1+∠2=180°.
(1)试猜想∠2与∠BAD的关系,并说明理由;
解:(1)∠2=∠BAD.
理由:∵EF//AD
∴∠1+∠BAD=180°
∵∠1+∠2= 180°
∴∠2=∠BAD
10.如图,在△ABC中,点D、E分别在BC、AB上,且EF//AD,∠1+∠2=180°.
(2)若DG平分∠ADC,试说明:DG // AB.
(2)∵DG平分∠ADC
∴∠2=∠ADG
由(1)知∠2=∠BAD,
∴∠ADG=∠BAD
∴DG//AB
11.如图,AB//CD,点C在BE上,AE交CD于点F,∠1=∠2,∠3=∠4,
试说明:AD//BE.
解:∵AB //CD
∴∠BAF=∠4
∵∠3=∠4
∴∠3=∠BAF
∵∠1=∠2
∴∠BAF=∠CAD
∴∠3=∠CAD
∴AD//BE
12.已知直线AB//CD,点M,N分别在直线AB,CD上,点P是平面内一个动点,且满足∠MPN=90°,过点N作射线NQ,使得∠PNQ=∠PNC.
(1)如图①,当射线NQ与NM重合,∠QND=50°时,则∠AMP=______;
25°
F
(2)如图②,当射线NQ与NM不重合,∠QND=α时,求∠AMP的度数(用含α的式子表示);
解:如图②,过P作PF//AB
∵AB//CD
∴AB//PF//CD
∴∠AMP=∠MPF , ∠CNP=∠FPN
∴∠MPN=∠AMP+∠PNC
∵∠MPN=90°
∴∠AMP+∠PNC=90°
∵∠PNQ=∠PNC,∠QND=α
∴∠PNC==90°-α.
∴∠AMP=90°-90°+α=α
(3)请直接写出在点P运动的过程中,∠QND与∠AMP之间的数量关系
____________________.
∠AMP=∠QND
平行线的性质和判定的综合运用
1.进一步熟悉平行线的判定方法和性质;
2.运用平行线的性质和判定进行简单的推理和计算;(重点、难点)
1.平行线的判定方法有哪些?
文字叙述 符号语言 图形
相等 两直线平行 ∴a∥b
相等 两直线平行 ∴a∥b 互补 两直线平行 ∴a∥b 同位角
内错角
同旁内角
∵∠1=∠2
∵∠3=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
a
b
c
图1
a
b
c
图2
1.平行线的判定方法有哪些?
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
2.平行线的性质有哪些?
1.如图是三个相同的三角尺拼接成的一个图形,请结合图形填空.
(1)∵ ∠BCA=________,∴ BD∥AE (_______________________)
(2)∵ ∠BCA=∠D,∴ ________ (_______________________)
(3)∵ ∠BAE+_______=180°,∴ AB∥CE (_________________________)
∠CAE
内错角相等,两直线平行
AC∥DE
同位角相等,两直线平行
∠AEC
同旁内角互补,两直线平行
2.如图,AB∥CD,CE∥BF,试说明∠1=∠2.
解:∵ AB∥CD (已知)
∴ ∠2=____(_______________________)
∵ CE∥BF (已知)
∴ ∠1=____(_______________________)
∴ ________ (等量代换)
∠B
两直线平行,内错角相等
∠B
两直线平行,同位角相等
∠1=∠2
例1.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程,并填写理由或数学式:
解:∵∠3=∠4(已知),
∴AE //_____(________________________).
∴∠EDC=∠5(________________________).
∴∠5=∠A(已知),
∴∠EDC=______(__________).
∴DC//AB(_______________________).
∴∠5+∠ABC=180°(________________________),即∠5+∠2+∠3=180°
BC
内错角相等,两直线平行
两直线平行,内错角相等
∠A
等量代换
同位角相等,两直线平行
同旁内角互补,两直线平行
例1.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程,并填写理由或数学式:
∵∠1=∠2(已知),
∴∠5+∠1+∠3=180°(_________),
即∠BCF+∠3=180°.
∴BE//CF(_________________________).
等量代换
同旁内角互补,两直线平行
如图,AB//CD,AE交CD于点F,点G在AB上,GH⊥BF,垂足为H,∠1=∠2,试说明AE⊥BF.请将下面的解答过程补充完整(填数字式子或理由).
解:∵AB//CD(已知),
∴∠1=______(________________________).
∵∠1=∠2(已知),
∴_____=______(_________).
∴______//_____(_______________________).
又∵GH⊥BF,即∠GHB=90°,
∴∠AFB=∠GHB=90°(______________________).
∴_____ ⊥ _____.
两直线平行,内错角相等
∠A
∠2 ∠A
等量代换
GH AE
同位角相等,两直线平行
两直线平行,同位角相等
AE BF
例2.如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A=∠F,为什么
解:∠AGB=∠DGF (对顶角相等)
∠AGB=∠EHF (已知)
∴∠DGF=∠EHF (等量代换)
∵BD//CE (同位角相等,两直线平行)
∴∠C=∠ABD (两直线平行,同位角相等)
∵∠C=∠D (已知)
∴∠D=∠ABD (等量代换)
∴AC//DF (内错角相等,两直线平行)
∴∠A=∠F (两直线平行,内错角相等)
如图,在三角形ABC中,CD是高,点E, F,G分别在BC,AB,AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
解:DG//BC.理由如下:
∵CD是三角形ABC的高,且EF⊥AB (已知)
∴∠BFE=∠BDC=90° (垂直定义)
∴EF//CD (同位角相等,两直线平行)
∴∠1=∠BCD (两直线平行,同位角相等)
∵∠1=∠2 (已知)
∴∠BCD=∠2 (等量代换)
∴DG//BC (内错角相等,两直线平行)
例3.如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF =∠DEB.
即∠B+∠D=∠DEB.
F
辅助线:为帮助解题而添加的线.辅助线一般画成虚线.
如图,AB//CD,探索∠A、∠C与∠AEC的大小关系 .
解:过点E作EF//AB
∴∠A+∠AEF=180°
∵AB//CD
∴EF//CD
∴∠C+∠CEF=180°
∴∠A+∠C+∠AEC
=∠A+∠C+∠AEF+∠CEF
=360°
即∠A+∠C+∠AEC=360°
F
例4.如图,AB∥CD,试说明∠B、∠D 、∠BED之间的大小关系.
解:∠D+∠BED=∠B
理由:过点E作EF∥AB
∵AB∥CD, EF∥AB (已知)
∴AB∥CD∥EF(平面内两条直线都与同一条
直线平行,这两条直线互相平行)
∴∠B=∠BEF,∠D=∠DEF(两直线平行,内错角相等)
∵∠DEF+∠BED =∠BEF
∴∠D+∠BED=∠B
F
如图,AB∥CD,试说明∠B、∠D 、∠BED之间的大小关系.
解:∠B+∠BED=∠D.
理由:过点E作EF∥AB
∵AB∥CD, EF∥AB (已知)
∴AB∥CD∥EF(平面内两条直线都与同一条
直线平行,这两条直线互相平行)
∴∠B=∠BEF,∠D=∠DEF(两直线平行,内错角相等)
∵∠BEF+∠BED =∠DEF
∴ ∠B+∠BED=∠D
F
∠B+∠D=∠BED
∠B+∠D+∠BED=360°
∠D+∠BED=∠B
∠B+∠BED=∠D
1.如图(1),已知∠1=∠2, ∠3=80°, 则∠4等于( )
A. 80° B.70° C.60° D.50°
2.如图(2),直线a,b,c,d,已知c⊥a, c⊥b,直线b,c,d交于一点,若∠1=50°则∠2等于( )
A.45° B.50° C.60° D.75°
A
B
3.如图,AB//CD,则α, β, γ之间的等量关系为( )
A. α +β+ γ =360° B. α -β+ γ =180°
C. α +β- γ =180° D. α +β+ γ =180°
C
4.如图,AB//EF ,CD⊥EF,∠BAC=50°,则∠ACD=( )
A.120° B.130° C.140° D.150°
5.如图,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上.若∠1=35°,则∠2的度数为( )
A.10° B.25° C.30° D.35°
C
D
6.如图(1)所示,直线a//b,直线c与直线a,b分别相交于点A,B,AM⊥b,垂足为点M,若∠1=58°,则∠2=______.
7.如图(2)所示,若∠1=40°,∠2=40°,∠3=116°40′,则∠4=_______.
8.如图(3)所示,EF//ON,OE平分∠M0N,∠FEO=28°,则∠MFE=____.
32°
63°20′
56°
9.如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
解:(1)DE∥BC.
∵ ∠ADE=60°,∠B=60°
∴ ∠ADE=∠B
∴ DE∥BC (同位角相等,两直线平行)
(2)由(1)得DE∥BC
∴ ∠AED=∠C (两直线平行,同位角相等)
又∵ ∠AED=40°
∴ ∠C=40°
10.如图,在△ABC中,点D、E分别在BC、AB上,且EF//AD,∠1+∠2=180°.
(1)试猜想∠2与∠BAD的关系,并说明理由;
解:(1)∠2=∠BAD.
理由:∵EF//AD
∴∠1+∠BAD=180°
∵∠1+∠2= 180°
∴∠2=∠BAD
10.如图,在△ABC中,点D、E分别在BC、AB上,且EF//AD,∠1+∠2=180°.
(2)若DG平分∠ADC,试说明:DG // AB.
(2)∵DG平分∠ADC
∴∠2=∠ADG
由(1)知∠2=∠BAD,
∴∠ADG=∠BAD
∴DG//AB
11.如图,AB//CD,点C在BE上,AE交CD于点F,∠1=∠2,∠3=∠4,
试说明:AD//BE.
解:∵AB //CD
∴∠BAF=∠4
∵∠3=∠4
∴∠3=∠BAF
∵∠1=∠2
∴∠BAF=∠CAD
∴∠3=∠CAD
∴AD//BE
12.已知直线AB//CD,点M,N分别在直线AB,CD上,点P是平面内一个动点,且满足∠MPN=90°,过点N作射线NQ,使得∠PNQ=∠PNC.
(1)如图①,当射线NQ与NM重合,∠QND=50°时,则∠AMP=______;
25°
F
(2)如图②,当射线NQ与NM不重合,∠QND=α时,求∠AMP的度数(用含α的式子表示);
解:如图②,过P作PF//AB
∵AB//CD
∴AB//PF//CD
∴∠AMP=∠MPF , ∠CNP=∠FPN
∴∠MPN=∠AMP+∠PNC
∵∠MPN=90°
∴∠AMP+∠PNC=90°
∵∠PNQ=∠PNC,∠QND=α
∴∠PNC==90°-α.
∴∠AMP=90°-90°+α=α
(3)请直接写出在点P运动的过程中,∠QND与∠AMP之间的数量关系
____________________.
∠AMP=∠QND
