2022-2023学年人教版七年级数学上册第4章 几何图形初步 整理与复习 课件(共68张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学上册第4章 几何图形初步 整理与复习 课件(共68张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 696.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-27 09:34:41 | ||
图片预览





文档简介
(共68张PPT)
整理与复习
第四章 几何图形初步
1. 了解常见的平面图形与立体图形.
2. 理解“直线、射线、线段”等相关概念.
3. 理解并掌握角的大小的比较方法,互为余角、互为补角的概念及其性质.
一、几何图形
二、直线、射线、线段
三、角
知识点梳理
一、几何图形
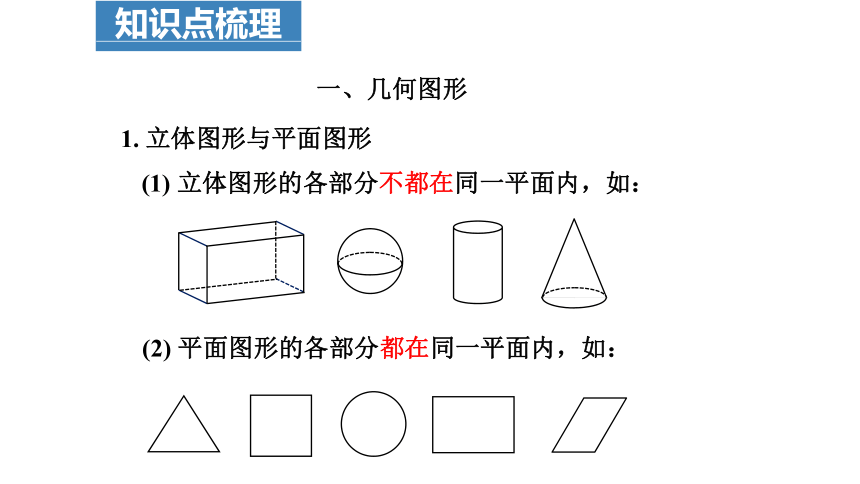
1. 立体图形与平面图形
(1) 立体图形的各部分不都在同一平面内,如:
(2) 平面图形的各部分都在同一平面内,如:
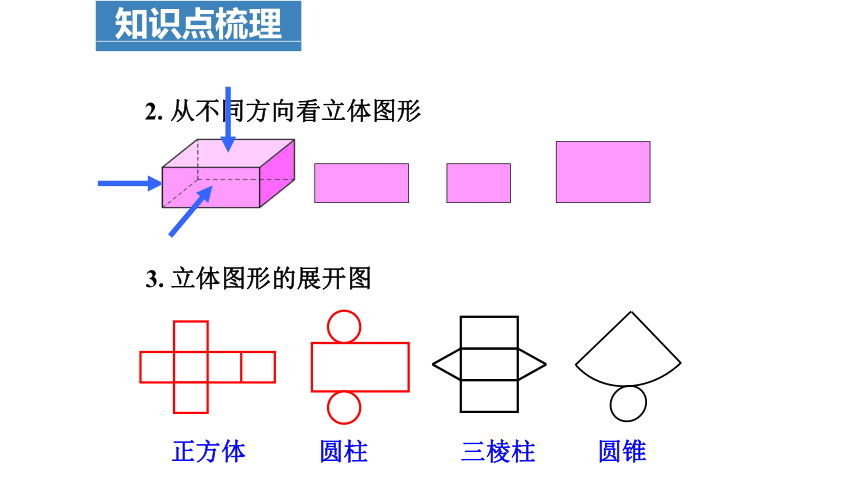
2. 从不同方向看立体图形
3. 立体图形的展开图
正方体
圆柱
三棱柱
圆锥
知识点梳理
4. 点、线、面、体之间的联系
(1) 体是由面围成,面与面相交成线,线与线相交成点;
(2) 点动成线、线动成面、面动成体.
知识点梳理
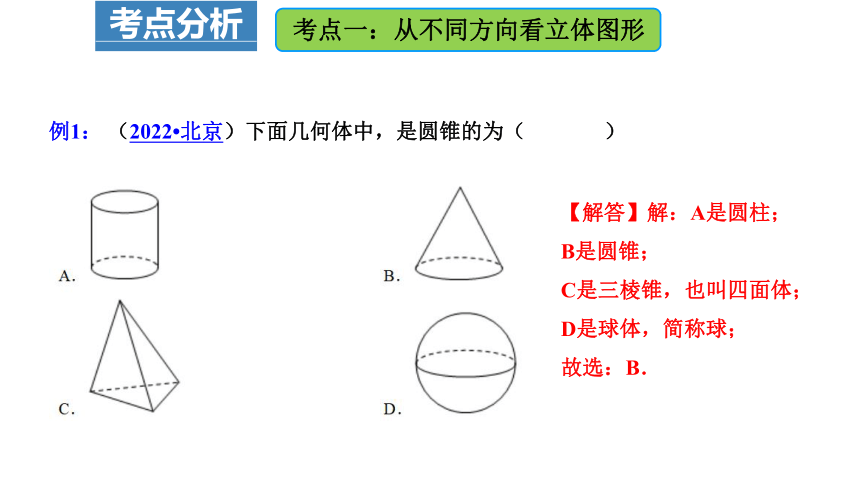
例1: (2022 北京)下面几何体中,是圆锥的为( )
【解答】解:A是圆柱;
B是圆锥;
C是三棱锥,也叫四面体;
D是球体,简称球;
故选:B.
考点一:从不同方向看立体图形
考点分析
例2: (4分)(2020 重庆B卷2/26)围成下列立体图形的各个面中,每个面都是平的是( )
A. 长方体 B. 圆柱体
C. 球体 D. 圆锥体
【解答】解:A、六个面都是平面,故本选项正确;
B、侧面不是平面,故本选项错误;
C、球面不是平面,故本选项错误;
D、侧面不是平面,故本选项错误;
故选:A.
【点评】本题考查的是立体图形的认识,掌握平面与曲面的概念是解题的关键.
考点分析
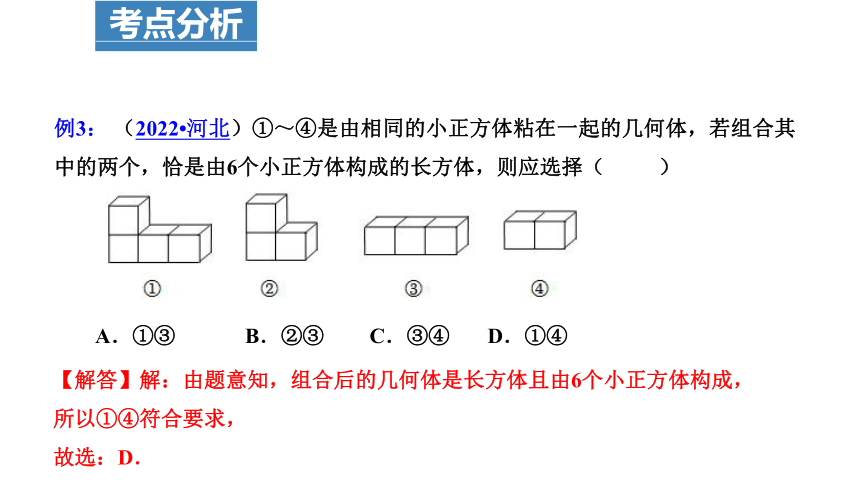
例3: (2022 河北)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
【解答】解:由题意知,组合后的几何体是长方体且由6个小正方体构成,
所以①④符合要求,
故选:D.
考点分析
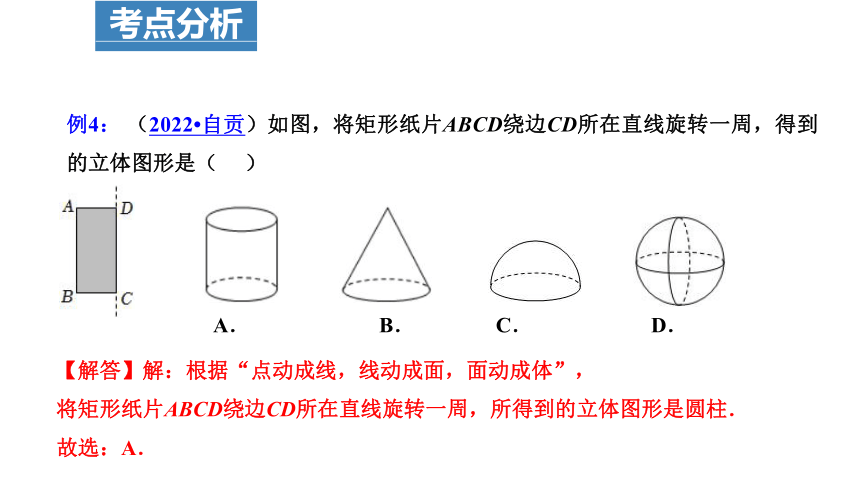
例4: (2022 自贡)如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
【解答】解:根据“点动成线,线动成面,面动成体”,
将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.
故选:A.
A. B. C. D.
考点分析
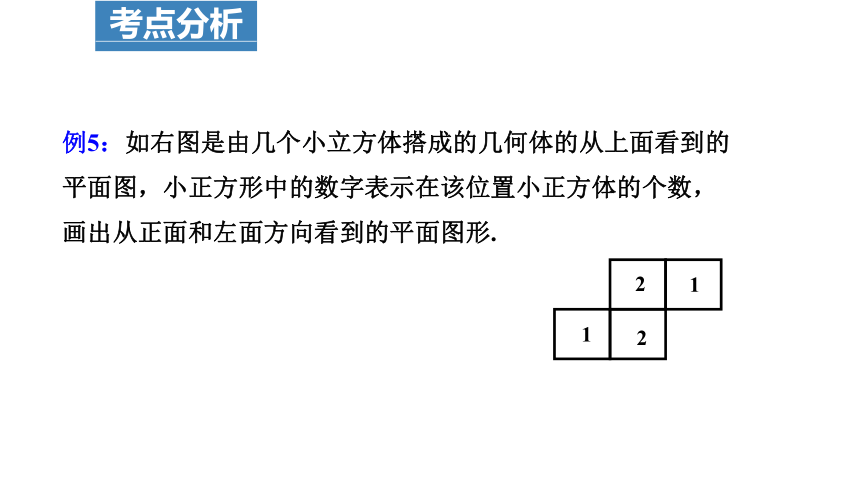
例5:如右图是由几个小立方体搭成的几何体的从上面看到的平面图,小正方形中的数字表示在该位置小正方体的个数,画出从正面和左面方向看到的平面图形.
1
1
2
2
考点分析
1
1
2
2
从正面看
从左面看
解:
解析:根据图中的数字,可知从前面看有3列,从左到右的个数分别是1,2,1;从左面看有2列,个数都是2 .
考点分析
如图,从正面看A,B,C,D四个立体图形,分别得到 a,b,c,d 四个平面图形,把上下两行相对应立体图形与平面图形用线连接起来.
A B C D
a b c d
针对训练
例6: (2022 柳州)如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
【解答】解:将矩形绕着它的一边所在的直线l旋转一周,可以得到圆柱体,
故选:B.
考点二:立体图形的展开图
考点分析
例7:根据下列多面体的平面展开图,填写多面体的名称
(1)_______,(2)_______,(3)________.
长方体
三棱柱
三棱锥
(1) (2) (3)
考点分析
1. 在下列图形中 (每个小四边形皆为相同的正方形),可以是一个正方体展开图的是 ( )
A B C D
C
2. 把长、宽分别为4cm、9cm的长方形纸片围成一个圆柱,则圆柱的底面半径为 .
13 cm
针对训练
二、直线、射线、线段
1. 有关直线的基本事实
经过两点有一条直线,并且只有一条直线.
2. 直线、射线、线段的区别
类型
线段
射线
直线
端点个数
2个
不能延伸
延伸性
能否度量
可度量
1个
向一个方向
无限延伸
不可度量
无端点
向两个方向
无限延伸
不可度量
知识点梳理
3. 基本作图
(1) 作一线段等于已知线段;
(2) 利用尺规作图作一条线段等于两条线段的和、差.
5. 有关线段的基本事实:
两点之间,线段最短.
4. 线段的中点
应用格式:
C是线段AB的中点,
AC =BC = AB,
AB =2AC =2BC.
A
C
B
6. 连接两点的线段的长度,叫做这两点间的距离.
知识点梳理
例8: (2022 桂林)如图,点C是线段AB的中点,若AC=2 cm,则AB= cm.
【解答】解:根据中点的定义可得:AB=2AC=2×2=4 cm,
故答案为:4.
【点评】本题主要考查中点的定义,熟知中点的定义是解题关键.
考点三:线段长度的计算
考点分析
例9: (3分)(2021 包头3/26)已知线段AB=4,在直线AB上作线段BC,使得BC=2,若D是线段AC的中点,则线段AD的长为( )
A.1 B.3 C.1或3 D.2或3
【分析】根据题意可分为两种情况,①点C在线段AB上,可计算出AC的长,再由D是线段AC的中点,即可得出答案;②BC在线段AB的延长线上,可计算出AC的长,再由D是线段AC的中点,即可得出答案.
考点分析
【解答】解:根据题意分两种情况,
①如图1:
∵AB=4,BC=2,
∴AC=AB-BC=2,
∵D是线段AC的中点,
∴ ;
考点分析
②如图2:
∵AB=4,BC=2,
∴AC=AB+BC=6,
∵D是线段AC的中点,
∴ .
∴线段AD的长为1或3.
故选:C.
考点分析
例10:如图,已知点 C 为 AB 上一点,AC =15 cm,
CB= AC,D,E 分别为 AC,AB 的中点,求DE 的长.
E
C
A
D
B
解:∵AC =15cm,CB = AC,
∴CB = ×15=9 cm,∴AB =15+9= 24 cm.
∵D,E 分别为 AC,AB 的中点,
∴AE = AB =12 cm,DC = AC = 7.5 cm,
∴DE = AE-AD =12-7.5 = 4.5 (cm).
考点分析
例11:如图,B,C 两点把线段 AD 分成 2:5:3 三部分,M 为 AD 的中点,MC = 6 cm,求线段 BM 和 AD 的长.
D
A
B
C
M
提示:题目中线段间有明显的倍分关系,且和差关系较为复杂,可以尝试列方程解答.
考点分析
由 MC + CD= MD得,3x + 6 = 5x. 解得 x = 3.
故 BM = AM- AB =5x-2x = 3x = 3×3 = 9 (cm),
AD =10x =10×3 = 30 (cm).
D
A
B
C
M
解:设 AB = 2x cm,
BC = 5x cm,CD = 3x cm,
则 AD = AB+BC+CD =10x cm.
∵M 是 AD 的中点,
∴AM = MD = AD = 5x cm.
考点分析
例12:点 C 在线段 AB所在的直线上,点M,N分别是 AC,BC的中点.
(1) 如图,AC = 8 cm,CB = 6 cm,求线段MN的长;
A M C N B
∴CM= AC=4 (cm),CN= BC=3 (cm),
解:∵点M,N分别是AC,BC的中点,
∴MN=CM+CN=4+3=7 (cm).
考点分析
(2) 若 C 为线段 AB 上任一点,满足 AC + CB = a cm,其它条件不变,你能猜想 MN 的长度吗?并说明理由;
A M C N B
证明:同(1)可得
CM = AC ,CN = BC,
∴ MN = CM+CN = AC+ BC
= (AC+BC) = a (cm).
猜想:MN = a cm.
考点分析
(3) 若C 在线段 AB的延长线上,且满足 AC-BC = b cm,M,N分别为AC,BC的中点,你能猜想 MN 的长度吗?请画出图形,并说明理由.
A M B N C
MN = MC-NC
= AC- BC
= (AC-BC) = b (cm).
猜想:MN= b cm.
证明:根据题意画出图形,由图可得
考点分析
1. 如图:线段 AB = 100 cm,点 C,D 在线段 AB 上. 点 M 是线段 AD 的中点,MD = 21 cm,BC = 34 cm . 则线段 MC 的长度为__________.
B
A
M
C
D
2. 如图:AB =120 cm,点C,D在线段AB上,BD = 3BC,点 D 是线段 AC 的中点. 则线段 BD 的长度为______.
B
A
C
D
45cm
72cm
针对训练
3. 已知:点 A,B,C 在一直线上,AB =12 cm,BC = 4 cm. 点 M,N 分别是线段 AB,BC 的中点. 求线段 MN 的长度.
A M C N B
图①
∴ BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm),
解:如图①,当 C 在 AB 间时,
∵ M,N 分别是 AB,BC 的中点,
∴ MN = BM-BN = 6-2 = 4 (cm).
针对训练
方法总结:无图条件下,注意多解情况要分类讨论,培养分类意识.
C
A
M
N
B
图②
∴ BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm)
如图②,当C在线段AB外时,
∵ M,N 分别是 AB,BC 的中点,
∴ MN = BM + BN = 6 + 2 = 8 (cm).
针对训练
例13: (2022 柳州)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.① B.② C.③ D.④
【解答】解:根据题意可得,
从学校A到书店B有①、②、③、④四条路线,其中最短的路线是②.
故选:B.
考点四:关于线段的基本事实
考点分析
例14:如图,是一个三级台阶,A 和 B是这个台阶的两个相对的端点,A 点上有一只蚂蚁,想到 B 点去吃可口的食物. 若这只蚂蚁从 A 点出发,沿着台阶面爬到B 点,你能画出蚂蚁爬行的最短路线吗?
A
B
考点分析
解:如图,将台阶面展开成平面图形. 连接 AB 两点,因为两点之间线段最短,所以线段AB 为蚂蚁爬行的最短路线.
A
B
考点分析
B
B
如图,在A点有一只壁虎,要沿着圆柱体的表面爬到B点去吃蚊子. 请画出壁虎在圆柱体表面爬行的最短路线.
A
针对训练
三、角
1. 角的定义
(1) 有公共端点的两条射线组成的图形,叫做角;
(2) 角也可以看作由一条射线绕着它的端点旋转而形成的图形.
2. 角的度量
度、分、秒的互化:
1°=60′,1′=60″
知识点梳理
3. 角的平分线
O
B
A
C
应用格式:
OC 是 ∠AOB 的角平分线,
∠AOC =∠BOC = ∠AOB
∠AOB = 2∠BOC = 2∠AOC
知识点梳理
4. 余角和补角
(1) 定义:① 如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
② 如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
(2) 性质:① 同角 (等角) 的补角相等.
② 同角 (等角) 的余角相等.
知识点梳理
(3) 方位角
① 定义:物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向.
② 书写:通常要先写北或南,再写偏东或偏西
知识点梳理
例15: (3分)(2021 呼伦贝尔 兴安盟14/26) °.
【解答】解: ,
,
,
,
故答案为:74.325.
【点评】本题考查度、分、秒的换算,掌握度、分、秒的换算进率和换算方法是得出正确答案的前提.
考点五:角的度量及角度的计算
考点分析
例16: 如图所示,用量角器度量∠AOB,可以读出∠AOB的度数为( ).
A. 45° B. 55° C. 125° D. 135°
B
考点分析
例17: (2022 百色)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为 °.
【解答】解:根据题意可得,
∠BAC=90°+45°=135°.
故答案为:135.
考点分析
例18: (2022 湘潭)如图,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF= .
考点分析
【解答】解:因为一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,
所以∠EDO=∠CDB=20°,∠AEF=∠OED,
在△ODE中,∠OED=180°-∠AOB-∠EDO=180°-120°-20°=40°,
所以∠AEF=∠OED=40°.
故答案为:40°.
考点分析
例19:如图,BD平分∠ABC,BE 把∠ABC 分成 2︰5 两部分,∠DBE=21°,求∠ABC的度数.
E
B
A
C
D
∴ ∠ABD= ∠ABC =3.5x°.
解:设∠ABE = 2x°,则∠CBE = 5x°,
∠ABC =∠ABE+∠CBE= 7x°.
∵ BD 平分∠ABC,
∵∠ABE+∠DBE =∠ABD ,即2x + 21= 3.5x.
解得 x = 14.
∴ ∠ABC = 7x°= 7×14°= 98 °.
考点分析
例20:如图,∠AOB是直角, ON是∠AOC的平分线,OM是∠BOC的平分线.
(1) 当∠AOC=50°时,求∠MON的大小;
O
B
M
A
N
C
提示:先求出∠BOC的度数,再根据角平分线的定义求出∠COM,∠CON,然后根据∠MON=∠COM-∠CON代入数据进行计算即可得解.
考点分析
∴∠MON=∠COM-∠CON=70°-25°=45°.
O
B
M
A
N
C
解:∵∠AOB是直角,∠AOC=50°,
∴∠BOC =∠AOB+∠AOC
= 90°+50°=140°,
∵ON是∠AOC的平分线,
OM是∠BOC的平分线,
∴∠COM = ∠BOC = ×140°=70°,
∠CON= ∠AOC = ×50°= 25°,
考点分析
(2) 当∠AOC=α 时, ∠MON等于多少度?
O
B
M
A
N
C
∴∠MON=∠COM-∠CON= (90°+α)-α=45°.
解:∠BOC=∠AOB+∠AOC
=90°+α,
∵ON是∠AOC的平分线,
OM是∠BOC的平分线,
∠CON= ∠AOC = α,
∴∠COM= ∠BOC = (90°+α),
考点分析
(3) 当锐角∠AOC的大小发生改变时,∠MON的大小也会发生改变吗?为什么?
解:不会发生变化.
由(2)可知∠MON的大小与∠AOC无关,总是等于∠AOB的一半.
O
B
M
A
N
C
考点分析
2. 若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°, 则 ( )
A. ∠A>∠B>∠C B. ∠B>∠A>∠C
C. ∠A>∠C>∠B D. ∠C>∠A>∠B
A
3. 19点整时,时钟上时针与分针之间的夹角是 ( )
A. 210° B. 30° C. 150° D. 60°
C
1. 以∠AOB的顶点O为射线端点,在∠AOB的内部画出3条射线,在所成的图形中角的总个数是( )
A. 4 B. 6 C. 8 D. 10
D
针对训练
5. 已知AC是∠AOB的平分线,∠AOB=68°,则∠AOC= .
34°
4. 三叶吊扇绕轴至少旋转 度,才能与起始位置重合.
6. 把一个直角纸片的直角对折后再对折,每次对折时使角的两边重合,那么所形成的角的度数是 .
22 .5°
120
针对训练
7. 已知一条射线 OA,若从点 O 再引两条射线 OB 和OC,使∠AOB=50°,∠BOC=10°,求∠AOC的度数.
解:有两种情况:
(1)如图①所示:
∠AOC =∠AOB+∠BOC
=50°+10°=60°;
O
A
C
B
图①
针对训练
(2)如图②所示:
∠AOC =∠AOB-∠BOC
=50°-10°=40°.
综上所述,∠AOC的度数为60°或40°.
O
A
C
B
图②
针对训练
例21: (2022 甘肃)若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
【解答】解:因为∠A=40°,
所以∠A的余角为:90°-40°=50°,
故选:A.
【点评】本题考查的是余角的定义,如果两个角的和等于90°,就说这两个角互为余角.
考点六:余角和补角
考点分析
例22: (2022 连云港)已知∠A的补角为60°,则∠A = °.
【解答】解:因为∠A的补角为60°,
所以∠A =180°-60°=120°,
故答案为:120.
【点评】本题考查了余角和补角,掌握如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角是解题的关键.
考点分析
例23: (3分)(2020 通辽4/26)如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A. B.
C. D.
考点分析
【分析】根据余角和补角的概念、结合图形进行判断即可.
【解答】解:A.∠α与∠β互余,故本选项正确;
B.∠α =∠β,故本选项错误;
C.∠α =∠β,故本选项错误;
D.∠α与∠β互补,故本选项错误,
故选:A.
【点评】本题考查了余角和补角,是基础题,熟记概念与性质是解题的关键.
考点分析
例24:已知∠α和∠β互为补角,并且∠β的一半比∠α小30 ,求∠α,∠β.
解:设∠α=x ,则∠β=180 -x .
根据题意 ∠β=2(∠α-30 ),
得 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80 ,∠β=100 .
提示:此题和差倍分关系较复杂,可列方程解答.
考点分析
例25:如图,直线AB,CD相交于点O,OF平分∠AOE,∠FOD=90°.
(1) 写出图中所有与∠AOD互补的角;
解:∵直线AB,CD相交于点O,
∴∠AOC和∠BOD与∠AOD 互补,
∵OF平分∠AOE,∴∠AOF=∠EOF,
∵∠FOD=90°,
∴∠COF=180°-∠FOD=90°.
又∵∠AOC=∠COF-∠AOF=90°-∠EOF,
∠DOE=∠FOD-∠EOF=90°-∠EOF,
∴∠AOC=∠DOE.
∴与∠AOD互补的角有∠AOC,∠BOD,∠DOE.
O
A
C
B
D
E
F
考点分析
(2) 若∠AOE=120°,求∠BOD的度数.
O
A
C
B
D
E
F
∴∠AOF = ∠AOE= ×120°=60°.
解:∵OF平分∠AOE,
由(1)知,∠COF=90°,
∴∠AOC=∠COF-∠AOF=90°-60°=30°.
由(1)知,∠AOC和∠BOD与∠AOD 互补,
∴∠BOD=∠AOC=30°(同角的补角相等).
考点分析
例26:已知∠AOB=90°,∠COD=90°,画出示意图并探究∠AOC与∠BOD的关系.
解:如图①,∵∠AOB = 90°,
∠COD = 90°,
∴∠AOC = 90°-∠BOC,
∠BOD = 90°-∠BOC,
∴∠AOC =∠BOD;
如图②,∠AOC=90°+∠BOC,
∠BOD=90°-∠BOC,
∴∠AOC+∠BOD=180°;
D
O
A
C
B
图①
D
O
A
C
B
图②
考点分析
如图③,∵∠AOB=90°,∠COD=90°,
∴∠AOC=90°+∠BOC,
∠BOD=90°+∠BOC,
∴∠AOC=∠BOD;
如图④,∠AOC+∠BOD=360°-90°×2=180°,
∴∠AOC+∠BOD=180°.
综上所述,∠AOC =∠BOD 或∠AOC+∠BOD=180°.
O
A
C
B
D
图③
O
A
C
B
D
图④
考点分析
1. 如果一个角的余角与它的补角互补,则这个角为( )
A. 30° B. 60° C. 45° D. 90°
2. 如果∠1与∠2互补,∠2为锐角,则下列表示∠2余角的式子是( )
A. 90°-∠1 B. ∠1-90°
C. ∠1+90° D. 90°-∠1
B
C
3. 一个角为35°39′,则这个角的余角为 ,补角为 .
144°21′
54°21′
针对训练
4. 如图,直线AB,CD相交于点O,OA平分∠EOC.
(1) 若∠EOC=70°,求∠BOD的度数;
O
A
C
B
D
E
∴∠AOC = ∠EOC
= ×70°=35°.
解:∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=180°-∠AOD.
∵OA平分∠EOC,
∴∠BOD =∠AOC =35°.
针对训练
(2) 若∠EOC : ∠EOD=2:3,求∠BOD的度数.
解:设∠EOC=2x°∠EOD=3x°,
由∠EOC+∠EOD=180°得
2x+3x =180°,
解得x = 36°.
∴∠EOC = 2x°=72°,
∴∠AOC= ∠EOC= ×72°=36°,
∠BOD=∠AOC=36°.
O
A
C
B
D
E
针对训练
例27:一只蚂蚁从 O 点出发,沿东北方向爬行 2.5 cm,碰到障碍物 B 后,折向北偏西60°方向爬行3 cm到 C点.
(1) 画出蚂蚁的爬行路线;
(2) 求出∠OBC的度数.
北
O
B
2.5 cm
C
3 cm
60°
45°
解:(1) 如图所示;
(2) ∠OBC =75°.
考点七:方位角
考点分析
A看B的方向为北偏西50°,那么B看A的方向是 .
南偏东50°
针对训练
课堂小结
几何图形
立体图形
平面图形
展开或从不同方向看
面动成体
平面图形
直线、射线、线段
角
表示方法
线段长短的比较与运算
两个基本事实
中点
表示方法
角的度量、比较与运算
余角和补角
角平分线
概念、性质
整理与复习
第四章 几何图形初步
1. 了解常见的平面图形与立体图形.
2. 理解“直线、射线、线段”等相关概念.
3. 理解并掌握角的大小的比较方法,互为余角、互为补角的概念及其性质.
一、几何图形
二、直线、射线、线段
三、角
知识点梳理
一、几何图形
1. 立体图形与平面图形
(1) 立体图形的各部分不都在同一平面内,如:
(2) 平面图形的各部分都在同一平面内,如:
2. 从不同方向看立体图形
3. 立体图形的展开图
正方体
圆柱
三棱柱
圆锥
知识点梳理
4. 点、线、面、体之间的联系
(1) 体是由面围成,面与面相交成线,线与线相交成点;
(2) 点动成线、线动成面、面动成体.
知识点梳理
例1: (2022 北京)下面几何体中,是圆锥的为( )
【解答】解:A是圆柱;
B是圆锥;
C是三棱锥,也叫四面体;
D是球体,简称球;
故选:B.
考点一:从不同方向看立体图形
考点分析
例2: (4分)(2020 重庆B卷2/26)围成下列立体图形的各个面中,每个面都是平的是( )
A. 长方体 B. 圆柱体
C. 球体 D. 圆锥体
【解答】解:A、六个面都是平面,故本选项正确;
B、侧面不是平面,故本选项错误;
C、球面不是平面,故本选项错误;
D、侧面不是平面,故本选项错误;
故选:A.
【点评】本题考查的是立体图形的认识,掌握平面与曲面的概念是解题的关键.
考点分析
例3: (2022 河北)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
【解答】解:由题意知,组合后的几何体是长方体且由6个小正方体构成,
所以①④符合要求,
故选:D.
考点分析
例4: (2022 自贡)如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
【解答】解:根据“点动成线,线动成面,面动成体”,
将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.
故选:A.
A. B. C. D.
考点分析
例5:如右图是由几个小立方体搭成的几何体的从上面看到的平面图,小正方形中的数字表示在该位置小正方体的个数,画出从正面和左面方向看到的平面图形.
1
1
2
2
考点分析
1
1
2
2
从正面看
从左面看
解:
解析:根据图中的数字,可知从前面看有3列,从左到右的个数分别是1,2,1;从左面看有2列,个数都是2 .
考点分析
如图,从正面看A,B,C,D四个立体图形,分别得到 a,b,c,d 四个平面图形,把上下两行相对应立体图形与平面图形用线连接起来.
A B C D
a b c d
针对训练
例6: (2022 柳州)如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
【解答】解:将矩形绕着它的一边所在的直线l旋转一周,可以得到圆柱体,
故选:B.
考点二:立体图形的展开图
考点分析
例7:根据下列多面体的平面展开图,填写多面体的名称
(1)_______,(2)_______,(3)________.
长方体
三棱柱
三棱锥
(1) (2) (3)
考点分析
1. 在下列图形中 (每个小四边形皆为相同的正方形),可以是一个正方体展开图的是 ( )
A B C D
C
2. 把长、宽分别为4cm、9cm的长方形纸片围成一个圆柱,则圆柱的底面半径为 .
13 cm
针对训练
二、直线、射线、线段
1. 有关直线的基本事实
经过两点有一条直线,并且只有一条直线.
2. 直线、射线、线段的区别
类型
线段
射线
直线
端点个数
2个
不能延伸
延伸性
能否度量
可度量
1个
向一个方向
无限延伸
不可度量
无端点
向两个方向
无限延伸
不可度量
知识点梳理
3. 基本作图
(1) 作一线段等于已知线段;
(2) 利用尺规作图作一条线段等于两条线段的和、差.
5. 有关线段的基本事实:
两点之间,线段最短.
4. 线段的中点
应用格式:
C是线段AB的中点,
AC =BC = AB,
AB =2AC =2BC.
A
C
B
6. 连接两点的线段的长度,叫做这两点间的距离.
知识点梳理
例8: (2022 桂林)如图,点C是线段AB的中点,若AC=2 cm,则AB= cm.
【解答】解:根据中点的定义可得:AB=2AC=2×2=4 cm,
故答案为:4.
【点评】本题主要考查中点的定义,熟知中点的定义是解题关键.
考点三:线段长度的计算
考点分析
例9: (3分)(2021 包头3/26)已知线段AB=4,在直线AB上作线段BC,使得BC=2,若D是线段AC的中点,则线段AD的长为( )
A.1 B.3 C.1或3 D.2或3
【分析】根据题意可分为两种情况,①点C在线段AB上,可计算出AC的长,再由D是线段AC的中点,即可得出答案;②BC在线段AB的延长线上,可计算出AC的长,再由D是线段AC的中点,即可得出答案.
考点分析
【解答】解:根据题意分两种情况,
①如图1:
∵AB=4,BC=2,
∴AC=AB-BC=2,
∵D是线段AC的中点,
∴ ;
考点分析
②如图2:
∵AB=4,BC=2,
∴AC=AB+BC=6,
∵D是线段AC的中点,
∴ .
∴线段AD的长为1或3.
故选:C.
考点分析
例10:如图,已知点 C 为 AB 上一点,AC =15 cm,
CB= AC,D,E 分别为 AC,AB 的中点,求DE 的长.
E
C
A
D
B
解:∵AC =15cm,CB = AC,
∴CB = ×15=9 cm,∴AB =15+9= 24 cm.
∵D,E 分别为 AC,AB 的中点,
∴AE = AB =12 cm,DC = AC = 7.5 cm,
∴DE = AE-AD =12-7.5 = 4.5 (cm).
考点分析
例11:如图,B,C 两点把线段 AD 分成 2:5:3 三部分,M 为 AD 的中点,MC = 6 cm,求线段 BM 和 AD 的长.
D
A
B
C
M
提示:题目中线段间有明显的倍分关系,且和差关系较为复杂,可以尝试列方程解答.
考点分析
由 MC + CD= MD得,3x + 6 = 5x. 解得 x = 3.
故 BM = AM- AB =5x-2x = 3x = 3×3 = 9 (cm),
AD =10x =10×3 = 30 (cm).
D
A
B
C
M
解:设 AB = 2x cm,
BC = 5x cm,CD = 3x cm,
则 AD = AB+BC+CD =10x cm.
∵M 是 AD 的中点,
∴AM = MD = AD = 5x cm.
考点分析
例12:点 C 在线段 AB所在的直线上,点M,N分别是 AC,BC的中点.
(1) 如图,AC = 8 cm,CB = 6 cm,求线段MN的长;
A M C N B
∴CM= AC=4 (cm),CN= BC=3 (cm),
解:∵点M,N分别是AC,BC的中点,
∴MN=CM+CN=4+3=7 (cm).
考点分析
(2) 若 C 为线段 AB 上任一点,满足 AC + CB = a cm,其它条件不变,你能猜想 MN 的长度吗?并说明理由;
A M C N B
证明:同(1)可得
CM = AC ,CN = BC,
∴ MN = CM+CN = AC+ BC
= (AC+BC) = a (cm).
猜想:MN = a cm.
考点分析
(3) 若C 在线段 AB的延长线上,且满足 AC-BC = b cm,M,N分别为AC,BC的中点,你能猜想 MN 的长度吗?请画出图形,并说明理由.
A M B N C
MN = MC-NC
= AC- BC
= (AC-BC) = b (cm).
猜想:MN= b cm.
证明:根据题意画出图形,由图可得
考点分析
1. 如图:线段 AB = 100 cm,点 C,D 在线段 AB 上. 点 M 是线段 AD 的中点,MD = 21 cm,BC = 34 cm . 则线段 MC 的长度为__________.
B
A
M
C
D
2. 如图:AB =120 cm,点C,D在线段AB上,BD = 3BC,点 D 是线段 AC 的中点. 则线段 BD 的长度为______.
B
A
C
D
45cm
72cm
针对训练
3. 已知:点 A,B,C 在一直线上,AB =12 cm,BC = 4 cm. 点 M,N 分别是线段 AB,BC 的中点. 求线段 MN 的长度.
A M C N B
图①
∴ BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm),
解:如图①,当 C 在 AB 间时,
∵ M,N 分别是 AB,BC 的中点,
∴ MN = BM-BN = 6-2 = 4 (cm).
针对训练
方法总结:无图条件下,注意多解情况要分类讨论,培养分类意识.
C
A
M
N
B
图②
∴ BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm)
如图②,当C在线段AB外时,
∵ M,N 分别是 AB,BC 的中点,
∴ MN = BM + BN = 6 + 2 = 8 (cm).
针对训练
例13: (2022 柳州)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.① B.② C.③ D.④
【解答】解:根据题意可得,
从学校A到书店B有①、②、③、④四条路线,其中最短的路线是②.
故选:B.
考点四:关于线段的基本事实
考点分析
例14:如图,是一个三级台阶,A 和 B是这个台阶的两个相对的端点,A 点上有一只蚂蚁,想到 B 点去吃可口的食物. 若这只蚂蚁从 A 点出发,沿着台阶面爬到B 点,你能画出蚂蚁爬行的最短路线吗?
A
B
考点分析
解:如图,将台阶面展开成平面图形. 连接 AB 两点,因为两点之间线段最短,所以线段AB 为蚂蚁爬行的最短路线.
A
B
考点分析
B
B
如图,在A点有一只壁虎,要沿着圆柱体的表面爬到B点去吃蚊子. 请画出壁虎在圆柱体表面爬行的最短路线.
A
针对训练
三、角
1. 角的定义
(1) 有公共端点的两条射线组成的图形,叫做角;
(2) 角也可以看作由一条射线绕着它的端点旋转而形成的图形.
2. 角的度量
度、分、秒的互化:
1°=60′,1′=60″
知识点梳理
3. 角的平分线
O
B
A
C
应用格式:
OC 是 ∠AOB 的角平分线,
∠AOC =∠BOC = ∠AOB
∠AOB = 2∠BOC = 2∠AOC
知识点梳理
4. 余角和补角
(1) 定义:① 如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
② 如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
(2) 性质:① 同角 (等角) 的补角相等.
② 同角 (等角) 的余角相等.
知识点梳理
(3) 方位角
① 定义:物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向.
② 书写:通常要先写北或南,再写偏东或偏西
知识点梳理
例15: (3分)(2021 呼伦贝尔 兴安盟14/26) °.
【解答】解: ,
,
,
,
故答案为:74.325.
【点评】本题考查度、分、秒的换算,掌握度、分、秒的换算进率和换算方法是得出正确答案的前提.
考点五:角的度量及角度的计算
考点分析
例16: 如图所示,用量角器度量∠AOB,可以读出∠AOB的度数为( ).
A. 45° B. 55° C. 125° D. 135°
B
考点分析
例17: (2022 百色)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为 °.
【解答】解:根据题意可得,
∠BAC=90°+45°=135°.
故答案为:135.
考点分析
例18: (2022 湘潭)如图,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF= .
考点分析
【解答】解:因为一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,
所以∠EDO=∠CDB=20°,∠AEF=∠OED,
在△ODE中,∠OED=180°-∠AOB-∠EDO=180°-120°-20°=40°,
所以∠AEF=∠OED=40°.
故答案为:40°.
考点分析
例19:如图,BD平分∠ABC,BE 把∠ABC 分成 2︰5 两部分,∠DBE=21°,求∠ABC的度数.
E
B
A
C
D
∴ ∠ABD= ∠ABC =3.5x°.
解:设∠ABE = 2x°,则∠CBE = 5x°,
∠ABC =∠ABE+∠CBE= 7x°.
∵ BD 平分∠ABC,
∵∠ABE+∠DBE =∠ABD ,即2x + 21= 3.5x.
解得 x = 14.
∴ ∠ABC = 7x°= 7×14°= 98 °.
考点分析
例20:如图,∠AOB是直角, ON是∠AOC的平分线,OM是∠BOC的平分线.
(1) 当∠AOC=50°时,求∠MON的大小;
O
B
M
A
N
C
提示:先求出∠BOC的度数,再根据角平分线的定义求出∠COM,∠CON,然后根据∠MON=∠COM-∠CON代入数据进行计算即可得解.
考点分析
∴∠MON=∠COM-∠CON=70°-25°=45°.
O
B
M
A
N
C
解:∵∠AOB是直角,∠AOC=50°,
∴∠BOC =∠AOB+∠AOC
= 90°+50°=140°,
∵ON是∠AOC的平分线,
OM是∠BOC的平分线,
∴∠COM = ∠BOC = ×140°=70°,
∠CON= ∠AOC = ×50°= 25°,
考点分析
(2) 当∠AOC=α 时, ∠MON等于多少度?
O
B
M
A
N
C
∴∠MON=∠COM-∠CON= (90°+α)-α=45°.
解:∠BOC=∠AOB+∠AOC
=90°+α,
∵ON是∠AOC的平分线,
OM是∠BOC的平分线,
∠CON= ∠AOC = α,
∴∠COM= ∠BOC = (90°+α),
考点分析
(3) 当锐角∠AOC的大小发生改变时,∠MON的大小也会发生改变吗?为什么?
解:不会发生变化.
由(2)可知∠MON的大小与∠AOC无关,总是等于∠AOB的一半.
O
B
M
A
N
C
考点分析
2. 若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°, 则 ( )
A. ∠A>∠B>∠C B. ∠B>∠A>∠C
C. ∠A>∠C>∠B D. ∠C>∠A>∠B
A
3. 19点整时,时钟上时针与分针之间的夹角是 ( )
A. 210° B. 30° C. 150° D. 60°
C
1. 以∠AOB的顶点O为射线端点,在∠AOB的内部画出3条射线,在所成的图形中角的总个数是( )
A. 4 B. 6 C. 8 D. 10
D
针对训练
5. 已知AC是∠AOB的平分线,∠AOB=68°,则∠AOC= .
34°
4. 三叶吊扇绕轴至少旋转 度,才能与起始位置重合.
6. 把一个直角纸片的直角对折后再对折,每次对折时使角的两边重合,那么所形成的角的度数是 .
22 .5°
120
针对训练
7. 已知一条射线 OA,若从点 O 再引两条射线 OB 和OC,使∠AOB=50°,∠BOC=10°,求∠AOC的度数.
解:有两种情况:
(1)如图①所示:
∠AOC =∠AOB+∠BOC
=50°+10°=60°;
O
A
C
B
图①
针对训练
(2)如图②所示:
∠AOC =∠AOB-∠BOC
=50°-10°=40°.
综上所述,∠AOC的度数为60°或40°.
O
A
C
B
图②
针对训练
例21: (2022 甘肃)若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
【解答】解:因为∠A=40°,
所以∠A的余角为:90°-40°=50°,
故选:A.
【点评】本题考查的是余角的定义,如果两个角的和等于90°,就说这两个角互为余角.
考点六:余角和补角
考点分析
例22: (2022 连云港)已知∠A的补角为60°,则∠A = °.
【解答】解:因为∠A的补角为60°,
所以∠A =180°-60°=120°,
故答案为:120.
【点评】本题考查了余角和补角,掌握如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角是解题的关键.
考点分析
例23: (3分)(2020 通辽4/26)如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A. B.
C. D.
考点分析
【分析】根据余角和补角的概念、结合图形进行判断即可.
【解答】解:A.∠α与∠β互余,故本选项正确;
B.∠α =∠β,故本选项错误;
C.∠α =∠β,故本选项错误;
D.∠α与∠β互补,故本选项错误,
故选:A.
【点评】本题考查了余角和补角,是基础题,熟记概念与性质是解题的关键.
考点分析
例24:已知∠α和∠β互为补角,并且∠β的一半比∠α小30 ,求∠α,∠β.
解:设∠α=x ,则∠β=180 -x .
根据题意 ∠β=2(∠α-30 ),
得 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80 ,∠β=100 .
提示:此题和差倍分关系较复杂,可列方程解答.
考点分析
例25:如图,直线AB,CD相交于点O,OF平分∠AOE,∠FOD=90°.
(1) 写出图中所有与∠AOD互补的角;
解:∵直线AB,CD相交于点O,
∴∠AOC和∠BOD与∠AOD 互补,
∵OF平分∠AOE,∴∠AOF=∠EOF,
∵∠FOD=90°,
∴∠COF=180°-∠FOD=90°.
又∵∠AOC=∠COF-∠AOF=90°-∠EOF,
∠DOE=∠FOD-∠EOF=90°-∠EOF,
∴∠AOC=∠DOE.
∴与∠AOD互补的角有∠AOC,∠BOD,∠DOE.
O
A
C
B
D
E
F
考点分析
(2) 若∠AOE=120°,求∠BOD的度数.
O
A
C
B
D
E
F
∴∠AOF = ∠AOE= ×120°=60°.
解:∵OF平分∠AOE,
由(1)知,∠COF=90°,
∴∠AOC=∠COF-∠AOF=90°-60°=30°.
由(1)知,∠AOC和∠BOD与∠AOD 互补,
∴∠BOD=∠AOC=30°(同角的补角相等).
考点分析
例26:已知∠AOB=90°,∠COD=90°,画出示意图并探究∠AOC与∠BOD的关系.
解:如图①,∵∠AOB = 90°,
∠COD = 90°,
∴∠AOC = 90°-∠BOC,
∠BOD = 90°-∠BOC,
∴∠AOC =∠BOD;
如图②,∠AOC=90°+∠BOC,
∠BOD=90°-∠BOC,
∴∠AOC+∠BOD=180°;
D
O
A
C
B
图①
D
O
A
C
B
图②
考点分析
如图③,∵∠AOB=90°,∠COD=90°,
∴∠AOC=90°+∠BOC,
∠BOD=90°+∠BOC,
∴∠AOC=∠BOD;
如图④,∠AOC+∠BOD=360°-90°×2=180°,
∴∠AOC+∠BOD=180°.
综上所述,∠AOC =∠BOD 或∠AOC+∠BOD=180°.
O
A
C
B
D
图③
O
A
C
B
D
图④
考点分析
1. 如果一个角的余角与它的补角互补,则这个角为( )
A. 30° B. 60° C. 45° D. 90°
2. 如果∠1与∠2互补,∠2为锐角,则下列表示∠2余角的式子是( )
A. 90°-∠1 B. ∠1-90°
C. ∠1+90° D. 90°-∠1
B
C
3. 一个角为35°39′,则这个角的余角为 ,补角为 .
144°21′
54°21′
针对训练
4. 如图,直线AB,CD相交于点O,OA平分∠EOC.
(1) 若∠EOC=70°,求∠BOD的度数;
O
A
C
B
D
E
∴∠AOC = ∠EOC
= ×70°=35°.
解:∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=180°-∠AOD.
∵OA平分∠EOC,
∴∠BOD =∠AOC =35°.
针对训练
(2) 若∠EOC : ∠EOD=2:3,求∠BOD的度数.
解:设∠EOC=2x°∠EOD=3x°,
由∠EOC+∠EOD=180°得
2x+3x =180°,
解得x = 36°.
∴∠EOC = 2x°=72°,
∴∠AOC= ∠EOC= ×72°=36°,
∠BOD=∠AOC=36°.
O
A
C
B
D
E
针对训练
例27:一只蚂蚁从 O 点出发,沿东北方向爬行 2.5 cm,碰到障碍物 B 后,折向北偏西60°方向爬行3 cm到 C点.
(1) 画出蚂蚁的爬行路线;
(2) 求出∠OBC的度数.
北
O
B
2.5 cm
C
3 cm
60°
45°
解:(1) 如图所示;
(2) ∠OBC =75°.
考点七:方位角
考点分析
A看B的方向为北偏西50°,那么B看A的方向是 .
南偏东50°
针对训练
课堂小结
几何图形
立体图形
平面图形
展开或从不同方向看
面动成体
平面图形
直线、射线、线段
角
表示方法
线段长短的比较与运算
两个基本事实
中点
表示方法
角的度量、比较与运算
余角和补角
角平分线
概念、性质
