2022-2023学年人教版七年级数学下册 第五章 相交线与平行线 章节复习(共48张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册 第五章 相交线与平行线 章节复习(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-27 09:39:12 | ||
图片预览








文档简介
(共48张PPT)
相交线与平行线 章节复习
1.进一步熟悉相交线所成的角及其基本结论;
2.进一步理解垂线、垂线段的概念及性质,点到直线的距离;
3.熟练掌握三线八角(同位角、内错角、同旁内角),两直线平行的判定及其应用;
4.熟练掌握平行线的性质及一些结论,并会应用;
5.平移的特征并会应用其解决问题.
1.邻补角:形如∠1与∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角.
2.对顶角:形如∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
性质:对顶角相等.
一、相交线
性质:邻补角互补.
3.垂直:当两条直线相交所构成的四个角中有一个是直角,我们就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线;互相垂直的两条直线的交点叫做垂足.
如右图,直线AB与直线CD垂直,
记作:AB⊥CD,垂足是O;
直线m与直线n垂直,
记作:m⊥n;
m
n
“⊥”是“垂直”的记号,读作“垂直于”;
而“┐”是图形中“垂直”(直角)的标记.
一、相交线
垂线的性质1:经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线.
即在同一平面内,过一点有且只有一条直线与已知直线垂直.
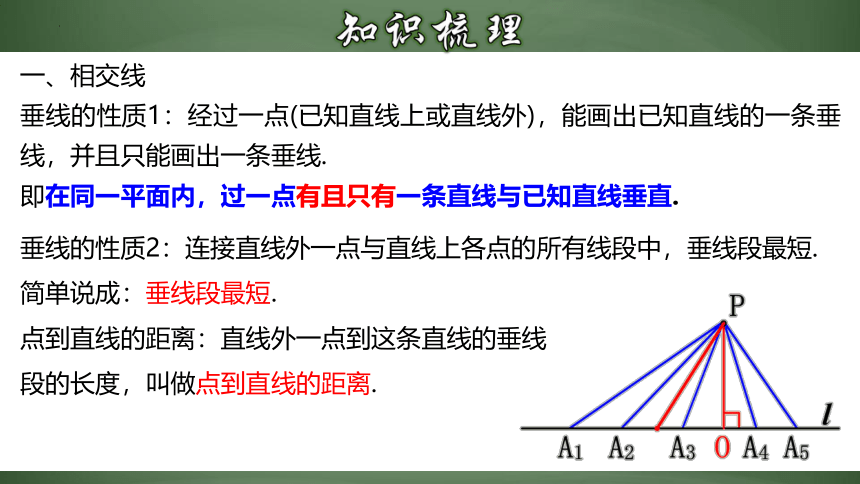
垂线的性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线
段的长度,叫做点到直线的距离.
一、相交线
一、相交线
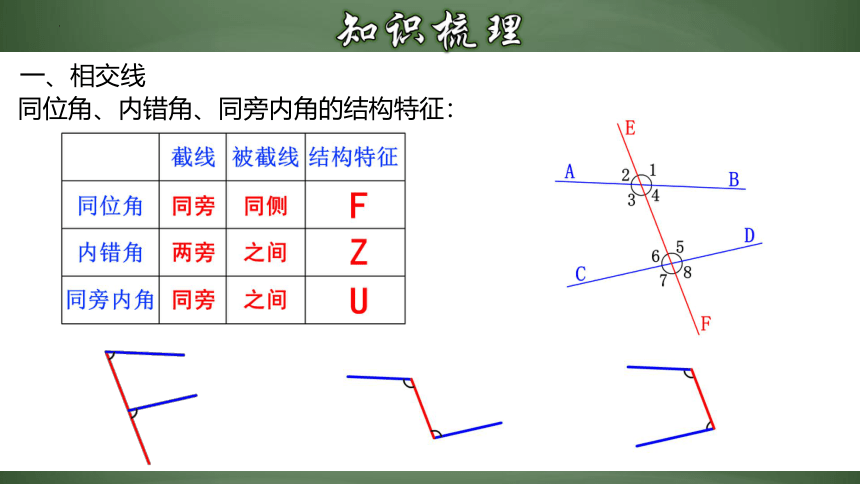
两角的位置分别在直线AB,CD的同一方(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫做同位角.
4.三线八角:
两角的位置都在直线AB,CD之间,并且分别在直线EF两侧(∠3在直线EF左侧,∠5在直线EF右侧),具有这种位置关系的一对角叫做内错角.
两角的位置都在直线AB,CD之间,并且都在直线EF的同一旁(左侧),具有这种位置关系的一对角叫做同旁内角.
同位角、内错角、同旁内角的结构特征:
一、相交线
1.平行线定义:在同一个平面内,不相交的两条直线叫做平行线.
(在同一平面内,不重合的两条直线只有两种位置关系:相交和平行.)
2.表示法:通常用“∥”表示平行,读作“平行于”.
如下图中直线AB与直线CD平行,记作AB∥CD.
如果用l,m表示这两条直线,那么直线l与直线 m平行记作l∥m.
二、平行线
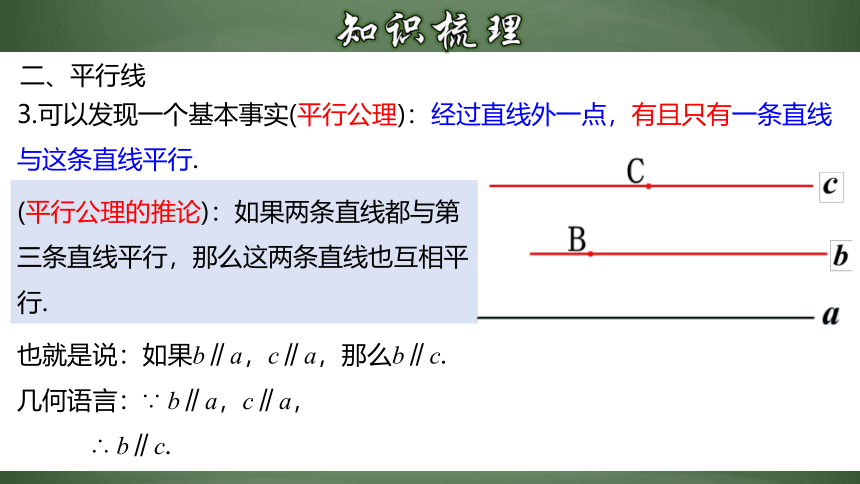
3.可以发现一个基本事实(平行公理):经过直线外一点,有且只有一条直线与这条直线平行.
(平行公理的推论):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
也就是说:如果b∥a,c∥a,那么b∥c.
几何语言:∵ b∥a,c∥a,
∴ b∥c.
二、平行线
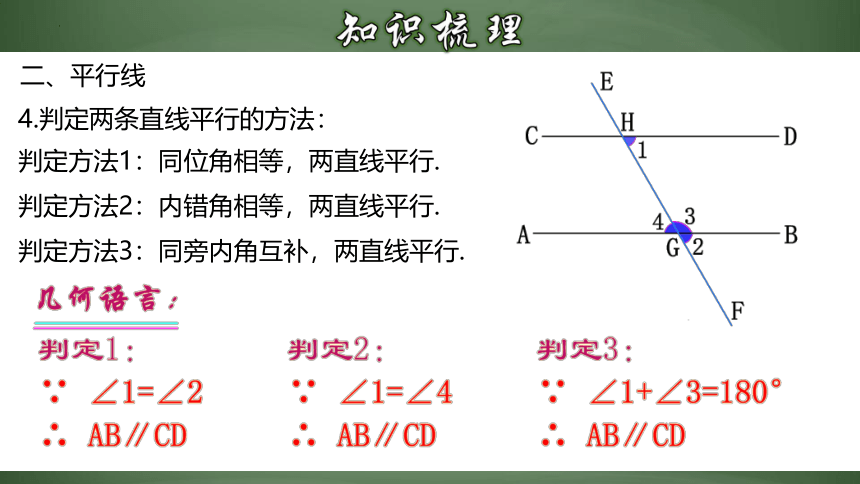
判定方法1:同位角相等,两直线平行.
判定方法2:内错角相等,两直线平行.
判定方法3:同旁内角互补,两直线平行.
4.判定两条直线平行的方法:
二、平行线
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
★命题的定义:判定一件事情的语句,叫做命题。
★命题的构成:命题由题设和结论组成。题设是已知项,结论是由已知项推出的事项.
★命题的书写形式
数学中的命题常可以写成“如果……那么……”的形式,这时“如果”后接的部分是题设,“那么”后接的部分是结论.
三、命题、定理、证明
★命题的分类
真命题:如果题设成立,那么结论一定成立,这样的命题叫做真命题.
假命题:如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
★定理的概念:一些命题的正确性是经过推理证实的,这样得到的真命题叫做定理.
★证明的概念:一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
三、命题、定理、证明
四、平移
1. 平移的定义:“三要素”
一个图形、一个方向、一个距离.
2. 平移的性质:“四特征”
图形的形状和大小不改变;
对应点所连的线段平行(或在一条直线上)且相等;
对应线段平行(或在一条直线上)且相等;
对应角相等.
四、平移
3.平移作图的一般步骤:
平移作图是平移性质的应用,利用平移可以得到许多美丽的图案,在具体作
图时,应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
01
相交线的有关概念和性质
例1.如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下列结论中,正确的个数为( )
①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离.
A.1个 B.2个
C.3个 D.4个
B
例2.(1)若ED,BF被AB所截,则∠1与____是同位角;(2)若ED, BC被AF所截,则∠2与______是内错角;(3)∠1与∠2是AB和AF被______所截构成的______角;(4)∠B与∠4是_____和_____被BC所截构成的_______角.
∠B
∠3
DE
内错
同旁内
AB
AF
解:∵∠BOE=∠NOE,
∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON
=180°-40°=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
例3.如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
【1-1】下列各图中的∠1与∠2,__________是同位角.
(1)(2)(3)
【1-2】已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm B.5cm C.小于2cm D.不大于2cm
D
【1-3】如图,按各组角的位置,判断错误的是( )
A.∠1与∠A是同旁内角 B.∠3与∠4是内错角
C.∠5与∠6是同旁内角 D.∠2与∠5是同位角
C
【1-4】如图,直线AB, CD相交于点O,若∠EOD=40°,
∠BOC=130°,那么射线OE与直线AB的位置关系
是____________.
OE⊥AB
【1-5】如图,直线AB、CD被EF所截,如果内错角∠1和∠2相等,那么同位角∠1和∠4相等吗 同旁内角∠1和∠3互补吗 请说明理由.
解:∠1=∠4,∠1和∠3互补.理由如下:
∵∠1=∠2,且∠2=∠4 (对顶角相等)
∴∠1=∠4
∵∠2+∠3=180°(邻补角定义)
∴∠1+∠3=180°
即∠1和∠3互补.
【1-6】如图,直线AB、CD相交于点O,OE平分,,且.求和的度数.
解:∵OE平分,,
∴,
又∵,
∴,
∵,
∴,
∴,
∴.
例4.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程,并填写理由或数学式:
解:∵∠3=∠4(已知),
∴AE //_____(________________________).
∴∠EDC=∠5(________________________).
∴∠5=∠A(已知),
∴∠EDC=______(__________).
∴DC//AB(_______________________).
∴∠5+∠ABC=180°(________________________),即∠5+∠2+∠3=180°
BC
内错角相等,两直线平行
两直线平行,内错角相等
∠A
等量代换
同位角相等,两直线平行
同旁内角互补,两直线平行
02
平行线的性质和判定
例4.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程,并填写理由或数学式:
∵∠1=∠2(已知),
∴∠5+∠1+∠3=180°(_________),
即∠BCF+∠3=180°.
∴BE//CF(_________________________).
等量代换
同旁内角互补,两直线平行
例5.如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A=∠F,为什么
解:∠AGB=∠DGF (对顶角相等)
∠AGB=∠EHF (已知)
∴∠DGF=∠EHF (等量代换)
∵BD//CE (同位角相等,两直线平行)
∴∠C=∠ABD (两直线平行,同位角相等)
∵∠C=∠D (已知)
∴∠D=∠ABD (等量代换)
∴AC//DF (内错角相等,两直线平行)
∴∠A=∠F (两直线平行,内错角相等)
例6.已知直线AB//CD,点M,N分别在直线AB,CD上,点P是平面内一个动点,且满足∠MPN=90°,过点N作射线NQ,使得∠PNQ=∠PNC.
(1)如图①,当射线NQ与NM重合,∠QND=50°时,则∠AMP=______;
25°
F
(2)如图②,当射线NQ与NM不重合,∠QND=α时,求∠AMP的度数(用含α的式子表示);
解:如图②,过P作PF//AB
∵AB//CD
∴AB//PF//CD
∴∠AMP=∠MPF , ∠CNP=∠FPN
∴∠MPN=∠AMP+∠PNC
∵∠MPN=90°
∴∠AMP+∠PNC=90°
∵∠PNQ=∠PNC,∠QND=α
∴∠PNC==90°-α.
∴∠AMP=90°-90°+α=α
(3)请直接写出在点P运动的过程中,∠QND与∠AMP之间的数量关系
____________________.
∠AMP=∠QND
【2-1】如图,AB//EF ,CD⊥EF,∠BAC=50°,则
∠ACD=( )
A.120° B.130° C.140° D.150°
【2-2】如图,将含有30°角的三角板的直角顶点放在
相互平行的两条直线其中一条上.若∠1=35°,则∠2的度数为( )
A.10° B.25° C.30° D.35°
C
D
【2-3】如图,AB//CD,则α, β, γ之间的等量关系为( )
A. α +β+ γ =360° B. α -β+ γ =180°
C. α +β- γ =180° D. α +β+ γ =180°
C
【2-4】如图,AB//CD,AE交CD于点F,点G在AB上,GH⊥BF,垂足为H,∠1=∠2,试说明AE⊥BF.请将下面的解答过程补充完整(填数字式子或理由).
解:∵AB//CD(已知),
∴∠1=______(________________________).
∵∠1=∠2(已知),
∴_____=______(_________).
∴______//_____(_______________________).
又∵GH⊥BF,即∠GHB=90°,
∴∠AFB=∠GHB=90°(______________________).
∴_____ ⊥ _____.
两直线平行,内错角相等
∠A
∠2 ∠A
等量代换
GH AE
同位角相等,两直线平行
两直线平行,同位角相等
AE BF
【2-5】如图,在三角形ABC中,CD是高,点E, F,G分别在BC,AB,AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
解:DG//BC.理由如下:
∵CD是三角形ABC的高,且EF⊥AB (已知)
∴∠BFE=∠BDC=90° (垂直定义)
∴EF//CD (同位角相等,两直线平行)
∴∠1=∠BCD (两直线平行,同位角相等)
∵∠1=∠2 (已知)
∴∠BCD=∠2 (等量代换)
∴DG//BC (内错角相等,两直线平行)
例7.指出下列命题的题设和结论,并把(3)写成“如果……,那么……”的形式.
(1)如果AB⊥CD,垂足为O,那么∠AOC=90°;
(2)如果∠1=∠2,2=∠3,那么∠1=∠3;
(3)两直线平行,同位角相等.
解:(1)题设:AB⊥CD,垂足为O,结论:∠AOC=90°;
(2)题设:∠1=∠2,2=∠3,结论:∠1=∠3;
(3)题设:两条平行线被第三条直线所截,结论:同位角相等.
如果两条平行线被第三条直线所截,那么同位角相等.
03
命题、定理、证明
例8.判断下列命题是真命题还是假命题.
(1)如果两个角互补,那么它们是邻补角;
(2)如果一个数能被2整除,那么它也能被4整除;
(3)相等的角是对顶角.
解:(1)假命题,反例:如图∠1=60°,∠2=120°,∠1与∠2互补,但它们不是邻补角.
例8.判断下列命题是真命题还是假命题.
(1)如果两个角互补,那么它们是邻补角;
(2)如果一个数能被2整除,那么它也能被4整除;
(3)相等的角是对顶角.
解:(2)假命题,反例:6能被2整除,但它不能被4整除.
(3)假命题,反例:如图,OC是∠AOB的平分线,
∠1=∠2,但它们不是对顶角.
【3-1】有下列语句:①画∠AOB的平分线;②直角都相等;③同旁内角互补吗 ④两点确定一条直线.其中命题的个数为( )
A.1 B.2 C.3 D.4
B
【3-2】对于同一平面内的三条直线a, b, c,给出下列5个论断:①a//b; ②b//c; ③a⊥b; ④a//c; ⑤a⊥c.以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
A.已知①②,则④ B.已知③⑤,则②
C.已知②④,则① D.已知①②,则⑤
D
【3-3】将下列命题写成“如果……,那么……”的形式.
(1)同旁内角互补,两直线平行;
(2)同角的补角相等;
(3)在同一平面内,垂直于同一条直线的两直线互相平行.
解: (1)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行;
(2)如果两个角是同一个角的补角,那么这两个角相等;
(3)在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线互相平行.
例9.如图,平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′.
分析:图形平移后的对应点有什么特征?作出点B和点C的对应点B′,C′,能确定三角形A′B′C′吗?
解:如图,连接AA′,
在l上截取BB′=AA′,则点B′就是点B的对应点.
过点B作AA′的平行线l,
进一步连接A′B′,B′C′,C′A′就得到平移后的三角形A′B′C′.
类似地,作出点C的对应点C′,
04
图形平移的性质及应用
例10.如图,每个小正方形的边长为1,在方格纸内△A′B′C′是将△ABC经过一次平移后得到的.根据下列条件,利用网格点和直尺画图:
(1)补全△ABC;
(2)作出中线CD;
(3)画出BC边上的高线AE;
(4)在平移过程中,线段AB扫过的
面积为 .
解:(1)如图所示,△ABC即为所求:
(2)如图所示,线段CD即为所求;
例10.如图,每个小正方形的边长为1,在方格纸内△A′B′C′是将△ABC经过一次平移后得到的.根据下列条件,利用网格点和直尺画图:
(3)画出BC边上的高线AE;
(4)在平移过程中,线段AB扫过的
面积为 .
解:(3)如图所示,线段AE即为所求;
(4),
∴.
即线段AB扫过的面积为16.
例11.南湖公园有很多的长方形草地,草地里修了很多有趣的小路,下面三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
①如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为 ;
②如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
③如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .
解:①将小路往左平移,直到E、F与A、B重合,
则平移后的四边形是一个矩形,并且,,
则草地的面积为:(平方米);
②将小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(平方米);
③将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:(米).
【4-1】下列四幅汽车标志设计中能用平移得到的是( )
A
【4-2】在5×5方格纸中,将图1中的图形N平移后的位置如图2中所示,那么正确的平移方法是( )
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
C
【4-3】在如图的方格纸中,画出将图中的三角形ABC向右平移5格后的三角形A1B1C1,然后再画出将三角形A1B1C1向上平移3格后的三角形A2B2C2.三角形A2B2C2是否可以看成是三角形ABC经过一次平移而得到的呢 如果可以,那么平移的方向和距离是什么
解:如图三角形A1B1C1,三角形A2B2C2为所求的图形;三角形A2B2C2可以看成是三角形ABC经过一次平移而得到的,平移方向是A到A2的方向,平移距离是线段AA2的长度.
【4-4】某酒店在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米的售价为40元,主楼梯道宽为3米,其侧面如图所示;铺设梯子的红地毯至少需要多长?花费至少多少元?
解:地毯的长度至少为:
(米);
(元).
答:铺设梯子的红地毯至少需要8.4米,花费至少1008元.
相交线与平行线 章节复习
1.进一步熟悉相交线所成的角及其基本结论;
2.进一步理解垂线、垂线段的概念及性质,点到直线的距离;
3.熟练掌握三线八角(同位角、内错角、同旁内角),两直线平行的判定及其应用;
4.熟练掌握平行线的性质及一些结论,并会应用;
5.平移的特征并会应用其解决问题.
1.邻补角:形如∠1与∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角.
2.对顶角:形如∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
性质:对顶角相等.
一、相交线
性质:邻补角互补.
3.垂直:当两条直线相交所构成的四个角中有一个是直角,我们就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线;互相垂直的两条直线的交点叫做垂足.
如右图,直线AB与直线CD垂直,
记作:AB⊥CD,垂足是O;
直线m与直线n垂直,
记作:m⊥n;
m
n
“⊥”是“垂直”的记号,读作“垂直于”;
而“┐”是图形中“垂直”(直角)的标记.
一、相交线
垂线的性质1:经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线.
即在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线
段的长度,叫做点到直线的距离.
一、相交线
一、相交线
两角的位置分别在直线AB,CD的同一方(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫做同位角.
4.三线八角:
两角的位置都在直线AB,CD之间,并且分别在直线EF两侧(∠3在直线EF左侧,∠5在直线EF右侧),具有这种位置关系的一对角叫做内错角.
两角的位置都在直线AB,CD之间,并且都在直线EF的同一旁(左侧),具有这种位置关系的一对角叫做同旁内角.
同位角、内错角、同旁内角的结构特征:
一、相交线
1.平行线定义:在同一个平面内,不相交的两条直线叫做平行线.
(在同一平面内,不重合的两条直线只有两种位置关系:相交和平行.)
2.表示法:通常用“∥”表示平行,读作“平行于”.
如下图中直线AB与直线CD平行,记作AB∥CD.
如果用l,m表示这两条直线,那么直线l与直线 m平行记作l∥m.
二、平行线
3.可以发现一个基本事实(平行公理):经过直线外一点,有且只有一条直线与这条直线平行.
(平行公理的推论):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
也就是说:如果b∥a,c∥a,那么b∥c.
几何语言:∵ b∥a,c∥a,
∴ b∥c.
二、平行线
判定方法1:同位角相等,两直线平行.
判定方法2:内错角相等,两直线平行.
判定方法3:同旁内角互补,两直线平行.
4.判定两条直线平行的方法:
二、平行线
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
★命题的定义:判定一件事情的语句,叫做命题。
★命题的构成:命题由题设和结论组成。题设是已知项,结论是由已知项推出的事项.
★命题的书写形式
数学中的命题常可以写成“如果……那么……”的形式,这时“如果”后接的部分是题设,“那么”后接的部分是结论.
三、命题、定理、证明
★命题的分类
真命题:如果题设成立,那么结论一定成立,这样的命题叫做真命题.
假命题:如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
★定理的概念:一些命题的正确性是经过推理证实的,这样得到的真命题叫做定理.
★证明的概念:一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
三、命题、定理、证明
四、平移
1. 平移的定义:“三要素”
一个图形、一个方向、一个距离.
2. 平移的性质:“四特征”
图形的形状和大小不改变;
对应点所连的线段平行(或在一条直线上)且相等;
对应线段平行(或在一条直线上)且相等;
对应角相等.
四、平移
3.平移作图的一般步骤:
平移作图是平移性质的应用,利用平移可以得到许多美丽的图案,在具体作
图时,应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
01
相交线的有关概念和性质
例1.如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下列结论中,正确的个数为( )
①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离.
A.1个 B.2个
C.3个 D.4个
B
例2.(1)若ED,BF被AB所截,则∠1与____是同位角;(2)若ED, BC被AF所截,则∠2与______是内错角;(3)∠1与∠2是AB和AF被______所截构成的______角;(4)∠B与∠4是_____和_____被BC所截构成的_______角.
∠B
∠3
DE
内错
同旁内
AB
AF
解:∵∠BOE=∠NOE,
∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON
=180°-40°=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
例3.如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
【1-1】下列各图中的∠1与∠2,__________是同位角.
(1)(2)(3)
【1-2】已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm B.5cm C.小于2cm D.不大于2cm
D
【1-3】如图,按各组角的位置,判断错误的是( )
A.∠1与∠A是同旁内角 B.∠3与∠4是内错角
C.∠5与∠6是同旁内角 D.∠2与∠5是同位角
C
【1-4】如图,直线AB, CD相交于点O,若∠EOD=40°,
∠BOC=130°,那么射线OE与直线AB的位置关系
是____________.
OE⊥AB
【1-5】如图,直线AB、CD被EF所截,如果内错角∠1和∠2相等,那么同位角∠1和∠4相等吗 同旁内角∠1和∠3互补吗 请说明理由.
解:∠1=∠4,∠1和∠3互补.理由如下:
∵∠1=∠2,且∠2=∠4 (对顶角相等)
∴∠1=∠4
∵∠2+∠3=180°(邻补角定义)
∴∠1+∠3=180°
即∠1和∠3互补.
【1-6】如图,直线AB、CD相交于点O,OE平分,,且.求和的度数.
解:∵OE平分,,
∴,
又∵,
∴,
∵,
∴,
∴,
∴.
例4.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程,并填写理由或数学式:
解:∵∠3=∠4(已知),
∴AE //_____(________________________).
∴∠EDC=∠5(________________________).
∴∠5=∠A(已知),
∴∠EDC=______(__________).
∴DC//AB(_______________________).
∴∠5+∠ABC=180°(________________________),即∠5+∠2+∠3=180°
BC
内错角相等,两直线平行
两直线平行,内错角相等
∠A
等量代换
同位角相等,两直线平行
同旁内角互补,两直线平行
02
平行线的性质和判定
例4.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE//CF.完善下面的解答过程,并填写理由或数学式:
∵∠1=∠2(已知),
∴∠5+∠1+∠3=180°(_________),
即∠BCF+∠3=180°.
∴BE//CF(_________________________).
等量代换
同旁内角互补,两直线平行
例5.如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A=∠F,为什么
解:∠AGB=∠DGF (对顶角相等)
∠AGB=∠EHF (已知)
∴∠DGF=∠EHF (等量代换)
∵BD//CE (同位角相等,两直线平行)
∴∠C=∠ABD (两直线平行,同位角相等)
∵∠C=∠D (已知)
∴∠D=∠ABD (等量代换)
∴AC//DF (内错角相等,两直线平行)
∴∠A=∠F (两直线平行,内错角相等)
例6.已知直线AB//CD,点M,N分别在直线AB,CD上,点P是平面内一个动点,且满足∠MPN=90°,过点N作射线NQ,使得∠PNQ=∠PNC.
(1)如图①,当射线NQ与NM重合,∠QND=50°时,则∠AMP=______;
25°
F
(2)如图②,当射线NQ与NM不重合,∠QND=α时,求∠AMP的度数(用含α的式子表示);
解:如图②,过P作PF//AB
∵AB//CD
∴AB//PF//CD
∴∠AMP=∠MPF , ∠CNP=∠FPN
∴∠MPN=∠AMP+∠PNC
∵∠MPN=90°
∴∠AMP+∠PNC=90°
∵∠PNQ=∠PNC,∠QND=α
∴∠PNC==90°-α.
∴∠AMP=90°-90°+α=α
(3)请直接写出在点P运动的过程中,∠QND与∠AMP之间的数量关系
____________________.
∠AMP=∠QND
【2-1】如图,AB//EF ,CD⊥EF,∠BAC=50°,则
∠ACD=( )
A.120° B.130° C.140° D.150°
【2-2】如图,将含有30°角的三角板的直角顶点放在
相互平行的两条直线其中一条上.若∠1=35°,则∠2的度数为( )
A.10° B.25° C.30° D.35°
C
D
【2-3】如图,AB//CD,则α, β, γ之间的等量关系为( )
A. α +β+ γ =360° B. α -β+ γ =180°
C. α +β- γ =180° D. α +β+ γ =180°
C
【2-4】如图,AB//CD,AE交CD于点F,点G在AB上,GH⊥BF,垂足为H,∠1=∠2,试说明AE⊥BF.请将下面的解答过程补充完整(填数字式子或理由).
解:∵AB//CD(已知),
∴∠1=______(________________________).
∵∠1=∠2(已知),
∴_____=______(_________).
∴______//_____(_______________________).
又∵GH⊥BF,即∠GHB=90°,
∴∠AFB=∠GHB=90°(______________________).
∴_____ ⊥ _____.
两直线平行,内错角相等
∠A
∠2 ∠A
等量代换
GH AE
同位角相等,两直线平行
两直线平行,同位角相等
AE BF
【2-5】如图,在三角形ABC中,CD是高,点E, F,G分别在BC,AB,AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
解:DG//BC.理由如下:
∵CD是三角形ABC的高,且EF⊥AB (已知)
∴∠BFE=∠BDC=90° (垂直定义)
∴EF//CD (同位角相等,两直线平行)
∴∠1=∠BCD (两直线平行,同位角相等)
∵∠1=∠2 (已知)
∴∠BCD=∠2 (等量代换)
∴DG//BC (内错角相等,两直线平行)
例7.指出下列命题的题设和结论,并把(3)写成“如果……,那么……”的形式.
(1)如果AB⊥CD,垂足为O,那么∠AOC=90°;
(2)如果∠1=∠2,2=∠3,那么∠1=∠3;
(3)两直线平行,同位角相等.
解:(1)题设:AB⊥CD,垂足为O,结论:∠AOC=90°;
(2)题设:∠1=∠2,2=∠3,结论:∠1=∠3;
(3)题设:两条平行线被第三条直线所截,结论:同位角相等.
如果两条平行线被第三条直线所截,那么同位角相等.
03
命题、定理、证明
例8.判断下列命题是真命题还是假命题.
(1)如果两个角互补,那么它们是邻补角;
(2)如果一个数能被2整除,那么它也能被4整除;
(3)相等的角是对顶角.
解:(1)假命题,反例:如图∠1=60°,∠2=120°,∠1与∠2互补,但它们不是邻补角.
例8.判断下列命题是真命题还是假命题.
(1)如果两个角互补,那么它们是邻补角;
(2)如果一个数能被2整除,那么它也能被4整除;
(3)相等的角是对顶角.
解:(2)假命题,反例:6能被2整除,但它不能被4整除.
(3)假命题,反例:如图,OC是∠AOB的平分线,
∠1=∠2,但它们不是对顶角.
【3-1】有下列语句:①画∠AOB的平分线;②直角都相等;③同旁内角互补吗 ④两点确定一条直线.其中命题的个数为( )
A.1 B.2 C.3 D.4
B
【3-2】对于同一平面内的三条直线a, b, c,给出下列5个论断:①a//b; ②b//c; ③a⊥b; ④a//c; ⑤a⊥c.以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
A.已知①②,则④ B.已知③⑤,则②
C.已知②④,则① D.已知①②,则⑤
D
【3-3】将下列命题写成“如果……,那么……”的形式.
(1)同旁内角互补,两直线平行;
(2)同角的补角相等;
(3)在同一平面内,垂直于同一条直线的两直线互相平行.
解: (1)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行;
(2)如果两个角是同一个角的补角,那么这两个角相等;
(3)在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线互相平行.
例9.如图,平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′.
分析:图形平移后的对应点有什么特征?作出点B和点C的对应点B′,C′,能确定三角形A′B′C′吗?
解:如图,连接AA′,
在l上截取BB′=AA′,则点B′就是点B的对应点.
过点B作AA′的平行线l,
进一步连接A′B′,B′C′,C′A′就得到平移后的三角形A′B′C′.
类似地,作出点C的对应点C′,
04
图形平移的性质及应用
例10.如图,每个小正方形的边长为1,在方格纸内△A′B′C′是将△ABC经过一次平移后得到的.根据下列条件,利用网格点和直尺画图:
(1)补全△ABC;
(2)作出中线CD;
(3)画出BC边上的高线AE;
(4)在平移过程中,线段AB扫过的
面积为 .
解:(1)如图所示,△ABC即为所求:
(2)如图所示,线段CD即为所求;
例10.如图,每个小正方形的边长为1,在方格纸内△A′B′C′是将△ABC经过一次平移后得到的.根据下列条件,利用网格点和直尺画图:
(3)画出BC边上的高线AE;
(4)在平移过程中,线段AB扫过的
面积为 .
解:(3)如图所示,线段AE即为所求;
(4),
∴.
即线段AB扫过的面积为16.
例11.南湖公园有很多的长方形草地,草地里修了很多有趣的小路,下面三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
①如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为 ;
②如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
③如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .
解:①将小路往左平移,直到E、F与A、B重合,
则平移后的四边形是一个矩形,并且,,
则草地的面积为:(平方米);
②将小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(平方米);
③将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:(米).
【4-1】下列四幅汽车标志设计中能用平移得到的是( )
A
【4-2】在5×5方格纸中,将图1中的图形N平移后的位置如图2中所示,那么正确的平移方法是( )
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
C
【4-3】在如图的方格纸中,画出将图中的三角形ABC向右平移5格后的三角形A1B1C1,然后再画出将三角形A1B1C1向上平移3格后的三角形A2B2C2.三角形A2B2C2是否可以看成是三角形ABC经过一次平移而得到的呢 如果可以,那么平移的方向和距离是什么
解:如图三角形A1B1C1,三角形A2B2C2为所求的图形;三角形A2B2C2可以看成是三角形ABC经过一次平移而得到的,平移方向是A到A2的方向,平移距离是线段AA2的长度.
【4-4】某酒店在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米的售价为40元,主楼梯道宽为3米,其侧面如图所示;铺设梯子的红地毯至少需要多长?花费至少多少元?
解:地毯的长度至少为:
(米);
(元).
答:铺设梯子的红地毯至少需要8.4米,花费至少1008元.
