2022-2023学年苏科版七年级数学下册 7.2探索平行线的性质 课件 (共38张PPT)
文档属性
| 名称 | 2022-2023学年苏科版七年级数学下册 7.2探索平行线的性质 课件 (共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-27 00:00:00 | ||
图片预览







文档简介
(共38张PPT)
探索平行线的性质
Explore the properties of parallel lines
苏科版七年级下册第7章平面图形的认识(二)
教学目标
01
掌握平行线的三个性质,区分判定与性质
03
掌握基本的平行线模型
02
综合运用平行线的性质定理进行简单的证明与计算
平行线的性质
01
复习引入
Q1:平行线的判定方法有哪些?
一、同位角相等,两直线平行。
二、内错角相等,两直线平行。
三、同旁内角互补,两直线平行。
Q2:反过来,如果两直线平行,那么同位角、内错角、同旁内角各有怎样的数量关系呢?
01
复习引入
Q3:画两条平行线AB、CD,再画直线EF,使EF与AB、CD相交,
并指出图中的同位角、内错角、同旁内角
A
B
C
D
E
F
1
2
3
4
5
6
7
8
同位角
∠1与∠2、∠3与∠4、
∠5与∠6、∠7与∠8
内错角
∠2与∠7、∠4与∠5
同旁内角
∠2与∠5、∠4与∠7
01
复习引入
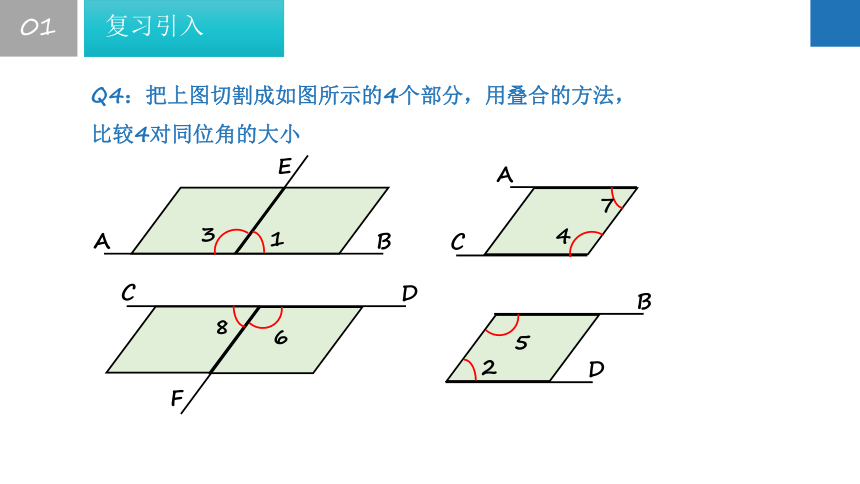
Q4:把上图切割成如图所示的4个部分,用叠合的方法,
比较4对同位角的大小
A
B
E
1
3
A
C
4
7
C
D
F
6
8
B
D
2
5
01
复习引入
A
B
E
1
3
C
D
F
6
8
A
C
4
7
B
D
2
5
B
D
2
5
A
C
4
7
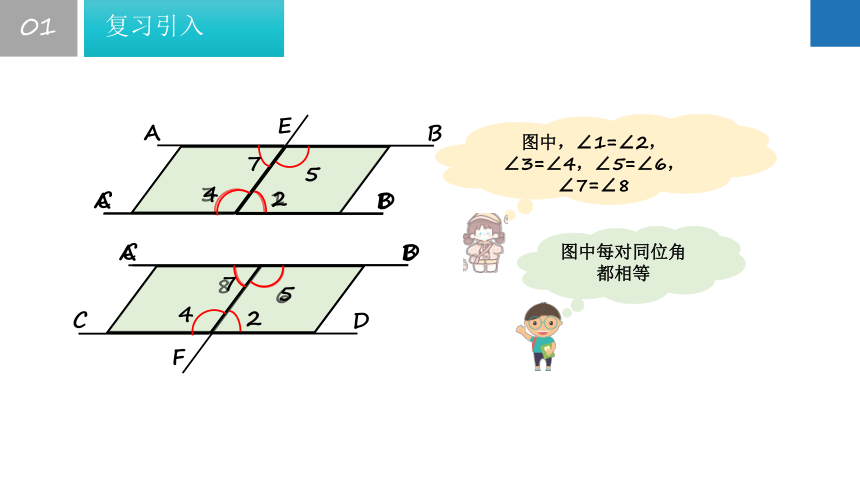
图中,∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8
图中每对同位角都相等
平行线的性质(一)
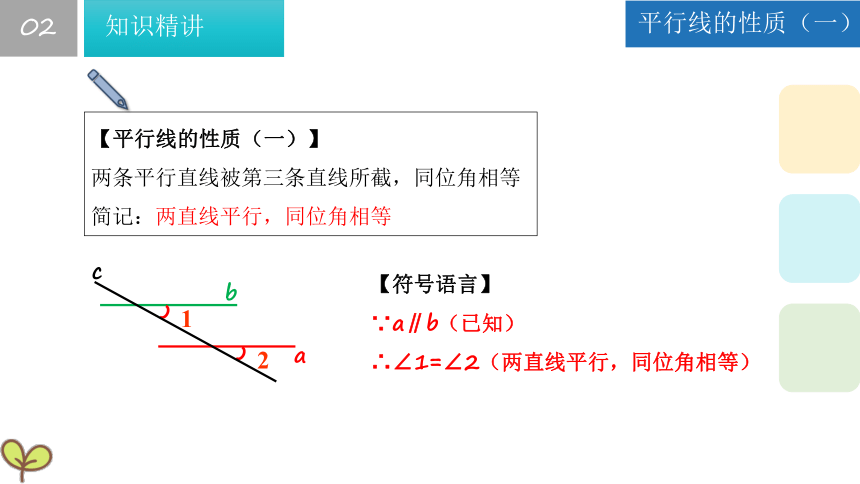
【平行线的性质(一)】
两条平行直线被第三条直线所截,同位角相等
简记:两直线平行,同位角相等
a
b
2
1
c
【符号语言】
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
02
知识精讲
01
复习引入
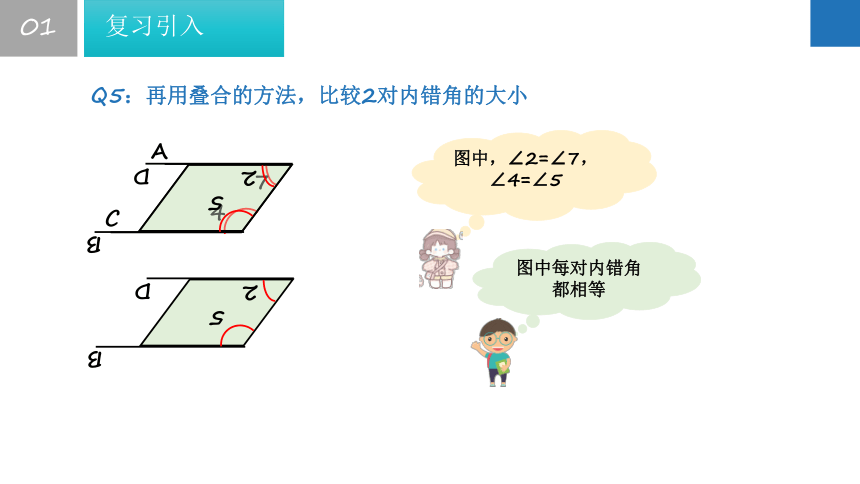
Q5:再用叠合的方法,比较2对内错角的大小
A
C
4
7
B
D
2
5
B
D
2
5
图中,∠2=∠7,∠4=∠5
图中每对内错角都相等
01
复习引入
Q6:如图,将∠4、∠7,∠2、∠5剪开,再拼在一起,
由此可以发现2对同旁内角之间有怎样的数量关系
A
7
D
2
B
5
C
4
A
7
C
4
D
2
B
5
图中,∠4+∠7=180°,∠2+∠5=180°
图中每对同旁内角都互补
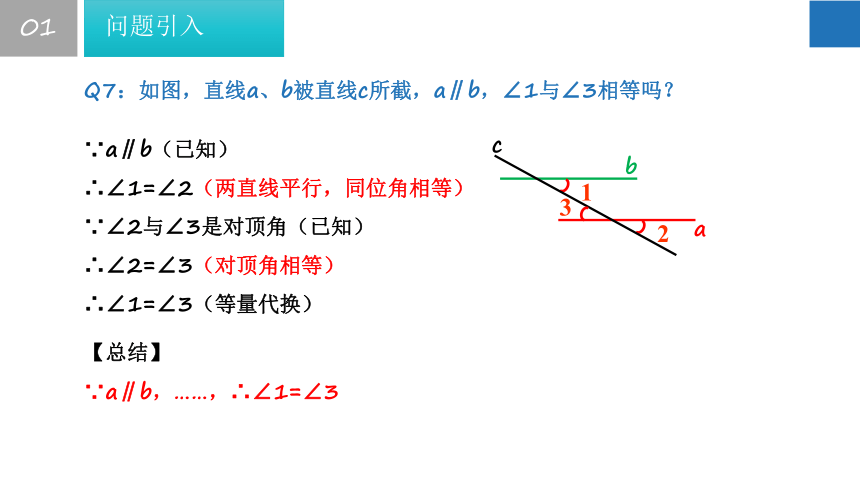
Q7:如图,直线a、b被直线c所截,a∥b,∠1与∠3相等吗?
a
b
2
1
c
3
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠2与∠3是对顶角(已知)
∴∠2=∠3(对顶角相等)
∴∠1=∠3(等量代换)
【总结】
∵a∥b,……,∴∠1=∠3
01
问题引入
Q8:如图,直线a、b被直线c所截,a∥b,∠1与之间有怎样的数量关系?
a
b
2
1
c
4
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠2+∠4=180°(邻补角的定义)
∴∠1+∠4=180°(等量代换)
【总结】
∵a∥b,……,∴∠1+∠4=180°
01
问题引入
平行线的性质(二)
【平行线的性质(二)】
两条平行直线被第三条直线所截,内错角相等
简记:两直线平行,内错角相等
a
b
1
c
3
【符号语言】
∵a∥b(已知)
∴∠1=∠3(两直线平行,内错角相等)
02
知识精讲
平行线的性质(三)
【平行线的性质(三)】
两条平行直线被第三条直线所截,同旁内角互补
简记:两直线平行,同旁内角互补
a
b
1
c
4
02
知识精讲
【符号语言】
∵a∥b(已知)
∴∠1+∠4=180°(两直线平行,同旁内角互补)
平行线的性质总结
【平行线的性质总结】
一、两直线平行,同位角相等。
二、两直线平行,内错角相等。
三、两直线平行,同旁内角互补。
02
知识精讲
例1、如图,AB∥EC,则下列结论正确的是( )
A.∠A=∠ECD B.∠A=∠ACE C.∠B=∠ACE D.∠B=∠ACB
B
【平行线的性质】
例2、如图,下列判断中正确的是( )
A.如果EF∥GH,那么∠4+∠3=180°
B.如果AB∥CD,那么∠1+∠4=180°
C.如果AB∥CD,那么∠1=∠2
D.如果AB∥CD,那么∠2=∠3
C
【分析】
A.如果EF∥GH,那么∠4+∠1=180°,×;
B.如果AB∥CD,那么∠3+∠4=180°,×;
C.如果AB∥CD,那么∠1=∠2,√;
D.如果EF∥GH,那么∠2=∠3,×.
例3、将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1)∠1=∠2,(2)∠1=∠3,(3)∠2+∠4=90°,(4)∠4+∠5=180°.
其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】
(1)∠1和∠2是两平行线间的同位角,∴∠1=∠2;
(2)∠1和∠3不属于平行线间的同位角或内错角,∴∠1和∠3不一定相等;
(3)∠2、∠4和直角三角板的直角组成一个平角180°,∴∠2+∠4=90°;
(4)∠4和∠5是两平行线间的同旁内角,∴∠4+∠5=180°.
C
例4、如图,已知AB∥CD,BC是∠ABD的平分线,若∠3=100°,则∠2的度数为( )
A.40° B.50° C.60° D.80°
B
【分析】
∵AB∥CD,∠3=100°
∴∠ABD=∠3=100°
∵BC是∠ABD的平分线
∴∠2=∠1=∠ABD=50°
例4、如图,在△ABC中,AB=AC,∠B=66°,D,E分别为AB,BC上一点,AF∥DE,若∠BDE=30°,则∠FAC的度数为_________.
【分析】
∵AB=AC,∠B=66°
∴∠C=66°
∴∠BAC=48°
∵AF∥DE,∠BDE=30°
∴∠BAF=∠BDE=30°
∴∠FAC=18°
18°
例5、如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
证明:
∵AD∥BC(已知)
∴∠B=∠EAD(两直线平行,同位角相等)
∠DAC=∠C(两直线平行,内错角相等)
又∵∠B=∠C(已知)
∴∠EAD=∠DAC(等量代换)
∴AD平分∠CAE(角平分线的定义)
例6、如图,点C、D在线段AB上,且AM∥NB.下列结论中一定正确的是( )
①若∠AMD=∠CNB,则∠BDM=∠ACN;
②若∠AMD=∠CNB,则AN∥MB;
③若CN∥MD,则∠BMD=∠ANC;
④若AN∥MB,则∠MAN=∠MBN.
A.①③ B.①④ C.②③ D.②④
【平行线的判定与性质】
【分析】
①∵AM∥NB,∴∠MAB=∠ABN,
∵∠AMD=∠CNB,∴∠ADM=∠BCN,即∠BDM=∠ACN,∴√;
②由AM∥NB,∠AMD=∠CNB,推不出AN∥MB,∴×;
③由AM∥NB,CN∥MD,推不出∠BMD=∠ANC,∴×;
④∵AN∥MB,∴∠BAN=∠ABM,
∴∠BAN+∠MAB=∠ABM+∠ABN,即∠MAN=∠MBN,∴√.
B
例7、如图,△ABC中,FG∥CD,DE平分∠ADC,∠1+∠2=180°,
求证:∠1=∠B.
证明:∵FG∥CD(已知),
∴∠2+∠3=180° (两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1=∠3 (同角的补角相等),
∵DE平分∠ADC(已知),
∴∠1=∠4 (角平分线的定义),
∴∠3=∠4 (等量代换),
∴DE∥BC(内错角相等,两直线平行),
∴∠1=∠B (两直线平行,同位角相等).
平行线模型
01
问题引入
Q1:如图, AB∥CD ,探索下图中∠P与∠B、∠D的关系,画出辅助线并证明.
证明:过点P作AB的平行线PQ
∵AB∥PQ(已知)
∴∠B+∠1=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴PQ∥CD(平行线的传递性)
∴∠D+∠2=180°(两直线平行,同旁内角互补)
∴∠B+∠D+∠1+∠2=360°(等式的性质)
又∵∠P=∠1+∠2(等量代换)
∴∠B+∠D+∠P=360°(等量代换)
1
2
子弹模型
Q
Q2:如图, AB∥CD ,探索下图中∠P与∠B、∠D的关系,画出辅助线并证明.
证明:过点P作AB的平行线PQ
∵AB∥PQ(已知)
∴∠B=∠1(两直线平行,内错角相等)
∵AB∥CD(已知)
∴PQ∥CD(平行线的传递性)
∴∠D=∠2(两直线平行,内错角相等)
又∵∠P=∠1+∠2(等量代换)
∴∠P=∠B+∠D(等量代换)
1
2
猪手模型
01
问题引入
Q
Q3:如图, AB∥CD ,探索下图中∠1与∠2、∠3的关系,画出辅助线并证明.
证明:过点E作AB的平行线EF
∵AB∥EF(已知)
∴∠1+∠4=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴CD∥EF(平行线的传递性)
∴∠3+∠2+∠4=180°(两直线平行,同旁内角互补)
∴∠1=∠2+∠3(等量代换)
01
问题引入
4
F
拐角模型(一)
Q4:如图, AB∥CD ,探索下图中∠1与∠2、∠3的关系,画出辅助线并证明.
证明:过点E作AB的平行线EF
∵AB∥EF(已知)
∴∠1=∠4(两直线平行,内错角相等)
∵AB∥CD(已知)
∴CD∥EF(平行线的传递性)
∴∠3=∠4+∠2(两直线平行,内错角相等)
∴∠3=∠1+∠2(等量代换)
01
问题引入
拐角模型(二)
F
4
子弹模型与猪手模型
02
知识精讲
子弹模型:
∠1+∠2+∠3=360°
猪手模型:
∠2=∠1+∠3
拐角模型
02
知识精讲
拐角模型(一):
∠1=∠2+∠3
拐角模型(二):
∠3=∠1+∠2
例8、如图,已知a∥b,∠1=120°,∠2=90°,则∠3的度数是( )
A.120° B.130° C.140° D.150°
【分析】
子弹模型:∠1+∠2+∠3=360°
D
【子弹模型】
例9、如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
A.100° B.120° C.140° D.90°
【分析】
子弹模型:∠B+∠C+∠D=360°
B
例10、如图,直线a∥b,∠P=75°,∠2=30°,则∠1=________.
【分析】
猪手模型:∠P=∠1+∠2
45°
【猪手模型】
例11、如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=30°,则∠2=________.
【分析】
猪手模型:∠2=90°+∠1
120°
例12、如图,AB∥CD,∠C=75°,∠E=35°,则∠A为( )
A.90° B.35° C.40° D.75°
C
【拐角模型】
【分析】
拐角模型(二):∠C=∠A+∠E
例13、如图,已知FD∥BE,则∠1-∠A+∠2等于( )
A.90° B.135° C.150° D.180°
D
【分析】过点A作FD的平行线AG
∵AG∥FD(已知)
∴∠1+∠3=180°(两直线平行,同旁内角互补)
∵FD∥BE(已知)
∴AG∥BE(平行线的传递性)
∴∠2=∠BAC+∠3(两直线平行,内错角相等)
∴∠3=∠2-∠BAC(等式的性质)
∴∠1+∠2-∠BAC=180°,即∠1-∠BAC+∠2=180°(等量代换)
G
3
课后总结
【平行线的性质总结】
一、两直线平行,同位角相等。
二、两直线平行,内错角相等。
三、两直线平行,同旁内角互补。
子弹模型:∠1+∠2+∠3=360°
猪手模型:∠2=∠1+∠3
拐角模型(一):
∠1=∠2+∠3
拐角模型(二):
∠3=∠1+∠2
谢谢学习
Thank you for learning
探索平行线的性质
Explore the properties of parallel lines
苏科版七年级下册第7章平面图形的认识(二)
教学目标
01
掌握平行线的三个性质,区分判定与性质
03
掌握基本的平行线模型
02
综合运用平行线的性质定理进行简单的证明与计算
平行线的性质
01
复习引入
Q1:平行线的判定方法有哪些?
一、同位角相等,两直线平行。
二、内错角相等,两直线平行。
三、同旁内角互补,两直线平行。
Q2:反过来,如果两直线平行,那么同位角、内错角、同旁内角各有怎样的数量关系呢?
01
复习引入
Q3:画两条平行线AB、CD,再画直线EF,使EF与AB、CD相交,
并指出图中的同位角、内错角、同旁内角
A
B
C
D
E
F
1
2
3
4
5
6
7
8
同位角
∠1与∠2、∠3与∠4、
∠5与∠6、∠7与∠8
内错角
∠2与∠7、∠4与∠5
同旁内角
∠2与∠5、∠4与∠7
01
复习引入
Q4:把上图切割成如图所示的4个部分,用叠合的方法,
比较4对同位角的大小
A
B
E
1
3
A
C
4
7
C
D
F
6
8
B
D
2
5
01
复习引入
A
B
E
1
3
C
D
F
6
8
A
C
4
7
B
D
2
5
B
D
2
5
A
C
4
7
图中,∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8
图中每对同位角都相等
平行线的性质(一)
【平行线的性质(一)】
两条平行直线被第三条直线所截,同位角相等
简记:两直线平行,同位角相等
a
b
2
1
c
【符号语言】
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
02
知识精讲
01
复习引入
Q5:再用叠合的方法,比较2对内错角的大小
A
C
4
7
B
D
2
5
B
D
2
5
图中,∠2=∠7,∠4=∠5
图中每对内错角都相等
01
复习引入
Q6:如图,将∠4、∠7,∠2、∠5剪开,再拼在一起,
由此可以发现2对同旁内角之间有怎样的数量关系
A
7
D
2
B
5
C
4
A
7
C
4
D
2
B
5
图中,∠4+∠7=180°,∠2+∠5=180°
图中每对同旁内角都互补
Q7:如图,直线a、b被直线c所截,a∥b,∠1与∠3相等吗?
a
b
2
1
c
3
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠2与∠3是对顶角(已知)
∴∠2=∠3(对顶角相等)
∴∠1=∠3(等量代换)
【总结】
∵a∥b,……,∴∠1=∠3
01
问题引入
Q8:如图,直线a、b被直线c所截,a∥b,∠1与之间有怎样的数量关系?
a
b
2
1
c
4
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠2+∠4=180°(邻补角的定义)
∴∠1+∠4=180°(等量代换)
【总结】
∵a∥b,……,∴∠1+∠4=180°
01
问题引入
平行线的性质(二)
【平行线的性质(二)】
两条平行直线被第三条直线所截,内错角相等
简记:两直线平行,内错角相等
a
b
1
c
3
【符号语言】
∵a∥b(已知)
∴∠1=∠3(两直线平行,内错角相等)
02
知识精讲
平行线的性质(三)
【平行线的性质(三)】
两条平行直线被第三条直线所截,同旁内角互补
简记:两直线平行,同旁内角互补
a
b
1
c
4
02
知识精讲
【符号语言】
∵a∥b(已知)
∴∠1+∠4=180°(两直线平行,同旁内角互补)
平行线的性质总结
【平行线的性质总结】
一、两直线平行,同位角相等。
二、两直线平行,内错角相等。
三、两直线平行,同旁内角互补。
02
知识精讲
例1、如图,AB∥EC,则下列结论正确的是( )
A.∠A=∠ECD B.∠A=∠ACE C.∠B=∠ACE D.∠B=∠ACB
B
【平行线的性质】
例2、如图,下列判断中正确的是( )
A.如果EF∥GH,那么∠4+∠3=180°
B.如果AB∥CD,那么∠1+∠4=180°
C.如果AB∥CD,那么∠1=∠2
D.如果AB∥CD,那么∠2=∠3
C
【分析】
A.如果EF∥GH,那么∠4+∠1=180°,×;
B.如果AB∥CD,那么∠3+∠4=180°,×;
C.如果AB∥CD,那么∠1=∠2,√;
D.如果EF∥GH,那么∠2=∠3,×.
例3、将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1)∠1=∠2,(2)∠1=∠3,(3)∠2+∠4=90°,(4)∠4+∠5=180°.
其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】
(1)∠1和∠2是两平行线间的同位角,∴∠1=∠2;
(2)∠1和∠3不属于平行线间的同位角或内错角,∴∠1和∠3不一定相等;
(3)∠2、∠4和直角三角板的直角组成一个平角180°,∴∠2+∠4=90°;
(4)∠4和∠5是两平行线间的同旁内角,∴∠4+∠5=180°.
C
例4、如图,已知AB∥CD,BC是∠ABD的平分线,若∠3=100°,则∠2的度数为( )
A.40° B.50° C.60° D.80°
B
【分析】
∵AB∥CD,∠3=100°
∴∠ABD=∠3=100°
∵BC是∠ABD的平分线
∴∠2=∠1=∠ABD=50°
例4、如图,在△ABC中,AB=AC,∠B=66°,D,E分别为AB,BC上一点,AF∥DE,若∠BDE=30°,则∠FAC的度数为_________.
【分析】
∵AB=AC,∠B=66°
∴∠C=66°
∴∠BAC=48°
∵AF∥DE,∠BDE=30°
∴∠BAF=∠BDE=30°
∴∠FAC=18°
18°
例5、如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
证明:
∵AD∥BC(已知)
∴∠B=∠EAD(两直线平行,同位角相等)
∠DAC=∠C(两直线平行,内错角相等)
又∵∠B=∠C(已知)
∴∠EAD=∠DAC(等量代换)
∴AD平分∠CAE(角平分线的定义)
例6、如图,点C、D在线段AB上,且AM∥NB.下列结论中一定正确的是( )
①若∠AMD=∠CNB,则∠BDM=∠ACN;
②若∠AMD=∠CNB,则AN∥MB;
③若CN∥MD,则∠BMD=∠ANC;
④若AN∥MB,则∠MAN=∠MBN.
A.①③ B.①④ C.②③ D.②④
【平行线的判定与性质】
【分析】
①∵AM∥NB,∴∠MAB=∠ABN,
∵∠AMD=∠CNB,∴∠ADM=∠BCN,即∠BDM=∠ACN,∴√;
②由AM∥NB,∠AMD=∠CNB,推不出AN∥MB,∴×;
③由AM∥NB,CN∥MD,推不出∠BMD=∠ANC,∴×;
④∵AN∥MB,∴∠BAN=∠ABM,
∴∠BAN+∠MAB=∠ABM+∠ABN,即∠MAN=∠MBN,∴√.
B
例7、如图,△ABC中,FG∥CD,DE平分∠ADC,∠1+∠2=180°,
求证:∠1=∠B.
证明:∵FG∥CD(已知),
∴∠2+∠3=180° (两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1=∠3 (同角的补角相等),
∵DE平分∠ADC(已知),
∴∠1=∠4 (角平分线的定义),
∴∠3=∠4 (等量代换),
∴DE∥BC(内错角相等,两直线平行),
∴∠1=∠B (两直线平行,同位角相等).
平行线模型
01
问题引入
Q1:如图, AB∥CD ,探索下图中∠P与∠B、∠D的关系,画出辅助线并证明.
证明:过点P作AB的平行线PQ
∵AB∥PQ(已知)
∴∠B+∠1=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴PQ∥CD(平行线的传递性)
∴∠D+∠2=180°(两直线平行,同旁内角互补)
∴∠B+∠D+∠1+∠2=360°(等式的性质)
又∵∠P=∠1+∠2(等量代换)
∴∠B+∠D+∠P=360°(等量代换)
1
2
子弹模型
Q
Q2:如图, AB∥CD ,探索下图中∠P与∠B、∠D的关系,画出辅助线并证明.
证明:过点P作AB的平行线PQ
∵AB∥PQ(已知)
∴∠B=∠1(两直线平行,内错角相等)
∵AB∥CD(已知)
∴PQ∥CD(平行线的传递性)
∴∠D=∠2(两直线平行,内错角相等)
又∵∠P=∠1+∠2(等量代换)
∴∠P=∠B+∠D(等量代换)
1
2
猪手模型
01
问题引入
Q
Q3:如图, AB∥CD ,探索下图中∠1与∠2、∠3的关系,画出辅助线并证明.
证明:过点E作AB的平行线EF
∵AB∥EF(已知)
∴∠1+∠4=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴CD∥EF(平行线的传递性)
∴∠3+∠2+∠4=180°(两直线平行,同旁内角互补)
∴∠1=∠2+∠3(等量代换)
01
问题引入
4
F
拐角模型(一)
Q4:如图, AB∥CD ,探索下图中∠1与∠2、∠3的关系,画出辅助线并证明.
证明:过点E作AB的平行线EF
∵AB∥EF(已知)
∴∠1=∠4(两直线平行,内错角相等)
∵AB∥CD(已知)
∴CD∥EF(平行线的传递性)
∴∠3=∠4+∠2(两直线平行,内错角相等)
∴∠3=∠1+∠2(等量代换)
01
问题引入
拐角模型(二)
F
4
子弹模型与猪手模型
02
知识精讲
子弹模型:
∠1+∠2+∠3=360°
猪手模型:
∠2=∠1+∠3
拐角模型
02
知识精讲
拐角模型(一):
∠1=∠2+∠3
拐角模型(二):
∠3=∠1+∠2
例8、如图,已知a∥b,∠1=120°,∠2=90°,则∠3的度数是( )
A.120° B.130° C.140° D.150°
【分析】
子弹模型:∠1+∠2+∠3=360°
D
【子弹模型】
例9、如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
A.100° B.120° C.140° D.90°
【分析】
子弹模型:∠B+∠C+∠D=360°
B
例10、如图,直线a∥b,∠P=75°,∠2=30°,则∠1=________.
【分析】
猪手模型:∠P=∠1+∠2
45°
【猪手模型】
例11、如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=30°,则∠2=________.
【分析】
猪手模型:∠2=90°+∠1
120°
例12、如图,AB∥CD,∠C=75°,∠E=35°,则∠A为( )
A.90° B.35° C.40° D.75°
C
【拐角模型】
【分析】
拐角模型(二):∠C=∠A+∠E
例13、如图,已知FD∥BE,则∠1-∠A+∠2等于( )
A.90° B.135° C.150° D.180°
D
【分析】过点A作FD的平行线AG
∵AG∥FD(已知)
∴∠1+∠3=180°(两直线平行,同旁内角互补)
∵FD∥BE(已知)
∴AG∥BE(平行线的传递性)
∴∠2=∠BAC+∠3(两直线平行,内错角相等)
∴∠3=∠2-∠BAC(等式的性质)
∴∠1+∠2-∠BAC=180°,即∠1-∠BAC+∠2=180°(等量代换)
G
3
课后总结
【平行线的性质总结】
一、两直线平行,同位角相等。
二、两直线平行,内错角相等。
三、两直线平行,同旁内角互补。
子弹模型:∠1+∠2+∠3=360°
猪手模型:∠2=∠1+∠3
拐角模型(一):
∠1=∠2+∠3
拐角模型(二):
∠3=∠1+∠2
谢谢学习
Thank you for learning
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
