2022-2023学年苏科版七年级数学下册 7.1探索直线平行的条件 课件 (共48张PPT)
文档属性
| 名称 | 2022-2023学年苏科版七年级数学下册 7.1探索直线平行的条件 课件 (共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 28.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-27 00:00:00 | ||
图片预览










文档简介
(共48张PPT)
探索直线平行的条件
Explore the condition for parallel lines
苏科版七年级下册第7章平面图形的认识(二)
教学目标
01
认识三线八角模型,并借助于三线八角模型理解同位角、内错角与同旁内角
02
区分同位角、内错角与同旁内角,并能根据对应的模型快速识别出这三类角
03
理解平行线的三种判定方法,并将其熟练应用于平行线的判断与证明当中去
三线八角与同位角
知识精讲
复习引入
01
平行
猴子最讨厌什么呢?
知识精讲
复习引入
01
Q1:什么是平行线?
在同一平面内,不相交的两条直线叫做平行线
如图,两条直线互相平行,记作a∥b或AB∥CD
C
a
b
D
A
B
知识精讲
复习引入
01
Q2:如何用直尺和三角尺画平行线?
放
移
画
a
a
b
画
a
知识精讲
问题引入
01
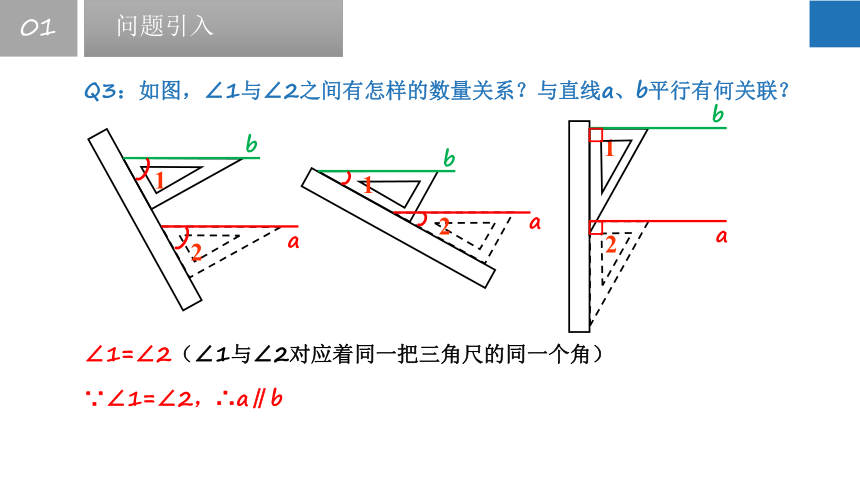
Q3:如图,∠1与∠2之间有怎样的数量关系?与直线a、b平行有何关联?
a
b
2
1
∠1=∠2(∠1与∠2对应着同一把三角尺的同一个角)
∵∠1=∠2,∴a∥b
a
b
2
1
1
a
b
2
知识精讲
问题引入
01
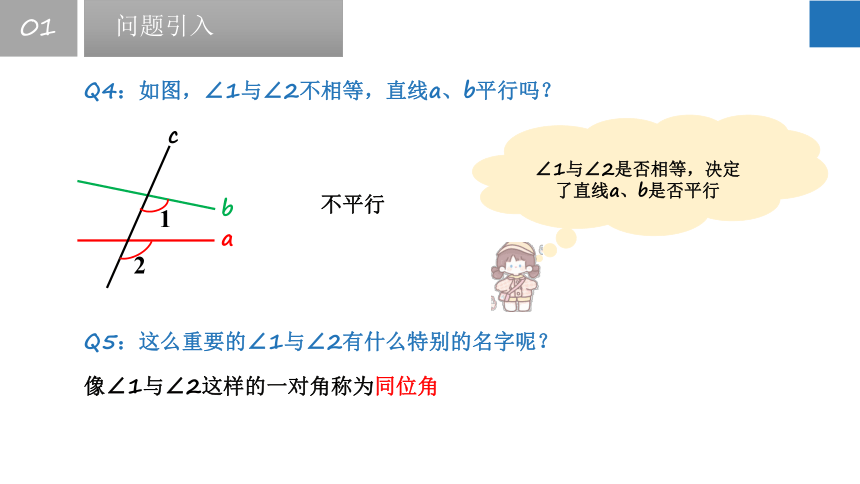
Q4:如图,∠1与∠2不相等,直线a、b平行吗?
a
b
c
2
1
不平行
∠1与∠2是否相等,决定了直线a、b是否平行
Q5:这么重要的∠1与∠2有什么特别的名字呢?
像∠1与∠2这样的一对角称为同位角
知识精讲
问题引入
01
Q6:两条直线a、b被第三条直线c所截成的角共有几个?
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
8个
被截直线
被截直线
截
线
同位角在被截线同侧
在截线同侧
问题引入
01
Q7:同位角与被截线、截线之间有何位置关系?
知识精讲
问题引入
01
Q8:同位角有几对?
4对
∠1与∠2
∠3与∠4
∠5与∠6
∠7与∠8
1
2
F型
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
02
知识精讲
【三线八角】
定义:直线a、b与c相交(两条直线a、b被第三条直线c所截)构成八个角
三线八角
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
02
知识精讲
【同位角】
定义:在被截线同侧,且在截线同侧的两个角
一个三线八角模型中有4对同位角
同位角
1
2
F型
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
02
知识精讲
平行线的判定(一)
【平行线的判定(一)】
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
简记:同位角相等,两直线平行
a
b
2
1
c
【符号语言】
∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
知识精讲
例1、如图,∠A的同位角是( )
A.∠BOE B.∠AOE C.∠BOD D.∠AOD
【同位角】
A
知识精讲
例2、若∠1与∠2的关系是同位角,∠1=30°,则∠2=( )
A.30° B.150° C.50°或130° D.不确定
D
【分析】
不要把“同位角”与“相等”画上等号!!!
知识精讲
例3、下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
C
知识精讲
例4、如图,下列图形中的∠1和∠2不是同位角的是( )
A. B.
C. D.
C
知识精讲
例5、如图,已知AB⊥BC,∠1+∠2=90°,∠2=∠3.求证:BE∥DF.
【平行线的判定】
证明:
∵AB⊥BC(已知),
∴∠ABC=90°(垂直的定义),
即∠3+∠4=90°(等量代换).
∵∠1+∠2=90°,且∠2=∠3(已知),
∴∠1+∠3=90°(等量代换),
∴∠1=∠4(等量代换),
∴BE∥DF(同位角相等,两直线平行).
内错角
Q1:如图,直线a、b被直线c所截,∠1=∠3,直线a与直线b平行吗?
a
b
2
1
c
3
只要说明同位角∠1、∠2相等,就可以知道a∥b了
∵∠2与∠3是对顶角(已知)
∴∠2=∠3(对顶角相等)
又∵∠1=∠3(已知)
∴∠1=∠2(等量代换)
∴a∥b(同位角相等,两直线平行)
∠2与∠3是对顶角,∠1=∠3
【总结】
∵∠1=∠3,……,∴a∥b
问题引入
01
知识精讲
问题引入
01
Q2:如图,∠1与∠3不相等,直线a、b平行吗?
不平行
∠1与∠3是否相等,决定了直线a、b是否平行
Q3:这么重要的∠1与∠3又有什么特别的名字呢?
像∠1与∠3这样的一对角称为内错角
a
b
1
c
3
内错角在被截线内侧
在截线两侧
问题引入
01
Q4:内错角与被截线、截线之间有何位置关系?
被截直线
被截直线
截
线
知识精讲
问题引入
01
Q5:一个三线八角模型中,内错角有几对?
2对
∠1与∠8
∠3与∠6
Z型
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
3
6
02
知识精讲
【内错角】
定义:在被截线内侧,且在截线两侧的两个角
一个三线八角模型中有2对内错角
内错角
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
Z型
3
6
02
知识精讲
平行线的判定(二)
【平行线的判定(二)】
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
简记:内错角相等,两直线平行
a
b
1
c
3
【符号语言】
∵∠1=∠3(已知)
∴a∥b(内错角相等,两直线平行)
知识精讲
例6、已知∠1与∠2是内错角,则( )
A.∠1=∠2 B.∠1+∠2=180°
C.∠1<∠2 D.以上都有可能
D
【内错角】
【分析】
不要把“内错角”与“相等”画上等号!!!
知识精讲
例7、如图,在∠1、∠2、∠3、∠4、∠5、∠6中,内错角有( )
A.1对 B.2对 C.3对 D.4对
C
【分析】
∵直线DC、直线DG被直线AB所截,
∴∠1和∠5是内错角,∠3和∠6是内错角;
∵直线AB、直线AC被直线DG所截,
∴∠2和∠4是内错角.
知识精讲
例8、如图,下列判断正确的是( )
A.∠5与∠3是内错角 B.∠2与∠4是同位角
C.∠3与∠6是同位角 D.∠2与∠5是对顶角
D
知识精讲
例9、如图,下列条件中可以判定DE∥AB的是( )
A.∠E=∠DCA B.∠E=∠DCE C.∠E=∠CDE D.∠E=∠BCE
D
【平行线的判定】
知识精讲
例10、下列图形中,由∠1=∠2,能得到AB∥CD的是( )
A. B.
C. D.
【分析】
选项C,∠1=∠2,根据“内错角相等,两直线平行”可得AC∥BD
A
知识精讲
例11、如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,证明AE∥GF.
证明:∵∠BAG+∠AGD=180°(已知),
∠AGC+∠AGD=180°(邻补角的定义),
∴∠BAG=∠AGC(同角的补角相等).
∵EA平分∠BAG,
∴∠1=∠BAG(角平分线的定义).
∵FG平分∠AGC,
∴∠2=∠AGC,
∴∠1=∠2(等量代换),
∴AE∥GF(内错角相等,两直线平行).
同旁内角
Q1:如图,直线a、b被直线c所截,∠1+∠4=180°,直线a与直线b平行吗?
a
b
2
1
c
4
∠1、∠2都是∠4的补角
∵∠1+∠4=180°(已知)
且∠2+∠4=180°(邻补角的定义)
∴∠1=∠2(等量代换)
∴a∥b(同位角相等,两直线平行)
【总结】
∵∠1+∠4=180°,……,∴a∥b
问题引入
01
知识精讲
问题引入
01
Q2:如图,∠1+∠4≠180°,直线a、b平行吗?
不平行
∠1+∠4是否为180°,决定了直线a、b是否平行
Q3:这么重要的∠1与∠4又有什么特别的名字呢?
像∠1与∠4这样的一对角称为同旁内角
a
b
1
c
4
同旁内角在被截线内侧
在截线同侧
问题引入
01
Q4:同旁内角与被截线、截线之间有何位置关系?
被截直线
被截直线
截
线
知识精讲
问题引入
01
Q5:一个三线八角模型中,同旁内角有几对?
2对
∠1与∠6
∠3与∠8
U型
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
1
6
02
知识精讲
【同旁内角】
定义:在被截线内侧,且在截线同侧的两个角
一个三线八角模型中有2对同旁内角
同旁内角
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
U型
1
6
02
知识精讲
平行线的判定(三)
【平行线的判定(三)】
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
简记:同旁内角互补,两直线平行
a
b
1
c
4
【符号语言】
∵∠1+∠4=180°(已知)
∴a∥b(同旁内角互补,两直线平行)
02
知识精讲
平行线的判定方法
【平行线的判定方法】
一、同位角相等,两直线平行。
二、内错角相等,两直线平行。
三、同旁内角互补,两直线平行。
知识精讲
例12、若∠1与∠2是同旁内角,则( )
A.∠1与∠2不可能相等 B.∠1与∠2一定互补
C.∠1与∠2可能互余 D.∠1与∠2一定相等
C
【同旁内角】
【分析】
不要把“同旁内角”与“互补”画上等号!!!
知识精讲
例13、如图,直线AD、BE被直线BF和AC所截,下列说法正确的是( )
A.∠3与∠4是同旁内角 B.∠2与∠5是同位角
C.∠6与∠1是内错角 D.∠2与∠6是同旁内角
D
知识精讲
例14、如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
D
知识精讲
例15、如图,不能得出AB∥CD的是( )
A.∠1=∠2 B.∠A=∠CDE
C.∠3=∠4 D.∠C+∠ABC=180°
【平行线的判定】
【分析】
选项C,∠1=∠2,根据“内错角相等,两直线平行”可得AD∥BC
C
知识精讲
例16、如图,下列条件中,能判断AD∥BE的是( )
A.∠1=∠2
B.∠3=∠4
C.∠B=∠DCE
D.∠B+∠BAD=180°
【分析】
选项C,∠B=∠DCE,根据“同位角相等,两直线平行”可得AB∥CD
D
知识精讲
例17、已知:如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°,求证:AB∥CD.
证明:∵DE平分∠BDC(已知),
∴∠BDC=2∠1(角平分线的定义).
∵BE平分∠ABD(已知),
∴∠ABD=2∠2(角平分线的定义),
∴∠BDC+∠ABD=2∠1+2∠2=2(∠1+∠2)(等式的性质);
∵∠1+∠2=90°(已知),
∴∠ABD+∠BDC=180°(等量代换),
∴AB∥CD(同旁内角互补,两直线平行).
课后总结
【三线八角】
定义:直线a、b与c相交(两条直线a、b被第三条直线c所截)构成八个角
【同位角】
定义:在被截线同侧,且在截线同侧的两个角。一个三线八角模型中有4对同位角
【内错角】
定义:在被截线内侧,且在截线两侧的两个角。一个三线八角模型中有2对内错角
【同旁内角】
定义:在被截线内侧,且在截线同侧的两个角。一个三线八角模型中有2对同旁内角
1
2
F型
Z型
3
6
U型
1
6
【平行线的判定方法】
一、同位角相等,两直线平行。二、内错角相等,两直线平行。三、同旁内角互补,两直线平行。
谢谢学习
Thank you for learning
探索直线平行的条件
Explore the condition for parallel lines
苏科版七年级下册第7章平面图形的认识(二)
教学目标
01
认识三线八角模型,并借助于三线八角模型理解同位角、内错角与同旁内角
02
区分同位角、内错角与同旁内角,并能根据对应的模型快速识别出这三类角
03
理解平行线的三种判定方法,并将其熟练应用于平行线的判断与证明当中去
三线八角与同位角
知识精讲
复习引入
01
平行
猴子最讨厌什么呢?
知识精讲
复习引入
01
Q1:什么是平行线?
在同一平面内,不相交的两条直线叫做平行线
如图,两条直线互相平行,记作a∥b或AB∥CD
C
a
b
D
A
B
知识精讲
复习引入
01
Q2:如何用直尺和三角尺画平行线?
放
移
画
a
a
b
画
a
知识精讲
问题引入
01
Q3:如图,∠1与∠2之间有怎样的数量关系?与直线a、b平行有何关联?
a
b
2
1
∠1=∠2(∠1与∠2对应着同一把三角尺的同一个角)
∵∠1=∠2,∴a∥b
a
b
2
1
1
a
b
2
知识精讲
问题引入
01
Q4:如图,∠1与∠2不相等,直线a、b平行吗?
a
b
c
2
1
不平行
∠1与∠2是否相等,决定了直线a、b是否平行
Q5:这么重要的∠1与∠2有什么特别的名字呢?
像∠1与∠2这样的一对角称为同位角
知识精讲
问题引入
01
Q6:两条直线a、b被第三条直线c所截成的角共有几个?
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
8个
被截直线
被截直线
截
线
同位角在被截线同侧
在截线同侧
问题引入
01
Q7:同位角与被截线、截线之间有何位置关系?
知识精讲
问题引入
01
Q8:同位角有几对?
4对
∠1与∠2
∠3与∠4
∠5与∠6
∠7与∠8
1
2
F型
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
02
知识精讲
【三线八角】
定义:直线a、b与c相交(两条直线a、b被第三条直线c所截)构成八个角
三线八角
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
02
知识精讲
【同位角】
定义:在被截线同侧,且在截线同侧的两个角
一个三线八角模型中有4对同位角
同位角
1
2
F型
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
02
知识精讲
平行线的判定(一)
【平行线的判定(一)】
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
简记:同位角相等,两直线平行
a
b
2
1
c
【符号语言】
∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
知识精讲
例1、如图,∠A的同位角是( )
A.∠BOE B.∠AOE C.∠BOD D.∠AOD
【同位角】
A
知识精讲
例2、若∠1与∠2的关系是同位角,∠1=30°,则∠2=( )
A.30° B.150° C.50°或130° D.不确定
D
【分析】
不要把“同位角”与“相等”画上等号!!!
知识精讲
例3、下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
C
知识精讲
例4、如图,下列图形中的∠1和∠2不是同位角的是( )
A. B.
C. D.
C
知识精讲
例5、如图,已知AB⊥BC,∠1+∠2=90°,∠2=∠3.求证:BE∥DF.
【平行线的判定】
证明:
∵AB⊥BC(已知),
∴∠ABC=90°(垂直的定义),
即∠3+∠4=90°(等量代换).
∵∠1+∠2=90°,且∠2=∠3(已知),
∴∠1+∠3=90°(等量代换),
∴∠1=∠4(等量代换),
∴BE∥DF(同位角相等,两直线平行).
内错角
Q1:如图,直线a、b被直线c所截,∠1=∠3,直线a与直线b平行吗?
a
b
2
1
c
3
只要说明同位角∠1、∠2相等,就可以知道a∥b了
∵∠2与∠3是对顶角(已知)
∴∠2=∠3(对顶角相等)
又∵∠1=∠3(已知)
∴∠1=∠2(等量代换)
∴a∥b(同位角相等,两直线平行)
∠2与∠3是对顶角,∠1=∠3
【总结】
∵∠1=∠3,……,∴a∥b
问题引入
01
知识精讲
问题引入
01
Q2:如图,∠1与∠3不相等,直线a、b平行吗?
不平行
∠1与∠3是否相等,决定了直线a、b是否平行
Q3:这么重要的∠1与∠3又有什么特别的名字呢?
像∠1与∠3这样的一对角称为内错角
a
b
1
c
3
内错角在被截线内侧
在截线两侧
问题引入
01
Q4:内错角与被截线、截线之间有何位置关系?
被截直线
被截直线
截
线
知识精讲
问题引入
01
Q5:一个三线八角模型中,内错角有几对?
2对
∠1与∠8
∠3与∠6
Z型
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
3
6
02
知识精讲
【内错角】
定义:在被截线内侧,且在截线两侧的两个角
一个三线八角模型中有2对内错角
内错角
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
Z型
3
6
02
知识精讲
平行线的判定(二)
【平行线的判定(二)】
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
简记:内错角相等,两直线平行
a
b
1
c
3
【符号语言】
∵∠1=∠3(已知)
∴a∥b(内错角相等,两直线平行)
知识精讲
例6、已知∠1与∠2是内错角,则( )
A.∠1=∠2 B.∠1+∠2=180°
C.∠1<∠2 D.以上都有可能
D
【内错角】
【分析】
不要把“内错角”与“相等”画上等号!!!
知识精讲
例7、如图,在∠1、∠2、∠3、∠4、∠5、∠6中,内错角有( )
A.1对 B.2对 C.3对 D.4对
C
【分析】
∵直线DC、直线DG被直线AB所截,
∴∠1和∠5是内错角,∠3和∠6是内错角;
∵直线AB、直线AC被直线DG所截,
∴∠2和∠4是内错角.
知识精讲
例8、如图,下列判断正确的是( )
A.∠5与∠3是内错角 B.∠2与∠4是同位角
C.∠3与∠6是同位角 D.∠2与∠5是对顶角
D
知识精讲
例9、如图,下列条件中可以判定DE∥AB的是( )
A.∠E=∠DCA B.∠E=∠DCE C.∠E=∠CDE D.∠E=∠BCE
D
【平行线的判定】
知识精讲
例10、下列图形中,由∠1=∠2,能得到AB∥CD的是( )
A. B.
C. D.
【分析】
选项C,∠1=∠2,根据“内错角相等,两直线平行”可得AC∥BD
A
知识精讲
例11、如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,证明AE∥GF.
证明:∵∠BAG+∠AGD=180°(已知),
∠AGC+∠AGD=180°(邻补角的定义),
∴∠BAG=∠AGC(同角的补角相等).
∵EA平分∠BAG,
∴∠1=∠BAG(角平分线的定义).
∵FG平分∠AGC,
∴∠2=∠AGC,
∴∠1=∠2(等量代换),
∴AE∥GF(内错角相等,两直线平行).
同旁内角
Q1:如图,直线a、b被直线c所截,∠1+∠4=180°,直线a与直线b平行吗?
a
b
2
1
c
4
∠1、∠2都是∠4的补角
∵∠1+∠4=180°(已知)
且∠2+∠4=180°(邻补角的定义)
∴∠1=∠2(等量代换)
∴a∥b(同位角相等,两直线平行)
【总结】
∵∠1+∠4=180°,……,∴a∥b
问题引入
01
知识精讲
问题引入
01
Q2:如图,∠1+∠4≠180°,直线a、b平行吗?
不平行
∠1+∠4是否为180°,决定了直线a、b是否平行
Q3:这么重要的∠1与∠4又有什么特别的名字呢?
像∠1与∠4这样的一对角称为同旁内角
a
b
1
c
4
同旁内角在被截线内侧
在截线同侧
问题引入
01
Q4:同旁内角与被截线、截线之间有何位置关系?
被截直线
被截直线
截
线
知识精讲
问题引入
01
Q5:一个三线八角模型中,同旁内角有几对?
2对
∠1与∠6
∠3与∠8
U型
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
1
6
02
知识精讲
【同旁内角】
定义:在被截线内侧,且在截线同侧的两个角
一个三线八角模型中有2对同旁内角
同旁内角
5
7
3
1
b
8
4
6
2
a
c
被截线
被截线
截线
U型
1
6
02
知识精讲
平行线的判定(三)
【平行线的判定(三)】
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
简记:同旁内角互补,两直线平行
a
b
1
c
4
【符号语言】
∵∠1+∠4=180°(已知)
∴a∥b(同旁内角互补,两直线平行)
02
知识精讲
平行线的判定方法
【平行线的判定方法】
一、同位角相等,两直线平行。
二、内错角相等,两直线平行。
三、同旁内角互补,两直线平行。
知识精讲
例12、若∠1与∠2是同旁内角,则( )
A.∠1与∠2不可能相等 B.∠1与∠2一定互补
C.∠1与∠2可能互余 D.∠1与∠2一定相等
C
【同旁内角】
【分析】
不要把“同旁内角”与“互补”画上等号!!!
知识精讲
例13、如图,直线AD、BE被直线BF和AC所截,下列说法正确的是( )
A.∠3与∠4是同旁内角 B.∠2与∠5是同位角
C.∠6与∠1是内错角 D.∠2与∠6是同旁内角
D
知识精讲
例14、如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
D
知识精讲
例15、如图,不能得出AB∥CD的是( )
A.∠1=∠2 B.∠A=∠CDE
C.∠3=∠4 D.∠C+∠ABC=180°
【平行线的判定】
【分析】
选项C,∠1=∠2,根据“内错角相等,两直线平行”可得AD∥BC
C
知识精讲
例16、如图,下列条件中,能判断AD∥BE的是( )
A.∠1=∠2
B.∠3=∠4
C.∠B=∠DCE
D.∠B+∠BAD=180°
【分析】
选项C,∠B=∠DCE,根据“同位角相等,两直线平行”可得AB∥CD
D
知识精讲
例17、已知:如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°,求证:AB∥CD.
证明:∵DE平分∠BDC(已知),
∴∠BDC=2∠1(角平分线的定义).
∵BE平分∠ABD(已知),
∴∠ABD=2∠2(角平分线的定义),
∴∠BDC+∠ABD=2∠1+2∠2=2(∠1+∠2)(等式的性质);
∵∠1+∠2=90°(已知),
∴∠ABD+∠BDC=180°(等量代换),
∴AB∥CD(同旁内角互补,两直线平行).
课后总结
【三线八角】
定义:直线a、b与c相交(两条直线a、b被第三条直线c所截)构成八个角
【同位角】
定义:在被截线同侧,且在截线同侧的两个角。一个三线八角模型中有4对同位角
【内错角】
定义:在被截线内侧,且在截线两侧的两个角。一个三线八角模型中有2对内错角
【同旁内角】
定义:在被截线内侧,且在截线同侧的两个角。一个三线八角模型中有2对同旁内角
1
2
F型
Z型
3
6
U型
1
6
【平行线的判定方法】
一、同位角相等,两直线平行。二、内错角相等,两直线平行。三、同旁内角互补,两直线平行。
谢谢学习
Thank you for learning
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
