圆锥曲线 [上下学期通用]
图片预览








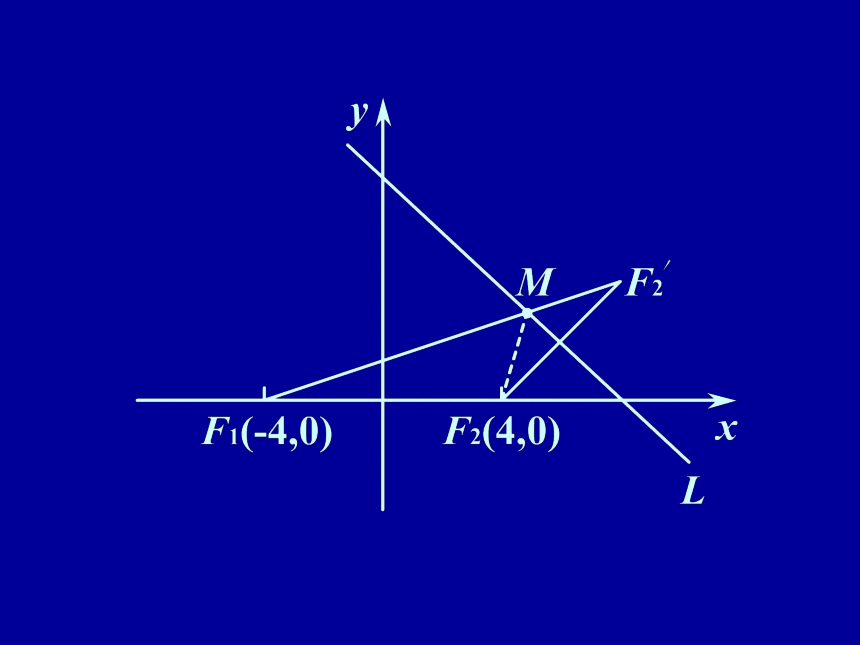

文档简介
课件47张PPT。圆锥曲线董世奎 圆锥曲线中的椭圆、双曲线、抛物线是平面解析几何的重点内容,本讲主要围绕下面三个问题加以讲解:
(1)理解并掌握椭圆、双曲线、抛物线的定义、方程及性质;
(2)掌握确定曲线方程的基本方法;
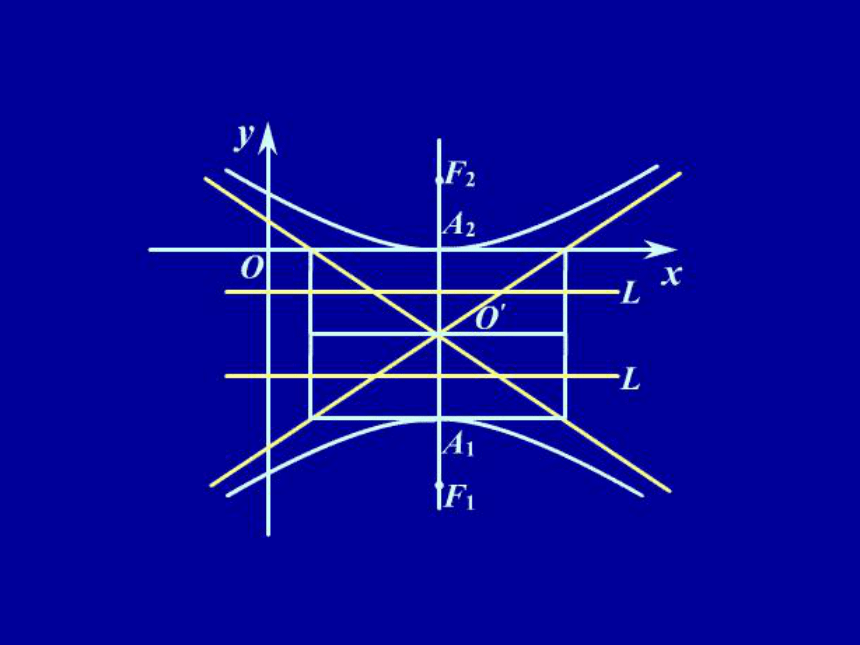
(3)初步了解曲线方程的应用. 例1 双曲线4x2-9y2-32x-36y+64=0的标准方程是___________,中心坐标O′( _______ ),实轴长___________,虚轴长_________,焦距_______,顶点坐标________,焦点坐标______,准线方程_____________,渐近线方程______,准线间距离_________,焦准距____________. 评析与引申
(1)求有心二次曲线与坐标系有关的性质的方法是:一求中心,二求出基
本量a,b,c, ,再以中心为准左右或上下移动即可求出,对于抛物线则以
顶点为准;
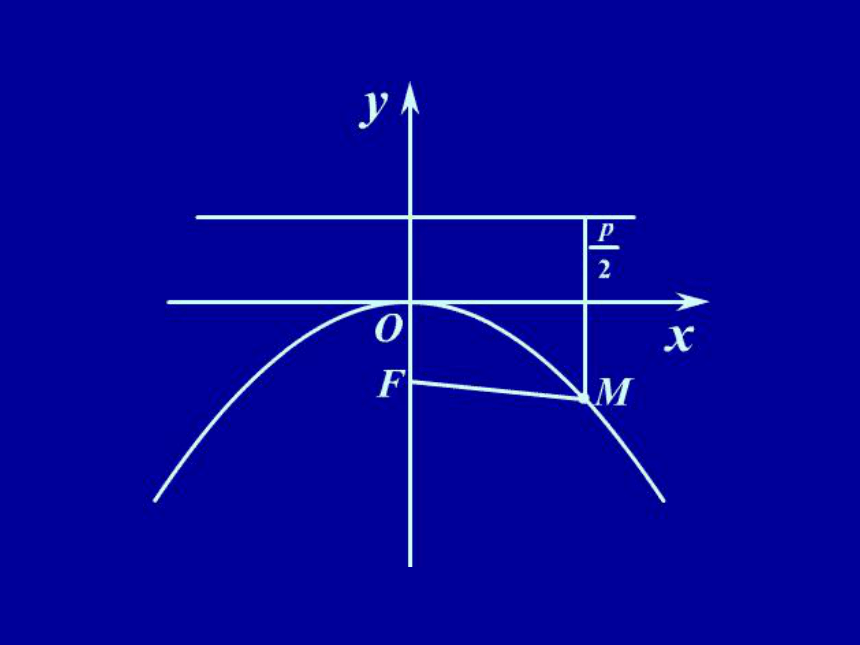
(2)求双曲线的渐近线方程,只需将方程中的常数项改为零分解因式即可. 例2 已知抛物线的顶点为坐标原点,焦点在y 轴上,抛物线上的点M(m, -2)到焦点的距离为4,则m等于 ( )
(A)4 (B)-2
(C)4或-4 (D)2或-2 分析 由已知可知抛物线如图所示,设所求抛物线方程为 x2 =-2py (p>0) .由已知和抛物线定义可得 .所求抛物线方程为:x2=-8y,将(m, -2) 代入上式m2=16?m=±4,应选(C). 例3 在直线L:x+y-8=0上任
取一点M,以双曲线 的焦点为焦点,过M作椭圆,问当M点在何处时所作椭圆的长轴最短,此时椭
圆方程是什么?
分析 由已知得F1(-4, 0), F2(4, 0) . 由图,原命题?在L上求一点M,使|F1M|+|F2M| 最小. 例4 求中心在原点,对称轴在坐标轴上,且过 的椭圆方程.
解:因为很难判断焦点在哪个坐标轴上,所以用一般式较好.可设所求椭圆方程为:
Ax2+Cy2=F(A,C,F同号) 例5 设双曲线
(0 < a < b)的半焦距为c,直线L过点(a,0)和(0,b),已知原点到直线 L 的距离为 ,则双曲线的离心率为 ( )
(A)2 (B)
(C) (D) 解: 如图,在Rt△AOB中,|OA|=a,|OB|=b, |AB| =c,由面积公式得: 例6 已知两点 给出下列曲线方程.
①4x+2y-1= 0;②x2+y2=3;
③ ;④ .在
曲线上存在点P,满足|MP|=|NP| 的所
有曲线方程是 ( )
(A)①③ (B)②④
(C)①②③ (D)②③④ 解:首先求出MN的垂直平分线方程是:2x+y+3=0,显然与①平行,从而排除了选项(A)和(C),由余下的(B),(D)可知只需判断2x+y+3=0与③的关系,前者代入后者得:∴△x=(24)2-4×9×16=0
∴2x+y+3=0与③有公共点,所以应选D. 评析与引申
本题既考查了直线与直线、直线与曲线的位置关系,更重要是考查了考生的分析问题的能力.当排除(A)、(C)后,根据(B)(D)的特点,找到问题的切入点是判断2x+y+3=0与③的位置关系. 例7 过抛物线 y=ax2 的焦点F 作直线 L 与抛物线交于A、B 两点,
记 | AF | =m,| BF |= n,则 等于 ( )
(A)4a (B)-4a
(C) (D) 分析 在题设中只给出了AB过焦点
,并没有限定倾角?,这就间
接告诉我们 与AB的倾角? 无关,
这就是变量数学中的不变性.可设?=0,
由抛物线的定义 .
∴ ,应选(A). 评析与引申
(1)注意到 ,其中m+n=|AB|表示弦AB的长,m·n=|AF|·|BF| 表示线段积,显然用极
坐标 和直线AB 的参数方程 ,也可以求出
.特别是用极坐标更简
捷,但这里更重要是考查学生的直觉
思维能力. (2)本题解法的逻辑依据是:
一般成立,特殊一定成立? 特殊不成立,一般一定不成立. 例8 如图,直线l1⊥l2于M点,点N?l1,以A、B为端点的曲线C上任意一点到l2的距离与到点N的距离
相等.若△AMN 为锐角三角形,
,且| BN |= 6,建立适当的坐标系,求曲线C 的方程. 分析 由已知,根据抛物线的定义,可知曲线C是以N为焦点,直线l2为准线的抛物线的一段,于是有
解: 以MN的中点O为原点,l1为x轴如图建立直角坐标系xoy.
由已知可设曲线C的方程为:
y2=2px (p>0,xA≤x≤xB,y>0)又∵解得: 或 ①②
∴ 因为△AMN为锐角三角形,所以
,故p=4,xA=1.
由B点在曲线C上,
.
综上:曲线C的方程为
y2=8x(1≤x≤4,y>0). 评析与引申
确定曲线方程基本方法之一就是布列关于未知量的方程(组),解之即可. 例9 正方形ABCD在直角坐标平面内,已知其中一条边AB在直线y=x+4上,C、D两点在抛物线x=y2上,求正方形面积. 分析 由图,不难发现,求ABCD的面积?求弦CD的长.若设CD方程为y=x+b,则|CD|=f(b).又AB与CD距离为g(b).由f(b)=g(b)可求出b,即可求出|CD|=f(b). 解:设CD方程为y=x+b,代入y2=x
x2+(2b-1)x+b2=0
∴ .
∴
又 例10 已知定点A(a,0)(a>0)
和定直线l :x=-1,B是直线l 上的动点,∠BOA 的平分线交AB于C 点,求C 点的轨迹方程,并讨论方程表示的曲线类型与a 的关系.
分析 这是两条动直线OC与AB的交点轨迹问题,其思路是引入变量,分别写出两条直线方程,消参数即可.αB解:当B点不在x轴上时,
设∠AOC=?,则∠AOB=2?,
则OC方程为y =x tan? ①
OB方程为y=x tan2?
∴B(-1,-tan2?)
AB方程为: ② 由① x≠0 ∴ 代入②得
(a-1)x2-(a+1)y2+2ax=0
(0<x<a) ③
当B点在x轴上时,C(0,0)显然在③上.综上C点的轨迹方程为
(a-1)x2-(a+1)y2+2ax=0 (0≤x<a)讨论:
(1)当a=1时,轨迹方程化为
y2=x(0≤x<1),此时,方程③表示抛物线弧段;
(2)当a≠1时,轨迹方程化为 所以,当0<a<1时,方程③表示椭圆弧段;
当a>1时,方程③表示双曲线一支的弧段.
(1)理解并掌握椭圆、双曲线、抛物线的定义、方程及性质;
(2)掌握确定曲线方程的基本方法;
(3)初步了解曲线方程的应用. 例1 双曲线4x2-9y2-32x-36y+64=0的标准方程是___________,中心坐标O′( _______ ),实轴长___________,虚轴长_________,焦距_______,顶点坐标________,焦点坐标______,准线方程_____________,渐近线方程______,准线间距离_________,焦准距____________. 评析与引申
(1)求有心二次曲线与坐标系有关的性质的方法是:一求中心,二求出基
本量a,b,c, ,再以中心为准左右或上下移动即可求出,对于抛物线则以
顶点为准;
(2)求双曲线的渐近线方程,只需将方程中的常数项改为零分解因式即可. 例2 已知抛物线的顶点为坐标原点,焦点在y 轴上,抛物线上的点M(m, -2)到焦点的距离为4,则m等于 ( )
(A)4 (B)-2
(C)4或-4 (D)2或-2 分析 由已知可知抛物线如图所示,设所求抛物线方程为 x2 =-2py (p>0) .由已知和抛物线定义可得 .所求抛物线方程为:x2=-8y,将(m, -2) 代入上式m2=16?m=±4,应选(C). 例3 在直线L:x+y-8=0上任
取一点M,以双曲线 的焦点为焦点,过M作椭圆,问当M点在何处时所作椭圆的长轴最短,此时椭
圆方程是什么?
分析 由已知得F1(-4, 0), F2(4, 0) . 由图,原命题?在L上求一点M,使|F1M|+|F2M| 最小. 例4 求中心在原点,对称轴在坐标轴上,且过 的椭圆方程.
解:因为很难判断焦点在哪个坐标轴上,所以用一般式较好.可设所求椭圆方程为:
Ax2+Cy2=F(A,C,F同号) 例5 设双曲线
(0 < a < b)的半焦距为c,直线L过点(a,0)和(0,b),已知原点到直线 L 的距离为 ,则双曲线的离心率为 ( )
(A)2 (B)
(C) (D) 解: 如图,在Rt△AOB中,|OA|=a,|OB|=b, |AB| =c,由面积公式得: 例6 已知两点 给出下列曲线方程.
①4x+2y-1= 0;②x2+y2=3;
③ ;④ .在
曲线上存在点P,满足|MP|=|NP| 的所
有曲线方程是 ( )
(A)①③ (B)②④
(C)①②③ (D)②③④ 解:首先求出MN的垂直平分线方程是:2x+y+3=0,显然与①平行,从而排除了选项(A)和(C),由余下的(B),(D)可知只需判断2x+y+3=0与③的关系,前者代入后者得:∴△x=(24)2-4×9×16=0
∴2x+y+3=0与③有公共点,所以应选D. 评析与引申
本题既考查了直线与直线、直线与曲线的位置关系,更重要是考查了考生的分析问题的能力.当排除(A)、(C)后,根据(B)(D)的特点,找到问题的切入点是判断2x+y+3=0与③的位置关系. 例7 过抛物线 y=ax2 的焦点F 作直线 L 与抛物线交于A、B 两点,
记 | AF | =m,| BF |= n,则 等于 ( )
(A)4a (B)-4a
(C) (D) 分析 在题设中只给出了AB过焦点
,并没有限定倾角?,这就间
接告诉我们 与AB的倾角? 无关,
这就是变量数学中的不变性.可设?=0,
由抛物线的定义 .
∴ ,应选(A). 评析与引申
(1)注意到 ,其中m+n=|AB|表示弦AB的长,m·n=|AF|·|BF| 表示线段积,显然用极
坐标 和直线AB 的参数方程 ,也可以求出
.特别是用极坐标更简
捷,但这里更重要是考查学生的直觉
思维能力. (2)本题解法的逻辑依据是:
一般成立,特殊一定成立? 特殊不成立,一般一定不成立. 例8 如图,直线l1⊥l2于M点,点N?l1,以A、B为端点的曲线C上任意一点到l2的距离与到点N的距离
相等.若△AMN 为锐角三角形,
,且| BN |= 6,建立适当的坐标系,求曲线C 的方程. 分析 由已知,根据抛物线的定义,可知曲线C是以N为焦点,直线l2为准线的抛物线的一段,于是有
解: 以MN的中点O为原点,l1为x轴如图建立直角坐标系xoy.
由已知可设曲线C的方程为:
y2=2px (p>0,xA≤x≤xB,y>0)又∵解得: 或 ①②
∴ 因为△AMN为锐角三角形,所以
,故p=4,xA=1.
由B点在曲线C上,
.
综上:曲线C的方程为
y2=8x(1≤x≤4,y>0). 评析与引申
确定曲线方程基本方法之一就是布列关于未知量的方程(组),解之即可. 例9 正方形ABCD在直角坐标平面内,已知其中一条边AB在直线y=x+4上,C、D两点在抛物线x=y2上,求正方形面积. 分析 由图,不难发现,求ABCD的面积?求弦CD的长.若设CD方程为y=x+b,则|CD|=f(b).又AB与CD距离为g(b).由f(b)=g(b)可求出b,即可求出|CD|=f(b). 解:设CD方程为y=x+b,代入y2=x
x2+(2b-1)x+b2=0
∴ .
∴
又 例10 已知定点A(a,0)(a>0)
和定直线l :x=-1,B是直线l 上的动点,∠BOA 的平分线交AB于C 点,求C 点的轨迹方程,并讨论方程表示的曲线类型与a 的关系.
分析 这是两条动直线OC与AB的交点轨迹问题,其思路是引入变量,分别写出两条直线方程,消参数即可.αB解:当B点不在x轴上时,
设∠AOC=?,则∠AOB=2?,
则OC方程为y =x tan? ①
OB方程为y=x tan2?
∴B(-1,-tan2?)
AB方程为: ② 由① x≠0 ∴ 代入②得
(a-1)x2-(a+1)y2+2ax=0
(0<x<a) ③
当B点在x轴上时,C(0,0)显然在③上.综上C点的轨迹方程为
(a-1)x2-(a+1)y2+2ax=0 (0≤x<a)讨论:
(1)当a=1时,轨迹方程化为
y2=x(0≤x<1),此时,方程③表示抛物线弧段;
(2)当a≠1时,轨迹方程化为 所以,当0<a<1时,方程③表示椭圆弧段;
当a>1时,方程③表示双曲线一支的弧段.
