2021-2022学年山东省青岛市城阳区九年级(上)期末数学试卷 含解析
文档属性
| 名称 | 2021-2022学年山东省青岛市城阳区九年级(上)期末数学试卷 含解析 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-27 00:00:00 | ||
图片预览

文档简介
2021-2022学年山东省青岛市城阳区九年级(上)期末数学试卷
一、单选题(本题满分24分,共8道小题,每小题3分)
1.(3分)方程x2=5x的解是( )
A.x=5 B.x=0 C.x1=﹣5;x2=0 D.x1=5;x2=0
2.(3分)将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的俯视图是( )
A. B. C. D.
3.(3分)如图,晚上小丽在路灯下散步,在小丽由A处走到B处的过程中,她在地上的影子( )
A.逐渐变长 B.逐渐变短
C.先变短后变长 D.先变长后变短
4.(3分)若点A(x1,﹣4),B(x2,2),C(x3,4)都在反比例函数y=的图象上,则x1、x2、x3的大小关系式( )
A.x1<x2<x3 B.x2<x3<x1 C.x3<x1<x2 D.x1<x3<x2
5.(3分)随着新冠疫苗的全民接种,疫苗需求仍存在较大缺口,某制药公司引进一条新冠疫苗生产线,开工第一天生产疫苗8000盒,第三天生产疫苗9680盒,若每天的增长率相同,求每天的增长率是多少?设每天的增长率是x,则可列方程为( )
A.8000x=9680
B.8000(1+x)=9680
C.8000(1+x)2=9680
D.8000+8000(1+x)+8000(1+x)2=9680
6.(3分)如图,在Rt△ABC中,∠C=90°,AB=5,cosA=,则tanB=( )
A. B. C. D.无法确定
7.(3分)如图,在正方形ABCD中,AB=9,点E、F分别在边AB、CD上,∠FEB=120°.若将四边形EBCF沿EF折叠,点C恰好落在AD边C'上,则C'D的长度为( )
A.3 B.3 C.3 D.
8.(3分)如图是二次函数y=ax2+bx的大致图象,则一次函数y=(a+b)x﹣b的图象大致是( )
A. B.
C. D.
二、填空题(本题满分24分,共8道小题,每小题3分)
9.(3分)计算:sin30°+tan30°= .
10.(3分)在一个不透明的口袋中装有6个黄球和n个白球,它们除颜色外完全相同,若从中随机摸出一球,摸到黄球的概率为,则n的值是 .
11.(3分)如图,在一块长32m、宽24米的矩形荒地上,要建造一个矩形花园,图中阴影部分是花园,并使花园所占面积为荒地面积的一半,花园外部四周修建宽度相同的小路,求图中的小路的宽是多少米?设小路的宽度为xm,所列方程式是 .
12.(3分)若二次函数y=﹣x2+4x﹣2m的图象与x轴没有交点,则m的取值范围是 .
13.(3分)如图,在菱形ABCD中,AB=12,∠BCD=60°,E是AD中点,BE交AC于点F,连接DF,则DF的长为 .
14.(3分)如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(﹣2,4),将△AOB绕点A顺时针旋转90°得到△ADC,点B的对应点C恰好落在反比例函数y=上,则k的值为 .
15.(3分)如图,四边形ABCD是矩形,点E在线段AD的延长线上,连接BE交CD于点F,∠BEC=2∠AEB,点G是BF的中点,若DE=1,BF=10,则AB的长为 .
16.(3分)如图1,是一座抛物线型拱桥侧面示意图,水面宽AB与桥长CD均为12m,在距离D点3m的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.如图2,桥面上方有3根高度均为5m的支柱CG、OH、DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为2m,下面结论正确的是 (填写正确结论序号).
①图1抛物线型拱桥的函数表达式y=﹣x2.
②图2右边钢缆抛物线的函数表达式y=2+2.
③图2左边钢缆抛物线的函数表达式y=2+2.
④图2在钢缆和桥拱之间竖直装饰若干条彩带,彩带长度的最小值是3m.
三、作图题(本题满分4分)用圆规、直尺作图,不写做法,但要保留作图痕迹
17.(4分)已知:△ABC中,E是AB上一点,求作:矩形EFGH,使FG在BC边上,H在AC边上.
四、解答题(本题共有8道小题,满分68分)
18.(10分)计算:
(1)2x2﹣4x+=0(配方法);
(2)3(x﹣2)2=x2﹣4(用适当方法).
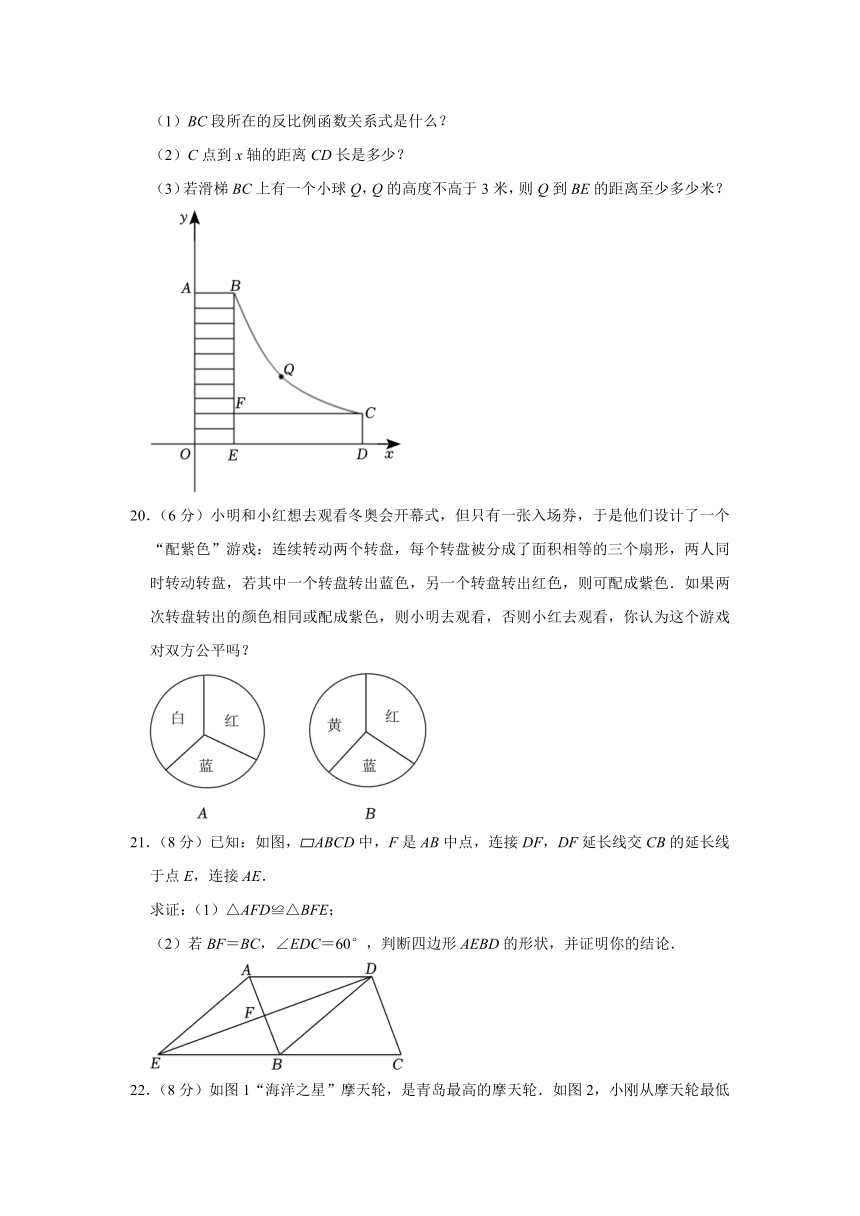
19.(6分)如图是海洋公园娱乐设施“水上滑梯”的侧面图,建立如图坐标系.其中BC段可看成是反比例函数图象的一段,矩形AOEB为向上攀爬的梯子,梯子高6米,宽1米,出口C点到BE的距离CF为11米,求:
(1)BC段所在的反比例函数关系式是什么?
(2)C点到x轴的距离CD长是多少?
(3)若滑梯BC上有一个小球Q,Q的高度不高于3米,则Q到BE的距离至少多少米?
20.(6分)小明和小红想去观看冬奥会开幕式,但只有一张入场券,于是他们设计了一个“配紫色”游戏:连续转动两个转盘,每个转盘被分成了面积相等的三个扇形,两人同时转动转盘,若其中一个转盘转出蓝色,另一个转盘转出红色,则可配成紫色.如果两次转盘转出的颜色相同或配成紫色,则小明去观看,否则小红去观看,你认为这个游戏对双方公平吗?
21.(8分)已知:如图, ABCD中,F是AB中点,连接DF,DF延长线交CB的延长线于点E,连接AE.
求证:(1)△AFD≌△BFE;
(2)若BF=BC,∠EDC=60°,判断四边形AEBD的形状,并证明你的结论.
22.(8分)如图1“海洋之星”摩天轮,是青岛最高的摩天轮.如图2,小刚从摩天轮最低处B出发沿水平方向向右行走15米到达C,再经过一段坡度为i=3:4,坡长为5米的斜坡CD到达点D,然后再沿水平方向向右行走一段时间后到达点E.在E处有一垂直地面的平台EF,测得EF=12米,在点F处,测得点D的俯角为52°,摩天轮最高处A的仰角为21°.AB所在的直线垂直于地面,垂足为O,点A、B、C、D、E、F、O在同一平面内,求AO的长度约为多少米?(结果精确到1米,参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.3,sin21°≈0.36,cos21°≈0.93,tan21°≈0.4)
23.(10分)某公司销售一种商品,成本为4元/件,公司规定售价不能低于6元/件,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的几组对应数值如表:
销售单价x(元) 8 9 10 11 12
日销售量y(件) 80 75 70 65 60
(1)求出y与x之间的函数关系式;
(2)该商品的销售单价定为多少元,公司日销售此商品获得的利润最大?最大利润是多少元?
(3)若该商品的日销售量不少于70件,公司日销售此商品获得的最大利润是多少元?
24.(10分)探究一:在平面直角坐标系中探究的几何意义
例如:已知A(1,4),B(﹣4,﹣2),如果要求A、B两点之间的距离,可以构造如图1所示的直角三角形,则A、B之间的距离为 .
结论:在平面直角坐标系中,已知平面内A(x1,y1)、B(x2,y2)两点坐标,则A、B两点之间的距离等于因此,的几何意义可以理解为点A(x,y)与点B(a,b)之间的距离AB.
应用一:+的几何意义可以理解为点A(x,y)与点E( , )的距离和点A(x,y)与点F( , )的距离之和.
探究二:求代数式+的最小值.
解:+=+
如图2,建立平面直角坐标系,点P(x,0)是x轴上一点,则可以看成P(x,0)与点A( , )的距离.可以看成点P(x,0)与点B( , )的距离.
所以原代数式的值可以看成线段PA与PB的长度之和,PA+PB的最小值就是原代数式的最小值,设点A关于x轴的对称点为A',则PA=PA',因此求PA+PB的最小值,只需求PA'+PB的最小值.而点A'、B之间的所有连线中线段最短,所以PA'+PB的最小值为线段A'B的长度.为此,构造直角三角形A'CB,所以A'B= .
即+的最小值为 .
拓展:代数式+的最小值为 .
25.(10分)已知:如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=9cm,BC=25cm,CD=12cm,连接AC,点E从点B出发沿BC方向匀速运动,速度为4cm/s;同时,点F从点C出发沿CA方向匀速运动,速度为3cm/s.过点E作EG⊥AB交AB于点G,连接EF,当一点停止运动时,另一点也停止运动,设运动时间为t(s)(0<t<4).
(1)当点F在线段EC的垂直平分线上时,求t的值;
(2)当四边形AGEF是矩形时,求t的值;
(3)设四边形AGEF的面积为S(cm2),求S与t的函数关系式;
(4)取CD的中点Q,是否存在某一时刻t,使得点E、F、Q在同一条直线上?若存在,请求出t的值;若不存在,请说明理由.
2021-2022学年山东省青岛市城阳区九年级(上)期末数学试卷
参考答案与试题解析
一、单选题(本题满分24分,共8道小题,每小题3分)
1.(3分)方程x2=5x的解是( )
A.x=5 B.x=0 C.x1=﹣5;x2=0 D.x1=5;x2=0
【分析】先把方程化为一般式,然后利用因式分解法解方程.
【解答】解:x2﹣5x=0,
x(x﹣5)=0,
x=0或x﹣5=0,
所以x1=0,x2=5,
故选:D.
2.(3分)将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的俯视图是( )
A. B. C. D.
【分析】根据俯视图的画法画出它的俯视图即可.
【解答】解:这个几何体的俯视图为:
故选:C.
3.(3分)如图,晚上小丽在路灯下散步,在小丽由A处走到B处的过程中,她在地上的影子( )
A.逐渐变长 B.逐渐变短
C.先变短后变长 D.先变长后变短
【分析】小亮由A处径直路灯下,他得影子由长变短,再从路灯下到B处,他的影子则由短变长.
【解答】解:在小亮从A点走向B点的过程中,他在地上的影子先变短后变长.
故选:C.
4.(3分)若点A(x1,﹣4),B(x2,2),C(x3,4)都在反比例函数y=的图象上,则x1、x2、x3的大小关系式( )
A.x1<x2<x3 B.x2<x3<x1 C.x3<x1<x2 D.x1<x3<x2
【分析】解法一:直接将点A、B、C的坐标代入反比例函数y=中,求出x1、x2、x3,再比较大小即可.
解法二:根据反比例函数的图象和性质,结合点A、B、C纵坐标的数值,即可解答.
【解答】解法一:解:在反比例函数y=中,
当y=﹣4时,x1=﹣2,
当y=2时,x2=4,
当y=4时,x3=2,
∴x1<x3<x2.
故选:D.
解法二:解:在反比例函数y=中,k=8>0,
∴函数图象在一、三象限,在每个象限内,y随x的增大而减小,
∵点B、C在第一象限,且2<4,
∴x2>x3>0,
∵点A在第三象限,
∴x1<0,
∴x1<x3<x2,
故选:D.
5.(3分)随着新冠疫苗的全民接种,疫苗需求仍存在较大缺口,某制药公司引进一条新冠疫苗生产线,开工第一天生产疫苗8000盒,第三天生产疫苗9680盒,若每天的增长率相同,求每天的增长率是多少?设每天的增长率是x,则可列方程为( )
A.8000x=9680
B.8000(1+x)=9680
C.8000(1+x)2=9680
D.8000+8000(1+x)+8000(1+x)2=9680
【分析】利用第三天生产疫苗的数量=第一天生产疫苗的数量×(1+每天的增长率)2,即可得出关于x的一元二次方程,此题得解.
【解答】解:根据题意得8000(1+x)2=9680,
故选:C.
6.(3分)如图,在Rt△ABC中,∠C=90°,AB=5,cosA=,则tanB=( )
A. B. C. D.无法确定
【分析】根据锐角三角函数的定义求出AC,再根据勾股定理求出BC,由锐角三角函数的定义可得答案.
【解答】解:在Rt△ABC中,∠C=90°,
∵AB=5,cosA==,
∴AC=4,
∴BC==3,
∴tanB==,
故选:A.
7.(3分)如图,在正方形ABCD中,AB=9,点E、F分别在边AB、CD上,∠FEB=120°.若将四边形EBCF沿EF折叠,点C恰好落在AD边C'上,则C'D的长度为( )
A.3 B.3 C.3 D.
【分析】根据翻折的性质和正方形及勾股定理的有关性质求解.
【解答】解:在正方形ABCD中,CD=AB=9,CD∥AB,∠D=90°,
∴∠FEB+∠EFC=180°,
∴∠EFC=∠C′FE=60°,
∴∠C′FD=180°﹣∠EFC﹣∠C′FE=60°,
∴∠DC′F=30°,
∴C′F=2DF,
又∵C′F=CF,CF+DF=9,
∴DF=3,C′F=6,
∴C′D==3,
故选:B.
8.(3分)如图是二次函数y=ax2+bx的大致图象,则一次函数y=(a+b)x﹣b的图象大致是( )
A. B.
C. D.
【分析】根据二次函数的图象可以判断a、b、﹣b、a+b的正负情况,从而可以得到一次函数经过哪几个象限,本题得以解决.
【解答】解:由二次函数的图象可知,
a<0,b<0,
∴a+b<0,﹣b>0,
∴一次函数y=(a+b)x﹣b的图象在第一、二、四象限,
故选:B.
二、填空题(本题满分24分,共8道小题,每小题3分)
9.(3分)计算:sin30°+tan30°= 1 .
【分析】直接利用特殊角的三角函数值代入,进而计算得出答案.
【解答】解:原式=+×
=+
=1.
故答案为:1.
10.(3分)在一个不透明的口袋中装有6个黄球和n个白球,它们除颜色外完全相同,若从中随机摸出一球,摸到黄球的概率为,则n的值是 18 .
【分析】根据口袋中装有6个黄球和n个白球,故球的总个数为(6+n),再根据黄球的概率公式列式解答即可.
【解答】解:根据题意得:=,
解得n=18.
经检验,n=18是原分式方程的解.
故答案为:18.
11.(3分)如图,在一块长32m、宽24米的矩形荒地上,要建造一个矩形花园,图中阴影部分是花园,并使花园所占面积为荒地面积的一半,花园外部四周修建宽度相同的小路,求图中的小路的宽是多少米?设小路的宽度为xm,所列方程式是 (32﹣2x)(24﹣2x)=×32×24 .
【分析】根据小路的宽度,可得出矩形花园的长为(32﹣2x)m,宽为(24﹣2x)m,结合矩形花园所占面积为荒地面积的一半,即可得出关于x的一元二次方程,此题得解.
【解答】解:∵小路的宽度为xm,
∴矩形花园的长为(32﹣2x)m,宽为(24﹣2x)m.
根据题意得:(32﹣2x)(24﹣2x)=×32×24,
故答案为:(32﹣2x)(24﹣2x)=×32×24.
12.(3分)若二次函数y=﹣x2+4x﹣2m的图象与x轴没有交点,则m的取值范围是 m>2 .
【分析】利用判别式的意义得到Δ=42﹣4×(﹣1)×(﹣2m)<0,然后解不等式即可.
【解答】解:∵二次函数y=﹣x2+4x﹣2m的图象与x轴没有交点,
∴Δ=42﹣4×(﹣1)×(﹣2m)<0,
解得m>2.
故答案为:m>2.
13.(3分)如图,在菱形ABCD中,AB=12,∠BCD=60°,E是AD中点,BE交AC于点F,连接DF,则DF的长为 4 .
【分析】连接BD,则△ABD为等边三角形,点F为△ABD的外心,利用等边三角形的性质,可得出BE的长,由∠EDF=30°,可得出DF=2EF,进而可求出DF的长.
【解答】解:连接BD,则△ABD为等边三角形,点F为△ABD的外心,如图所示.
∵E是AD中点,AB=12,
∴BE⊥AD,AE=AB=×12=6,
∴BE===6.
又∵∠EDF=×60°=30°,
∴DF=2EF,
∴DF=BF=BE=×6=4.
故答案为:4.
14.(3分)如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(﹣2,4),将△AOB绕点A顺时针旋转90°得到△ADC,点B的对应点C恰好落在反比例函数y=上,则k的值为 ﹣24 .
【分析】根据题意和旋转的性质,可以得到点C的坐标,由点C恰好落在反比例函数y=上,从而可以得到k的值,本题得以解决.
【解答】解:∵OB在x轴上,∠ABO=90°,点A的坐标为(﹣2,4),将△AOB绕点A顺时针旋转90°得到△ADC,∴点C的坐标为(﹣6,4),
∵点B的对应点C恰好落在反比例函数y=上,
∴4=,
解得,k=﹣24,
故答案为:﹣24.
15.(3分)如图,四边形ABCD是矩形,点E在线段AD的延长线上,连接BE交CD于点F,∠BEC=2∠AEB,点G是BF的中点,若DE=1,BF=10,则AB的长为 2 .
【分析】根据直角三角形斜边上的中线等于斜边的一半可得BG=FG=GC=BF=5,然后根据等边对等角的性质可得∠GBC=∠GCB,再结合两直线平行,内错角相等可得∠GBC=∠AEB,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CGE=2∠AEB,从而得到∠BEC=∠CGE,再利用等角对等边的性质得到CE=CG,然后利用勾股定理列式计算即可得解.
【解答】解:∵四边形ABCD是矩形,
∴∠BCF=90°,
∵点G是BF的中点,
∴BG=FG=GC=BF=5,
∴∠GBC=∠GCB,
∵AD∥BC,
∴∠GBC=∠AEB,
∴∠CGE=∠GBC+∠GCB=2∠GBC=2∠AEB,
∵∠BEC=2∠AEB,
∴∠BEC=∠CGE,
∴CE=CG=5,
在Rt△CDE中,DE=1,
∴CD===2.
∴AB=CD=2.
故答案为:2.
16.(3分)如图1,是一座抛物线型拱桥侧面示意图,水面宽AB与桥长CD均为12m,在距离D点3m的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.如图2,桥面上方有3根高度均为5m的支柱CG、OH、DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为2m,下面结论正确的是 ①②③④ (填写正确结论序号).
①图1抛物线型拱桥的函数表达式y=﹣x2.
②图2右边钢缆抛物线的函数表达式y=2+2.
③图2左边钢缆抛物线的函数表达式y=2+2.
④图2在钢缆和桥拱之间竖直装饰若干条彩带,彩带长度的最小值是3m.
【分析】①利用待定系数法求函数解析式,然后结合二次函数图象上点的坐标特征计算求解;
②由图象分析右边钢缆所在抛物线的顶点坐标为(3,2),然后利用待定系数法求函数解析式;
③用与②相同的方法即可求出函数解析式;
④彩带的长度为Lm,利用L(x﹣3)2+2﹣(﹣x2)=(x﹣2)2+3,由函数的性质即可得出结论.
【解答】解:根据题意可知点F的坐标为(3,﹣1.5),
可设拱桥侧面所在二次函数表达式为:y1=a1x2,
将F(3,﹣1.5)代入y1=a1x2有:﹣1.5=9a1,
解得a1=﹣,
∴y1=﹣x2,
故①正确;
由题意可知右边钢缆所在抛物线的顶点坐标为(3,2),可设其表达式为y=a2(x﹣3)2+2,
将H(0,5)代入其表达式有:5=a2(0﹣3)2+2,
解得a2=,
∴右边钢缆所在抛物线表达式为:y=(x﹣3)2+2,
故②正确;
同理可知,③正确;
设彩带的长度为Lm,
则L=(x﹣3)2+2﹣(﹣x2)=x2﹣2x+5+x2=x2﹣2x+5=(x﹣2)2+3.
∵>0,
∴当x=2时,L最小,最小值为3.
故④正确.
故答案为:①②③④.
三、作图题(本题满分4分)用圆规、直尺作图,不写做法,但要保留作图痕迹
17.(4分)已知:△ABC中,E是AB上一点,求作:矩形EFGH,使FG在BC边上,H在AC边上.
【分析】根据要求作出图形即可.
【解答】解:如图,矩形EFGH即为所求.
四、解答题(本题共有8道小题,满分68分)
18.(10分)计算:
(1)2x2﹣4x+=0(配方法);
(2)3(x﹣2)2=x2﹣4(用适当方法).
【分析】(1)利用配方法得到(x﹣1)2=,然后利用直接开平方法解方程;
(2)先把方程化为3(x﹣2)2﹣(x+2)(x﹣2)=0,再利用因式分解法把方程转化为x﹣2=0或3x﹣6﹣x﹣2=0,然后解两个一次方程即可.
【解答】解:(1)2x2﹣4x+=0,
2x2﹣4x=﹣,
x2﹣2x=﹣,
x2﹣2x+1=﹣+1,
(x﹣1)2=,
x﹣1=±,
所以x1=1+,x2=1﹣;
(2)3(x﹣2)2=x2﹣4,
3(x﹣2)2﹣(x+2)(x﹣2)=0,
(x﹣2)(3x﹣6﹣x﹣2)=0,
x﹣2=0或3x﹣6﹣x﹣2=0,
所以x1=2,x2=4.
19.(6分)如图是海洋公园娱乐设施“水上滑梯”的侧面图,建立如图坐标系.其中BC段可看成是反比例函数图象的一段,矩形AOEB为向上攀爬的梯子,梯子高6米,宽1米,出口C点到BE的距离CF为11米,求:
(1)BC段所在的反比例函数关系式是什么?
(2)C点到x轴的距离CD长是多少?
(3)若滑梯BC上有一个小球Q,Q的高度不高于3米,则Q到BE的距离至少多少米?
【分析】(1)根据矩形的性质得到BE=OA=6,AB=1,求得B(1,6),设双曲线BC的解析式为y=,得到k=6,于是得到结论;
(2)根据题意写出点C的横坐标,然后代入(1)中解析式求出y即可;
(3)令y≤3,解出x的取值范围即可.
【解答】解:(1)∵四边形AOEB是矩形,
∴BE=OA=6,AB=1,
∴B(1,6),
设双曲线BC的解析式为y=,
∴k=6,
∴BC段所在的反比例函数关系式是y=;
(2)∵CF=11,
∴点C的横坐标为12,
∴当x=12时,y==,
∴CD长为米;
(3)∵Q的高度不高于3米,即y≤3,
∴≤3,
解得x≥2,
∴x﹣1≥1,
∴Q到BE的距离至少1米,
20.(6分)小明和小红想去观看冬奥会开幕式,但只有一张入场券,于是他们设计了一个“配紫色”游戏:连续转动两个转盘,每个转盘被分成了面积相等的三个扇形,两人同时转动转盘,若其中一个转盘转出蓝色,另一个转盘转出红色,则可配成紫色.如果两次转盘转出的颜色相同或配成紫色,则小明去观看,否则小红去观看,你认为这个游戏对双方公平吗?
【分析】分别计算出小明观看和小红观看的概率,比较大小即可得出结论.
【解答】解:这个游戏对双方不公平,理由如下:
列表如下:
红 白 蓝
红 (红,红) (白,红) (蓝,红)
黄 (红,黄) (白,黄) (蓝,黄)
蓝 (红,蓝) (白,蓝) (蓝,蓝)
由表知,共有9种等可能结果,其中两次转盘转出的颜色相同或配成紫色的有4种结果,
∴小明去观看的概率为,
则小红去看的概率为1﹣=,
∵≠,
∴这个游戏对双方不公平.
21.(8分)已知:如图, ABCD中,F是AB中点,连接DF,DF延长线交CB的延长线于点E,连接AE.
求证:(1)△AFD≌△BFE;
(2)若BF=BC,∠EDC=60°,判断四边形AEBD的形状,并证明你的结论.
【分析】(1)根据ASA即可证明△AFD≌△BFE;
(2)结合(1)得出AD=EB,又AD∥EB,则四边形AEBD是平行四边形,根据BF=BC,∠EDC=60°,得△BFE是等边三角形,所以BF=EF=AF=DF,即可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠DAF=∠EBF,
∵点F是AB的中点,
∴AF=BF,
在△AFD和△BFE中,
,
∴△AFD≌△BFE(ASA);
(2)解:四边形AEBD是矩形,
证明:∵△AFD≌△BFE,
∴AD=EB,
∵AD∥EB,
∴四边形AEBD是平行四边形,
∴BE=DA=BC,
∵BF=BC,
∴BF=BE,
∵AB∥CD,
∴∠BFE=∠EDC=60°,
∴△BFE是等边三角形,
∴BF=EF=AF=DF,
∴AB=DE,
∴平行四边形AEBD是矩形.
22.(8分)如图1“海洋之星”摩天轮,是青岛最高的摩天轮.如图2,小刚从摩天轮最低处B出发沿水平方向向右行走15米到达C,再经过一段坡度为i=3:4,坡长为5米的斜坡CD到达点D,然后再沿水平方向向右行走一段时间后到达点E.在E处有一垂直地面的平台EF,测得EF=12米,在点F处,测得点D的俯角为52°,摩天轮最高处A的仰角为21°.AB所在的直线垂直于地面,垂足为O,点A、B、C、D、E、F、O在同一平面内,求AO的长度约为多少米?(结果精确到1米,参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.3,sin21°≈0.36,cos21°≈0.93,tan21°≈0.4)
【分析】过点C作CG⊥EO,垂足为G,过点F作FH⊥AO,垂足为H,根据题意可得:BC=GO=15米,FH=EO,EF=HO=12米,∠AFH=21°,∠HFD=52°,FH∥EO,从而利用平行线的性质可得∠FDE=52°,再根据已知可设CG=3k米,则DG=4k米,从而利用勾股定理进行计算求出DG=4米,然后在Rt△EFD中,利用锐角三角函数的定义求出DE的长,从而求出EO的长,最后在Rt△AFH中,利用锐角三角函数的定义求出AH的长,进行计算即可解答.
【解答】解:过点C作CG⊥EO,垂足为G,过点F作FH⊥AO,垂足为H,
由题意得:
BC=GO=15米,FH=EO,EF=HO=12米,∠AFH=21°,∠HFD=52°,FH∥EO,
∴∠HFD=∠FDE=52°,
∵斜坡CD的坡度为i=3:4,
∴=,
∴设CG=3k米,则DG=4k米,
∴CD===5k(米),
∵CD=5米,
∴5k=5,
∴k=1,
∴DG=4米,
在Rt△EFD中,EF=12米,
∴DE=≈≈9.2(米),
∴FH=EO=ED+DG+GO=9.2+4+15=28.2(米),
在Rt△AFH中,AH=FH tan21°≈28.2×0.4=11.28(米),
∴AO=AH+EF=11.28+12≈23(米),
∴AO的长度约为23米.
23.(10分)某公司销售一种商品,成本为4元/件,公司规定售价不能低于6元/件,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的几组对应数值如表:
销售单价x(元) 8 9 10 11 12
日销售量y(件) 80 75 70 65 60
(1)求出y与x之间的函数关系式;
(2)该商品的销售单价定为多少元,公司日销售此商品获得的利润最大?最大利润是多少元?
(3)若该商品的日销售量不少于70件,公司日销售此商品获得的最大利润是多少元?
【分析】(1)根据题中所给的表格中的数据,利用待定系数法可得其关系式;
(2)根据利润等于每件的利润乘以销售量列出函数解析式,根据函数的性质和自变量x的取值范围求函数最值;
(3)根据售价不能低于6元/件和该商品的日销售量不少于70件求出x的取值范围,再根据(2)中函数解析式,由函数的性质最值.
【解答】解:(1)设y与x的解析式为y=kx+b,
将(8,80)和(10,70)代入,
可得,
解得,
∴y与x之间的函数关系式为y=﹣5x+120;
(2)设公司销售该商品获得的日利润为w元,
w=(x﹣4)y=(x﹣4)(﹣5x+120)=﹣5x2+140x﹣480=﹣5(x﹣14)2+500,
∵x≥6,且﹣5x+120≥0,
∴6≤x≤24,
∵﹣5<0,
∴当x=14时,w有最大值,最大值为500,
答:该商品的销售单价定为14元,公司日销售此商品获得的利润最大,最大利润是500元;
(3)当﹣5x+120≥70时,
解得x≤10,
∴6≤x≤10,
由(2)知,w=﹣5(x﹣14)2+500,
∵﹣5<0,
∴当x<14时,w随x的增大而增大,
∴当x=10时,w最大,最大值为420,
答:该商品的日销售量不少于70件,公司日销售此商品获得的最大利润是420元.
24.(10分)探究一:在平面直角坐标系中探究的几何意义
例如:已知A(1,4),B(﹣4,﹣2),如果要求A、B两点之间的距离,可以构造如图1所示的直角三角形,则A、B之间的距离为 .
结论:在平面直角坐标系中,已知平面内A(x1,y1)、B(x2,y2)两点坐标,则A、B两点之间的距离等于因此,的几何意义可以理解为点A(x,y)与点B(a,b)之间的距离AB.
应用一:+的几何意义可以理解为点A(x,y)与点E( ﹣1 , ﹣2 )的距离和点A(x,y)与点F( ﹣3 , ﹣5 )的距离之和.
探究二:求代数式+的最小值.
解:+=+
如图2,建立平面直角坐标系,点P(x,0)是x轴上一点,则可以看成P(x,0)与点A( 0 , 2 )的距离.可以看成点P(x,0)与点B( 3 , 3 )的距离.
所以原代数式的值可以看成线段PA与PB的长度之和,PA+PB的最小值就是原代数式的最小值,设点A关于x轴的对称点为A',则PA=PA',因此求PA+PB的最小值,只需求PA'+PB的最小值.而点A'、B之间的所有连线中线段最短,所以PA'+PB的最小值为线段A'B的长度.为此,构造直角三角形A'CB,所以A'B= .
即+的最小值为 .
拓展:代数式+的最小值为 .
【分析】探究一:利用勾股定理求解即可;
应用一:利用勾股定理,数形结合的思想解决问题即可;
探究二:利用数形结合的思想,再根据轴对称的性质解决最短问题;
拓展:模仿例题解决问题即可.
【解答】解:探究一:AB==.
故答案为:;
应用一:+的几何意义可以理解为点A(x,y)与点E(﹣1,﹣2)的距离和点A(x,y)与点F(﹣3,﹣5)的距离之和.
故答案为:﹣1,﹣3,3,﹣5;
探究二:建立平面直角坐标系,点P(x,0)是x轴上一点,则可以看成P(x,0)与点A(0,2)的距离.可以看成点P(x,0)与点B(3,3)的距离.
所以原代数式的值可以看成线段PA与PB的长度之和,PA+PB的最小值就是原代数式的最小值,设点A关于x轴的对称点为A',则PA=PA',因此求PA+PB的最小值,只需求PA'+PB的最小值.而点A'、B之间的所有连线中线段最短,所以PA'+PB的最小值为线段A'B的长度.为此,构造直角三角形A'CB,所以A'B==.
即+的最小值为;
故答案为:0,2,3,3,,;
拓展:+=+,
欲求+的最小值,相当于在x轴上取一点Q(x,0),使得点Q到E(3,2),F(4,1)的距离和最小.
作点F关于x轴的对称点F′,连接EF′交x轴于点Q,连接FQ,此时QE+QF的值最小,最小值=EF′的长==.
故答案为:.
25.(10分)已知:如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=9cm,BC=25cm,CD=12cm,连接AC,点E从点B出发沿BC方向匀速运动,速度为4cm/s;同时,点F从点C出发沿CA方向匀速运动,速度为3cm/s.过点E作EG⊥AB交AB于点G,连接EF,当一点停止运动时,另一点也停止运动,设运动时间为t(s)(0<t<4).
(1)当点F在线段EC的垂直平分线上时,求t的值;
(2)当四边形AGEF是矩形时,求t的值;
(3)设四边形AGEF的面积为S(cm2),求S与t的函数关系式;
(4)取CD的中点Q,是否存在某一时刻t,使得点E、F、Q在同一条直线上?若存在,请求出t的值;若不存在,请说明理由.
【分析】(1)过点F作FH⊥BC于点H,由勾股定理求得AC,再证明△ACD∽△CFH,用t表示CH,由当点F在线段EC的垂直平分线上时,得CE=2CH,列出t的方程求得t的值便可;
(2)当四边形AGEF是矩形时,则EF∥AB,得△CEF∽△CBA,进而列出t的方程求解便可;
(3)先证明△ACD∽△CBA,得∠BAC=90°,求得AB,再证∴△BGE∽△BAC,用t表示BG,EG,FH,根据S=S△ABC﹣S△BEG﹣S△CEF得出结果便可;
(4)过Q点作PQ∥AD,与AC交于点P,如图,则PQ∥BC,当E、P、Q三点共线时,△PQF∽△CBF,根据相似三角形的性质列出t的方程,若方程有无解,则不存在某一时刻t,使得点E、F、Q在同一条直线上,若方程有解,则存在某一时刻t,使得点E、F、Q在同一条直线上,求得其解便可.
【解答】解:(1)过点F作FH⊥BC于点H,如图,
∵∠D=90°,AD=9cm,CD=12cm,
∴AC=15cm,
∵AD∥BC,
∴∠CAD=∠FCH,
∵∠D=∠CHF=90°,
∴△ACD∽△CFH,
∴,即,
∴CH=,
当点F在线段EC的垂直平分线上时,则CE=2CH,
即25﹣4t=t,
解得t=;
(2)当四边形AGEF是矩形时,则EF∥AB,
∴△CEF∽△CBA,
∴,即,
解得t=;
(3)∵AD=9cm,AC=15cm,BC=25cm,
∴,
∵∠CAD=∠BCA,
∴△ACD∽△CBA,
∴∠D=∠BAC=90°,
∴AB==20(cm),
∵EG⊥AB,
∴EG∥AC,
∴△BGE∽△BAC,
∴,即,
∴BG=t(cm),EG=t(cm),
∵FH=,
∴S=S△ABC﹣S△BEG﹣S△CEF===﹣,
即S=﹣(0≤t≤5);
(4)过Q点作PQ∥AD,与AC交于点P,如图,则PQ∥BC,
∵Q是CD的中点,
∴PC=PA=cm,PQ=AD=,
∴PF=CP﹣CF=﹣3t,
当E、P、Q三点共线时,
∵PQ∥BC,
∴△PQF∽△CBF,
∴,即,
整理得,8t2﹣79t+125=0,
解得t=>5(舍)或t=,
故存在某一时刻t=s时,使得点E、F、Q在同一条直线上.
一、单选题(本题满分24分,共8道小题,每小题3分)
1.(3分)方程x2=5x的解是( )
A.x=5 B.x=0 C.x1=﹣5;x2=0 D.x1=5;x2=0
2.(3分)将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的俯视图是( )
A. B. C. D.
3.(3分)如图,晚上小丽在路灯下散步,在小丽由A处走到B处的过程中,她在地上的影子( )
A.逐渐变长 B.逐渐变短
C.先变短后变长 D.先变长后变短
4.(3分)若点A(x1,﹣4),B(x2,2),C(x3,4)都在反比例函数y=的图象上,则x1、x2、x3的大小关系式( )
A.x1<x2<x3 B.x2<x3<x1 C.x3<x1<x2 D.x1<x3<x2
5.(3分)随着新冠疫苗的全民接种,疫苗需求仍存在较大缺口,某制药公司引进一条新冠疫苗生产线,开工第一天生产疫苗8000盒,第三天生产疫苗9680盒,若每天的增长率相同,求每天的增长率是多少?设每天的增长率是x,则可列方程为( )
A.8000x=9680
B.8000(1+x)=9680
C.8000(1+x)2=9680
D.8000+8000(1+x)+8000(1+x)2=9680
6.(3分)如图,在Rt△ABC中,∠C=90°,AB=5,cosA=,则tanB=( )
A. B. C. D.无法确定
7.(3分)如图,在正方形ABCD中,AB=9,点E、F分别在边AB、CD上,∠FEB=120°.若将四边形EBCF沿EF折叠,点C恰好落在AD边C'上,则C'D的长度为( )
A.3 B.3 C.3 D.
8.(3分)如图是二次函数y=ax2+bx的大致图象,则一次函数y=(a+b)x﹣b的图象大致是( )
A. B.
C. D.
二、填空题(本题满分24分,共8道小题,每小题3分)
9.(3分)计算:sin30°+tan30°= .
10.(3分)在一个不透明的口袋中装有6个黄球和n个白球,它们除颜色外完全相同,若从中随机摸出一球,摸到黄球的概率为,则n的值是 .
11.(3分)如图,在一块长32m、宽24米的矩形荒地上,要建造一个矩形花园,图中阴影部分是花园,并使花园所占面积为荒地面积的一半,花园外部四周修建宽度相同的小路,求图中的小路的宽是多少米?设小路的宽度为xm,所列方程式是 .
12.(3分)若二次函数y=﹣x2+4x﹣2m的图象与x轴没有交点,则m的取值范围是 .
13.(3分)如图,在菱形ABCD中,AB=12,∠BCD=60°,E是AD中点,BE交AC于点F,连接DF,则DF的长为 .
14.(3分)如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(﹣2,4),将△AOB绕点A顺时针旋转90°得到△ADC,点B的对应点C恰好落在反比例函数y=上,则k的值为 .
15.(3分)如图,四边形ABCD是矩形,点E在线段AD的延长线上,连接BE交CD于点F,∠BEC=2∠AEB,点G是BF的中点,若DE=1,BF=10,则AB的长为 .
16.(3分)如图1,是一座抛物线型拱桥侧面示意图,水面宽AB与桥长CD均为12m,在距离D点3m的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.如图2,桥面上方有3根高度均为5m的支柱CG、OH、DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为2m,下面结论正确的是 (填写正确结论序号).
①图1抛物线型拱桥的函数表达式y=﹣x2.
②图2右边钢缆抛物线的函数表达式y=2+2.
③图2左边钢缆抛物线的函数表达式y=2+2.
④图2在钢缆和桥拱之间竖直装饰若干条彩带,彩带长度的最小值是3m.
三、作图题(本题满分4分)用圆规、直尺作图,不写做法,但要保留作图痕迹
17.(4分)已知:△ABC中,E是AB上一点,求作:矩形EFGH,使FG在BC边上,H在AC边上.
四、解答题(本题共有8道小题,满分68分)
18.(10分)计算:
(1)2x2﹣4x+=0(配方法);
(2)3(x﹣2)2=x2﹣4(用适当方法).
19.(6分)如图是海洋公园娱乐设施“水上滑梯”的侧面图,建立如图坐标系.其中BC段可看成是反比例函数图象的一段,矩形AOEB为向上攀爬的梯子,梯子高6米,宽1米,出口C点到BE的距离CF为11米,求:
(1)BC段所在的反比例函数关系式是什么?
(2)C点到x轴的距离CD长是多少?
(3)若滑梯BC上有一个小球Q,Q的高度不高于3米,则Q到BE的距离至少多少米?
20.(6分)小明和小红想去观看冬奥会开幕式,但只有一张入场券,于是他们设计了一个“配紫色”游戏:连续转动两个转盘,每个转盘被分成了面积相等的三个扇形,两人同时转动转盘,若其中一个转盘转出蓝色,另一个转盘转出红色,则可配成紫色.如果两次转盘转出的颜色相同或配成紫色,则小明去观看,否则小红去观看,你认为这个游戏对双方公平吗?
21.(8分)已知:如图, ABCD中,F是AB中点,连接DF,DF延长线交CB的延长线于点E,连接AE.
求证:(1)△AFD≌△BFE;
(2)若BF=BC,∠EDC=60°,判断四边形AEBD的形状,并证明你的结论.
22.(8分)如图1“海洋之星”摩天轮,是青岛最高的摩天轮.如图2,小刚从摩天轮最低处B出发沿水平方向向右行走15米到达C,再经过一段坡度为i=3:4,坡长为5米的斜坡CD到达点D,然后再沿水平方向向右行走一段时间后到达点E.在E处有一垂直地面的平台EF,测得EF=12米,在点F处,测得点D的俯角为52°,摩天轮最高处A的仰角为21°.AB所在的直线垂直于地面,垂足为O,点A、B、C、D、E、F、O在同一平面内,求AO的长度约为多少米?(结果精确到1米,参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.3,sin21°≈0.36,cos21°≈0.93,tan21°≈0.4)
23.(10分)某公司销售一种商品,成本为4元/件,公司规定售价不能低于6元/件,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的几组对应数值如表:
销售单价x(元) 8 9 10 11 12
日销售量y(件) 80 75 70 65 60
(1)求出y与x之间的函数关系式;
(2)该商品的销售单价定为多少元,公司日销售此商品获得的利润最大?最大利润是多少元?
(3)若该商品的日销售量不少于70件,公司日销售此商品获得的最大利润是多少元?
24.(10分)探究一:在平面直角坐标系中探究的几何意义
例如:已知A(1,4),B(﹣4,﹣2),如果要求A、B两点之间的距离,可以构造如图1所示的直角三角形,则A、B之间的距离为 .
结论:在平面直角坐标系中,已知平面内A(x1,y1)、B(x2,y2)两点坐标,则A、B两点之间的距离等于因此,的几何意义可以理解为点A(x,y)与点B(a,b)之间的距离AB.
应用一:+的几何意义可以理解为点A(x,y)与点E( , )的距离和点A(x,y)与点F( , )的距离之和.
探究二:求代数式+的最小值.
解:+=+
如图2,建立平面直角坐标系,点P(x,0)是x轴上一点,则可以看成P(x,0)与点A( , )的距离.可以看成点P(x,0)与点B( , )的距离.
所以原代数式的值可以看成线段PA与PB的长度之和,PA+PB的最小值就是原代数式的最小值,设点A关于x轴的对称点为A',则PA=PA',因此求PA+PB的最小值,只需求PA'+PB的最小值.而点A'、B之间的所有连线中线段最短,所以PA'+PB的最小值为线段A'B的长度.为此,构造直角三角形A'CB,所以A'B= .
即+的最小值为 .
拓展:代数式+的最小值为 .
25.(10分)已知:如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=9cm,BC=25cm,CD=12cm,连接AC,点E从点B出发沿BC方向匀速运动,速度为4cm/s;同时,点F从点C出发沿CA方向匀速运动,速度为3cm/s.过点E作EG⊥AB交AB于点G,连接EF,当一点停止运动时,另一点也停止运动,设运动时间为t(s)(0<t<4).
(1)当点F在线段EC的垂直平分线上时,求t的值;
(2)当四边形AGEF是矩形时,求t的值;
(3)设四边形AGEF的面积为S(cm2),求S与t的函数关系式;
(4)取CD的中点Q,是否存在某一时刻t,使得点E、F、Q在同一条直线上?若存在,请求出t的值;若不存在,请说明理由.
2021-2022学年山东省青岛市城阳区九年级(上)期末数学试卷
参考答案与试题解析
一、单选题(本题满分24分,共8道小题,每小题3分)
1.(3分)方程x2=5x的解是( )
A.x=5 B.x=0 C.x1=﹣5;x2=0 D.x1=5;x2=0
【分析】先把方程化为一般式,然后利用因式分解法解方程.
【解答】解:x2﹣5x=0,
x(x﹣5)=0,
x=0或x﹣5=0,
所以x1=0,x2=5,
故选:D.
2.(3分)将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的俯视图是( )
A. B. C. D.
【分析】根据俯视图的画法画出它的俯视图即可.
【解答】解:这个几何体的俯视图为:
故选:C.
3.(3分)如图,晚上小丽在路灯下散步,在小丽由A处走到B处的过程中,她在地上的影子( )
A.逐渐变长 B.逐渐变短
C.先变短后变长 D.先变长后变短
【分析】小亮由A处径直路灯下,他得影子由长变短,再从路灯下到B处,他的影子则由短变长.
【解答】解:在小亮从A点走向B点的过程中,他在地上的影子先变短后变长.
故选:C.
4.(3分)若点A(x1,﹣4),B(x2,2),C(x3,4)都在反比例函数y=的图象上,则x1、x2、x3的大小关系式( )
A.x1<x2<x3 B.x2<x3<x1 C.x3<x1<x2 D.x1<x3<x2
【分析】解法一:直接将点A、B、C的坐标代入反比例函数y=中,求出x1、x2、x3,再比较大小即可.
解法二:根据反比例函数的图象和性质,结合点A、B、C纵坐标的数值,即可解答.
【解答】解法一:解:在反比例函数y=中,
当y=﹣4时,x1=﹣2,
当y=2时,x2=4,
当y=4时,x3=2,
∴x1<x3<x2.
故选:D.
解法二:解:在反比例函数y=中,k=8>0,
∴函数图象在一、三象限,在每个象限内,y随x的增大而减小,
∵点B、C在第一象限,且2<4,
∴x2>x3>0,
∵点A在第三象限,
∴x1<0,
∴x1<x3<x2,
故选:D.
5.(3分)随着新冠疫苗的全民接种,疫苗需求仍存在较大缺口,某制药公司引进一条新冠疫苗生产线,开工第一天生产疫苗8000盒,第三天生产疫苗9680盒,若每天的增长率相同,求每天的增长率是多少?设每天的增长率是x,则可列方程为( )
A.8000x=9680
B.8000(1+x)=9680
C.8000(1+x)2=9680
D.8000+8000(1+x)+8000(1+x)2=9680
【分析】利用第三天生产疫苗的数量=第一天生产疫苗的数量×(1+每天的增长率)2,即可得出关于x的一元二次方程,此题得解.
【解答】解:根据题意得8000(1+x)2=9680,
故选:C.
6.(3分)如图,在Rt△ABC中,∠C=90°,AB=5,cosA=,则tanB=( )
A. B. C. D.无法确定
【分析】根据锐角三角函数的定义求出AC,再根据勾股定理求出BC,由锐角三角函数的定义可得答案.
【解答】解:在Rt△ABC中,∠C=90°,
∵AB=5,cosA==,
∴AC=4,
∴BC==3,
∴tanB==,
故选:A.
7.(3分)如图,在正方形ABCD中,AB=9,点E、F分别在边AB、CD上,∠FEB=120°.若将四边形EBCF沿EF折叠,点C恰好落在AD边C'上,则C'D的长度为( )
A.3 B.3 C.3 D.
【分析】根据翻折的性质和正方形及勾股定理的有关性质求解.
【解答】解:在正方形ABCD中,CD=AB=9,CD∥AB,∠D=90°,
∴∠FEB+∠EFC=180°,
∴∠EFC=∠C′FE=60°,
∴∠C′FD=180°﹣∠EFC﹣∠C′FE=60°,
∴∠DC′F=30°,
∴C′F=2DF,
又∵C′F=CF,CF+DF=9,
∴DF=3,C′F=6,
∴C′D==3,
故选:B.
8.(3分)如图是二次函数y=ax2+bx的大致图象,则一次函数y=(a+b)x﹣b的图象大致是( )
A. B.
C. D.
【分析】根据二次函数的图象可以判断a、b、﹣b、a+b的正负情况,从而可以得到一次函数经过哪几个象限,本题得以解决.
【解答】解:由二次函数的图象可知,
a<0,b<0,
∴a+b<0,﹣b>0,
∴一次函数y=(a+b)x﹣b的图象在第一、二、四象限,
故选:B.
二、填空题(本题满分24分,共8道小题,每小题3分)
9.(3分)计算:sin30°+tan30°= 1 .
【分析】直接利用特殊角的三角函数值代入,进而计算得出答案.
【解答】解:原式=+×
=+
=1.
故答案为:1.
10.(3分)在一个不透明的口袋中装有6个黄球和n个白球,它们除颜色外完全相同,若从中随机摸出一球,摸到黄球的概率为,则n的值是 18 .
【分析】根据口袋中装有6个黄球和n个白球,故球的总个数为(6+n),再根据黄球的概率公式列式解答即可.
【解答】解:根据题意得:=,
解得n=18.
经检验,n=18是原分式方程的解.
故答案为:18.
11.(3分)如图,在一块长32m、宽24米的矩形荒地上,要建造一个矩形花园,图中阴影部分是花园,并使花园所占面积为荒地面积的一半,花园外部四周修建宽度相同的小路,求图中的小路的宽是多少米?设小路的宽度为xm,所列方程式是 (32﹣2x)(24﹣2x)=×32×24 .
【分析】根据小路的宽度,可得出矩形花园的长为(32﹣2x)m,宽为(24﹣2x)m,结合矩形花园所占面积为荒地面积的一半,即可得出关于x的一元二次方程,此题得解.
【解答】解:∵小路的宽度为xm,
∴矩形花园的长为(32﹣2x)m,宽为(24﹣2x)m.
根据题意得:(32﹣2x)(24﹣2x)=×32×24,
故答案为:(32﹣2x)(24﹣2x)=×32×24.
12.(3分)若二次函数y=﹣x2+4x﹣2m的图象与x轴没有交点,则m的取值范围是 m>2 .
【分析】利用判别式的意义得到Δ=42﹣4×(﹣1)×(﹣2m)<0,然后解不等式即可.
【解答】解:∵二次函数y=﹣x2+4x﹣2m的图象与x轴没有交点,
∴Δ=42﹣4×(﹣1)×(﹣2m)<0,
解得m>2.
故答案为:m>2.
13.(3分)如图,在菱形ABCD中,AB=12,∠BCD=60°,E是AD中点,BE交AC于点F,连接DF,则DF的长为 4 .
【分析】连接BD,则△ABD为等边三角形,点F为△ABD的外心,利用等边三角形的性质,可得出BE的长,由∠EDF=30°,可得出DF=2EF,进而可求出DF的长.
【解答】解:连接BD,则△ABD为等边三角形,点F为△ABD的外心,如图所示.
∵E是AD中点,AB=12,
∴BE⊥AD,AE=AB=×12=6,
∴BE===6.
又∵∠EDF=×60°=30°,
∴DF=2EF,
∴DF=BF=BE=×6=4.
故答案为:4.
14.(3分)如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(﹣2,4),将△AOB绕点A顺时针旋转90°得到△ADC,点B的对应点C恰好落在反比例函数y=上,则k的值为 ﹣24 .
【分析】根据题意和旋转的性质,可以得到点C的坐标,由点C恰好落在反比例函数y=上,从而可以得到k的值,本题得以解决.
【解答】解:∵OB在x轴上,∠ABO=90°,点A的坐标为(﹣2,4),将△AOB绕点A顺时针旋转90°得到△ADC,∴点C的坐标为(﹣6,4),
∵点B的对应点C恰好落在反比例函数y=上,
∴4=,
解得,k=﹣24,
故答案为:﹣24.
15.(3分)如图,四边形ABCD是矩形,点E在线段AD的延长线上,连接BE交CD于点F,∠BEC=2∠AEB,点G是BF的中点,若DE=1,BF=10,则AB的长为 2 .
【分析】根据直角三角形斜边上的中线等于斜边的一半可得BG=FG=GC=BF=5,然后根据等边对等角的性质可得∠GBC=∠GCB,再结合两直线平行,内错角相等可得∠GBC=∠AEB,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CGE=2∠AEB,从而得到∠BEC=∠CGE,再利用等角对等边的性质得到CE=CG,然后利用勾股定理列式计算即可得解.
【解答】解:∵四边形ABCD是矩形,
∴∠BCF=90°,
∵点G是BF的中点,
∴BG=FG=GC=BF=5,
∴∠GBC=∠GCB,
∵AD∥BC,
∴∠GBC=∠AEB,
∴∠CGE=∠GBC+∠GCB=2∠GBC=2∠AEB,
∵∠BEC=2∠AEB,
∴∠BEC=∠CGE,
∴CE=CG=5,
在Rt△CDE中,DE=1,
∴CD===2.
∴AB=CD=2.
故答案为:2.
16.(3分)如图1,是一座抛物线型拱桥侧面示意图,水面宽AB与桥长CD均为12m,在距离D点3m的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.如图2,桥面上方有3根高度均为5m的支柱CG、OH、DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为2m,下面结论正确的是 ①②③④ (填写正确结论序号).
①图1抛物线型拱桥的函数表达式y=﹣x2.
②图2右边钢缆抛物线的函数表达式y=2+2.
③图2左边钢缆抛物线的函数表达式y=2+2.
④图2在钢缆和桥拱之间竖直装饰若干条彩带,彩带长度的最小值是3m.
【分析】①利用待定系数法求函数解析式,然后结合二次函数图象上点的坐标特征计算求解;
②由图象分析右边钢缆所在抛物线的顶点坐标为(3,2),然后利用待定系数法求函数解析式;
③用与②相同的方法即可求出函数解析式;
④彩带的长度为Lm,利用L(x﹣3)2+2﹣(﹣x2)=(x﹣2)2+3,由函数的性质即可得出结论.
【解答】解:根据题意可知点F的坐标为(3,﹣1.5),
可设拱桥侧面所在二次函数表达式为:y1=a1x2,
将F(3,﹣1.5)代入y1=a1x2有:﹣1.5=9a1,
解得a1=﹣,
∴y1=﹣x2,
故①正确;
由题意可知右边钢缆所在抛物线的顶点坐标为(3,2),可设其表达式为y=a2(x﹣3)2+2,
将H(0,5)代入其表达式有:5=a2(0﹣3)2+2,
解得a2=,
∴右边钢缆所在抛物线表达式为:y=(x﹣3)2+2,
故②正确;
同理可知,③正确;
设彩带的长度为Lm,
则L=(x﹣3)2+2﹣(﹣x2)=x2﹣2x+5+x2=x2﹣2x+5=(x﹣2)2+3.
∵>0,
∴当x=2时,L最小,最小值为3.
故④正确.
故答案为:①②③④.
三、作图题(本题满分4分)用圆规、直尺作图,不写做法,但要保留作图痕迹
17.(4分)已知:△ABC中,E是AB上一点,求作:矩形EFGH,使FG在BC边上,H在AC边上.
【分析】根据要求作出图形即可.
【解答】解:如图,矩形EFGH即为所求.
四、解答题(本题共有8道小题,满分68分)
18.(10分)计算:
(1)2x2﹣4x+=0(配方法);
(2)3(x﹣2)2=x2﹣4(用适当方法).
【分析】(1)利用配方法得到(x﹣1)2=,然后利用直接开平方法解方程;
(2)先把方程化为3(x﹣2)2﹣(x+2)(x﹣2)=0,再利用因式分解法把方程转化为x﹣2=0或3x﹣6﹣x﹣2=0,然后解两个一次方程即可.
【解答】解:(1)2x2﹣4x+=0,
2x2﹣4x=﹣,
x2﹣2x=﹣,
x2﹣2x+1=﹣+1,
(x﹣1)2=,
x﹣1=±,
所以x1=1+,x2=1﹣;
(2)3(x﹣2)2=x2﹣4,
3(x﹣2)2﹣(x+2)(x﹣2)=0,
(x﹣2)(3x﹣6﹣x﹣2)=0,
x﹣2=0或3x﹣6﹣x﹣2=0,
所以x1=2,x2=4.
19.(6分)如图是海洋公园娱乐设施“水上滑梯”的侧面图,建立如图坐标系.其中BC段可看成是反比例函数图象的一段,矩形AOEB为向上攀爬的梯子,梯子高6米,宽1米,出口C点到BE的距离CF为11米,求:
(1)BC段所在的反比例函数关系式是什么?
(2)C点到x轴的距离CD长是多少?
(3)若滑梯BC上有一个小球Q,Q的高度不高于3米,则Q到BE的距离至少多少米?
【分析】(1)根据矩形的性质得到BE=OA=6,AB=1,求得B(1,6),设双曲线BC的解析式为y=,得到k=6,于是得到结论;
(2)根据题意写出点C的横坐标,然后代入(1)中解析式求出y即可;
(3)令y≤3,解出x的取值范围即可.
【解答】解:(1)∵四边形AOEB是矩形,
∴BE=OA=6,AB=1,
∴B(1,6),
设双曲线BC的解析式为y=,
∴k=6,
∴BC段所在的反比例函数关系式是y=;
(2)∵CF=11,
∴点C的横坐标为12,
∴当x=12时,y==,
∴CD长为米;
(3)∵Q的高度不高于3米,即y≤3,
∴≤3,
解得x≥2,
∴x﹣1≥1,
∴Q到BE的距离至少1米,
20.(6分)小明和小红想去观看冬奥会开幕式,但只有一张入场券,于是他们设计了一个“配紫色”游戏:连续转动两个转盘,每个转盘被分成了面积相等的三个扇形,两人同时转动转盘,若其中一个转盘转出蓝色,另一个转盘转出红色,则可配成紫色.如果两次转盘转出的颜色相同或配成紫色,则小明去观看,否则小红去观看,你认为这个游戏对双方公平吗?
【分析】分别计算出小明观看和小红观看的概率,比较大小即可得出结论.
【解答】解:这个游戏对双方不公平,理由如下:
列表如下:
红 白 蓝
红 (红,红) (白,红) (蓝,红)
黄 (红,黄) (白,黄) (蓝,黄)
蓝 (红,蓝) (白,蓝) (蓝,蓝)
由表知,共有9种等可能结果,其中两次转盘转出的颜色相同或配成紫色的有4种结果,
∴小明去观看的概率为,
则小红去看的概率为1﹣=,
∵≠,
∴这个游戏对双方不公平.
21.(8分)已知:如图, ABCD中,F是AB中点,连接DF,DF延长线交CB的延长线于点E,连接AE.
求证:(1)△AFD≌△BFE;
(2)若BF=BC,∠EDC=60°,判断四边形AEBD的形状,并证明你的结论.
【分析】(1)根据ASA即可证明△AFD≌△BFE;
(2)结合(1)得出AD=EB,又AD∥EB,则四边形AEBD是平行四边形,根据BF=BC,∠EDC=60°,得△BFE是等边三角形,所以BF=EF=AF=DF,即可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠DAF=∠EBF,
∵点F是AB的中点,
∴AF=BF,
在△AFD和△BFE中,
,
∴△AFD≌△BFE(ASA);
(2)解:四边形AEBD是矩形,
证明:∵△AFD≌△BFE,
∴AD=EB,
∵AD∥EB,
∴四边形AEBD是平行四边形,
∴BE=DA=BC,
∵BF=BC,
∴BF=BE,
∵AB∥CD,
∴∠BFE=∠EDC=60°,
∴△BFE是等边三角形,
∴BF=EF=AF=DF,
∴AB=DE,
∴平行四边形AEBD是矩形.
22.(8分)如图1“海洋之星”摩天轮,是青岛最高的摩天轮.如图2,小刚从摩天轮最低处B出发沿水平方向向右行走15米到达C,再经过一段坡度为i=3:4,坡长为5米的斜坡CD到达点D,然后再沿水平方向向右行走一段时间后到达点E.在E处有一垂直地面的平台EF,测得EF=12米,在点F处,测得点D的俯角为52°,摩天轮最高处A的仰角为21°.AB所在的直线垂直于地面,垂足为O,点A、B、C、D、E、F、O在同一平面内,求AO的长度约为多少米?(结果精确到1米,参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.3,sin21°≈0.36,cos21°≈0.93,tan21°≈0.4)
【分析】过点C作CG⊥EO,垂足为G,过点F作FH⊥AO,垂足为H,根据题意可得:BC=GO=15米,FH=EO,EF=HO=12米,∠AFH=21°,∠HFD=52°,FH∥EO,从而利用平行线的性质可得∠FDE=52°,再根据已知可设CG=3k米,则DG=4k米,从而利用勾股定理进行计算求出DG=4米,然后在Rt△EFD中,利用锐角三角函数的定义求出DE的长,从而求出EO的长,最后在Rt△AFH中,利用锐角三角函数的定义求出AH的长,进行计算即可解答.
【解答】解:过点C作CG⊥EO,垂足为G,过点F作FH⊥AO,垂足为H,
由题意得:
BC=GO=15米,FH=EO,EF=HO=12米,∠AFH=21°,∠HFD=52°,FH∥EO,
∴∠HFD=∠FDE=52°,
∵斜坡CD的坡度为i=3:4,
∴=,
∴设CG=3k米,则DG=4k米,
∴CD===5k(米),
∵CD=5米,
∴5k=5,
∴k=1,
∴DG=4米,
在Rt△EFD中,EF=12米,
∴DE=≈≈9.2(米),
∴FH=EO=ED+DG+GO=9.2+4+15=28.2(米),
在Rt△AFH中,AH=FH tan21°≈28.2×0.4=11.28(米),
∴AO=AH+EF=11.28+12≈23(米),
∴AO的长度约为23米.
23.(10分)某公司销售一种商品,成本为4元/件,公司规定售价不能低于6元/件,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的几组对应数值如表:
销售单价x(元) 8 9 10 11 12
日销售量y(件) 80 75 70 65 60
(1)求出y与x之间的函数关系式;
(2)该商品的销售单价定为多少元,公司日销售此商品获得的利润最大?最大利润是多少元?
(3)若该商品的日销售量不少于70件,公司日销售此商品获得的最大利润是多少元?
【分析】(1)根据题中所给的表格中的数据,利用待定系数法可得其关系式;
(2)根据利润等于每件的利润乘以销售量列出函数解析式,根据函数的性质和自变量x的取值范围求函数最值;
(3)根据售价不能低于6元/件和该商品的日销售量不少于70件求出x的取值范围,再根据(2)中函数解析式,由函数的性质最值.
【解答】解:(1)设y与x的解析式为y=kx+b,
将(8,80)和(10,70)代入,
可得,
解得,
∴y与x之间的函数关系式为y=﹣5x+120;
(2)设公司销售该商品获得的日利润为w元,
w=(x﹣4)y=(x﹣4)(﹣5x+120)=﹣5x2+140x﹣480=﹣5(x﹣14)2+500,
∵x≥6,且﹣5x+120≥0,
∴6≤x≤24,
∵﹣5<0,
∴当x=14时,w有最大值,最大值为500,
答:该商品的销售单价定为14元,公司日销售此商品获得的利润最大,最大利润是500元;
(3)当﹣5x+120≥70时,
解得x≤10,
∴6≤x≤10,
由(2)知,w=﹣5(x﹣14)2+500,
∵﹣5<0,
∴当x<14时,w随x的增大而增大,
∴当x=10时,w最大,最大值为420,
答:该商品的日销售量不少于70件,公司日销售此商品获得的最大利润是420元.
24.(10分)探究一:在平面直角坐标系中探究的几何意义
例如:已知A(1,4),B(﹣4,﹣2),如果要求A、B两点之间的距离,可以构造如图1所示的直角三角形,则A、B之间的距离为 .
结论:在平面直角坐标系中,已知平面内A(x1,y1)、B(x2,y2)两点坐标,则A、B两点之间的距离等于因此,的几何意义可以理解为点A(x,y)与点B(a,b)之间的距离AB.
应用一:+的几何意义可以理解为点A(x,y)与点E( ﹣1 , ﹣2 )的距离和点A(x,y)与点F( ﹣3 , ﹣5 )的距离之和.
探究二:求代数式+的最小值.
解:+=+
如图2,建立平面直角坐标系,点P(x,0)是x轴上一点,则可以看成P(x,0)与点A( 0 , 2 )的距离.可以看成点P(x,0)与点B( 3 , 3 )的距离.
所以原代数式的值可以看成线段PA与PB的长度之和,PA+PB的最小值就是原代数式的最小值,设点A关于x轴的对称点为A',则PA=PA',因此求PA+PB的最小值,只需求PA'+PB的最小值.而点A'、B之间的所有连线中线段最短,所以PA'+PB的最小值为线段A'B的长度.为此,构造直角三角形A'CB,所以A'B= .
即+的最小值为 .
拓展:代数式+的最小值为 .
【分析】探究一:利用勾股定理求解即可;
应用一:利用勾股定理,数形结合的思想解决问题即可;
探究二:利用数形结合的思想,再根据轴对称的性质解决最短问题;
拓展:模仿例题解决问题即可.
【解答】解:探究一:AB==.
故答案为:;
应用一:+的几何意义可以理解为点A(x,y)与点E(﹣1,﹣2)的距离和点A(x,y)与点F(﹣3,﹣5)的距离之和.
故答案为:﹣1,﹣3,3,﹣5;
探究二:建立平面直角坐标系,点P(x,0)是x轴上一点,则可以看成P(x,0)与点A(0,2)的距离.可以看成点P(x,0)与点B(3,3)的距离.
所以原代数式的值可以看成线段PA与PB的长度之和,PA+PB的最小值就是原代数式的最小值,设点A关于x轴的对称点为A',则PA=PA',因此求PA+PB的最小值,只需求PA'+PB的最小值.而点A'、B之间的所有连线中线段最短,所以PA'+PB的最小值为线段A'B的长度.为此,构造直角三角形A'CB,所以A'B==.
即+的最小值为;
故答案为:0,2,3,3,,;
拓展:+=+,
欲求+的最小值,相当于在x轴上取一点Q(x,0),使得点Q到E(3,2),F(4,1)的距离和最小.
作点F关于x轴的对称点F′,连接EF′交x轴于点Q,连接FQ,此时QE+QF的值最小,最小值=EF′的长==.
故答案为:.
25.(10分)已知:如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=9cm,BC=25cm,CD=12cm,连接AC,点E从点B出发沿BC方向匀速运动,速度为4cm/s;同时,点F从点C出发沿CA方向匀速运动,速度为3cm/s.过点E作EG⊥AB交AB于点G,连接EF,当一点停止运动时,另一点也停止运动,设运动时间为t(s)(0<t<4).
(1)当点F在线段EC的垂直平分线上时,求t的值;
(2)当四边形AGEF是矩形时,求t的值;
(3)设四边形AGEF的面积为S(cm2),求S与t的函数关系式;
(4)取CD的中点Q,是否存在某一时刻t,使得点E、F、Q在同一条直线上?若存在,请求出t的值;若不存在,请说明理由.
【分析】(1)过点F作FH⊥BC于点H,由勾股定理求得AC,再证明△ACD∽△CFH,用t表示CH,由当点F在线段EC的垂直平分线上时,得CE=2CH,列出t的方程求得t的值便可;
(2)当四边形AGEF是矩形时,则EF∥AB,得△CEF∽△CBA,进而列出t的方程求解便可;
(3)先证明△ACD∽△CBA,得∠BAC=90°,求得AB,再证∴△BGE∽△BAC,用t表示BG,EG,FH,根据S=S△ABC﹣S△BEG﹣S△CEF得出结果便可;
(4)过Q点作PQ∥AD,与AC交于点P,如图,则PQ∥BC,当E、P、Q三点共线时,△PQF∽△CBF,根据相似三角形的性质列出t的方程,若方程有无解,则不存在某一时刻t,使得点E、F、Q在同一条直线上,若方程有解,则存在某一时刻t,使得点E、F、Q在同一条直线上,求得其解便可.
【解答】解:(1)过点F作FH⊥BC于点H,如图,
∵∠D=90°,AD=9cm,CD=12cm,
∴AC=15cm,
∵AD∥BC,
∴∠CAD=∠FCH,
∵∠D=∠CHF=90°,
∴△ACD∽△CFH,
∴,即,
∴CH=,
当点F在线段EC的垂直平分线上时,则CE=2CH,
即25﹣4t=t,
解得t=;
(2)当四边形AGEF是矩形时,则EF∥AB,
∴△CEF∽△CBA,
∴,即,
解得t=;
(3)∵AD=9cm,AC=15cm,BC=25cm,
∴,
∵∠CAD=∠BCA,
∴△ACD∽△CBA,
∴∠D=∠BAC=90°,
∴AB==20(cm),
∵EG⊥AB,
∴EG∥AC,
∴△BGE∽△BAC,
∴,即,
∴BG=t(cm),EG=t(cm),
∵FH=,
∴S=S△ABC﹣S△BEG﹣S△CEF===﹣,
即S=﹣(0≤t≤5);
(4)过Q点作PQ∥AD,与AC交于点P,如图,则PQ∥BC,
∵Q是CD的中点,
∴PC=PA=cm,PQ=AD=,
∴PF=CP﹣CF=﹣3t,
当E、P、Q三点共线时,
∵PQ∥BC,
∴△PQF∽△CBF,
∴,即,
整理得,8t2﹣79t+125=0,
解得t=>5(舍)或t=,
故存在某一时刻t=s时,使得点E、F、Q在同一条直线上.
同课章节目录
