2021-2022学年上海市普陀区七校联考八年级(上)期末数学试卷 (含解析)
文档属性
| 名称 | 2021-2022学年上海市普陀区七校联考八年级(上)期末数学试卷 (含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 342.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-27 00:00:00 | ||
图片预览




文档简介
2021-2022学年上海市普陀区七校联考八年级(上)期末数学试卷
一、选择题:(本大题共6题,每题3分,满分18分)
1.(3分)下列各式中与是同类二次根式的是( )
A. B. C. D.
2.(3分)下列各式中,是的有理化因式的是( )
A. B. C. D.
3.(3分)如果关于x的一元二次方程(m﹣1)x2+5x+m2﹣1=0的常数项为0,那么m的值等于( )
A.1 或﹣1 B.1 C.﹣1 D.0
4.(3分)下列函数中,y的值随着x的值增大而减小的是( )
A.y= B.y=﹣2x C.y=﹣ D.y=2x
5.(3分)用下列几组边长构成的三角形中哪一组不是直角三角形( )
A.8,15,17 B.,, C.,2, D.1,2,
6.(3分)下列命题的逆命题错误的是( )
A.线段垂直平分线上的任意一点到这条线段两个端点的距离相等
B.全等三角形的三条边对应相等
C.如果两个角都是直角,那么这两个角相等
D.等边三角形每个内角都等于60°
二、填空题:(本大题共12题,每题2分,满分24分)
7.(2分)化简:(x>0)= .
8.(2分)函数的定义域是 .
9.(2分)方程:x(x﹣1)=2x的根是 .
10.(2分)不解方程,判别方程3x2+4x=﹣2的根的情况: .
11.(2分)在实数范围内分解因式:2x2﹣4x﹣2= .
12.(2分)已知:f(x)=,那么f(0)= .
13.(2分)某商店八月份的营业额是100万元,预计十月份的营业额可达到144万元,如果九、十月份营业额的月增长率相同,那么这个商店营业额的月增长率为 .
14.(2分)已知点A(x1,y1)和点B(x2,y2)在反比例函数y=(k<0)的图象上,且x1<0<x2,判断y1、y2的大小关系:y1 y2.(填“>”、“=”、“<”)
15.(2分)如图,△ABC中,AB=AC,∠A=50°,AB边的垂直平分线交AC于点D,交AB于点E,则∠DBC= .
16.(2分)如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于H,如果CH=AC,那么∠B= 度.
17.(2分)若直角三角形中有两边长分别为6和8,那么第三边长应该为 .
18.(2分)如图,△ABC中,∠C=50°,将△ABC绕着点A顺时针旋转到△ADE的位置,此时,点E正好落在边BC上,那么∠BED= 度.
三、解答题(本大题共4题,满分24分)
19.(6分)计算:﹣+6.
20.(6分)解方程:x(x﹣)=3x﹣4.
21.(6分)已知关于x的一元二次方程mx2﹣(3m﹣1)x+2m=1(m为常数).如果方程根的判别式为1,求m的值及该方程的根.
22.(6分)已知,如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,且BD=CD.求证:AB=AC.
四、解答题(本大题共4题,第23-25题每题8分,第26题10分,满分34分)
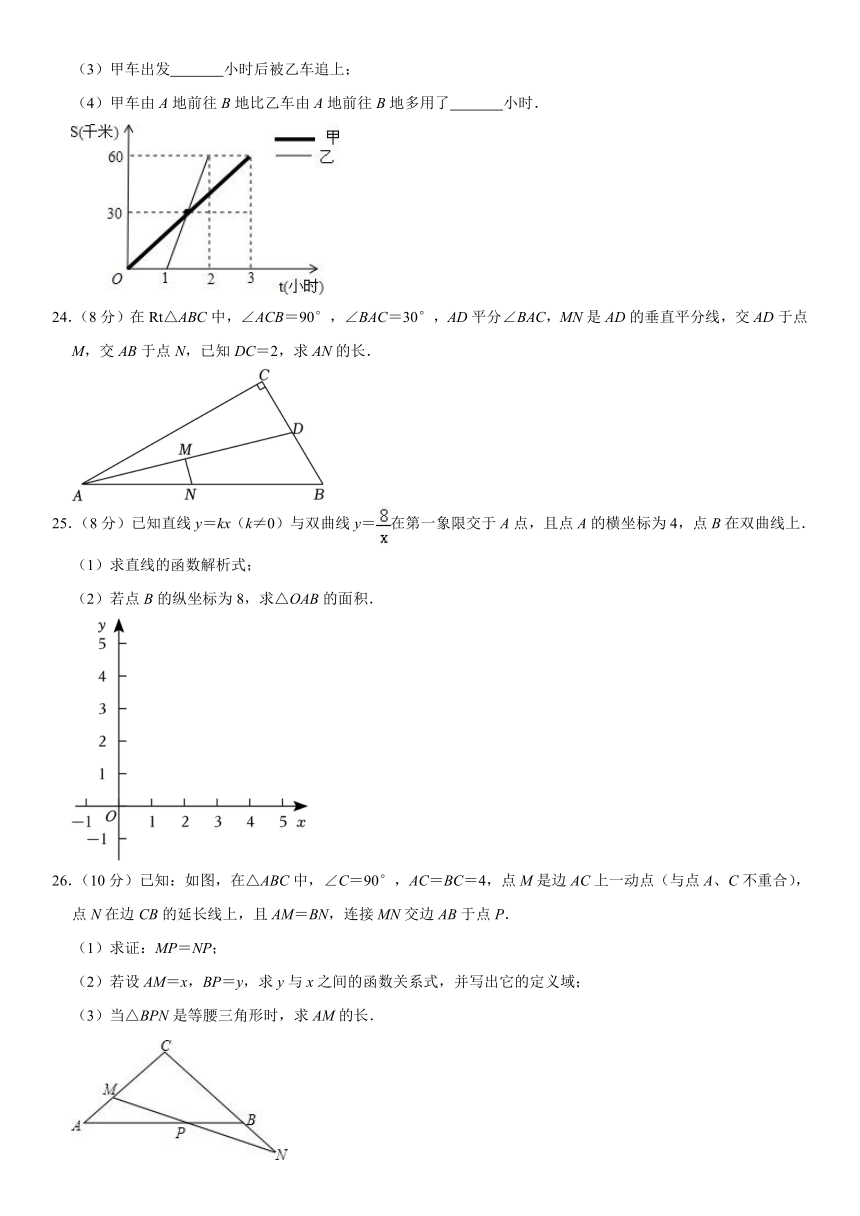
23.(8分)甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
(1)A地与B地之间的距离是 千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式是 ;
(3)甲车出发 小时后被乙车追上;
(4)甲车由A地前往B地比乙车由A地前往B地多用了 小时.
24.(8分)在Rt△ABC中,∠ACB=90°,∠BAC=30°,AD平分∠BAC,MN是AD的垂直平分线,交AD于点M,交AB于点N,已知DC=2,求AN的长.
25.(8分)已知直线y=kx(k≠0)与双曲线y=在第一象限交于A点,且点A的横坐标为4,点B在双曲线上.
(1)求直线的函数解析式;
(2)若点B的纵坐标为8,求△OAB的面积.
26.(10分)已知:如图,在△ABC中,∠C=90°,AC=BC=4,点M是边AC上一动点(与点A、C不重合),点N在边CB的延长线上,且AM=BN,连接MN交边AB于点P.
(1)求证:MP=NP;
(2)若设AM=x,BP=y,求y与x之间的函数关系式,并写出它的定义域;
(3)当△BPN是等腰三角形时,求AM的长.
2021-2022学年上海市普陀区七校联考八年级(上)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共6题,每题3分,满分18分)
1.(3分)下列各式中与是同类二次根式的是( )
A. B. C. D.
【分析】化简二次根式,即可判定.
【解答】解:A、与不是同类二次根式;
B、与是同类二次根式;
C、与不是同类二次根式;
D、与不是同类二次根式;
故选:B.
2.(3分)下列各式中,是的有理化因式的是( )
A. B. C. D.
【分析】根据有理化因式的定义逐个判断即可.
【解答】解:的有理化因式是a﹣2.
故选:D.
3.(3分)如果关于x的一元二次方程(m﹣1)x2+5x+m2﹣1=0的常数项为0,那么m的值等于( )
A.1 或﹣1 B.1 C.﹣1 D.0
【分析】利用一元二次方程的定义判断即可.
【解答】解:∵关于x的一元二次方程(m﹣1)x2+5x+m2﹣1=0的常数项为0,
∴m2﹣1=0且m﹣1≠0,
解得:m=﹣1,
故选:C.
4.(3分)下列函数中,y的值随着x的值增大而减小的是( )
A.y= B.y=﹣2x C.y=﹣ D.y=2x
【分析】根据正比例函数、反比例函数的增减性,结合自变量的取值范围,逐一判断.
【解答】解:A、y=是反比例函数,∵2>0,故在每一象限内y随x的增大而减小,不符合题意;
B、y=﹣2x是正比例函数,k=﹣2<0,故y随着x增大而减小,符合题意;
C、y=是反比例函数,∵﹣2<0,故在第一象限内y随x的增大而减小,不符合题意;
D、y=2x,正比例函数,k>0,故y随着x增大而增大,不符合题意;
故选:B.
5.(3分)用下列几组边长构成的三角形中哪一组不是直角三角形( )
A.8,15,17 B.,, C.,2, D.1,2,
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.
【解答】解:A、∵82+152=172,∴此三角形为直角三角形,故选项错误;
B、∵()2+()2=()2,∴此三角形是直角三角形,故选项错误;
C、∵()2+22≠()2,∴此三角形不是直角三角形,故选项正确;
D、∵12+22=()2,∴此三角形为直角三角形,故选项错误.
故选:C.
6.(3分)下列命题的逆命题错误的是( )
A.线段垂直平分线上的任意一点到这条线段两个端点的距离相等
B.全等三角形的三条边对应相等
C.如果两个角都是直角,那么这两个角相等
D.等边三角形每个内角都等于60°
【分析】写出原命题的逆命题后判断正误即可.
【解答】解:A、逆命题为到线段两端点距离相等的点在线段的垂直平分线上,正确,不符合题意;
B、逆命题为三条边对应相等的两个三角形全等,正确,不符合题意;
C、逆命题为相等的两个角为直角,错误,符合题意;
D、逆命题为三个内角都为60°的三角形是等边三角形,正确,不符合题意.
故选:C.
二、填空题:(本大题共12题,每题2分,满分24分)
7.(2分)化简:(x>0)= 3x .
【分析】根据二次根式的性质化简,即可解答.
【解答】解:=.
故答案为:3x.
8.(2分)函数的定义域是 x≥3 .
【分析】根据二次根式的性质的意义,被开方数大于或等于0,可以求出x的范围.
【解答】解:根据题意得:x﹣3≥0,
解得:x≥3.
故答案为x≥3.
9.(2分)方程:x(x﹣1)=2x的根是 0或3 .
【分析】先移项,然后利用提取公因式法对等式的左边进行因式分解,最后解方程即可.
【解答】解:由原方程,得
x(x﹣1﹣2)=0,即x(x﹣3)=0,
所以x=0或x﹣3=0,
解得x1=0,x2=3,
故答案是:0或3.
10.(2分)不解方程,判别方程3x2+4x=﹣2的根的情况: 方程没有实数根 .
【分析】判断上述方程的根的情况,只要看根的判别式Δ=b2﹣4ac的值的符号就可以了.
【解答】解:∵3x2+4x=﹣2,
∴3x2+4x+2=0,
∵Δ=42﹣4×3×2=﹣8<0,
∴方程没有实数根.
故答案为:方程没有实数根.
11.(2分)在实数范围内分解因式:2x2﹣4x﹣2= 2(x﹣1﹣)(x﹣1+) .
【分析】先提公因式,再求出相应方程的根,即可进行因式分解.
【解答】解:∵2x2﹣4x﹣2=2(x2﹣2x﹣1).
又∵x2﹣2x﹣1=0的根为x1=1+,x2=1﹣.
则2x2﹣4x﹣2=2(x2﹣2x﹣1)=2(x﹣1﹣)(x﹣1+).
故答案为2(x﹣1﹣)(x﹣1+).
12.(2分)已知:f(x)=,那么f(0)= 6 .
【分析】直接利用已知公式将x的值代入求出答案.
【解答】解:∵f(x)=,
∴f(0)==6.
故答案为:6.
13.(2分)某商店八月份的营业额是100万元,预计十月份的营业额可达到144万元,如果九、十月份营业额的月增长率相同,那么这个商店营业额的月增长率为 20% .
【分析】设这个商店营业额的月增长率为x,关系式为:8月份的营业额×(1+增长率)2=10月份的营业额,把相关数值代入计算即可.
【解答】解:设这个商店营业额的月增长率为x,依题意有
100×(1+x)2=144,
(1+x)2=1.44,
∵1+x>0,
∴1+x=1.2,
x=0.2=20%.
故答案为:20%.
14.(2分)已知点A(x1,y1)和点B(x2,y2)在反比例函数y=(k<0)的图象上,且x1<0<x2,判断y1、y2的大小关系:y1 > y2.(填“>”、“=”、“<”)
【分析】首先根据函数关系式画出草图,然后根据图象可直接得到y1、y2、y3的大小关系.
【解答】解:反比例函数y=(k<0)的图象上经过第二、四象限,
如图所示:∵x1<0<x2,
∴y1>y2.
故答案为:>.
15.(2分)如图,△ABC中,AB=AC,∠A=50°,AB边的垂直平分线交AC于点D,交AB于点E,则∠DBC= 15° .
【分析】先根据等腰三角形的性质求出∠ABC的度数,再由线段垂直平分线的性质得出∠A=∠ABD,进而可得出结论.
【解答】解:∵在△ABC中,∠A=50°,AB=AC,
∴∠ABC=(180°﹣∠A)=65°.
∵AB边的垂直平分线交AC于点D,交AB于点E,
∴AD=BD,
∴∠ABD=∠A=50°,
∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°.
故答案为15°.
16.(2分)如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于H,如果CH=AC,那么∠B= 60 度.
【分析】根据垂直定义可得∠AHC=90°,然后在Rt△AHC中,利用含30度角的直角三角形的性质可得∠A=30°,从而利用直角三角形的两个锐角互余进行计算即可解答.
【解答】解:∵CH⊥AB,
∴∠AHC=90°,
∵CH=AC,
∴∠A=30°,
∵∠ACB=90°,
∴∠B=90°﹣∠A=60°,
故答案为:60.
17.(2分)若直角三角形中有两边长分别为6和8,那么第三边长应该为 10或2 .
【分析】分8是直角边和8是斜边两种情况,根据勾股定理计算.
【解答】解:当8是直角边时,第三边长==10,
当8是斜边时,第三边长==2,
故答案为:10或2.
18.(2分)如图,△ABC中,∠C=50°,将△ABC绕着点A顺时针旋转到△ADE的位置,此时,点E正好落在边BC上,那么∠BED= 80 度.
【分析】先根据旋转的性质得出△ADE≌△ABC,则∠AED=∠C,AE=AC,再由等边对等角得出∠AEC=∠C,然后根据平角的定义即可求得∠BED的度数.
【解答】解:∵将△ABC绕着点A顺时针旋转到△ADE的位置,
∴△ADE≌△ABC,
∴∠AED=∠C=50°,AE=AC,
∴∠AEC=∠C=50°,
∴∠BED=180°﹣(∠AED+∠AEC)=180°﹣(50°+50°)=80°.
故答案是:80.
三、解答题(本大题共4题,满分24分)
19.(6分)计算:﹣+6.
【分析】先分母有理化,然后把各二次根式化为最简二次根式后合并即可.
【解答】解:原式=5+2++2
=8+2.
20.(6分)解方程:x(x﹣)=3x﹣4.
【分析】方程去括号,去分母整理后,利用因式分解法求出解即可.
【解答】解:去括号得:x2﹣4x=3x﹣4,
去分母得:3x2﹣8x=6x﹣8,即3x2﹣14x+8=0,
分解因式得:(x﹣4)(3x﹣2)=0,
解得x1=4,x2=.
21.(6分)已知关于x的一元二次方程mx2﹣(3m﹣1)x+2m=1(m为常数).如果方程根的判别式为1,求m的值及该方程的根.
【分析】由一元二次方程的Δ=b2﹣4ac=1,建立m的方程,求出m的解.
【解答】解:原方程化为mx2﹣(3m﹣1)x+2m﹣1=0,
∵关于x的一元二次方程根的判别式为1,
∴m≠0,Δ=b2﹣4ac=[﹣(3m﹣1)]2﹣4m(2m﹣1)=1,
解得:m1=0(不符合题意,舍去),m2=2,
∴原方程化为:2x2﹣5x+3=0,
∴x1=1,x2=.
22.(6分)已知,如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,且BD=CD.求证:AB=AC.
【分析】欲证明AB=AC,利用全等三角形的性质证明∠B=∠C即可;
【解答】证明:∵AD平分∠BAC(已知),
∴∠EAD=∠FAD(角平分线的定义),
∵DE⊥AB,DF⊥AC (已知),
∴∠DEA=∠DFA(垂直的意义),
又∵AD=AD(公共边),
∴△AED≌△AFD(AAS),
∴DE=DF(全等三角形对应边相等),
∵DB=DC(已知),∠BED=∠DFC=90°,
∴Rt△BED≌Rt△CFD(HL),
∴∠B=∠C(全等三角形对应角相等),
∴AB=AC(等角对等边).
四、解答题(本大题共4题,第23-25题每题8分,第26题10分,满分34分)
23.(8分)甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
(1)A地与B地之间的距离是 60 千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式是 s=20t ;
(3)甲车出发 1.5 小时后被乙车追上;
(4)甲车由A地前往B地比乙车由A地前往B地多用了 2 小时.
【分析】(1)由图象直接得出A地与B地之间的距离是60千米;
(2)设s与t的函数解析式是s=kt,代入(3,60),得出答案即可;
(3)甲车的函数解析式建立方程求得答案即可;
(4)由图象两车由A地前往B地所用时间,再进一步得出答案即可.
【解答】解:(1)A地与B地之间的距离是60千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式是乙车由A地前往B地时所对应的s与t的函数解析式,代入(3,60),得s=20t;
(3)由题意可知20t=30,
解得t=1.5.
所以甲车出发1.5小时后被乙车追上;
(4)甲车由A地前往B地比乙车由A地前往B地多用了3﹣1=2小时.
24.(8分)在Rt△ABC中,∠ACB=90°,∠BAC=30°,AD平分∠BAC,MN是AD的垂直平分线,交AD于点M,交AB于点N,已知DC=2,求AN的长.
【分析】过D作DE⊥AB于点E,连接DN,依据角平分线的性质可得CD=DE;根据线段垂直平分线的性质可得AN=DN;再根据30°角的直角三角形的性质即可得到DN的长,进而得出结论.
【解答】解:如图所示,过D作DE⊥AB于点E,连接DN,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=CD=2,
∵∠BAC=30°,AD平分∠BAC,
∴∠BAD=15°,
∵MN是AD的垂直平分线,
∴NA=ND,
∴∠ADN=∠NAD=15°,
∴∠DNE=30°,
∴DN=2DE=4,
∴AN=4.
25.(8分)已知直线y=kx(k≠0)与双曲线y=在第一象限交于A点,且点A的横坐标为4,点B在双曲线上.
(1)求直线的函数解析式;
(2)若点B的纵坐标为8,求△OAB的面积.
【分析】(1)将A点横坐标x=4代入y=中,得A点纵坐标y=2,可知点A的坐标为(4,2),再将A(4,2)代入y=kx,求k即可;
(2)点B在双曲线y=上,将y=8代入得x=1,即B(1,8),已知A(4,2),O(0,0),根据两点间距离公式分别求OA,AB,OB,利用勾股定理的逆定理证明△OAB是直角三角形,然后根据△OAB的面积为=求得即可.
【解答】解:(1)将x=4代入y=,得y=2,
∴点A的坐标为(4,2),
将A(4,2)代入y=kx(k≠0),得k=,
∴直线的函数解析式为y=x;
(2)△OAB是直角三角形.
理由:y=8代入y=中,得x=1,
∴B点的坐标为(1,8),
又A(4,2),O(0,0),
由两点间距离公式得OA=2,AB=3,OB=,
∵OA2+AB2=20+45=65=OB2,
∴△OAB是直角三角形,
∴△OAB的面积为:=×3=15.
26.(10分)已知:如图,在△ABC中,∠C=90°,AC=BC=4,点M是边AC上一动点(与点A、C不重合),点N在边CB的延长线上,且AM=BN,连接MN交边AB于点P.
(1)求证:MP=NP;
(2)若设AM=x,BP=y,求y与x之间的函数关系式,并写出它的定义域;
(3)当△BPN是等腰三角形时,求AM的长.
【分析】(1)过点M作MD∥BC交AB于点D,求出DM=BN,证△MDP≌△NBP即可;
(2)求出AB,根据△MDP≌△NBP推出DP=BP,推出方程即可;
(3)求出BP=BN,所得方程的解即可.
【解答】(1)证明:过点M作MD∥BC交AB于点D,
∵MD∥BC,
∴∠MDP=∠NBP,
∵AC=BC,∠C=90°,
∴∠A=∠ABC=45°,
∵MD∥BC,
∴∠ADM=∠ABC=45°,
∴∠ADM=∠A,
∴AM=DM.
∵AM=BN,
∴BN=DM,
在△MDP和△NBP中
,
∴△MDP≌△NBP,
∴MP=NP.
(2)解:在Rt△ABC中,
∵∠C=90°,AC=BC=4,
∴.
∵MD∥BC,
∴∠AMD=∠C=90°.
在Rt△ADM中,AM=DM=x,
∴.
∵△MDP≌△NBP,
∴DP=BP=y,
∵AD+DP+PB=AB,
∴,
∴所求的函数解析式为,
定义域为0<x<4.
答:y与x之间的函数关系式为,它的定义域是0<x<4.
(3)解:∵△MDP≌△NBP,
∴BN=MD=x.
∵∠ABC+∠PBN=180°,∠ABC=45°,
∴∠PBN=135°.
∴当△BPN是等腰三角形时,只有BP=BN,即x=y.
∴,
解得,
∴当△BPN是等腰三角形时,AM的长为.
答:AM的长为.
一、选择题:(本大题共6题,每题3分,满分18分)
1.(3分)下列各式中与是同类二次根式的是( )
A. B. C. D.
2.(3分)下列各式中,是的有理化因式的是( )
A. B. C. D.
3.(3分)如果关于x的一元二次方程(m﹣1)x2+5x+m2﹣1=0的常数项为0,那么m的值等于( )
A.1 或﹣1 B.1 C.﹣1 D.0
4.(3分)下列函数中,y的值随着x的值增大而减小的是( )
A.y= B.y=﹣2x C.y=﹣ D.y=2x
5.(3分)用下列几组边长构成的三角形中哪一组不是直角三角形( )
A.8,15,17 B.,, C.,2, D.1,2,
6.(3分)下列命题的逆命题错误的是( )
A.线段垂直平分线上的任意一点到这条线段两个端点的距离相等
B.全等三角形的三条边对应相等
C.如果两个角都是直角,那么这两个角相等
D.等边三角形每个内角都等于60°
二、填空题:(本大题共12题,每题2分,满分24分)
7.(2分)化简:(x>0)= .
8.(2分)函数的定义域是 .
9.(2分)方程:x(x﹣1)=2x的根是 .
10.(2分)不解方程,判别方程3x2+4x=﹣2的根的情况: .
11.(2分)在实数范围内分解因式:2x2﹣4x﹣2= .
12.(2分)已知:f(x)=,那么f(0)= .
13.(2分)某商店八月份的营业额是100万元,预计十月份的营业额可达到144万元,如果九、十月份营业额的月增长率相同,那么这个商店营业额的月增长率为 .
14.(2分)已知点A(x1,y1)和点B(x2,y2)在反比例函数y=(k<0)的图象上,且x1<0<x2,判断y1、y2的大小关系:y1 y2.(填“>”、“=”、“<”)
15.(2分)如图,△ABC中,AB=AC,∠A=50°,AB边的垂直平分线交AC于点D,交AB于点E,则∠DBC= .
16.(2分)如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于H,如果CH=AC,那么∠B= 度.
17.(2分)若直角三角形中有两边长分别为6和8,那么第三边长应该为 .
18.(2分)如图,△ABC中,∠C=50°,将△ABC绕着点A顺时针旋转到△ADE的位置,此时,点E正好落在边BC上,那么∠BED= 度.
三、解答题(本大题共4题,满分24分)
19.(6分)计算:﹣+6.
20.(6分)解方程:x(x﹣)=3x﹣4.
21.(6分)已知关于x的一元二次方程mx2﹣(3m﹣1)x+2m=1(m为常数).如果方程根的判别式为1,求m的值及该方程的根.
22.(6分)已知,如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,且BD=CD.求证:AB=AC.
四、解答题(本大题共4题,第23-25题每题8分,第26题10分,满分34分)
23.(8分)甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
(1)A地与B地之间的距离是 千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式是 ;
(3)甲车出发 小时后被乙车追上;
(4)甲车由A地前往B地比乙车由A地前往B地多用了 小时.
24.(8分)在Rt△ABC中,∠ACB=90°,∠BAC=30°,AD平分∠BAC,MN是AD的垂直平分线,交AD于点M,交AB于点N,已知DC=2,求AN的长.
25.(8分)已知直线y=kx(k≠0)与双曲线y=在第一象限交于A点,且点A的横坐标为4,点B在双曲线上.
(1)求直线的函数解析式;
(2)若点B的纵坐标为8,求△OAB的面积.
26.(10分)已知:如图,在△ABC中,∠C=90°,AC=BC=4,点M是边AC上一动点(与点A、C不重合),点N在边CB的延长线上,且AM=BN,连接MN交边AB于点P.
(1)求证:MP=NP;
(2)若设AM=x,BP=y,求y与x之间的函数关系式,并写出它的定义域;
(3)当△BPN是等腰三角形时,求AM的长.
2021-2022学年上海市普陀区七校联考八年级(上)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共6题,每题3分,满分18分)
1.(3分)下列各式中与是同类二次根式的是( )
A. B. C. D.
【分析】化简二次根式,即可判定.
【解答】解:A、与不是同类二次根式;
B、与是同类二次根式;
C、与不是同类二次根式;
D、与不是同类二次根式;
故选:B.
2.(3分)下列各式中,是的有理化因式的是( )
A. B. C. D.
【分析】根据有理化因式的定义逐个判断即可.
【解答】解:的有理化因式是a﹣2.
故选:D.
3.(3分)如果关于x的一元二次方程(m﹣1)x2+5x+m2﹣1=0的常数项为0,那么m的值等于( )
A.1 或﹣1 B.1 C.﹣1 D.0
【分析】利用一元二次方程的定义判断即可.
【解答】解:∵关于x的一元二次方程(m﹣1)x2+5x+m2﹣1=0的常数项为0,
∴m2﹣1=0且m﹣1≠0,
解得:m=﹣1,
故选:C.
4.(3分)下列函数中,y的值随着x的值增大而减小的是( )
A.y= B.y=﹣2x C.y=﹣ D.y=2x
【分析】根据正比例函数、反比例函数的增减性,结合自变量的取值范围,逐一判断.
【解答】解:A、y=是反比例函数,∵2>0,故在每一象限内y随x的增大而减小,不符合题意;
B、y=﹣2x是正比例函数,k=﹣2<0,故y随着x增大而减小,符合题意;
C、y=是反比例函数,∵﹣2<0,故在第一象限内y随x的增大而减小,不符合题意;
D、y=2x,正比例函数,k>0,故y随着x增大而增大,不符合题意;
故选:B.
5.(3分)用下列几组边长构成的三角形中哪一组不是直角三角形( )
A.8,15,17 B.,, C.,2, D.1,2,
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.
【解答】解:A、∵82+152=172,∴此三角形为直角三角形,故选项错误;
B、∵()2+()2=()2,∴此三角形是直角三角形,故选项错误;
C、∵()2+22≠()2,∴此三角形不是直角三角形,故选项正确;
D、∵12+22=()2,∴此三角形为直角三角形,故选项错误.
故选:C.
6.(3分)下列命题的逆命题错误的是( )
A.线段垂直平分线上的任意一点到这条线段两个端点的距离相等
B.全等三角形的三条边对应相等
C.如果两个角都是直角,那么这两个角相等
D.等边三角形每个内角都等于60°
【分析】写出原命题的逆命题后判断正误即可.
【解答】解:A、逆命题为到线段两端点距离相等的点在线段的垂直平分线上,正确,不符合题意;
B、逆命题为三条边对应相等的两个三角形全等,正确,不符合题意;
C、逆命题为相等的两个角为直角,错误,符合题意;
D、逆命题为三个内角都为60°的三角形是等边三角形,正确,不符合题意.
故选:C.
二、填空题:(本大题共12题,每题2分,满分24分)
7.(2分)化简:(x>0)= 3x .
【分析】根据二次根式的性质化简,即可解答.
【解答】解:=.
故答案为:3x.
8.(2分)函数的定义域是 x≥3 .
【分析】根据二次根式的性质的意义,被开方数大于或等于0,可以求出x的范围.
【解答】解:根据题意得:x﹣3≥0,
解得:x≥3.
故答案为x≥3.
9.(2分)方程:x(x﹣1)=2x的根是 0或3 .
【分析】先移项,然后利用提取公因式法对等式的左边进行因式分解,最后解方程即可.
【解答】解:由原方程,得
x(x﹣1﹣2)=0,即x(x﹣3)=0,
所以x=0或x﹣3=0,
解得x1=0,x2=3,
故答案是:0或3.
10.(2分)不解方程,判别方程3x2+4x=﹣2的根的情况: 方程没有实数根 .
【分析】判断上述方程的根的情况,只要看根的判别式Δ=b2﹣4ac的值的符号就可以了.
【解答】解:∵3x2+4x=﹣2,
∴3x2+4x+2=0,
∵Δ=42﹣4×3×2=﹣8<0,
∴方程没有实数根.
故答案为:方程没有实数根.
11.(2分)在实数范围内分解因式:2x2﹣4x﹣2= 2(x﹣1﹣)(x﹣1+) .
【分析】先提公因式,再求出相应方程的根,即可进行因式分解.
【解答】解:∵2x2﹣4x﹣2=2(x2﹣2x﹣1).
又∵x2﹣2x﹣1=0的根为x1=1+,x2=1﹣.
则2x2﹣4x﹣2=2(x2﹣2x﹣1)=2(x﹣1﹣)(x﹣1+).
故答案为2(x﹣1﹣)(x﹣1+).
12.(2分)已知:f(x)=,那么f(0)= 6 .
【分析】直接利用已知公式将x的值代入求出答案.
【解答】解:∵f(x)=,
∴f(0)==6.
故答案为:6.
13.(2分)某商店八月份的营业额是100万元,预计十月份的营业额可达到144万元,如果九、十月份营业额的月增长率相同,那么这个商店营业额的月增长率为 20% .
【分析】设这个商店营业额的月增长率为x,关系式为:8月份的营业额×(1+增长率)2=10月份的营业额,把相关数值代入计算即可.
【解答】解:设这个商店营业额的月增长率为x,依题意有
100×(1+x)2=144,
(1+x)2=1.44,
∵1+x>0,
∴1+x=1.2,
x=0.2=20%.
故答案为:20%.
14.(2分)已知点A(x1,y1)和点B(x2,y2)在反比例函数y=(k<0)的图象上,且x1<0<x2,判断y1、y2的大小关系:y1 > y2.(填“>”、“=”、“<”)
【分析】首先根据函数关系式画出草图,然后根据图象可直接得到y1、y2、y3的大小关系.
【解答】解:反比例函数y=(k<0)的图象上经过第二、四象限,
如图所示:∵x1<0<x2,
∴y1>y2.
故答案为:>.
15.(2分)如图,△ABC中,AB=AC,∠A=50°,AB边的垂直平分线交AC于点D,交AB于点E,则∠DBC= 15° .
【分析】先根据等腰三角形的性质求出∠ABC的度数,再由线段垂直平分线的性质得出∠A=∠ABD,进而可得出结论.
【解答】解:∵在△ABC中,∠A=50°,AB=AC,
∴∠ABC=(180°﹣∠A)=65°.
∵AB边的垂直平分线交AC于点D,交AB于点E,
∴AD=BD,
∴∠ABD=∠A=50°,
∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°.
故答案为15°.
16.(2分)如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于H,如果CH=AC,那么∠B= 60 度.
【分析】根据垂直定义可得∠AHC=90°,然后在Rt△AHC中,利用含30度角的直角三角形的性质可得∠A=30°,从而利用直角三角形的两个锐角互余进行计算即可解答.
【解答】解:∵CH⊥AB,
∴∠AHC=90°,
∵CH=AC,
∴∠A=30°,
∵∠ACB=90°,
∴∠B=90°﹣∠A=60°,
故答案为:60.
17.(2分)若直角三角形中有两边长分别为6和8,那么第三边长应该为 10或2 .
【分析】分8是直角边和8是斜边两种情况,根据勾股定理计算.
【解答】解:当8是直角边时,第三边长==10,
当8是斜边时,第三边长==2,
故答案为:10或2.
18.(2分)如图,△ABC中,∠C=50°,将△ABC绕着点A顺时针旋转到△ADE的位置,此时,点E正好落在边BC上,那么∠BED= 80 度.
【分析】先根据旋转的性质得出△ADE≌△ABC,则∠AED=∠C,AE=AC,再由等边对等角得出∠AEC=∠C,然后根据平角的定义即可求得∠BED的度数.
【解答】解:∵将△ABC绕着点A顺时针旋转到△ADE的位置,
∴△ADE≌△ABC,
∴∠AED=∠C=50°,AE=AC,
∴∠AEC=∠C=50°,
∴∠BED=180°﹣(∠AED+∠AEC)=180°﹣(50°+50°)=80°.
故答案是:80.
三、解答题(本大题共4题,满分24分)
19.(6分)计算:﹣+6.
【分析】先分母有理化,然后把各二次根式化为最简二次根式后合并即可.
【解答】解:原式=5+2++2
=8+2.
20.(6分)解方程:x(x﹣)=3x﹣4.
【分析】方程去括号,去分母整理后,利用因式分解法求出解即可.
【解答】解:去括号得:x2﹣4x=3x﹣4,
去分母得:3x2﹣8x=6x﹣8,即3x2﹣14x+8=0,
分解因式得:(x﹣4)(3x﹣2)=0,
解得x1=4,x2=.
21.(6分)已知关于x的一元二次方程mx2﹣(3m﹣1)x+2m=1(m为常数).如果方程根的判别式为1,求m的值及该方程的根.
【分析】由一元二次方程的Δ=b2﹣4ac=1,建立m的方程,求出m的解.
【解答】解:原方程化为mx2﹣(3m﹣1)x+2m﹣1=0,
∵关于x的一元二次方程根的判别式为1,
∴m≠0,Δ=b2﹣4ac=[﹣(3m﹣1)]2﹣4m(2m﹣1)=1,
解得:m1=0(不符合题意,舍去),m2=2,
∴原方程化为:2x2﹣5x+3=0,
∴x1=1,x2=.
22.(6分)已知,如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,且BD=CD.求证:AB=AC.
【分析】欲证明AB=AC,利用全等三角形的性质证明∠B=∠C即可;
【解答】证明:∵AD平分∠BAC(已知),
∴∠EAD=∠FAD(角平分线的定义),
∵DE⊥AB,DF⊥AC (已知),
∴∠DEA=∠DFA(垂直的意义),
又∵AD=AD(公共边),
∴△AED≌△AFD(AAS),
∴DE=DF(全等三角形对应边相等),
∵DB=DC(已知),∠BED=∠DFC=90°,
∴Rt△BED≌Rt△CFD(HL),
∴∠B=∠C(全等三角形对应角相等),
∴AB=AC(等角对等边).
四、解答题(本大题共4题,第23-25题每题8分,第26题10分,满分34分)
23.(8分)甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
(1)A地与B地之间的距离是 60 千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式是 s=20t ;
(3)甲车出发 1.5 小时后被乙车追上;
(4)甲车由A地前往B地比乙车由A地前往B地多用了 2 小时.
【分析】(1)由图象直接得出A地与B地之间的距离是60千米;
(2)设s与t的函数解析式是s=kt,代入(3,60),得出答案即可;
(3)甲车的函数解析式建立方程求得答案即可;
(4)由图象两车由A地前往B地所用时间,再进一步得出答案即可.
【解答】解:(1)A地与B地之间的距离是60千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式是乙车由A地前往B地时所对应的s与t的函数解析式,代入(3,60),得s=20t;
(3)由题意可知20t=30,
解得t=1.5.
所以甲车出发1.5小时后被乙车追上;
(4)甲车由A地前往B地比乙车由A地前往B地多用了3﹣1=2小时.
24.(8分)在Rt△ABC中,∠ACB=90°,∠BAC=30°,AD平分∠BAC,MN是AD的垂直平分线,交AD于点M,交AB于点N,已知DC=2,求AN的长.
【分析】过D作DE⊥AB于点E,连接DN,依据角平分线的性质可得CD=DE;根据线段垂直平分线的性质可得AN=DN;再根据30°角的直角三角形的性质即可得到DN的长,进而得出结论.
【解答】解:如图所示,过D作DE⊥AB于点E,连接DN,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=CD=2,
∵∠BAC=30°,AD平分∠BAC,
∴∠BAD=15°,
∵MN是AD的垂直平分线,
∴NA=ND,
∴∠ADN=∠NAD=15°,
∴∠DNE=30°,
∴DN=2DE=4,
∴AN=4.
25.(8分)已知直线y=kx(k≠0)与双曲线y=在第一象限交于A点,且点A的横坐标为4,点B在双曲线上.
(1)求直线的函数解析式;
(2)若点B的纵坐标为8,求△OAB的面积.
【分析】(1)将A点横坐标x=4代入y=中,得A点纵坐标y=2,可知点A的坐标为(4,2),再将A(4,2)代入y=kx,求k即可;
(2)点B在双曲线y=上,将y=8代入得x=1,即B(1,8),已知A(4,2),O(0,0),根据两点间距离公式分别求OA,AB,OB,利用勾股定理的逆定理证明△OAB是直角三角形,然后根据△OAB的面积为=求得即可.
【解答】解:(1)将x=4代入y=,得y=2,
∴点A的坐标为(4,2),
将A(4,2)代入y=kx(k≠0),得k=,
∴直线的函数解析式为y=x;
(2)△OAB是直角三角形.
理由:y=8代入y=中,得x=1,
∴B点的坐标为(1,8),
又A(4,2),O(0,0),
由两点间距离公式得OA=2,AB=3,OB=,
∵OA2+AB2=20+45=65=OB2,
∴△OAB是直角三角形,
∴△OAB的面积为:=×3=15.
26.(10分)已知:如图,在△ABC中,∠C=90°,AC=BC=4,点M是边AC上一动点(与点A、C不重合),点N在边CB的延长线上,且AM=BN,连接MN交边AB于点P.
(1)求证:MP=NP;
(2)若设AM=x,BP=y,求y与x之间的函数关系式,并写出它的定义域;
(3)当△BPN是等腰三角形时,求AM的长.
【分析】(1)过点M作MD∥BC交AB于点D,求出DM=BN,证△MDP≌△NBP即可;
(2)求出AB,根据△MDP≌△NBP推出DP=BP,推出方程即可;
(3)求出BP=BN,所得方程的解即可.
【解答】(1)证明:过点M作MD∥BC交AB于点D,
∵MD∥BC,
∴∠MDP=∠NBP,
∵AC=BC,∠C=90°,
∴∠A=∠ABC=45°,
∵MD∥BC,
∴∠ADM=∠ABC=45°,
∴∠ADM=∠A,
∴AM=DM.
∵AM=BN,
∴BN=DM,
在△MDP和△NBP中
,
∴△MDP≌△NBP,
∴MP=NP.
(2)解:在Rt△ABC中,
∵∠C=90°,AC=BC=4,
∴.
∵MD∥BC,
∴∠AMD=∠C=90°.
在Rt△ADM中,AM=DM=x,
∴.
∵△MDP≌△NBP,
∴DP=BP=y,
∵AD+DP+PB=AB,
∴,
∴所求的函数解析式为,
定义域为0<x<4.
答:y与x之间的函数关系式为,它的定义域是0<x<4.
(3)解:∵△MDP≌△NBP,
∴BN=MD=x.
∵∠ABC+∠PBN=180°,∠ABC=45°,
∴∠PBN=135°.
∴当△BPN是等腰三角形时,只有BP=BN,即x=y.
∴,
解得,
∴当△BPN是等腰三角形时,AM的长为.
答:AM的长为.
同课章节目录
