2022-2023学年安徽省淮南市谢家集区八年级(上)期中数学试卷 ( word含解析版)
文档属性
| 名称 | 2022-2023学年安徽省淮南市谢家集区八年级(上)期中数学试卷 ( word含解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-27 09:03:32 | ||
图片预览


文档简介
2022-2023学年安徽省淮南市谢家集区八年级(上)期中数学试卷
一、选择题(本题共10小题,每小题3分,满分30分)下列各题的四个选项中,只有一个是正确的。
1.下列卡通动物简笔画图案中,属于轴对称图形的是( )
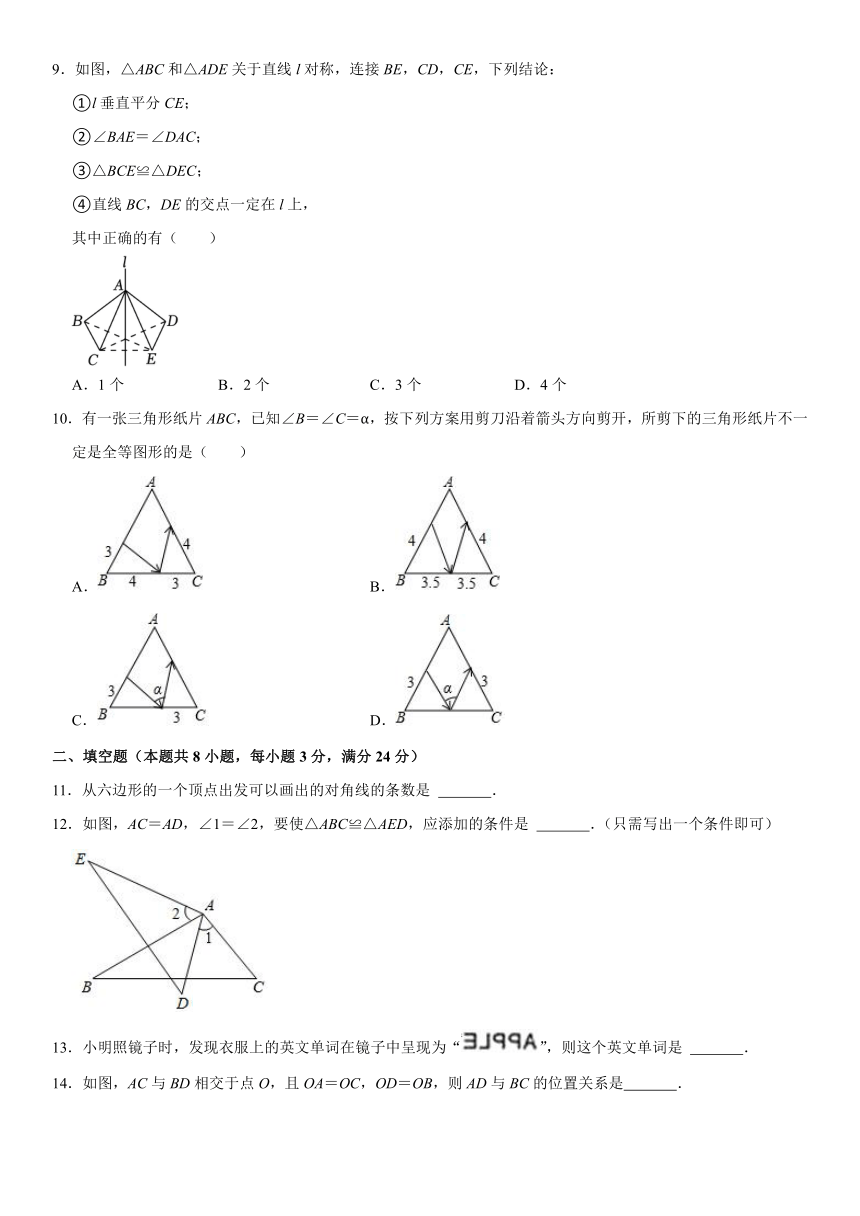
A. B.
C. D.
2.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为( )
A.120° B.80° C.60° D.40°
3.在平面直角坐标系xOy中,点M(﹣3,2)关于x轴对称的点的坐标是( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
4.一个三角形的两边长分别为3和7,且第三边的边长为整数,这样的三角形的周长的最小值是( )
A.14 B.15 C.16 D.17
5.一个多边形的内角和是外角和的3倍,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
6.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=28°,则∠A的度数为( )
A.34° B.36° C.38° D.40°
7.下列说法中,错误的是( )
A.全等三角形对应边上的中线相等
B.一个锐角和斜边对应相等的两个直角三角形全等
C.到直线I的距离相等的两个点关于直线l对称
D.三角形的一条中线将三角形分成两个面积相等的三角形
8.如图,在五边形ABCDE中,若∠E=120°,则∠1+∠2+∠3+∠4的度数为( )
A.280° B.300° C.320° D.340°
9.如图,△ABC和△ADE关于直线l对称,连接BE,CD,CE,下列结论:
①l垂直平分CE;
②∠BAE=∠DAC;
③△BCE≌△DEC;
④直线BC,DE的交点一定在l上,
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.有一张三角形纸片ABC,已知∠B=∠C=α,按下列方案用剪刀沿着箭头方向剪开,所剪下的三角形纸片不一定是全等图形的是( )
A. B.
C. D.
二、填空题(本题共8小题,每小题3分,满分24分)
11.从六边形的一个顶点出发可以画出的对角线的条数是 .
12.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是 .(只需写出一个条件即可)
13.小明照镜子时,发现衣服上的英文单词在镜子中呈现为“”,则这个英文单词是 .
14.如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系是 .
15.已知点A(a+1,2)关于y轴的对称点为B(3,b﹣1),则a+b的值为 .
16.如图,在△ABC中,AB的垂直平分线交AB于点E,交边AC于点D,若BC=6cm,△BCD
的周长为14cm,则AC的长为 .
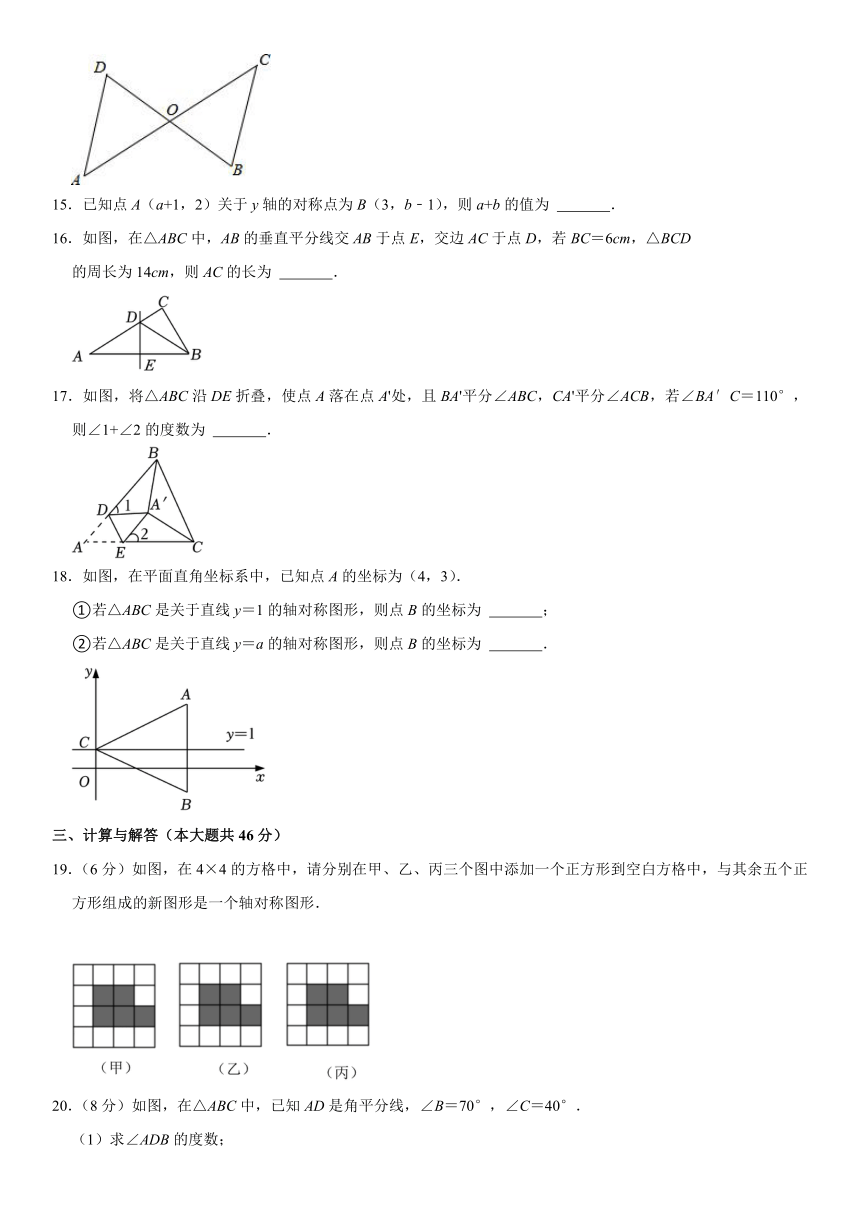
17.如图,将△ABC沿DE折叠,使点A落在点A'处,且BA'平分∠ABC,CA'平分∠ACB,若∠BA′C=110°,则∠1+∠2的度数为 .
18.如图,在平面直角坐标系中,已知点A的坐标为(4,3).
①若△ABC是关于直线y=1的轴对称图形,则点B的坐标为 ;
②若△ABC是关于直线y=a的轴对称图形,则点B的坐标为 .
三、计算与解答(本大题共46分)
19.(6分)如图,在4×4的方格中,请分别在甲、乙、丙三个图中添加一个正方形到空白方格中,与其余五个正方形组成的新图形是一个轴对称图形.
20.(8分)如图,在△ABC中,已知AD是角平分线,∠B=70°,∠C=40°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
21.(8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE并延
长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AD=2,AB=5,当BC的长为 时,点B在线段AF的垂直平分线上.
22.(10分)如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点)和直线l.
(1)在直线l上找一点P,使点P到边AB,BC的距离相等;
(2)画出OABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位长度,画出平移后得到的图形△A2B2C2;
(3)结合轴对称变换和平移变换的有关性质,两个对应图形△ABC和△A2B2C2的对应点所具有的性质是 .
A.对应点连线互相平行
B.对应点连线被直线l垂直平分
C.对应点连线被直线l平分或与直线l重合
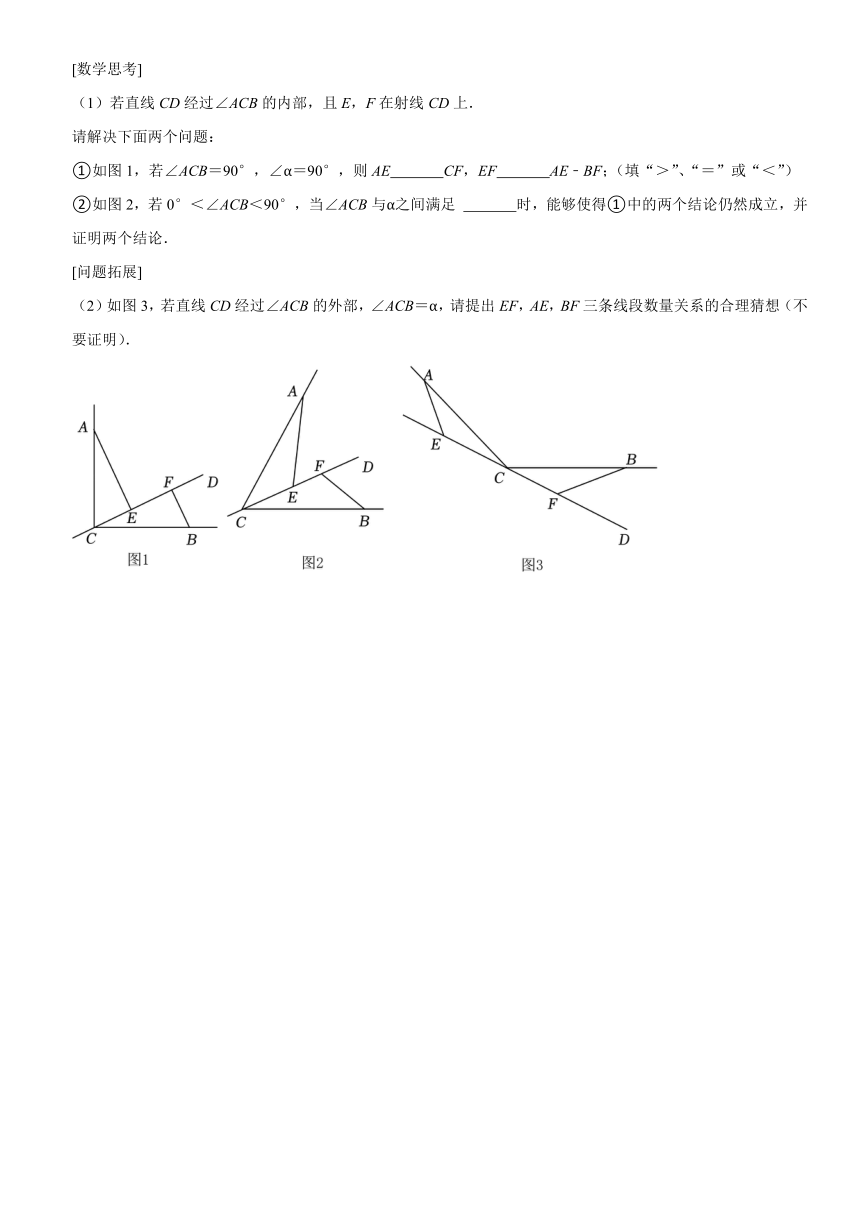
23.(14分)如图,CD是经过∠ACB顶点C的一条直线,AC=CB,E,F分别是直线CD.上两点,且∠AEC=∠CFB=α.
[数学思考]
(1)若直线CD经过∠ACB的内部,且E,F在射线CD上.
请解决下面两个问题:
①如图1,若∠ACB=90°,∠α=90°,则AE CF,EF AE﹣BF;(填“>”、“=”或“<”)
②如图2,若0°<∠ACB<90°,当∠ACB与α之间满足 时,能够使得①中的两个结论仍然成立,并证明两个结论.
[问题拓展]
(2)如图3,若直线CD经过∠ACB的外部,∠ACB=α,请提出EF,AE,BF三条线段数量关系的合理猜想(不要证明).
2022-2023学年安徽省淮南市谢家集区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题共10小题,每小题3分,满分30分)下列各题的四个选项中,只有一个是正确的。
1.下列卡通动物简笔画图案中,属于轴对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选:D.
2.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为( )
A.120° B.80° C.60° D.40°
【分析】直接用一个未知数表示出∠A,∠B,∠C的度数,再利用三角形内角和定理得出答案.
【解答】解:∵∠A:∠B:∠C=2:3:4,
∴设∠A=2x,∠B=3x,∠C=4x,
∵∠A+∠B+∠C=180°,
∴2x+3x+4x=180°,
解得:x=20°,
∴∠B的度数为:60°.
故选:C.
3.在平面直角坐标系xOy中,点M(﹣3,2)关于x轴对称的点的坐标是( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
【分析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答即可.
【解答】解:点M(﹣3,2)关于x轴对称的点的坐标为(﹣3,﹣2).
故选:D.
4.一个三角形的两边长分别为3和7,且第三边的边长为整数,这样的三角形的周长的最小值是( )
A.14 B.15 C.16 D.17
【分析】本题要先确定三角形的第三条边的长度,根据三角形的三边关系的定理可以确定.
【解答】解:设第三边的长为x,则
7﹣3<x<7+3,
所以4<x<10.
又x为整数,
所以x可取5,6,7,8,9.
所以这个三角形的周长的最小值为15.
故选:B.
5.一个多边形的内角和是外角和的3倍,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
【分析】根据多边形的外角和是360°,以及多边形的内角和定理即可求解.
【解答】解:设多边形的边数是n,则
(n﹣2) 180=3×360,
解得:n=8.
故选:D.
6.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=28°,则∠A的度数为( )
A.34° B.36° C.38° D.40°
【分析】利用角平分线的性质定理的逆定理得到BD平分∠ABC,则∠EBD=∠CBD=28°,然后利用互余计算∠A的度数.
【解答】解:∵DE⊥AB,DC⊥BC,DE=DC,
∴BD平分∠ABC,
∴∠EBD=∠CBD=28°,
∴∠A=90°﹣∠ABC=90°﹣2×28°=34°.
故选:A.
7.下列说法中,错误的是( )
A.全等三角形对应边上的中线相等
B.一个锐角和斜边对应相等的两个直角三角形全等
C.到直线I的距离相等的两个点关于直线l对称
D.三角形的一条中线将三角形分成两个面积相等的三角形
【分析】根据全等三角形的性质和判定,轴对称的性质分析即可.
【解答】解:A、全等三角形对应边上的中线相等,说法正确,不符合题意;
B、有一个锐角和斜边对应相等的两个直角三角形全等,说法正确,不符合题意;
C、到直线l的距离相等的两个点不一定关于直线l对称,说法错误,符合题意.
D、三角形的一条中线将三角形分成两个面积相等的三角形,说法正确,不符合题意.
故选:C.
8.如图,在五边形ABCDE中,若∠E=120°,则∠1+∠2+∠3+∠4的度数为( )
A.280° B.300° C.320° D.340°
【分析】多边形的外角和等于360°,由此即可计算.
【解答】解:∵∠E=120°,
∴∠E的外角是180°﹣120°=60°,
∵多边形的外角和等于360°,
∴∠1+∠2+∠3+∠4=360°﹣60°=300°.
故选:B.
9.如图,△ABC和△ADE关于直线l对称,连接BE,CD,CE,下列结论:
①l垂直平分CE;
②∠BAE=∠DAC;
③△BCE≌△DEC;
④直线BC,DE的交点一定在l上,
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据成轴对称的两个图形能够完全重合可得△ABC和△ADE全等,然后对各小题分析判断后解可得到答案.
【解答】解:∵△ABC和△ADE关于直线L对称,
∴①l垂直平分CE;
②∠BAE=∠DAC;
③△BCE≌△DEC;
④直线BC,DE的交点一定在l上,
综上所述,正确的结论有4个,
故选:D.
10.有一张三角形纸片ABC,已知∠B=∠C=α,按下列方案用剪刀沿着箭头方向剪开,所剪下的三角形纸片不一定是全等图形的是( )
A. B.
C. D.
【分析】根据全等三角形的判定定理进行判断即可.
【解答】解:A、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
B、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
C、如图1,
∵∠DEC=∠B+∠BDE=α+∠FEC,∠B=∠C=α,
∴∠FEC=∠BDE,
∵BD=CE=3是对应边,
由AAS判定两个小三角形全等
故本选项不符合题意;
D、如图2,
∵∠DEC=∠B+∠BDE=α+∠FEC,∠B=∠C=α,
∴∠FEC=∠BDE,
所以其对应边应该是BE和CF,而已知给的是BD=FC=3,
所以不能判定两个小三角形全等,故本选项符合题意;
故选:D.
二、填空题(本题共8小题,每小题3分,满分24分)
11.从六边形的一个顶点出发可以画出的对角线的条数是 3 .
【分析】根据从一个n边形一个顶点出发,可以连的对角线的条数是(n﹣3)进行计算即可.
【解答】解:从六边形的一个顶点出发,引对角线的数量为:6﹣3=3(条),
故答案为:3.
12.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是 ∠B=∠E或∠C=∠D或AB=AE .(只需写出一个条件即可)
【分析】利用∠1=∠2得到∠BAC=∠EAD,由于AC=AD,然后根据全等三角形的判定方法添加条件.
【解答】解:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即∠BAC=∠EAD,
∵AC=AD,
∴当添加∠B=∠E时,可根据“AAS”判断△ABC≌△AED;
当添加∠C=∠D时,可根据“ASA”判断△ABC≌△AED;
当添加AB=AE时,可根据“SAS”判断△ABC≌△AED.
故答案为∠B=∠E或∠C=∠D或AB=AE.
13.小明照镜子时,发现衣服上的英文单词在镜子中呈现为“”,则这个英文单词是 APPLE .
【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好左右颠倒,且关于镜面对称,分析并作答.
【解答】解:根据镜面对称的性质,分析可得题中所给的图片与成轴对称.
故答案为:APPLE.
14.如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系是 平行 .
【分析】根据全等三角形的判定与性质,可得∠A与∠C的关系,根据平行线的性质,可得答案.
【解答】解:在△AOD和△COB中,
,
∴△AOD≌△COB(SAS),
∴∠A=∠C.
∵∠A=∠C,
∴AD∥BC(内错角相等,两直线平行).
15.已知点A(a+1,2)关于y轴的对称点为B(3,b﹣1),则a+b的值为 ﹣5 .
【分析】直接利用关于y轴对称点的性质得出a,b的值,进而得出答案.
【解答】解:∵点A(a+1,2)关于y轴的对称点为B(3,b﹣1),
∴a+1=﹣3,b﹣1=﹣2,
解得:a=﹣4,b=﹣1,
∴a+b的值为:﹣4﹣1=﹣5.
故答案为:﹣5.
16.如图,在△ABC中,AB的垂直平分线交AB于点E,交边AC于点D,若BC=6cm,△BCD
的周长为14cm,则AC的长为 8cm .
【分析】根据线段的垂直平分线的性质得到DA=DB,再根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是AB的垂直平分线,
∴DA=DB,
∵△BCD的周长为14cm,
∴BC+CD+BD=14cm,
∴BC+CD+DA=BC+AC=14cm,
∵BC=6cm,
∴AC=8cm,
故答案为:8cm.
17.如图,将△ABC沿DE折叠,使点A落在点A'处,且BA'平分∠ABC,CA'平分∠ACB,若∠BA′C=110°,则∠1+∠2的度数为 80° .
【分析】连接A'A,先求出∠BAC,再证明∠1+∠2=2∠BAC即可解决问题.
【解答】解:如图,连接AA',
∵A'B平分∠ABC,A'C平分∠ACB,
∴∠A'BC=∠ABC,∠A'CB=∠ACB,
∵∠BA'C=110°,
∴∠A'BC+∠A'CB=180°﹣110°=70°,
∴∠ABC+∠ACB=140°,
∴∠BAC=180°﹣140°=40°,
∵沿DE折叠,
∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,
∵∠1=∠DAA'+∠DA'A=2∠DAA',∠2=∠EAA'+∠EA'A=2∠EAA',
∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×40°=80°,
故答案为:80°.
18.如图,在平面直角坐标系中,已知点A的坐标为(4,3).
①若△ABC是关于直线y=1的轴对称图形,则点B的坐标为 (4,﹣1) ;
②若△ABC是关于直线y=a的轴对称图形,则点B的坐标为 (4,2a﹣3) .
【分析】根据轴对称的性质,可得对称点的连线被对称轴垂直平分,即可得到两点到对称轴的距离相等.利用此性质可在坐标系中得到对应点的坐标.
【解答】解:根据题意,点A和点B是关于直线y=1对称的对应点,
∴它们到y=1的距离相等,是2个单位长度,AB⊥x轴,
∴点B的坐标是(4,﹣1).
若△ABC是关于直线y=a的轴对称图形,则点B的横坐标为4,纵坐标为a﹣(3﹣a)=2a﹣3,
∴点B的坐标为(4,2a﹣3),
故答案为:(4,﹣1),(4,2a﹣3).
三、计算与解答(本大题共46分)
19.(6分)如图,在4×4的方格中,请分别在甲、乙、丙三个图中添加一个正方形到空白方格中,与其余五个正方形组成的新图形是一个轴对称图形.
【分析】直接利用轴对称图形的性质得出符合题意的答案.
【解答】解:如图所示:
.
20.(8分)如图,在△ABC中,已知AD是角平分线,∠B=70°,∠C=40°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
【分析】(1)先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的性质求出∠BAD的度数,根据三角形内角和定理即可得出结论;
(2)根据三角形内角和定理即可得出结论.
【解答】解:(1)在△ABC中,∠B=70°,∠C=40°,
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣∠B﹣∠C=70°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=35°
在△ABD中,∠B=70°,∠BAD=35°,
∴∠ADB=180°﹣∠B﹣∠BAD=75°.
(2)∵∠CAD=∠BAC=35°,
又∵DE⊥AC,
∴在Rt△ADE中,∠EAD=35°,
∴∠ADE=90°﹣∠EAD=55°.
21.(8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE并延
长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AD=2,AB=5,当BC的长为 3 时,点B在线段AF的垂直平分线上.
【分析】(1)根据平行线的性质可得出∠DAE=∠CFE,结合E为CD的中点及对顶角相等,即可证出△ADE≌△FCE(AAS);
(2)根据等腰三角形的三线合一可得出BA=BF,由AB=6,AD=2,结合BC=BF﹣CF即可求出结论.
【解答】(1)证明:∵AD∥BC,即AD∥CF,
∴∠DAE=∠CFE.
∵E为CD的中点,
∴DE=CE.
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS).
(2)解:∵点B在线段AF的垂直平分线上,
∴BA=BF.
∵AB=5,AD=2,
∴BC=BF﹣CF=BA﹣DA=3.
故答案为:3.
22.(10分)如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点)和直线l.
(1)在直线l上找一点P,使点P到边AB,BC的距离相等;
(2)画出OABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位长度,画出平移后得到的图形△A2B2C2;
(3)结合轴对称变换和平移变换的有关性质,两个对应图形△ABC和△A2B2C2的对应点所具有的性质是 C .
A.对应点连线互相平行
B.对应点连线被直线l垂直平分
C.对应点连线被直线l平分或与直线l重合
【分析】(1)作∠ABC的平分线交l于点P;
(2)利用对称的性质和平移的性质画出△A1B1C1和△A2B2C2;
(3)利用AA2和BB2被l平分,CC2在直线l上可对各选项进行判断.
【解答】解:(1)如图,点P为所作;
(2)如图,△A1B1C1和△A2B2C2为所作;
(3)对应点连线被对称轴平分或与对称轴重合.
故选:C.
23.(14分)如图,CD是经过∠ACB顶点C的一条直线,AC=CB,E,F分别是直线CD.上两点,且∠AEC=∠CFB=α.
[数学思考]
(1)若直线CD经过∠ACB的内部,且E,F在射线CD上.
请解决下面两个问题:
①如图1,若∠ACB=90°,∠α=90°,则AE = CF,EF = AE﹣BF;(填“>”、“=”或“<”)
②如图2,若0°<∠ACB<90°,当∠ACB与α之间满足 ∠α+∠BCA=180° 时,能够使得①中的两个结论仍然成立,并证明两个结论.
[问题拓展]
(2)如图3,若直线CD经过∠ACB的外部,∠ACB=α,请提出EF,AE,BF三条线段数量关系的合理猜想(不要证明).
【分析】(1)①根据△ACE≌△CBF即可得到AE=CF,CE=BF,故EF=CF﹣CE=AE﹣BF;
②证明和(1)类似,根据△ACE≌△CBF即可得到AE=CF,CE=BF,故EF=CF﹣CE=AE﹣BF;
(2)求出∠AEC=∠BFC,∠CAE=∠BCF,根据AAS证△ACE≌△CBF,推出AE=CF,CE=BF即可.
【解答】解:(1)①∵∠BCA=∠AEC=∠BFC=90°,
∴∠ACE+∠BCF=90°,∠BCF+∠CBF=90°,
∴∠ACE=∠CBF,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∴EF=CF﹣CE=AE﹣BF,
故答案为=,=.
②在图2中,添加的条件为∠α+∠BCA=180°,
∴∠CFB+∠BCA=180°,
∴∠CFB+∠ACE+∠BCF=180°,
∵∠CFB+∠BCF+∠CBF=180°,
∴∠ACE=∠CBF,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∴EF=CF﹣CE=AE﹣BF.
故答案为:∠α+∠BCA=180°;
(2)EF=AE+BF.
理由是:如图3中,
∵∠AEC=∠CFB=∠a,∠a=∠BCA,
又∵∠EAC+∠ACE+∠AEC=180°,∠ACE+∠BCF+∠ACB=180°,
∴∠EAC+∠ACE=∠ACE+∠BCF,
∴∠EAC=∠BCF,
在△AEC和△CFB中,
,
∴△AEC≌△CFB(AAS),
∴BF=CE,AE=CF,
∵EF=CE+CF,
∴EF=AE+BF.
一、选择题(本题共10小题,每小题3分,满分30分)下列各题的四个选项中,只有一个是正确的。
1.下列卡通动物简笔画图案中,属于轴对称图形的是( )
A. B.
C. D.
2.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为( )
A.120° B.80° C.60° D.40°
3.在平面直角坐标系xOy中,点M(﹣3,2)关于x轴对称的点的坐标是( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
4.一个三角形的两边长分别为3和7,且第三边的边长为整数,这样的三角形的周长的最小值是( )
A.14 B.15 C.16 D.17
5.一个多边形的内角和是外角和的3倍,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
6.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=28°,则∠A的度数为( )
A.34° B.36° C.38° D.40°
7.下列说法中,错误的是( )
A.全等三角形对应边上的中线相等
B.一个锐角和斜边对应相等的两个直角三角形全等
C.到直线I的距离相等的两个点关于直线l对称
D.三角形的一条中线将三角形分成两个面积相等的三角形
8.如图,在五边形ABCDE中,若∠E=120°,则∠1+∠2+∠3+∠4的度数为( )
A.280° B.300° C.320° D.340°
9.如图,△ABC和△ADE关于直线l对称,连接BE,CD,CE,下列结论:
①l垂直平分CE;
②∠BAE=∠DAC;
③△BCE≌△DEC;
④直线BC,DE的交点一定在l上,
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.有一张三角形纸片ABC,已知∠B=∠C=α,按下列方案用剪刀沿着箭头方向剪开,所剪下的三角形纸片不一定是全等图形的是( )
A. B.
C. D.
二、填空题(本题共8小题,每小题3分,满分24分)
11.从六边形的一个顶点出发可以画出的对角线的条数是 .
12.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是 .(只需写出一个条件即可)
13.小明照镜子时,发现衣服上的英文单词在镜子中呈现为“”,则这个英文单词是 .
14.如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系是 .
15.已知点A(a+1,2)关于y轴的对称点为B(3,b﹣1),则a+b的值为 .
16.如图,在△ABC中,AB的垂直平分线交AB于点E,交边AC于点D,若BC=6cm,△BCD
的周长为14cm,则AC的长为 .
17.如图,将△ABC沿DE折叠,使点A落在点A'处,且BA'平分∠ABC,CA'平分∠ACB,若∠BA′C=110°,则∠1+∠2的度数为 .
18.如图,在平面直角坐标系中,已知点A的坐标为(4,3).
①若△ABC是关于直线y=1的轴对称图形,则点B的坐标为 ;
②若△ABC是关于直线y=a的轴对称图形,则点B的坐标为 .
三、计算与解答(本大题共46分)
19.(6分)如图,在4×4的方格中,请分别在甲、乙、丙三个图中添加一个正方形到空白方格中,与其余五个正方形组成的新图形是一个轴对称图形.
20.(8分)如图,在△ABC中,已知AD是角平分线,∠B=70°,∠C=40°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
21.(8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE并延
长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AD=2,AB=5,当BC的长为 时,点B在线段AF的垂直平分线上.
22.(10分)如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点)和直线l.
(1)在直线l上找一点P,使点P到边AB,BC的距离相等;
(2)画出OABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位长度,画出平移后得到的图形△A2B2C2;
(3)结合轴对称变换和平移变换的有关性质,两个对应图形△ABC和△A2B2C2的对应点所具有的性质是 .
A.对应点连线互相平行
B.对应点连线被直线l垂直平分
C.对应点连线被直线l平分或与直线l重合
23.(14分)如图,CD是经过∠ACB顶点C的一条直线,AC=CB,E,F分别是直线CD.上两点,且∠AEC=∠CFB=α.
[数学思考]
(1)若直线CD经过∠ACB的内部,且E,F在射线CD上.
请解决下面两个问题:
①如图1,若∠ACB=90°,∠α=90°,则AE CF,EF AE﹣BF;(填“>”、“=”或“<”)
②如图2,若0°<∠ACB<90°,当∠ACB与α之间满足 时,能够使得①中的两个结论仍然成立,并证明两个结论.
[问题拓展]
(2)如图3,若直线CD经过∠ACB的外部,∠ACB=α,请提出EF,AE,BF三条线段数量关系的合理猜想(不要证明).
2022-2023学年安徽省淮南市谢家集区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题共10小题,每小题3分,满分30分)下列各题的四个选项中,只有一个是正确的。
1.下列卡通动物简笔画图案中,属于轴对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选:D.
2.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为( )
A.120° B.80° C.60° D.40°
【分析】直接用一个未知数表示出∠A,∠B,∠C的度数,再利用三角形内角和定理得出答案.
【解答】解:∵∠A:∠B:∠C=2:3:4,
∴设∠A=2x,∠B=3x,∠C=4x,
∵∠A+∠B+∠C=180°,
∴2x+3x+4x=180°,
解得:x=20°,
∴∠B的度数为:60°.
故选:C.
3.在平面直角坐标系xOy中,点M(﹣3,2)关于x轴对称的点的坐标是( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
【分析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答即可.
【解答】解:点M(﹣3,2)关于x轴对称的点的坐标为(﹣3,﹣2).
故选:D.
4.一个三角形的两边长分别为3和7,且第三边的边长为整数,这样的三角形的周长的最小值是( )
A.14 B.15 C.16 D.17
【分析】本题要先确定三角形的第三条边的长度,根据三角形的三边关系的定理可以确定.
【解答】解:设第三边的长为x,则
7﹣3<x<7+3,
所以4<x<10.
又x为整数,
所以x可取5,6,7,8,9.
所以这个三角形的周长的最小值为15.
故选:B.
5.一个多边形的内角和是外角和的3倍,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
【分析】根据多边形的外角和是360°,以及多边形的内角和定理即可求解.
【解答】解:设多边形的边数是n,则
(n﹣2) 180=3×360,
解得:n=8.
故选:D.
6.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=28°,则∠A的度数为( )
A.34° B.36° C.38° D.40°
【分析】利用角平分线的性质定理的逆定理得到BD平分∠ABC,则∠EBD=∠CBD=28°,然后利用互余计算∠A的度数.
【解答】解:∵DE⊥AB,DC⊥BC,DE=DC,
∴BD平分∠ABC,
∴∠EBD=∠CBD=28°,
∴∠A=90°﹣∠ABC=90°﹣2×28°=34°.
故选:A.
7.下列说法中,错误的是( )
A.全等三角形对应边上的中线相等
B.一个锐角和斜边对应相等的两个直角三角形全等
C.到直线I的距离相等的两个点关于直线l对称
D.三角形的一条中线将三角形分成两个面积相等的三角形
【分析】根据全等三角形的性质和判定,轴对称的性质分析即可.
【解答】解:A、全等三角形对应边上的中线相等,说法正确,不符合题意;
B、有一个锐角和斜边对应相等的两个直角三角形全等,说法正确,不符合题意;
C、到直线l的距离相等的两个点不一定关于直线l对称,说法错误,符合题意.
D、三角形的一条中线将三角形分成两个面积相等的三角形,说法正确,不符合题意.
故选:C.
8.如图,在五边形ABCDE中,若∠E=120°,则∠1+∠2+∠3+∠4的度数为( )
A.280° B.300° C.320° D.340°
【分析】多边形的外角和等于360°,由此即可计算.
【解答】解:∵∠E=120°,
∴∠E的外角是180°﹣120°=60°,
∵多边形的外角和等于360°,
∴∠1+∠2+∠3+∠4=360°﹣60°=300°.
故选:B.
9.如图,△ABC和△ADE关于直线l对称,连接BE,CD,CE,下列结论:
①l垂直平分CE;
②∠BAE=∠DAC;
③△BCE≌△DEC;
④直线BC,DE的交点一定在l上,
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据成轴对称的两个图形能够完全重合可得△ABC和△ADE全等,然后对各小题分析判断后解可得到答案.
【解答】解:∵△ABC和△ADE关于直线L对称,
∴①l垂直平分CE;
②∠BAE=∠DAC;
③△BCE≌△DEC;
④直线BC,DE的交点一定在l上,
综上所述,正确的结论有4个,
故选:D.
10.有一张三角形纸片ABC,已知∠B=∠C=α,按下列方案用剪刀沿着箭头方向剪开,所剪下的三角形纸片不一定是全等图形的是( )
A. B.
C. D.
【分析】根据全等三角形的判定定理进行判断即可.
【解答】解:A、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
B、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
C、如图1,
∵∠DEC=∠B+∠BDE=α+∠FEC,∠B=∠C=α,
∴∠FEC=∠BDE,
∵BD=CE=3是对应边,
由AAS判定两个小三角形全等
故本选项不符合题意;
D、如图2,
∵∠DEC=∠B+∠BDE=α+∠FEC,∠B=∠C=α,
∴∠FEC=∠BDE,
所以其对应边应该是BE和CF,而已知给的是BD=FC=3,
所以不能判定两个小三角形全等,故本选项符合题意;
故选:D.
二、填空题(本题共8小题,每小题3分,满分24分)
11.从六边形的一个顶点出发可以画出的对角线的条数是 3 .
【分析】根据从一个n边形一个顶点出发,可以连的对角线的条数是(n﹣3)进行计算即可.
【解答】解:从六边形的一个顶点出发,引对角线的数量为:6﹣3=3(条),
故答案为:3.
12.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是 ∠B=∠E或∠C=∠D或AB=AE .(只需写出一个条件即可)
【分析】利用∠1=∠2得到∠BAC=∠EAD,由于AC=AD,然后根据全等三角形的判定方法添加条件.
【解答】解:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即∠BAC=∠EAD,
∵AC=AD,
∴当添加∠B=∠E时,可根据“AAS”判断△ABC≌△AED;
当添加∠C=∠D时,可根据“ASA”判断△ABC≌△AED;
当添加AB=AE时,可根据“SAS”判断△ABC≌△AED.
故答案为∠B=∠E或∠C=∠D或AB=AE.
13.小明照镜子时,发现衣服上的英文单词在镜子中呈现为“”,则这个英文单词是 APPLE .
【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好左右颠倒,且关于镜面对称,分析并作答.
【解答】解:根据镜面对称的性质,分析可得题中所给的图片与成轴对称.
故答案为:APPLE.
14.如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系是 平行 .
【分析】根据全等三角形的判定与性质,可得∠A与∠C的关系,根据平行线的性质,可得答案.
【解答】解:在△AOD和△COB中,
,
∴△AOD≌△COB(SAS),
∴∠A=∠C.
∵∠A=∠C,
∴AD∥BC(内错角相等,两直线平行).
15.已知点A(a+1,2)关于y轴的对称点为B(3,b﹣1),则a+b的值为 ﹣5 .
【分析】直接利用关于y轴对称点的性质得出a,b的值,进而得出答案.
【解答】解:∵点A(a+1,2)关于y轴的对称点为B(3,b﹣1),
∴a+1=﹣3,b﹣1=﹣2,
解得:a=﹣4,b=﹣1,
∴a+b的值为:﹣4﹣1=﹣5.
故答案为:﹣5.
16.如图,在△ABC中,AB的垂直平分线交AB于点E,交边AC于点D,若BC=6cm,△BCD
的周长为14cm,则AC的长为 8cm .
【分析】根据线段的垂直平分线的性质得到DA=DB,再根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是AB的垂直平分线,
∴DA=DB,
∵△BCD的周长为14cm,
∴BC+CD+BD=14cm,
∴BC+CD+DA=BC+AC=14cm,
∵BC=6cm,
∴AC=8cm,
故答案为:8cm.
17.如图,将△ABC沿DE折叠,使点A落在点A'处,且BA'平分∠ABC,CA'平分∠ACB,若∠BA′C=110°,则∠1+∠2的度数为 80° .
【分析】连接A'A,先求出∠BAC,再证明∠1+∠2=2∠BAC即可解决问题.
【解答】解:如图,连接AA',
∵A'B平分∠ABC,A'C平分∠ACB,
∴∠A'BC=∠ABC,∠A'CB=∠ACB,
∵∠BA'C=110°,
∴∠A'BC+∠A'CB=180°﹣110°=70°,
∴∠ABC+∠ACB=140°,
∴∠BAC=180°﹣140°=40°,
∵沿DE折叠,
∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,
∵∠1=∠DAA'+∠DA'A=2∠DAA',∠2=∠EAA'+∠EA'A=2∠EAA',
∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×40°=80°,
故答案为:80°.
18.如图,在平面直角坐标系中,已知点A的坐标为(4,3).
①若△ABC是关于直线y=1的轴对称图形,则点B的坐标为 (4,﹣1) ;
②若△ABC是关于直线y=a的轴对称图形,则点B的坐标为 (4,2a﹣3) .
【分析】根据轴对称的性质,可得对称点的连线被对称轴垂直平分,即可得到两点到对称轴的距离相等.利用此性质可在坐标系中得到对应点的坐标.
【解答】解:根据题意,点A和点B是关于直线y=1对称的对应点,
∴它们到y=1的距离相等,是2个单位长度,AB⊥x轴,
∴点B的坐标是(4,﹣1).
若△ABC是关于直线y=a的轴对称图形,则点B的横坐标为4,纵坐标为a﹣(3﹣a)=2a﹣3,
∴点B的坐标为(4,2a﹣3),
故答案为:(4,﹣1),(4,2a﹣3).
三、计算与解答(本大题共46分)
19.(6分)如图,在4×4的方格中,请分别在甲、乙、丙三个图中添加一个正方形到空白方格中,与其余五个正方形组成的新图形是一个轴对称图形.
【分析】直接利用轴对称图形的性质得出符合题意的答案.
【解答】解:如图所示:
.
20.(8分)如图,在△ABC中,已知AD是角平分线,∠B=70°,∠C=40°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
【分析】(1)先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的性质求出∠BAD的度数,根据三角形内角和定理即可得出结论;
(2)根据三角形内角和定理即可得出结论.
【解答】解:(1)在△ABC中,∠B=70°,∠C=40°,
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣∠B﹣∠C=70°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=35°
在△ABD中,∠B=70°,∠BAD=35°,
∴∠ADB=180°﹣∠B﹣∠BAD=75°.
(2)∵∠CAD=∠BAC=35°,
又∵DE⊥AC,
∴在Rt△ADE中,∠EAD=35°,
∴∠ADE=90°﹣∠EAD=55°.
21.(8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE并延
长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AD=2,AB=5,当BC的长为 3 时,点B在线段AF的垂直平分线上.
【分析】(1)根据平行线的性质可得出∠DAE=∠CFE,结合E为CD的中点及对顶角相等,即可证出△ADE≌△FCE(AAS);
(2)根据等腰三角形的三线合一可得出BA=BF,由AB=6,AD=2,结合BC=BF﹣CF即可求出结论.
【解答】(1)证明:∵AD∥BC,即AD∥CF,
∴∠DAE=∠CFE.
∵E为CD的中点,
∴DE=CE.
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS).
(2)解:∵点B在线段AF的垂直平分线上,
∴BA=BF.
∵AB=5,AD=2,
∴BC=BF﹣CF=BA﹣DA=3.
故答案为:3.
22.(10分)如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点)和直线l.
(1)在直线l上找一点P,使点P到边AB,BC的距离相等;
(2)画出OABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位长度,画出平移后得到的图形△A2B2C2;
(3)结合轴对称变换和平移变换的有关性质,两个对应图形△ABC和△A2B2C2的对应点所具有的性质是 C .
A.对应点连线互相平行
B.对应点连线被直线l垂直平分
C.对应点连线被直线l平分或与直线l重合
【分析】(1)作∠ABC的平分线交l于点P;
(2)利用对称的性质和平移的性质画出△A1B1C1和△A2B2C2;
(3)利用AA2和BB2被l平分,CC2在直线l上可对各选项进行判断.
【解答】解:(1)如图,点P为所作;
(2)如图,△A1B1C1和△A2B2C2为所作;
(3)对应点连线被对称轴平分或与对称轴重合.
故选:C.
23.(14分)如图,CD是经过∠ACB顶点C的一条直线,AC=CB,E,F分别是直线CD.上两点,且∠AEC=∠CFB=α.
[数学思考]
(1)若直线CD经过∠ACB的内部,且E,F在射线CD上.
请解决下面两个问题:
①如图1,若∠ACB=90°,∠α=90°,则AE = CF,EF = AE﹣BF;(填“>”、“=”或“<”)
②如图2,若0°<∠ACB<90°,当∠ACB与α之间满足 ∠α+∠BCA=180° 时,能够使得①中的两个结论仍然成立,并证明两个结论.
[问题拓展]
(2)如图3,若直线CD经过∠ACB的外部,∠ACB=α,请提出EF,AE,BF三条线段数量关系的合理猜想(不要证明).
【分析】(1)①根据△ACE≌△CBF即可得到AE=CF,CE=BF,故EF=CF﹣CE=AE﹣BF;
②证明和(1)类似,根据△ACE≌△CBF即可得到AE=CF,CE=BF,故EF=CF﹣CE=AE﹣BF;
(2)求出∠AEC=∠BFC,∠CAE=∠BCF,根据AAS证△ACE≌△CBF,推出AE=CF,CE=BF即可.
【解答】解:(1)①∵∠BCA=∠AEC=∠BFC=90°,
∴∠ACE+∠BCF=90°,∠BCF+∠CBF=90°,
∴∠ACE=∠CBF,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∴EF=CF﹣CE=AE﹣BF,
故答案为=,=.
②在图2中,添加的条件为∠α+∠BCA=180°,
∴∠CFB+∠BCA=180°,
∴∠CFB+∠ACE+∠BCF=180°,
∵∠CFB+∠BCF+∠CBF=180°,
∴∠ACE=∠CBF,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∴EF=CF﹣CE=AE﹣BF.
故答案为:∠α+∠BCA=180°;
(2)EF=AE+BF.
理由是:如图3中,
∵∠AEC=∠CFB=∠a,∠a=∠BCA,
又∵∠EAC+∠ACE+∠AEC=180°,∠ACE+∠BCF+∠ACB=180°,
∴∠EAC+∠ACE=∠ACE+∠BCF,
∴∠EAC=∠BCF,
在△AEC和△CFB中,
,
∴△AEC≌△CFB(AAS),
∴BF=CE,AE=CF,
∵EF=CE+CF,
∴EF=AE+BF.
同课章节目录
