3.1.1图形的平移

3.1.1《图形的平移》
课时：第 课时 主备人：朱振宏 复核人：
学习重点：探究平移变换的基本要素，画简单图形的平移图
学习过程：
一.自主预习
1.平移: 。
平移不改变图形的____________________,只改变图形的 .
2.连接各组对应点的线段______且________或_______。对应线段_____且______或_______；
对应角:_______。
3.决定平移的要素： ；平移的方向： ；平移的距离： 。
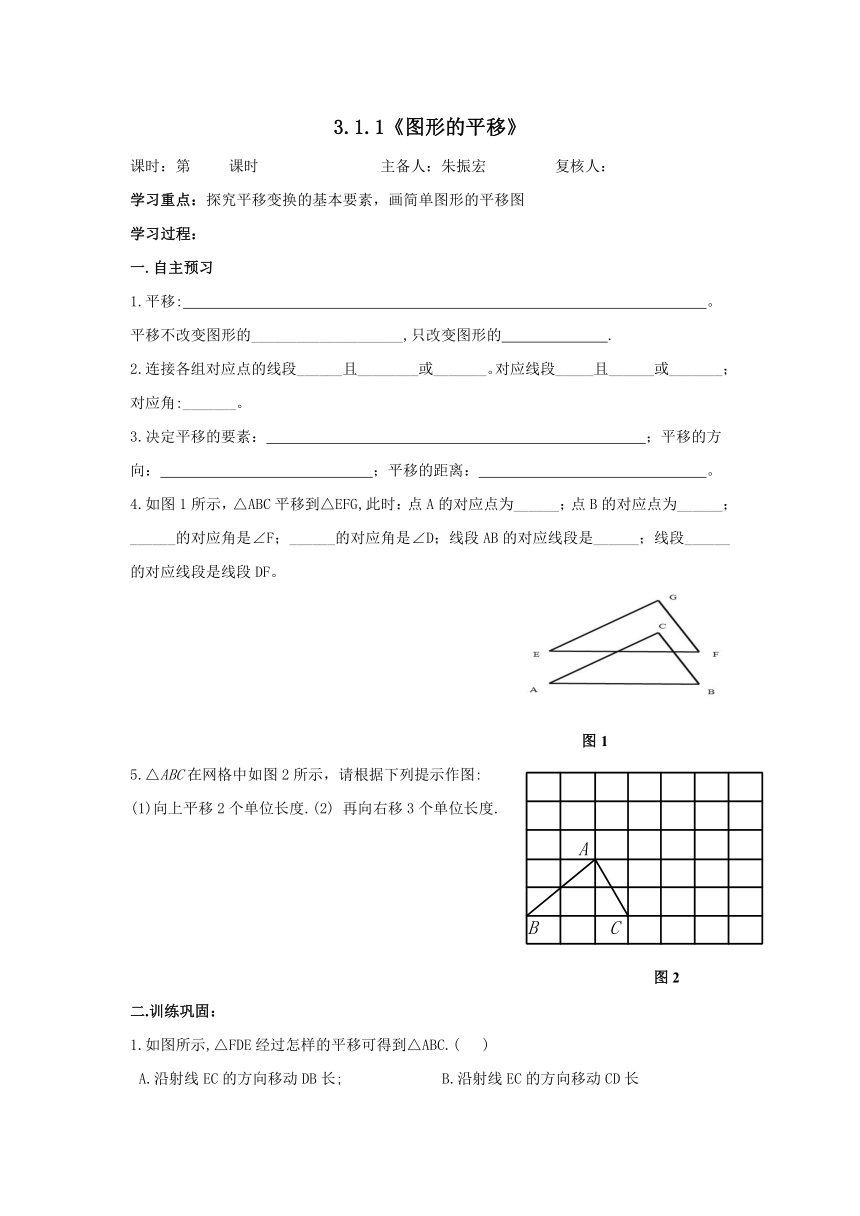
4.如图1所示，△ABC平移到△EFG,此时：点A的对应点为______；点B的对应点为______；______的对应角是∠F；______的对应角是∠D；线段AB的对应线段是______；线段______的对应线段是线段DF。
图1
5.△ABC在网格中如图2所示，请根据下列提示作图:
(1)向上平移2个单位长度.(2) 再向右移3个单位长度.
图2
二.训练巩固：
1.如图所示,△FDE经过怎样的平移可得到△ABC.( )
A.沿射线EC的方向移动DB长; B.沿射线EC的方向移动CD长
C.沿射线BD的方向移动BD长; D.沿射线BD的方向移动DC长
2.下列四组图形中,有一组中的两个图形经过平移其中一个能得到 另一个,这组图形是( )
3.如图3所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是( )
A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC
4.在平移过程中,对应线段( )
A.互相平行且相等; B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等 图3
5.将直角边为3cm,4cm的直角三角形ABC向左平移4cm,得到Rt△A′B′C′,则△A′B′C′是______ 三角形，它的边长分别为_____,_____,_____,面积为_____。
三.拓展延伸：
1.将字母A按箭头所指的方向平移3厘米，作出平移后的图形。
2.如图11-7，某宾馆在重新装修后考虑在大厅内的主楼梯上铺设地毯，已知主楼梯梯宽3米，其剖面如图11－7所不，请你计算一下：（1）仅此楼梯，需要购买地毯多少米？（2）购买地毯多少平方米？
3.如图，已知Rt△ABC中，∠C=90°，BC=4，AC=4，现将△ABC沿CB方向平移到△A’B’C’的位置。
（1）若平移距离为3，求△ABC与△A’B’C’的重叠部分的面积；
（2）若平移距离为x（ ），求△ABC与△A’B’C’的重叠部分的面积y，并写出y与x的关系式。
四、分层作业：
E
C
B
A
D