高中数学必修四第二章:平面向量精美导学案(共计28页)
文档属性
| 名称 | 高中数学必修四第二章:平面向量精美导学案(共计28页) |  | |
| 格式 | zip | ||
| 文件大小 | 335.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-29 15:29:10 | ||
图片预览



文档简介
第二章 平面向量
2.1 向量的概念及表示
【学习目标】
1.了解向量的实际背景,理解平面向量的概念和向量的几何表示;掌握向量的模、零向量、单位向量、平行向量、相等向量、共线向量的概念;并会区分平行向量、相等向量和共线向量;
2.通过对向量的学习,使学生初步认识现实生活中的向量和数量的本质区别;
3.通过学生对向量与数量的识别能力的训练,培养学生认识客观事物的数学本质的能力。
【学习重难点】
重点:平行向量的概念和向量的几何表示;
难点:区分平行向量、相等向量和共线向量;
【自主学习】
1.向量的定义:__________________________________________________________;
2.向量的表示:
(1)图形表示:
(2)字母表示:
3.向量的相关概念:
(1)向量的长度(向量的模):_______________________记作:______________
(2)零向量:___________________,记作:_____________________
(3)单位向量:________________________________
(4)平行向量:________________________________
(5)共线向量:________________________________
(6)相等向量与相反向量:_________________________
思考:
(1)平面直角坐标系中,起点是原点的单位向量,它们的终点的轨迹是什么图形?____
(2)平行向量与共线向量的关系:____________________________________________
(3)向量“共线”与几何中“共线”有何区别:__________________________________
【典型例题】
例1.判断下例说法是否正确,若不正确请改正:
(1)零向量是唯一没有方向的向量;
(2)平面内的向量单位只有一个;
(3)方向相反的向量是共线向量,共线向量不一定是相反向量;
(4)向量和是共线向量,,则和是方向相同的向量;
(5)相等向量一定是共线向量;
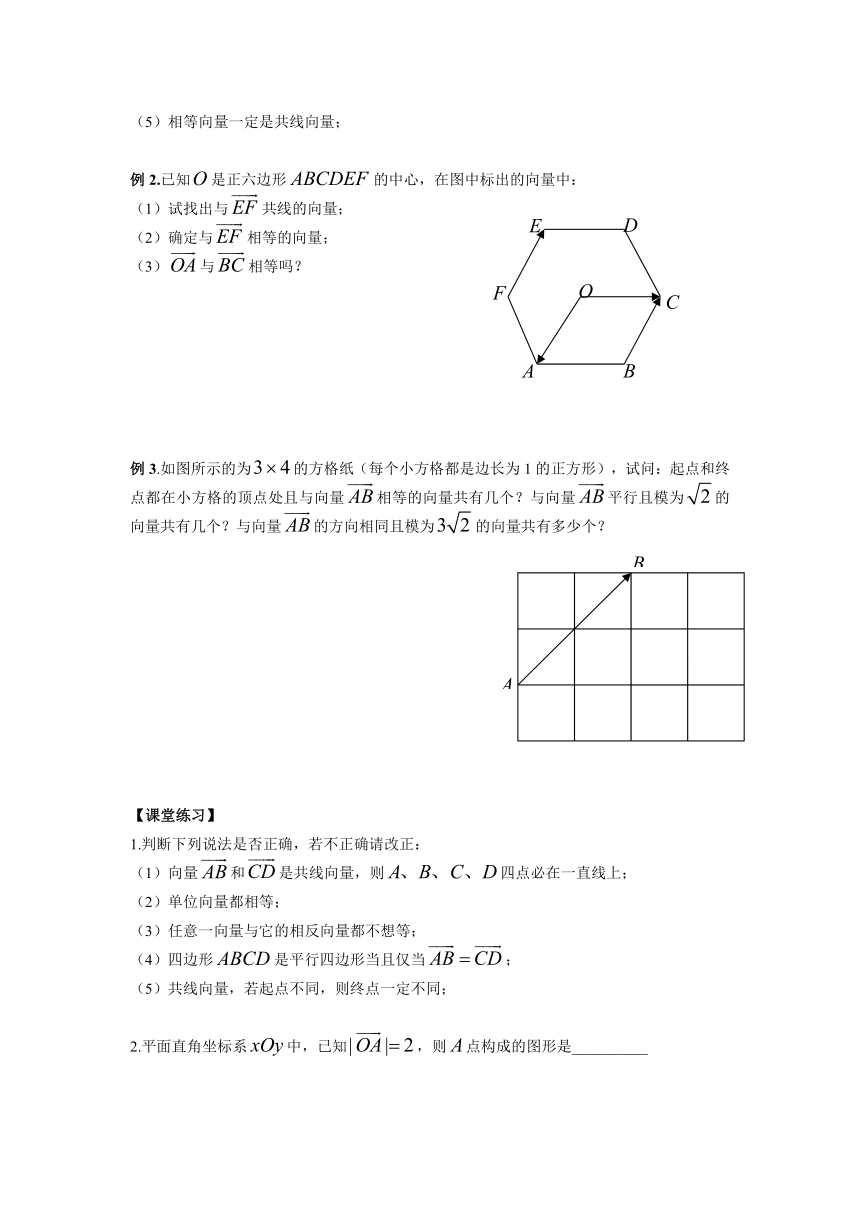
例2.已知是正六边形的中心,在图中标出的向量中:
(1)试找出与共线的向量;
(2)确定与相等的向量;
(3)与相等吗?
例3.如图所示的为的方格纸(每个小方格都是边长为1的正方形),试问:起点和终点都在小方格的顶点处且与向量相等的向量共有几个?与向量平行且模为的向量共有几个?与向量的方向相同且模为的向量共有多少个?
【课堂练习】
1.判断下列说法是否正确,若不正确请改正:
(1)向量和是共线向量,则四点必在一直线上;
(2)单位向量都相等;
(3)任意一向量与它的相反向量都不想等;
(4)四边形是平行四边形当且仅当;
(5)共线向量,若起点不同,则终点一定不同;
2.平面直角坐标系中,已知,则点构成的图形是__________
3.四边形中,,则四边形的形状是_________
4.设,则与方向相同的单位向量是______________
5.若分别是四边形的边的中点。
求证:
6.已知飞机从甲地北偏东的方向飞行到达乙地,再从乙地按南偏东的方向飞行到达丙地,再从丙地按西南方向飞行到达丁地,问:丁地在甲地的什么方向?丁地距甲地多远?
【课堂小结】
(编者:尹欣)
2.2.1 向量的加法
【学习目标】
1.掌握向量加法的定义;
2.会用向量加法的三角法则和向量的平行四边形法则作两个向量的和向量;
3.掌握向量加法的交换律和结合律,并会用它们进行向量计算
【学习重难点】
重点:向量加法的三角法则、平行四边形则和加法运算律;
难点:向量加法的三角法则、平行四边形则和加法运算律;
【自主学习】
1.向量的和、向量的加法:
已知向量和,______________________________________________________
则向量叫做与的和,记作:____________________________________
_________________________________叫做向量的加法
注意:两个向量的和向量还是一个向量;
2.向量加法的几何作法:
(1)三角形法则的步骤:
①
②
③
就是所做的
(2)平行四边形法则的步骤:
①
②
③
就是所做的
注意:向量加法的平行四边形法则,只适用于对两个不共线的向量相加,而向量加法的三角形法则对于任何两个向量都适用。
3.向量加法的运算律:
(1)向量加法的交换律:
_________________________________________
(2)向量加法的结合律:
_________________________________________
思考:如果平面内有个向量依次首尾相接组成一条封闭折线,那么这条向量的和是什么?________________
【例题讲解】
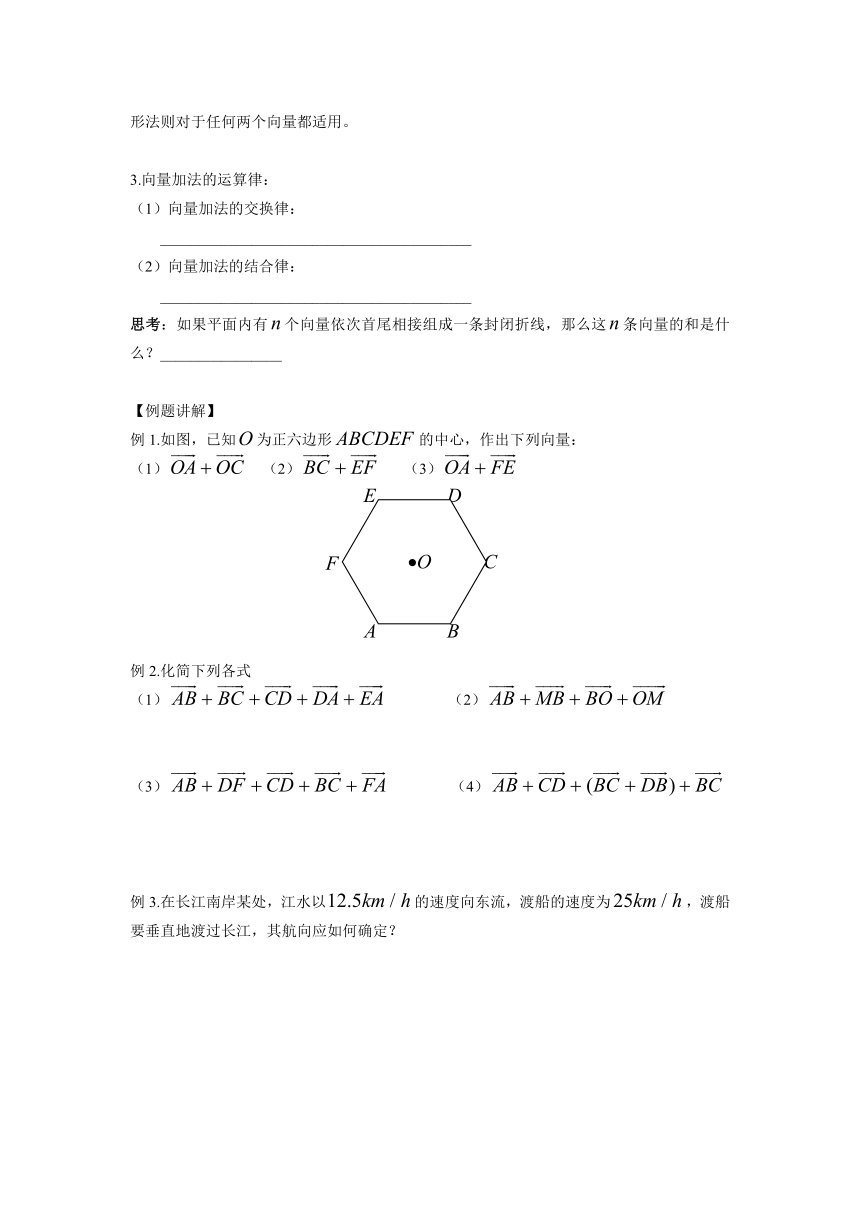
例1.如图,已知为正六边形的中心,作出下列向量:
(1) (2) (3)
例2.化简下列各式
(1) (2)
(3) (4)
例3.在长江南岸某处,江水以的速度向东流,渡船的速度为,渡船要垂直地渡过长江,其航向应如何确定?
【课堂练习】
1.已知,求作:
(1)
(2)
2.已知是平行四边形的交点,下列结论正确的有_________
(1) (2)
(3) (4)
3.设点是内一点,若,则点为的______心;
4.对于任意的,不等式成立吗?请说明理由。
【课堂小结】
(编者:尹欣)
2.2.2 向量的减法
【学习目标】
1.理解向量减法的概念;
2.会做两个向量的差;
3.会进行向量加、减得混合运算
4.培养学生的辩证思维能力和认识问题的能力
【学习重难点】
重点:三角形法则
难点:三角形法则,向量加、减混合运算
【自主学习】
1.向量的减法:
①与的差:若__________________,则向量叫做与的差,记为__________
②向量与的减法:求两个向量差的运算叫做向量的减法;
注意:向量的减法是向量加法的逆运算。
2.向量的减法的作图方法:
作法:①_______________________________
②________________________________
③________________________________
则
3.减去一个向量等于加上这个向量的相反向量
4.关于向量减法需要注意一下几点:
①在用三角形法则做向量减法时,只要记住连接两向量的终点,箭头指向被减向量即可.
②以向量为邻边作平行四边形,则两条对角线的向量为,这一结论在以后应用还是非常广泛,应加强理解;
③对于任意一点,,简记“终减起”,在解题中经常用到,必须记住.
【例题讲解】
例1.已知向量,求作向量:;
思考:如果,怎么做出?
例2.已知是平行四边形的对角线的交点,若试证明:
本题还可以考虑如下方法:
1.(1)
(2)
2.任意一个非零向量都可以表示为两个不共线的向量和。
例3.化简下列各式
(1)
(2)
(3)
【课堂练习】
1.在中,,,下列等式成立的有_____________
(1)
(2)
(3)
(4)
2.已知四边形的对角线与相交与点,且,
求证:四边形是平行四边形。
3.如图,是一个梯形,,分别是的中点,已知试用表示和
【课堂小结】
(编者:尹欣)
2.2.3 向量的数乘(1)
【学习目标】
1.掌握向量数乘的定义,会确定向量数乘后的方向和模;
2.掌握向量数乘的运算律,并会用它进行计算;
3.通过本课的学习,渗透类比思想和化归思想
【学习重难点】
重点:向量的数乘及运算律;
难点:向量的数乘及运算律;
【自主学习】
1.向量的数乘的定义:
一般地,实数与向量的积是一个向量,记作:_______;它的长度和方向规定如下:
(1)
(2)当时,_______________________;
当时,_______________________;
当时,_______________________;
______________________________叫做向量的数乘
2.向量的线性运算定义:
___________________________________________统称为向量的线性运算;
3.向量的数乘的作图:
已知作
当时,把按原来的方向变为原来的倍;
当时,把按原来的相反方向变为原来的倍;
4.向量的数乘满足的运算律:
设为任意实数,为任意向量,则
(1)结合律
______________________________________
(2)分配律
_______________________________________
注意:(1)向量本身具有“形”和“数”的双重特点,而在实数与向量的积得运算过程中,既要考虑模的大小,又要考虑方向,因此它是数形结合的具体应用,这一点提示我们研究向量不能脱离它的几何意义;
(2)向量的数乘及运算性质可类比整式的乘法来理解和记忆。
【典型例题】
例1.已知向量,求作:
(1)向量
(2)
例2.计算
(1)
(2)
(3)
注意:(1)向量的数乘与实数的数乘的区别:相同点:这两种运算都满足结合律和分配律。不同点:实数的数乘的结果(积)是一个实数,而向量的数乘的结果是一个向量。
(2)向量的线性运算的结果是一个向量,运算法则与多项式运算类似。
例3.已知是不共线的向量,,试用表示
例4.已知:中,为的中点,为的中点,相交于点,求证:
(1)
(2)
(3)
【课堂练习】
1.计算:
(1)
(2)
2.已知向量且求
3.在平行四边形中,为的中点,用来表示
4.如图,在中,为边的中线,为的重心,求向量
【课堂小结】
(编者:尹欣)
2.2.3 向量的数乘(2)
【学习目标】
1.理解并掌握向量的共线定理;
2.能运用向量共线定理证明简单的几何问题;
3.培养学生的逻辑思维能力
【学习重难点】
重点:向量的共线定理;
难点:向量的共线定理;
【自主学习】
1.向量的线性表示:
若果,则称向量可以用非零向量线性表示;
2.向量共线定理:
思考:向量共线定理中有这个限制条件,若无此条件,会有什么结果?
【典型例题】
例1.如图,分别是的边的中点,
(1)将用线性表示;
(2)求证:与共线;
例2.设是两个不共线的向量,已知,若三点共线,求的值。
变式:设是两个不共线的向量,已知
,求证:三点共线。
例3.如图,中,为直线上一点,
求证:
思考:
(1)当时,你能得到什么结论?
(2)上面所证的结论:表明:起点为,终点为直线上一点的向量可以用表示,那么两个不共线的向量可以表示平面上任意一个向量吗?
例4.已知向量其中不共线,向量,是否存在实数,使得与共线
例5.平面直角坐标系中,已知若点满足其中三点共线,求的值;
【课堂练习】
1.已知向量求证:为共线向量;
2.设是两个不共线的向量,若是共线向量,求的值。
3.求证:起点相同的三个非零向量的终点在同一直线上。
【课堂小结】
(编者:尹欣)
2.3.1 平面向量基本原理
【学习目标】
了解平面向量的基本定理及其意义;
掌握三点(或三点以上)的共线的证明方法:
提高学生分析问题、解决问题的能力。
【预习指导】
1、平面向量的基本定理
如果,是同一平面内两个不共线的向量,那么对于这一平面内的任一向量,有且只有一对实数,使=+
2.、基底:
平面向量的基本定理中的不共线的向量, ,称为这一平面内所有向量的一组基底。
思考:
向量作为基底必须具备什么条件?
一个平面的基底唯一吗?
答:(1)______________________________________________________
(2)______________________________________________________
3、向量的分解、向量的正交分解:
一个平面向量用一组基底 , 表示成=+的形式,我们称它为向量的分解,当, 互相垂直时,就称为向量的正交分解。
点共线的证明方法:___________________________________________
【典例选讲】
例1:如图:平行四边形ABCD的对角线AC和BD交于一点M , = , =试用 ,,表示 , , 和 。
D C
M
A B
例2: 设 , 是平面的一组基底,如果 =3 —2 , =4 + ,=8 —9,求证:A、B、D三点共线。
例3: 如图,在平行四边形ABCD中,点 M在 AB的延长线上,且 BM=AB,点N 在 BC上,且BN=BC ,用向量法证明: M、N、D 三点共线。
D C
N
A B M
【课堂练习】
1、若,是平面内所有向量的一组基底,则下面的四组向量中不能作为一组基底的( )
A、 —2 和+2
B 、与3
C、2+3和 - 4—6
D、+与
2、若,是平面内所有向量的一组基底,那么下列结论成立的是( )
A、若实数,使+=0,则==0
B、空间任意向量都可以表示为=+,,R
C、+,,R不一定表示平面内一个向量
D、对于这一平面内的任一向量 ,使=+的实数对,有无数对
3、三角形ABC中,若 D,E,F 依次是 四等分点,则以 = ,= 为基底时,用 ,表示
B
F
E ·
D ·
A C
4、若= -+3 , = 4 +2 , = - 3 +12, 写出用+ 的形式表示
【课堂小结】
(编者:杨学军)
2.3.2向量的坐标表示(1)
【学习目标】
能正确的用坐标来表示向量;
能区分向量的坐标与点的坐标的不同;
掌握平面向量的直角坐标运算;
提高分析问题的能力。
【预习指导】
1、一般地,对于向量 ,当它的起点移至_______时,其终点的坐标称为向量 的(直角)坐标,记作________________________。
2、有向线段AB的端点坐标为,则向量 的坐标为__________________________________________________。
3、若= ,
+=_________________________。
________________________。
【典型例题选讲】
例1:如图,已知O是坐标原点,点A在第一象限, ,求向量 的坐标。
例2:已知A(-1,3),B(1,-3),C (4 ,1) , D (3 ,4), 求向量 的坐标。
例3:平面上三点A(-2,1),B(-1,3),C(3,4),求D点坐标,使A,B,C,D这四个点构成平行四边形的四个顶点。
例4:已知P1( ),P2( ),P是直线P1P2上一点,且,求P的坐标。
【课堂练习】
1、与向量 平行的单位向量为__________________________________
2、若O(0,0),B(-1,3) 且 =3,则 坐标是:___________________
3、已知O是坐标原点,点A在第二象限, =2 , 求向量 的坐标。
4、已知边长为2的正三角形ABC,顶点A在坐标原点,AB边在 x轴上,点C在第一象限,D为AC的中点,分别求 的坐标。
【课堂小结】
(编者:杨学军)
2.3.2 向量的坐标表示(2)
【学习目标】
进一步掌握向量的坐标表示;
理解向量平行坐标表示的推导过程;
提高运用向量的坐标表示解决问题的能力。
【预习指导】
向量平行的线性表示是_____________________________
2、向量平行的坐标表示是:设 , ,如果∥ ,那么_________________,反之也成立。
3、已知A ,B ,C ,O四点满足条件: ,当 ,则能得到
________________________________________
【典型例题选讲】
例1:已知( , , ,并且 ,求证:∥。
例2:已知,当实数为何值时,向量与平行?并确定此时它们是同向还是反向。
例3:已知点O , A , B , C , 的坐标分别为(0,0),(3,4),(-1,2),(1,1),是否存在常数,成立?解释你所得结论的几何意义。
【课堂练习】
已知且∥,求实数的值。
已知,平行四边形ABCD的三个顶点的坐标分别为A (2, 1), B (-1,3) , C (3,4), 求第四个顶点的D坐标。
已知A (0, -2),B (2, 2),C (3, 4),求证:A,B,C三点共线。
已知向量,求与向量同方向的单位向量。
若两个向量方向相同,求。
【课堂小结】
(编者:杨学军)
2.4.1向量的数量积(1)
【学习目标】
理解平面向量数量积的概念及其几何意义
掌握数量积的运算法则
了解平面向量数量积与投影的关系
【预习指导】
1. 已知两个非零向量与,它们的夹角为,则把数量_________________叫做向量与的数量积(或内积)。
规定:零向量与任何一向量的数量积为_____________
2. 已知两个非零向量与,作,,则______________________叫做向量与的夹角。
当时,与___________,当时,与_________;当时,则称与__________。
3. 对于,其中_____________叫做在方向上的投影。
4. 平面向量数量积的性质
若与是非零向量,是与方向相同的单位向量,是与的夹角,则:
①;
②;
③;
④若与同向,则;若与反向,则;
或
⑤设是与的夹角,则。
5. 数量积的运算律
①交换律:________________________________
②数乘结合律:_________________________
③分配律:_____________________________
注:①、要区分两向量数量积的运算性质与数乘向量,实数与实数之积之间的差异。
②、数量积得运算只适合交换律,加乘分配律及数乘结合律,但不适合乘法结合律。即 不一定等于 ,也不适合消去律 。
【典型例题选讲】
例1: 已知向量 与向量 的夹角为 , = 2 , = 3 ,分别在下列条件下求:(1) = 135 ; (2) ∥ ; (3)
例2:已知 = 4 , = 8 ,且与的夹角为120 。
计算:(1) ;
(2) 。
例3:已知 = 4 , = 6 ,与的夹角为60 ,
求:(1)、 (2)、 (3)、
例4:已知向量 , =1 ,对任意t R ,恒有 ,则( )
A、 B、 (
C、 ( D、(
【课堂练习】
已知 = 10 , = 12 ,且 ,则与的夹角为__________
已知 、 、 是三个非零向量,试判断下列结论是否正确:
(1)、若,则 ∥ ( )
(2)、若,则 ( )
(3)、若,则 ( )
3、已知,则__________
4、四边形ABCD满足A = D ,则四边形ABCD是( )
A、平行四边形 B、矩形
C、菱形 D、正方形
5、正 边长为a ,则__________
【课堂小结】
(编者:杨学军)
2.4.1向量的数量积(2)
【学习目标】
能够理解和熟练运用模长公式,两点距离公式及夹角公式;
理解并掌握两个向量垂直的条件。
【预习指导】
1、若 则______________________________
2、向量的模长公式:
设则= cos = __________
两点间距离公式
设A( B 则__________
向量的夹角公式:
设= ( , , 与的夹角为 ,则有__________
两个向量垂直:
设= ( ,,
____________________
注意:对零向量只定义了平行,而不定义垂直。
【典例选讲】
例1:已知 = (2 , , ,求 。
例2:在中,设 且为直角三角形,求的值 。
例3:设向量,其中= (1,0),=(0,1)
(1)、试计算及的值。
(2)、求向量与的夹角大小。
【课堂练习】
1、已知 ,求:
2、已知向量,若与垂直,则实数=__________
3、已知若与平行,则__________
4、已知A、B、C是平面上的三个点,其坐标分别为 .那么=__________ , __________ , 的形状为__________
5、已知 ,且 与的夹角为钝角,求实数的取值范围。
【课堂小结】
(编者:杨学军)
2.1 向量的概念及表示
【学习目标】
1.了解向量的实际背景,理解平面向量的概念和向量的几何表示;掌握向量的模、零向量、单位向量、平行向量、相等向量、共线向量的概念;并会区分平行向量、相等向量和共线向量;
2.通过对向量的学习,使学生初步认识现实生活中的向量和数量的本质区别;
3.通过学生对向量与数量的识别能力的训练,培养学生认识客观事物的数学本质的能力。
【学习重难点】
重点:平行向量的概念和向量的几何表示;
难点:区分平行向量、相等向量和共线向量;
【自主学习】
1.向量的定义:__________________________________________________________;
2.向量的表示:
(1)图形表示:
(2)字母表示:
3.向量的相关概念:
(1)向量的长度(向量的模):_______________________记作:______________
(2)零向量:___________________,记作:_____________________
(3)单位向量:________________________________
(4)平行向量:________________________________
(5)共线向量:________________________________
(6)相等向量与相反向量:_________________________
思考:
(1)平面直角坐标系中,起点是原点的单位向量,它们的终点的轨迹是什么图形?____
(2)平行向量与共线向量的关系:____________________________________________
(3)向量“共线”与几何中“共线”有何区别:__________________________________
【典型例题】
例1.判断下例说法是否正确,若不正确请改正:
(1)零向量是唯一没有方向的向量;
(2)平面内的向量单位只有一个;
(3)方向相反的向量是共线向量,共线向量不一定是相反向量;
(4)向量和是共线向量,,则和是方向相同的向量;
(5)相等向量一定是共线向量;
例2.已知是正六边形的中心,在图中标出的向量中:
(1)试找出与共线的向量;
(2)确定与相等的向量;
(3)与相等吗?
例3.如图所示的为的方格纸(每个小方格都是边长为1的正方形),试问:起点和终点都在小方格的顶点处且与向量相等的向量共有几个?与向量平行且模为的向量共有几个?与向量的方向相同且模为的向量共有多少个?
【课堂练习】
1.判断下列说法是否正确,若不正确请改正:
(1)向量和是共线向量,则四点必在一直线上;
(2)单位向量都相等;
(3)任意一向量与它的相反向量都不想等;
(4)四边形是平行四边形当且仅当;
(5)共线向量,若起点不同,则终点一定不同;
2.平面直角坐标系中,已知,则点构成的图形是__________
3.四边形中,,则四边形的形状是_________
4.设,则与方向相同的单位向量是______________
5.若分别是四边形的边的中点。
求证:
6.已知飞机从甲地北偏东的方向飞行到达乙地,再从乙地按南偏东的方向飞行到达丙地,再从丙地按西南方向飞行到达丁地,问:丁地在甲地的什么方向?丁地距甲地多远?
【课堂小结】
(编者:尹欣)
2.2.1 向量的加法
【学习目标】
1.掌握向量加法的定义;
2.会用向量加法的三角法则和向量的平行四边形法则作两个向量的和向量;
3.掌握向量加法的交换律和结合律,并会用它们进行向量计算
【学习重难点】
重点:向量加法的三角法则、平行四边形则和加法运算律;
难点:向量加法的三角法则、平行四边形则和加法运算律;
【自主学习】
1.向量的和、向量的加法:
已知向量和,______________________________________________________
则向量叫做与的和,记作:____________________________________
_________________________________叫做向量的加法
注意:两个向量的和向量还是一个向量;
2.向量加法的几何作法:
(1)三角形法则的步骤:
①
②
③
就是所做的
(2)平行四边形法则的步骤:
①
②
③
就是所做的
注意:向量加法的平行四边形法则,只适用于对两个不共线的向量相加,而向量加法的三角形法则对于任何两个向量都适用。
3.向量加法的运算律:
(1)向量加法的交换律:
_________________________________________
(2)向量加法的结合律:
_________________________________________
思考:如果平面内有个向量依次首尾相接组成一条封闭折线,那么这条向量的和是什么?________________
【例题讲解】
例1.如图,已知为正六边形的中心,作出下列向量:
(1) (2) (3)
例2.化简下列各式
(1) (2)
(3) (4)
例3.在长江南岸某处,江水以的速度向东流,渡船的速度为,渡船要垂直地渡过长江,其航向应如何确定?
【课堂练习】
1.已知,求作:
(1)
(2)
2.已知是平行四边形的交点,下列结论正确的有_________
(1) (2)
(3) (4)
3.设点是内一点,若,则点为的______心;
4.对于任意的,不等式成立吗?请说明理由。
【课堂小结】
(编者:尹欣)
2.2.2 向量的减法
【学习目标】
1.理解向量减法的概念;
2.会做两个向量的差;
3.会进行向量加、减得混合运算
4.培养学生的辩证思维能力和认识问题的能力
【学习重难点】
重点:三角形法则
难点:三角形法则,向量加、减混合运算
【自主学习】
1.向量的减法:
①与的差:若__________________,则向量叫做与的差,记为__________
②向量与的减法:求两个向量差的运算叫做向量的减法;
注意:向量的减法是向量加法的逆运算。
2.向量的减法的作图方法:
作法:①_______________________________
②________________________________
③________________________________
则
3.减去一个向量等于加上这个向量的相反向量
4.关于向量减法需要注意一下几点:
①在用三角形法则做向量减法时,只要记住连接两向量的终点,箭头指向被减向量即可.
②以向量为邻边作平行四边形,则两条对角线的向量为,这一结论在以后应用还是非常广泛,应加强理解;
③对于任意一点,,简记“终减起”,在解题中经常用到,必须记住.
【例题讲解】
例1.已知向量,求作向量:;
思考:如果,怎么做出?
例2.已知是平行四边形的对角线的交点,若试证明:
本题还可以考虑如下方法:
1.(1)
(2)
2.任意一个非零向量都可以表示为两个不共线的向量和。
例3.化简下列各式
(1)
(2)
(3)
【课堂练习】
1.在中,,,下列等式成立的有_____________
(1)
(2)
(3)
(4)
2.已知四边形的对角线与相交与点,且,
求证:四边形是平行四边形。
3.如图,是一个梯形,,分别是的中点,已知试用表示和
【课堂小结】
(编者:尹欣)
2.2.3 向量的数乘(1)
【学习目标】
1.掌握向量数乘的定义,会确定向量数乘后的方向和模;
2.掌握向量数乘的运算律,并会用它进行计算;
3.通过本课的学习,渗透类比思想和化归思想
【学习重难点】
重点:向量的数乘及运算律;
难点:向量的数乘及运算律;
【自主学习】
1.向量的数乘的定义:
一般地,实数与向量的积是一个向量,记作:_______;它的长度和方向规定如下:
(1)
(2)当时,_______________________;
当时,_______________________;
当时,_______________________;
______________________________叫做向量的数乘
2.向量的线性运算定义:
___________________________________________统称为向量的线性运算;
3.向量的数乘的作图:
已知作
当时,把按原来的方向变为原来的倍;
当时,把按原来的相反方向变为原来的倍;
4.向量的数乘满足的运算律:
设为任意实数,为任意向量,则
(1)结合律
______________________________________
(2)分配律
_______________________________________
注意:(1)向量本身具有“形”和“数”的双重特点,而在实数与向量的积得运算过程中,既要考虑模的大小,又要考虑方向,因此它是数形结合的具体应用,这一点提示我们研究向量不能脱离它的几何意义;
(2)向量的数乘及运算性质可类比整式的乘法来理解和记忆。
【典型例题】
例1.已知向量,求作:
(1)向量
(2)
例2.计算
(1)
(2)
(3)
注意:(1)向量的数乘与实数的数乘的区别:相同点:这两种运算都满足结合律和分配律。不同点:实数的数乘的结果(积)是一个实数,而向量的数乘的结果是一个向量。
(2)向量的线性运算的结果是一个向量,运算法则与多项式运算类似。
例3.已知是不共线的向量,,试用表示
例4.已知:中,为的中点,为的中点,相交于点,求证:
(1)
(2)
(3)
【课堂练习】
1.计算:
(1)
(2)
2.已知向量且求
3.在平行四边形中,为的中点,用来表示
4.如图,在中,为边的中线,为的重心,求向量
【课堂小结】
(编者:尹欣)
2.2.3 向量的数乘(2)
【学习目标】
1.理解并掌握向量的共线定理;
2.能运用向量共线定理证明简单的几何问题;
3.培养学生的逻辑思维能力
【学习重难点】
重点:向量的共线定理;
难点:向量的共线定理;
【自主学习】
1.向量的线性表示:
若果,则称向量可以用非零向量线性表示;
2.向量共线定理:
思考:向量共线定理中有这个限制条件,若无此条件,会有什么结果?
【典型例题】
例1.如图,分别是的边的中点,
(1)将用线性表示;
(2)求证:与共线;
例2.设是两个不共线的向量,已知,若三点共线,求的值。
变式:设是两个不共线的向量,已知
,求证:三点共线。
例3.如图,中,为直线上一点,
求证:
思考:
(1)当时,你能得到什么结论?
(2)上面所证的结论:表明:起点为,终点为直线上一点的向量可以用表示,那么两个不共线的向量可以表示平面上任意一个向量吗?
例4.已知向量其中不共线,向量,是否存在实数,使得与共线
例5.平面直角坐标系中,已知若点满足其中三点共线,求的值;
【课堂练习】
1.已知向量求证:为共线向量;
2.设是两个不共线的向量,若是共线向量,求的值。
3.求证:起点相同的三个非零向量的终点在同一直线上。
【课堂小结】
(编者:尹欣)
2.3.1 平面向量基本原理
【学习目标】
了解平面向量的基本定理及其意义;
掌握三点(或三点以上)的共线的证明方法:
提高学生分析问题、解决问题的能力。
【预习指导】
1、平面向量的基本定理
如果,是同一平面内两个不共线的向量,那么对于这一平面内的任一向量,有且只有一对实数,使=+
2.、基底:
平面向量的基本定理中的不共线的向量, ,称为这一平面内所有向量的一组基底。
思考:
向量作为基底必须具备什么条件?
一个平面的基底唯一吗?
答:(1)______________________________________________________
(2)______________________________________________________
3、向量的分解、向量的正交分解:
一个平面向量用一组基底 , 表示成=+的形式,我们称它为向量的分解,当, 互相垂直时,就称为向量的正交分解。
点共线的证明方法:___________________________________________
【典例选讲】
例1:如图:平行四边形ABCD的对角线AC和BD交于一点M , = , =试用 ,,表示 , , 和 。
D C
M
A B
例2: 设 , 是平面的一组基底,如果 =3 —2 , =4 + ,=8 —9,求证:A、B、D三点共线。
例3: 如图,在平行四边形ABCD中,点 M在 AB的延长线上,且 BM=AB,点N 在 BC上,且BN=BC ,用向量法证明: M、N、D 三点共线。
D C
N
A B M
【课堂练习】
1、若,是平面内所有向量的一组基底,则下面的四组向量中不能作为一组基底的( )
A、 —2 和+2
B 、与3
C、2+3和 - 4—6
D、+与
2、若,是平面内所有向量的一组基底,那么下列结论成立的是( )
A、若实数,使+=0,则==0
B、空间任意向量都可以表示为=+,,R
C、+,,R不一定表示平面内一个向量
D、对于这一平面内的任一向量 ,使=+的实数对,有无数对
3、三角形ABC中,若 D,E,F 依次是 四等分点,则以 = ,= 为基底时,用 ,表示
B
F
E ·
D ·
A C
4、若= -+3 , = 4 +2 , = - 3 +12, 写出用+ 的形式表示
【课堂小结】
(编者:杨学军)
2.3.2向量的坐标表示(1)
【学习目标】
能正确的用坐标来表示向量;
能区分向量的坐标与点的坐标的不同;
掌握平面向量的直角坐标运算;
提高分析问题的能力。
【预习指导】
1、一般地,对于向量 ,当它的起点移至_______时,其终点的坐标称为向量 的(直角)坐标,记作________________________。
2、有向线段AB的端点坐标为,则向量 的坐标为__________________________________________________。
3、若= ,
+=_________________________。
________________________。
【典型例题选讲】
例1:如图,已知O是坐标原点,点A在第一象限, ,求向量 的坐标。
例2:已知A(-1,3),B(1,-3),C (4 ,1) , D (3 ,4), 求向量 的坐标。
例3:平面上三点A(-2,1),B(-1,3),C(3,4),求D点坐标,使A,B,C,D这四个点构成平行四边形的四个顶点。
例4:已知P1( ),P2( ),P是直线P1P2上一点,且,求P的坐标。
【课堂练习】
1、与向量 平行的单位向量为__________________________________
2、若O(0,0),B(-1,3) 且 =3,则 坐标是:___________________
3、已知O是坐标原点,点A在第二象限, =2 , 求向量 的坐标。
4、已知边长为2的正三角形ABC,顶点A在坐标原点,AB边在 x轴上,点C在第一象限,D为AC的中点,分别求 的坐标。
【课堂小结】
(编者:杨学军)
2.3.2 向量的坐标表示(2)
【学习目标】
进一步掌握向量的坐标表示;
理解向量平行坐标表示的推导过程;
提高运用向量的坐标表示解决问题的能力。
【预习指导】
向量平行的线性表示是_____________________________
2、向量平行的坐标表示是:设 , ,如果∥ ,那么_________________,反之也成立。
3、已知A ,B ,C ,O四点满足条件: ,当 ,则能得到
________________________________________
【典型例题选讲】
例1:已知( , , ,并且 ,求证:∥。
例2:已知,当实数为何值时,向量与平行?并确定此时它们是同向还是反向。
例3:已知点O , A , B , C , 的坐标分别为(0,0),(3,4),(-1,2),(1,1),是否存在常数,成立?解释你所得结论的几何意义。
【课堂练习】
已知且∥,求实数的值。
已知,平行四边形ABCD的三个顶点的坐标分别为A (2, 1), B (-1,3) , C (3,4), 求第四个顶点的D坐标。
已知A (0, -2),B (2, 2),C (3, 4),求证:A,B,C三点共线。
已知向量,求与向量同方向的单位向量。
若两个向量方向相同,求。
【课堂小结】
(编者:杨学军)
2.4.1向量的数量积(1)
【学习目标】
理解平面向量数量积的概念及其几何意义
掌握数量积的运算法则
了解平面向量数量积与投影的关系
【预习指导】
1. 已知两个非零向量与,它们的夹角为,则把数量_________________叫做向量与的数量积(或内积)。
规定:零向量与任何一向量的数量积为_____________
2. 已知两个非零向量与,作,,则______________________叫做向量与的夹角。
当时,与___________,当时,与_________;当时,则称与__________。
3. 对于,其中_____________叫做在方向上的投影。
4. 平面向量数量积的性质
若与是非零向量,是与方向相同的单位向量,是与的夹角,则:
①;
②;
③;
④若与同向,则;若与反向,则;
或
⑤设是与的夹角,则。
5. 数量积的运算律
①交换律:________________________________
②数乘结合律:_________________________
③分配律:_____________________________
注:①、要区分两向量数量积的运算性质与数乘向量,实数与实数之积之间的差异。
②、数量积得运算只适合交换律,加乘分配律及数乘结合律,但不适合乘法结合律。即 不一定等于 ,也不适合消去律 。
【典型例题选讲】
例1: 已知向量 与向量 的夹角为 , = 2 , = 3 ,分别在下列条件下求:(1) = 135 ; (2) ∥ ; (3)
例2:已知 = 4 , = 8 ,且与的夹角为120 。
计算:(1) ;
(2) 。
例3:已知 = 4 , = 6 ,与的夹角为60 ,
求:(1)、 (2)、 (3)、
例4:已知向量 , =1 ,对任意t R ,恒有 ,则( )
A、 B、 (
C、 ( D、(
【课堂练习】
已知 = 10 , = 12 ,且 ,则与的夹角为__________
已知 、 、 是三个非零向量,试判断下列结论是否正确:
(1)、若,则 ∥ ( )
(2)、若,则 ( )
(3)、若,则 ( )
3、已知,则__________
4、四边形ABCD满足A = D ,则四边形ABCD是( )
A、平行四边形 B、矩形
C、菱形 D、正方形
5、正 边长为a ,则__________
【课堂小结】
(编者:杨学军)
2.4.1向量的数量积(2)
【学习目标】
能够理解和熟练运用模长公式,两点距离公式及夹角公式;
理解并掌握两个向量垂直的条件。
【预习指导】
1、若 则______________________________
2、向量的模长公式:
设则= cos = __________
两点间距离公式
设A( B 则__________
向量的夹角公式:
设= ( , , 与的夹角为 ,则有__________
两个向量垂直:
设= ( ,,
____________________
注意:对零向量只定义了平行,而不定义垂直。
【典例选讲】
例1:已知 = (2 , , ,求 。
例2:在中,设 且为直角三角形,求的值 。
例3:设向量,其中= (1,0),=(0,1)
(1)、试计算及的值。
(2)、求向量与的夹角大小。
【课堂练习】
1、已知 ,求:
2、已知向量,若与垂直,则实数=__________
3、已知若与平行,则__________
4、已知A、B、C是平面上的三个点,其坐标分别为 .那么=__________ , __________ , 的形状为__________
5、已知 ,且 与的夹角为钝角,求实数的取值范围。
【课堂小结】
(编者:杨学军)
