2022-2023学年上海市高二(上)期中数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年上海市高二(上)期中数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 00:00:00 | ||
图片预览




文档简介
2022-2023学年上海市高二(上)期中数学试卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共4小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
设,为空间两条不同的直线,,为空间两个不同的平面,给出下列命题:
若,,则;
若,,则;
若,且,,则;
若,且,则.
其中所有正确命题的序号是( )
A. B. C. D.
若一个水平放置的图形的斜二测直观图是一个底角为且腰和上底均为的等腰梯形,则原平面图形的面积是( )
A. B. C. D.
如图,上海海关大楼的钟楼可以看作一个正四棱柱,且钟楼的四个侧面均有时钟悬挂,在点到点时针与分针的转动中包括点,但不包括点,相邻两面时钟的时针两两相互垂直的情况的次数为( )
A. B. C. D.
年,东印度今孟加拉国学者森德拉姆发现了“正方形筛子”如图所示,根据规律,则“正方形筛子”中位于第行的第个数是( )
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共12小题,共36.0分)
若一个球的体积为,则该球的表面积为______.
正方体中,异面直线与所成的角的大小为______.
向量与夹角的大小为______.
正四棱锥底面边长为,侧棱长为,则其体积为______ .
在等差数列中,其前项和为,已知公差,,则______.
记数列的前项和为,若,为正整数,则数列的通项公式为______.
若表示等式为正偶数,则表示的等式为______.
一个圆锥的侧面展开图是圆心角为,半径为的扇形,则圆锥母线与底面所成角为______结果用反三角函数值表示
在长方体中,若长方体的体对角线与过点的相邻三个面所成的角分别为,,,则______.
已知,,,分别是空间四边形各边,,,的中点,若,,则______.
如图所示,在中,,,在三角形内挖去半圆圆心在边上,半圆与,相切于点,,与交于点,则图中阴影部分绕直线旋转一周所得旋转体的体积为______.
如图,在棱长为的正方体中,为底面内包括边界的动点,满足与直线所成角的大小为,则线段扫过的面积为______.
三、解答题(本大题共4小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
本小题分
如图,已知正方体的棱长为,点是棱的中点.
求异面直线与所成角的大小;
求直线与平面所成的角的大小.结果用反三角函数值表示
本小题分
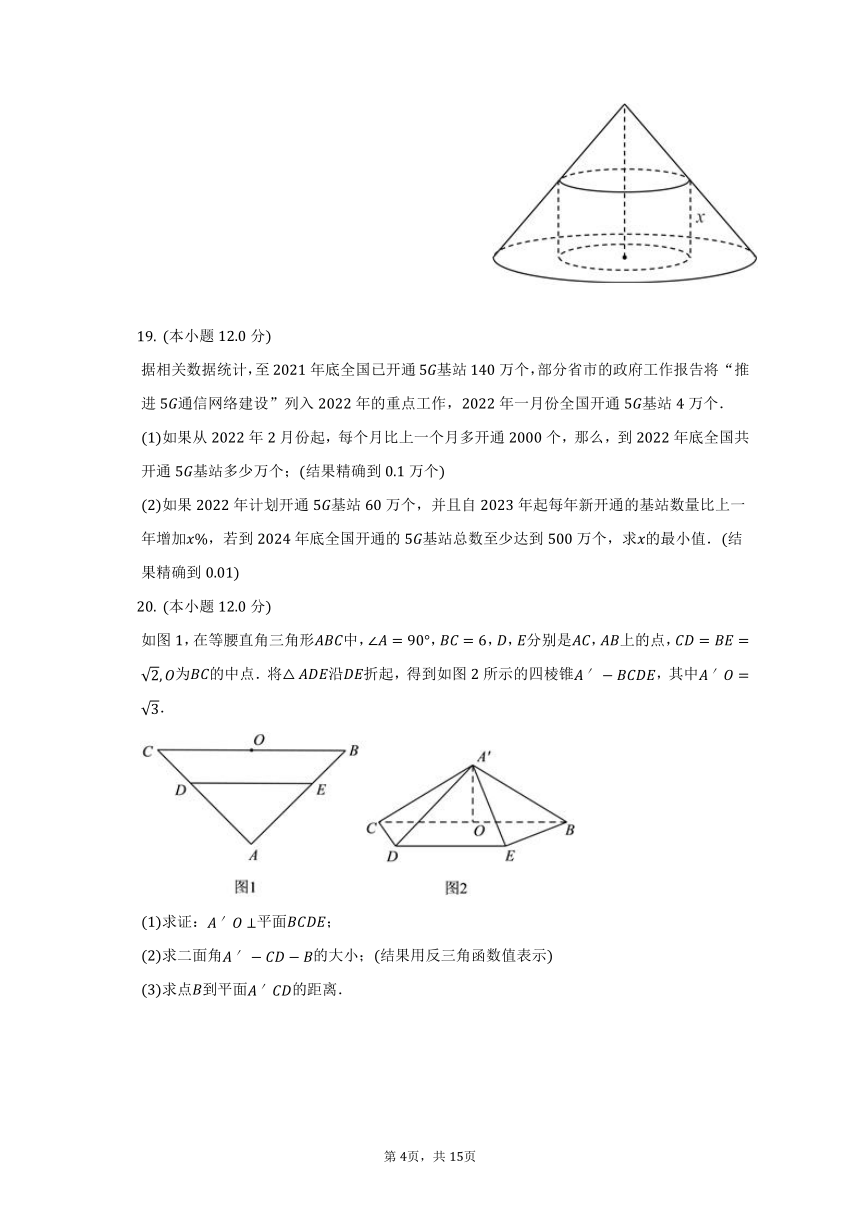
如图,已知一个圆锥的底面半径为,高为,且在这个圆锥中有一个高为的圆柱.
当时,求圆柱的体积;
当为何值时,此圆柱的侧面积最大,并求出此最大值.
本小题分
据相关数据统计,至年底全国已开通基站万个,部分省市的政府工作报告将“推进通信网络建设”列入年的重点工作,年一月份全国开通基站万个.
如果从年月份起,每个月比上一个月多开通个,那么,到年底全国共开通基站多少万个;结果精确到万个
如果年计划开通基站万个,并且自年起每年新开通的基站数量比上一年增加,若到年底全国开通的基站总数至少达到万个,求的最小值.结果精确到
本小题分
如图,在等腰直角三角形中,,,,分别是,上的点,为的中点.将沿折起,得到如图所示的四棱锥,其中.
求证:平面;
求二面角的大小;结果用反三角函数值表示
求点到平面的距离.
答案和解析
1.【答案】
【解析】
【分析】
本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
在中,由面面垂直的判定定理得;在中,与相交、平行或异面;在中,与相交或平行;在中,由线面垂直的性质定理得.
【解答】
解:由,为空间两条不同的直线,,为空间两个不同的平面,知:
在中,若,,则由面面垂直的判定定理得,故正确;
在中,若,,则与相交、平行或异面,故错误;
在中,若,且,,则与相交或平行,故错误;
在中,若,且,则由线面垂直的性质定理得,故正确.
其中所有正确命题的序号是.
故选:.
2.【答案】
【解析】解:水平放置的图形为一直角梯形,由题意可知上底为,高为,下底为,
.
故选:.
水平放置的图形为直角梯形,求出上底,高,下底,利用梯形面积公式求解即可.
本题考查水平放置的平面图形的直观图斜二测画法,也可利用原图和直观图的面积关系求解.属基础知识的考查.
3.【答案】
【解析】解:当时针在时或时相互垂直,时或时时针平行,其它时间时针所在直线异面但不垂直,所以能够垂直次.
故选:.
根据正四棱柱相邻侧面的线线关系即可判断出结论.
本题考查了正四棱柱相邻侧面的线线关系,考查了推理能力与计算能力,属于基础题.
4.【答案】
【解析】解:第一列的数字为,,,,,,成等差数列,公差,
其通项公式,故第行的第一个数为,
再看行,第一行的数是公差为的等差数列,第二行的数是公差为的等差数列,第三行的数是公差为的等差数列,,第行的数是公差为的等差数列,
则第行的数是公差为的等差数列,
所以第行的第个数是.
故选:.
先求出第行的第一个数,再根据第行的数是公差为的等差数列,从而得到第行的第个数是.
本题考查归纳推理,等差数列的概念与通项公式的应用,属中档题.
5.【答案】
【解析】
【试题解析】
【分析】
本题考查球的体积和表面积的应用,解题时要认真审题,仔细解答.
由球的体积,由球的体积公式能求出这个球的半径,再由球的表面积的计算公式能求出结果.
【解答】
解:一个球的体积,
设这个球的半径,则,
故答案为:.
6.【答案】
【解析】解:如图所示,直线,所以直线与所成的角即为异面直线与所成角.为正三角形,.
故答案为:.
如图所示,连接,,则即为异面直线与所成角.利用为正三角形,即可得出.
本题考查正方体的性质、等边三角形的性质、异面直线所成的角,考查推理能力与计算能力,属于中档题.
7.【答案】
【解析】解:向量,,
设与的夹角为,则,
,.
故答案为:.
利用向量夹角公式求解即可.
本题主要考查空间向量夹角的求法,考查运算求解能力,属于基础题.
8.【答案】
【解析】解:如图,正四棱锥中,,,
设正四棱锥的高为,连结,
则.
在直角三角形中,.
所以.
故答案为.
由正四棱锥的底面边长求出底面中心到一个顶点的距离,结合侧棱长求出正四棱锥的高,然后直接利用体积公式求体积.
本题考查了棱锥的体积,解答的关键是熟悉正四棱锥中几个直角三角形,考查了棱锥体积公式的记忆,是基础题.
9.【答案】
【解析】解:由题意得,
解得,
,
.
故答案为:.
由已知条件可求得,得出,进而由得出答案.
本题主要考查了等差数列的通项公式及求和公式,属于基础题.
10.【答案】
【解析】解:,,;
,;
可得:,;
当时,,即时不满足;
数列从第二项开始起以为首项,为公比的等比数列;
.
故答案为:.
利用通项和前项和之间的关系求解即可.
本题考查了数列的递推公式,考查学生对知识的运用能力,属于中档题.
11.【答案】
【解析】解:将代入等式,得到.
故答案为:.
代入,得到.
本题考查归纳推理,属基础题.
12.【答案】
【解析】解:设母线长为,底面圆的半径为,
因为圆锥的侧面展开图是圆心角为,半径为的扇形,
所以,且,解得,
设圆锥的母线与底面所成角为,则,
所以圆锥的母线与底面所成角为.
故答案为:.
设母线长为,底面圆的半径为,圆锥侧面展开图的弧长等于底面周长,半径等于圆锥的母线长,分别求出,,由线面角的定义求解即可.
本题主要考查圆锥的侧面积,圆锥的结构特征,考查运算求解能力,属于中档题.
13.【答案】
【解析】解:连接,,,在长方体中,面,
与面所成的角为,
,
同理与面所成的角为,
,与面所成的角为,,
.
故答案为:.
由已知得,由此即可求出答案.
本题考查线面角的定义及其求解,考查运算求解能力,属于中档题.
14.【答案】
【解析】解:如图所示,
由三角形中位线的性质可得,,
则,,所以四边形是平行四边形,
则,
又,,
所以 ,即.
故答案为:.
根据中位线定理判断四边形是平行四边形,再由计算可得解.
本题考查空间向量在立体几何中的运用,考查转化思想以及运算求解能力,属于中档题.
15.【答案】
【解析】解:几何体是图中阴影部分绕直线旋转一周所得旋转体,
是一个圆锥内挖去一个球后剩余部分,
且球是圆锥的内切球,
所以圆锥的底面半径是,高为,球的半径为,
可以得到,
所以圆锥的体积为,
球的体积为,
所以阴影部分绕直线旋转一周所得旋转体的体积为,
故答案为:.
几何体是图中阴影部分绕直线旋转一周所得旋转体,是一个圆锥内挖去一个球后剩余部分,求出圆锥的体积减去球的体积,可得几何体的体积.
该题考查的是有关旋转体的体积的求解问题,在解题的过程中,注意分析几何体的特征,涉及到的知识点有锥体的体积公式和球的体积公式,属于简单题目.
16.【答案】
【解析】解:因为,
所以与直线所成角可转化为与直线所成角,即,
在中,,,
所以,
所以点在底面内的轨迹是以为半径的圆的四分之一,
所以线段扫过的面积为
故答案为:
由,知与直线所成角为与直线所成角,即,而点在底面内的轨迹是以为半径的圆的四分之一,再求得的长,即可得解.
本题考查异面直线所成角,动点的轨迹问题,考查空间立体感、逻辑推理能力和运算能力,属于基础题.
17.【答案】解:取的中点,连接,,如图,
则或其补角为异面直线与所成角,
因为正方体的棱长为,
所以,
由余弦定理得,
所以异面直线与所成角的大小为;
因为平面,
所以是直线与平面所成的角,
在中,,,,
所以直线与平面所成的角为.
【解析】取的中点,连接,,则或其补角为异面直线与所成角,利用余弦定理进行求解即可.
因为平面,所以是直线与平面所成的角,在中求解即可.
本题考查异面直线所成角的求解,线面角的求解,属中档题.
18.【答案】解:设圆柱的半径为,
由题意得,即,,
当时,则,
故圆柱的体积;
由得,,
则圆柱的侧面积,
当时,圆柱的侧面积取最大值.
【解析】设圆柱的底面半径为,利用可得与的关系,结合题意,即可得出答案;
由得,结合圆柱的侧面积公式,利用二次函数的性质,即可得出答案.
本题考查棱柱、棱锥的体积,考查转化思想、数形结合思想和函数思想,考查逻辑推理能力和运算能力,属于中档题.
19.【答案】解:年每月开通的基站数量构成一个等差数列,公差为万,首项为万,
则年开通的基站数为万个,
故到年底全国共开通基站万个;
由题意得,
即,解得,
,即,
所以的最小值为.
【解析】年每月开通基站的数量构成一个等差数列,公差为万,首项为万,求出年开通的基站数,加上得答案;
由题意得,求解即可.
本题考查根据实际问题选择函数模型,考查运算求解能力,属于基础题.
20.【答案】解:连接,,
在等腰直角中,,
在中,由余弦定理得,
在中,由余弦定理得,
,
,,
,
,,
又,平面,平面,
平面;
取中点,则,
建立以为坐标原点,以,,所在直线分别为,,轴的空间直角坐标系,如图所示:
则,
平面的一个法向量为,
设平面的法向量为,,
则,取,则,
平面的一个法向量,
设二面角的平面角为,且由图形得为锐角,
所以,
故二面角的大小为;
由得平面的一个法向量,
又,,则,
点到平面的距离为.
【解析】利用余弦定理求出,,利用勾股定理逆定理可得,根据线面垂直的判定定理,即可证明结论;
取中点,则以为坐标原点,,,分别为,,轴建立空间直角坐标系,利用向量法,即可得出答案;
由得平面的一个法向量,利用向量法,即可得出答案.
本题考查直线与平面垂直的判定定理、二面角、点到平面的距离及空间向量的应用,考查转化思想和数形结合思想,考查逻辑推理能力和运算能力,属于中档题.
第1页,共1页
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共4小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
设,为空间两条不同的直线,,为空间两个不同的平面,给出下列命题:
若,,则;
若,,则;
若,且,,则;
若,且,则.
其中所有正确命题的序号是( )
A. B. C. D.
若一个水平放置的图形的斜二测直观图是一个底角为且腰和上底均为的等腰梯形,则原平面图形的面积是( )
A. B. C. D.
如图,上海海关大楼的钟楼可以看作一个正四棱柱,且钟楼的四个侧面均有时钟悬挂,在点到点时针与分针的转动中包括点,但不包括点,相邻两面时钟的时针两两相互垂直的情况的次数为( )
A. B. C. D.
年,东印度今孟加拉国学者森德拉姆发现了“正方形筛子”如图所示,根据规律,则“正方形筛子”中位于第行的第个数是( )
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共12小题,共36.0分)
若一个球的体积为,则该球的表面积为______.
正方体中,异面直线与所成的角的大小为______.
向量与夹角的大小为______.
正四棱锥底面边长为,侧棱长为,则其体积为______ .
在等差数列中,其前项和为,已知公差,,则______.
记数列的前项和为,若,为正整数,则数列的通项公式为______.
若表示等式为正偶数,则表示的等式为______.
一个圆锥的侧面展开图是圆心角为,半径为的扇形,则圆锥母线与底面所成角为______结果用反三角函数值表示
在长方体中,若长方体的体对角线与过点的相邻三个面所成的角分别为,,,则______.
已知,,,分别是空间四边形各边,,,的中点,若,,则______.
如图所示,在中,,,在三角形内挖去半圆圆心在边上,半圆与,相切于点,,与交于点,则图中阴影部分绕直线旋转一周所得旋转体的体积为______.
如图,在棱长为的正方体中,为底面内包括边界的动点,满足与直线所成角的大小为,则线段扫过的面积为______.
三、解答题(本大题共4小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
本小题分
如图,已知正方体的棱长为,点是棱的中点.
求异面直线与所成角的大小;
求直线与平面所成的角的大小.结果用反三角函数值表示
本小题分
如图,已知一个圆锥的底面半径为,高为,且在这个圆锥中有一个高为的圆柱.
当时,求圆柱的体积;
当为何值时,此圆柱的侧面积最大,并求出此最大值.
本小题分
据相关数据统计,至年底全国已开通基站万个,部分省市的政府工作报告将“推进通信网络建设”列入年的重点工作,年一月份全国开通基站万个.
如果从年月份起,每个月比上一个月多开通个,那么,到年底全国共开通基站多少万个;结果精确到万个
如果年计划开通基站万个,并且自年起每年新开通的基站数量比上一年增加,若到年底全国开通的基站总数至少达到万个,求的最小值.结果精确到
本小题分
如图,在等腰直角三角形中,,,,分别是,上的点,为的中点.将沿折起,得到如图所示的四棱锥,其中.
求证:平面;
求二面角的大小;结果用反三角函数值表示
求点到平面的距离.
答案和解析
1.【答案】
【解析】
【分析】
本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
在中,由面面垂直的判定定理得;在中,与相交、平行或异面;在中,与相交或平行;在中,由线面垂直的性质定理得.
【解答】
解:由,为空间两条不同的直线,,为空间两个不同的平面,知:
在中,若,,则由面面垂直的判定定理得,故正确;
在中,若,,则与相交、平行或异面,故错误;
在中,若,且,,则与相交或平行,故错误;
在中,若,且,则由线面垂直的性质定理得,故正确.
其中所有正确命题的序号是.
故选:.
2.【答案】
【解析】解:水平放置的图形为一直角梯形,由题意可知上底为,高为,下底为,
.
故选:.
水平放置的图形为直角梯形,求出上底,高,下底,利用梯形面积公式求解即可.
本题考查水平放置的平面图形的直观图斜二测画法,也可利用原图和直观图的面积关系求解.属基础知识的考查.
3.【答案】
【解析】解:当时针在时或时相互垂直,时或时时针平行,其它时间时针所在直线异面但不垂直,所以能够垂直次.
故选:.
根据正四棱柱相邻侧面的线线关系即可判断出结论.
本题考查了正四棱柱相邻侧面的线线关系,考查了推理能力与计算能力,属于基础题.
4.【答案】
【解析】解:第一列的数字为,,,,,,成等差数列,公差,
其通项公式,故第行的第一个数为,
再看行,第一行的数是公差为的等差数列,第二行的数是公差为的等差数列,第三行的数是公差为的等差数列,,第行的数是公差为的等差数列,
则第行的数是公差为的等差数列,
所以第行的第个数是.
故选:.
先求出第行的第一个数,再根据第行的数是公差为的等差数列,从而得到第行的第个数是.
本题考查归纳推理,等差数列的概念与通项公式的应用,属中档题.
5.【答案】
【解析】
【试题解析】
【分析】
本题考查球的体积和表面积的应用,解题时要认真审题,仔细解答.
由球的体积,由球的体积公式能求出这个球的半径,再由球的表面积的计算公式能求出结果.
【解答】
解:一个球的体积,
设这个球的半径,则,
故答案为:.
6.【答案】
【解析】解:如图所示,直线,所以直线与所成的角即为异面直线与所成角.为正三角形,.
故答案为:.
如图所示,连接,,则即为异面直线与所成角.利用为正三角形,即可得出.
本题考查正方体的性质、等边三角形的性质、异面直线所成的角,考查推理能力与计算能力,属于中档题.
7.【答案】
【解析】解:向量,,
设与的夹角为,则,
,.
故答案为:.
利用向量夹角公式求解即可.
本题主要考查空间向量夹角的求法,考查运算求解能力,属于基础题.
8.【答案】
【解析】解:如图,正四棱锥中,,,
设正四棱锥的高为,连结,
则.
在直角三角形中,.
所以.
故答案为.
由正四棱锥的底面边长求出底面中心到一个顶点的距离,结合侧棱长求出正四棱锥的高,然后直接利用体积公式求体积.
本题考查了棱锥的体积,解答的关键是熟悉正四棱锥中几个直角三角形,考查了棱锥体积公式的记忆,是基础题.
9.【答案】
【解析】解:由题意得,
解得,
,
.
故答案为:.
由已知条件可求得,得出,进而由得出答案.
本题主要考查了等差数列的通项公式及求和公式,属于基础题.
10.【答案】
【解析】解:,,;
,;
可得:,;
当时,,即时不满足;
数列从第二项开始起以为首项,为公比的等比数列;
.
故答案为:.
利用通项和前项和之间的关系求解即可.
本题考查了数列的递推公式,考查学生对知识的运用能力,属于中档题.
11.【答案】
【解析】解:将代入等式,得到.
故答案为:.
代入,得到.
本题考查归纳推理,属基础题.
12.【答案】
【解析】解:设母线长为,底面圆的半径为,
因为圆锥的侧面展开图是圆心角为,半径为的扇形,
所以,且,解得,
设圆锥的母线与底面所成角为,则,
所以圆锥的母线与底面所成角为.
故答案为:.
设母线长为,底面圆的半径为,圆锥侧面展开图的弧长等于底面周长,半径等于圆锥的母线长,分别求出,,由线面角的定义求解即可.
本题主要考查圆锥的侧面积,圆锥的结构特征,考查运算求解能力,属于中档题.
13.【答案】
【解析】解:连接,,,在长方体中,面,
与面所成的角为,
,
同理与面所成的角为,
,与面所成的角为,,
.
故答案为:.
由已知得,由此即可求出答案.
本题考查线面角的定义及其求解,考查运算求解能力,属于中档题.
14.【答案】
【解析】解:如图所示,
由三角形中位线的性质可得,,
则,,所以四边形是平行四边形,
则,
又,,
所以 ,即.
故答案为:.
根据中位线定理判断四边形是平行四边形,再由计算可得解.
本题考查空间向量在立体几何中的运用,考查转化思想以及运算求解能力,属于中档题.
15.【答案】
【解析】解:几何体是图中阴影部分绕直线旋转一周所得旋转体,
是一个圆锥内挖去一个球后剩余部分,
且球是圆锥的内切球,
所以圆锥的底面半径是,高为,球的半径为,
可以得到,
所以圆锥的体积为,
球的体积为,
所以阴影部分绕直线旋转一周所得旋转体的体积为,
故答案为:.
几何体是图中阴影部分绕直线旋转一周所得旋转体,是一个圆锥内挖去一个球后剩余部分,求出圆锥的体积减去球的体积,可得几何体的体积.
该题考查的是有关旋转体的体积的求解问题,在解题的过程中,注意分析几何体的特征,涉及到的知识点有锥体的体积公式和球的体积公式,属于简单题目.
16.【答案】
【解析】解:因为,
所以与直线所成角可转化为与直线所成角,即,
在中,,,
所以,
所以点在底面内的轨迹是以为半径的圆的四分之一,
所以线段扫过的面积为
故答案为:
由,知与直线所成角为与直线所成角,即,而点在底面内的轨迹是以为半径的圆的四分之一,再求得的长,即可得解.
本题考查异面直线所成角,动点的轨迹问题,考查空间立体感、逻辑推理能力和运算能力,属于基础题.
17.【答案】解:取的中点,连接,,如图,
则或其补角为异面直线与所成角,
因为正方体的棱长为,
所以,
由余弦定理得,
所以异面直线与所成角的大小为;
因为平面,
所以是直线与平面所成的角,
在中,,,,
所以直线与平面所成的角为.
【解析】取的中点,连接,,则或其补角为异面直线与所成角,利用余弦定理进行求解即可.
因为平面,所以是直线与平面所成的角,在中求解即可.
本题考查异面直线所成角的求解,线面角的求解,属中档题.
18.【答案】解:设圆柱的半径为,
由题意得,即,,
当时,则,
故圆柱的体积;
由得,,
则圆柱的侧面积,
当时,圆柱的侧面积取最大值.
【解析】设圆柱的底面半径为,利用可得与的关系,结合题意,即可得出答案;
由得,结合圆柱的侧面积公式,利用二次函数的性质,即可得出答案.
本题考查棱柱、棱锥的体积,考查转化思想、数形结合思想和函数思想,考查逻辑推理能力和运算能力,属于中档题.
19.【答案】解:年每月开通的基站数量构成一个等差数列,公差为万,首项为万,
则年开通的基站数为万个,
故到年底全国共开通基站万个;
由题意得,
即,解得,
,即,
所以的最小值为.
【解析】年每月开通基站的数量构成一个等差数列,公差为万,首项为万,求出年开通的基站数,加上得答案;
由题意得,求解即可.
本题考查根据实际问题选择函数模型,考查运算求解能力,属于基础题.
20.【答案】解:连接,,
在等腰直角中,,
在中,由余弦定理得,
在中,由余弦定理得,
,
,,
,
,,
又,平面,平面,
平面;
取中点,则,
建立以为坐标原点,以,,所在直线分别为,,轴的空间直角坐标系,如图所示:
则,
平面的一个法向量为,
设平面的法向量为,,
则,取,则,
平面的一个法向量,
设二面角的平面角为,且由图形得为锐角,
所以,
故二面角的大小为;
由得平面的一个法向量,
又,,则,
点到平面的距离为.
【解析】利用余弦定理求出,,利用勾股定理逆定理可得,根据线面垂直的判定定理,即可证明结论;
取中点,则以为坐标原点,,,分别为,,轴建立空间直角坐标系,利用向量法,即可得出答案;
由得平面的一个法向量,利用向量法,即可得出答案.
本题考查直线与平面垂直的判定定理、二面角、点到平面的距离及空间向量的应用,考查转化思想和数形结合思想,考查逻辑推理能力和运算能力,属于中档题.
第1页,共1页
同课章节目录
