任意角的三角函数[上学期]

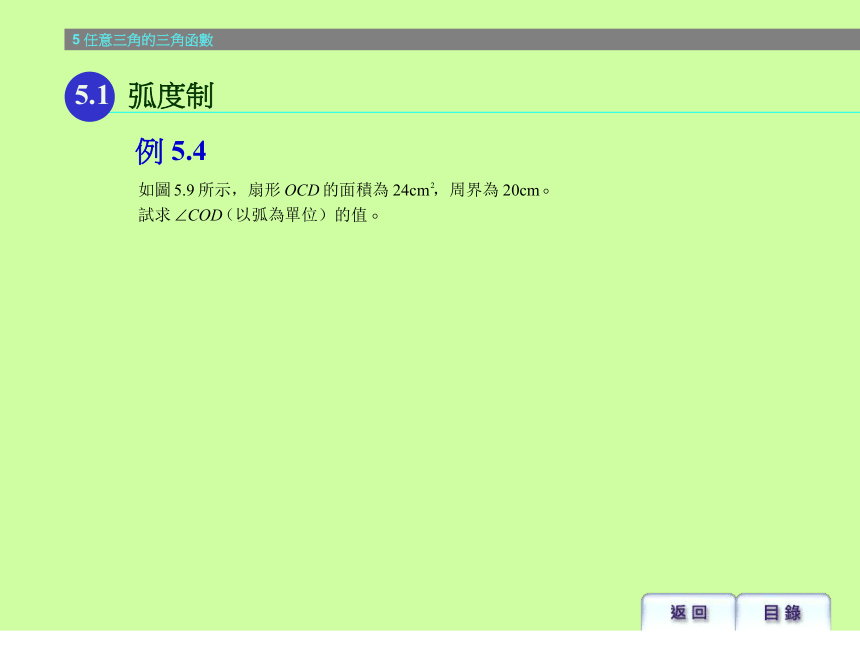
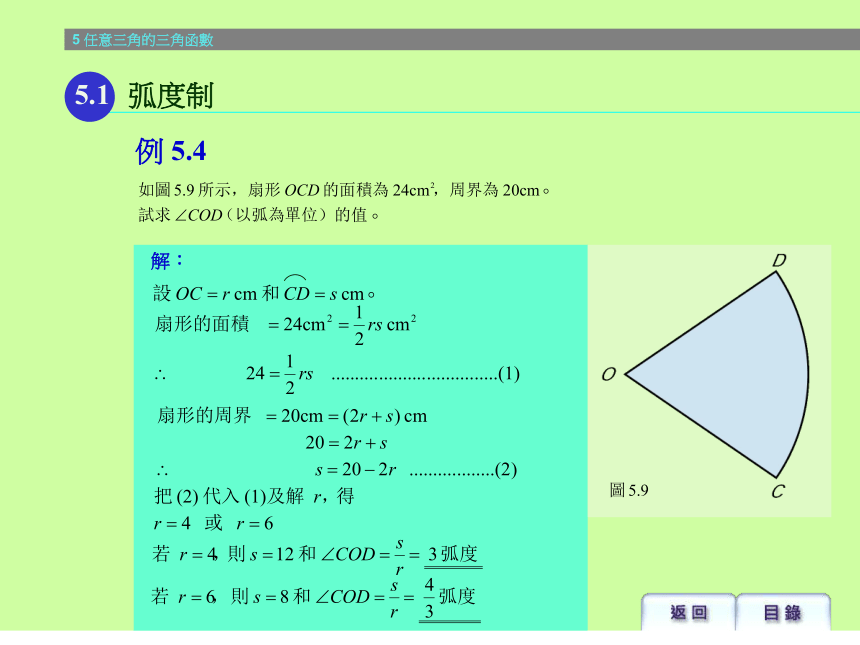
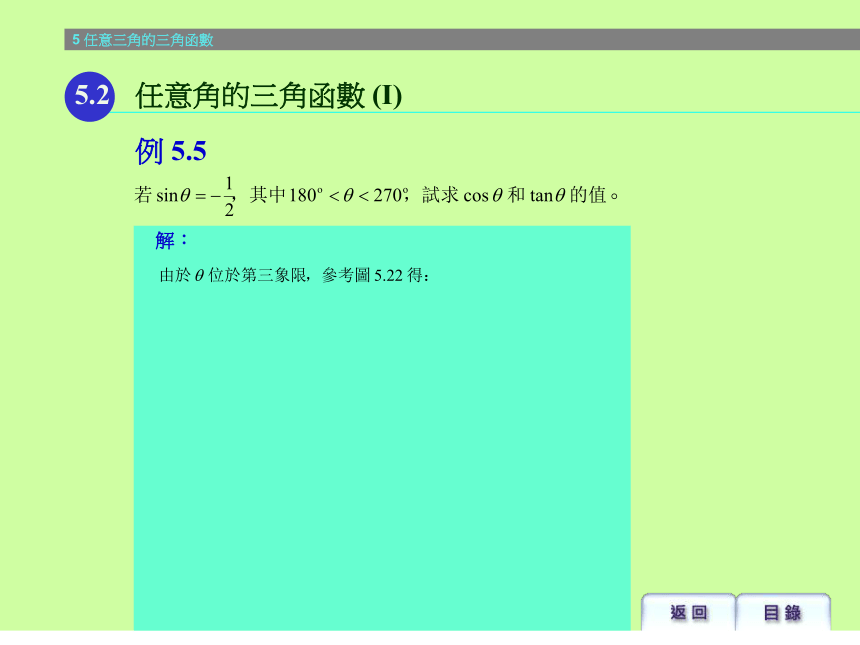
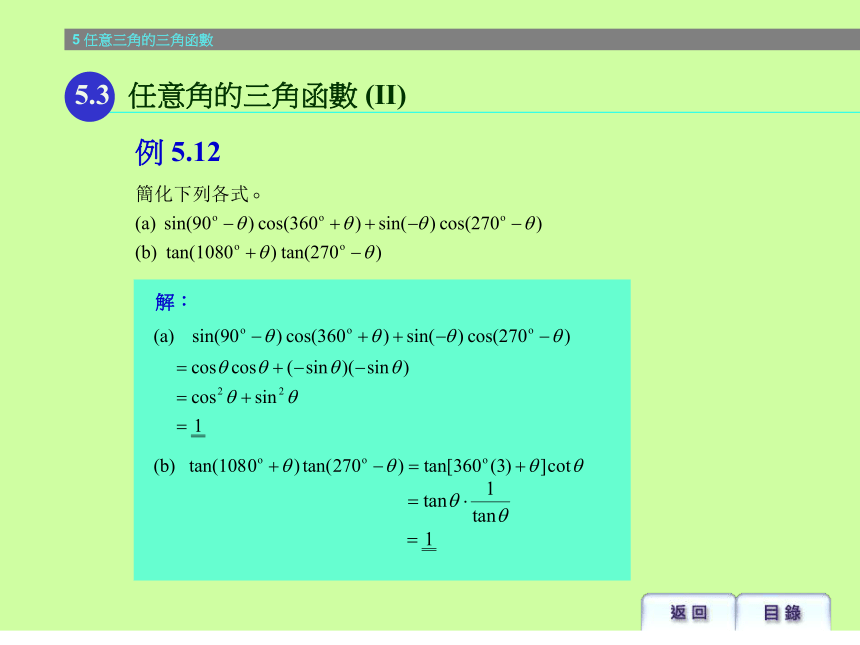
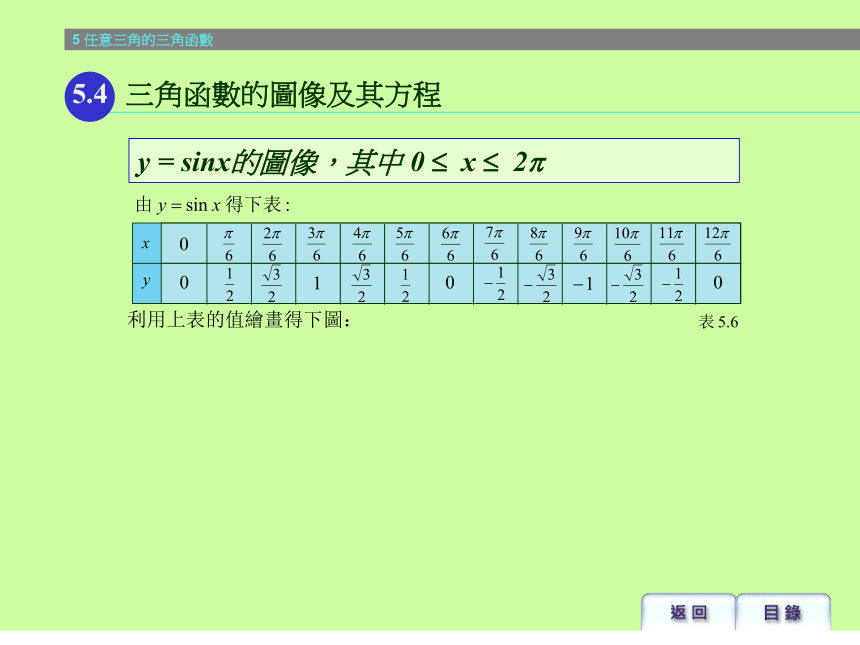
课件49张PPT。解：5.1 弧度制例 5.35解：5.1 弧度制例 5.3任意角的三角函數例 5.45.1 弧度制解：例 5.45.1 弧度制解：例 5.55.2 任意角的三角函數 (I)因為 P 點在第三象限，所以x<0。解：例 5.55.2 任意角的三角函數 (I)證明：例 5.7 根據商數關係 根據平方關係 根據倒數關係5.2 任意角的三角函數 (I)解：例 5.9 由於 tan? < 0，故捨去正號。5.2 任意角的三角函數 (I)解：例 5.105.2 任意角的三角函數 (I)解：例 5.115.3 任意角的三角函數 (II) sin (360o – ? )= – sin ? tan (360on + ? )= tan ?， 其中 n 是整數 sin (– ? )= – sin ? sin (180 o – ? )= sin ?解：例 5.125.3 任意角的三角函數 (II)5.4 三角函數的圖像及其方程y = sinx的圖像，其中 0 ? x ? 2?y = sinx的圖像，其中 0 ? x ? 2?5.4 三角函數的圖像及其方程5.4 三角函數的圖像及其方程y = sinx的圖像，其中 0 ? x ? 2?5.4 三角函數的圖像及其方程y = cosx的圖像，其中 0 ? x ? 2?y = cosx的圖像，其中 0 ? x ? 2?5.4 三角函數的圖像及其方程y = cosx的圖像，其中 0 ? x ? 2?5.4 三角函數的圖像及其方程5.4 三角函數的圖像及其方程y = tanx的圖像，其中 0 ? x ? 2?5.4 三角函數的圖像及其方程y = tanx的圖像，其中 0 ? x ? 2?5.4 三角函數的圖像及其方程y = tanx的圖像，其中 0 ? x ? 2?注意：虛線 及 　不會與 的圖像相交解：例 5.145.4 三角函數的圖像及其方程 解：例 5.15 5.4 三角函數的圖像及其方程解：例 5.165.4 三角函數的圖像及其方程 解：例 5.175.4 三角函數的圖像及其方程解：例 5.185.4 三角函數的圖像及其方程解：例 5.195.5 續三角函數的圖像解：例 5.195.5 續三角函數的圖像解：例 5.205.5 續三角函數的圖像5.5 續三角函數的圖像y = Asinx的圖像 (A > 0)5.5 續三角函數的圖像y = Asinx的圖像 (A > 0)5.5 續三角函數的圖像y = Asinx的圖像 (A > 0)5.5 續三角函數的圖像y = Asinx的圖像 (A > 0)5.5 續三角函數的圖像y = sin? x的圖像 (? > 0)5.5 續三角函數的圖像y = sin? x的圖像 (? > 0)5.5 續三角函數的圖像y = sin? x的圖像 (? > 0)5.5 續三角函數的圖像y = sin? x的圖像 (? > 0)5.5 續三角函數的圖像y = sin(x +? )的圖像5.5 續三角函數的圖像y = sin(x +? )的圖像5.5 續三角函數的圖像y = sin(x +? )的圖像5.5 續三角函數的圖像y = sin(x +? )的圖像5.5 續三角函數的圖像y = sinx + B的圖像 (B >0)5.5 續三角函數的圖像y = sinx + B的圖像 (B >0)5.5 續三角函數的圖像y = sinx + B的圖像 (B >0)5.5 續三角函數的圖像y = sinx + B的圖像 (B >0)5.5 續三角函數的圖像y = sinx + B的圖像 (B >0)
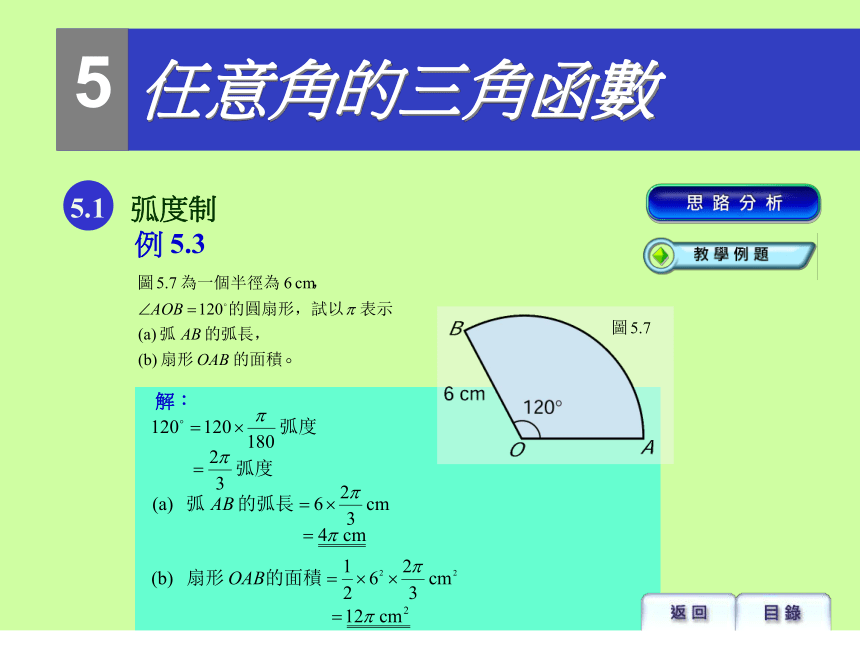
把 120o 轉換為弧度後，便可應用以下公式：5.1 弧度制例 5.3
5.1 弧度制例 5.3
先利用倒數關係，把方程變換為　　　　　　　　A tan2x +B tanx + C = 0 　的形式，然後把所得方程再一次變換為 tanx = k 的形式的三角方程。解：例 5.185.4 三角函數的圖像及其方程解：
例 5.185.4 三角函數的圖像及其方程、、解：