不等式的基本性质2[上学期]
图片预览





文档简介
课件12张PPT。书 山 有 路 勤 为 径,学 海 无 崖 苦 作 舟少 小 不 学 习,老 来 徒 伤 悲 成功=艰苦的劳动+正确的方法+少谈空话天才就是百分之一的灵感,百分之九十九的汗水!天才在于勤奋,努力才能成功!6.1.2不等式的性质教学目标:1.要求学生会用差值比较法比较两个实数的大小.
2.培养学生数形结合的数学思想和灵活应变的解题能力
3.培养学生分类讨论的数学思想和
思考问题严谨周密的习惯.教学重点: 运用作差法比较两个实数的大小.
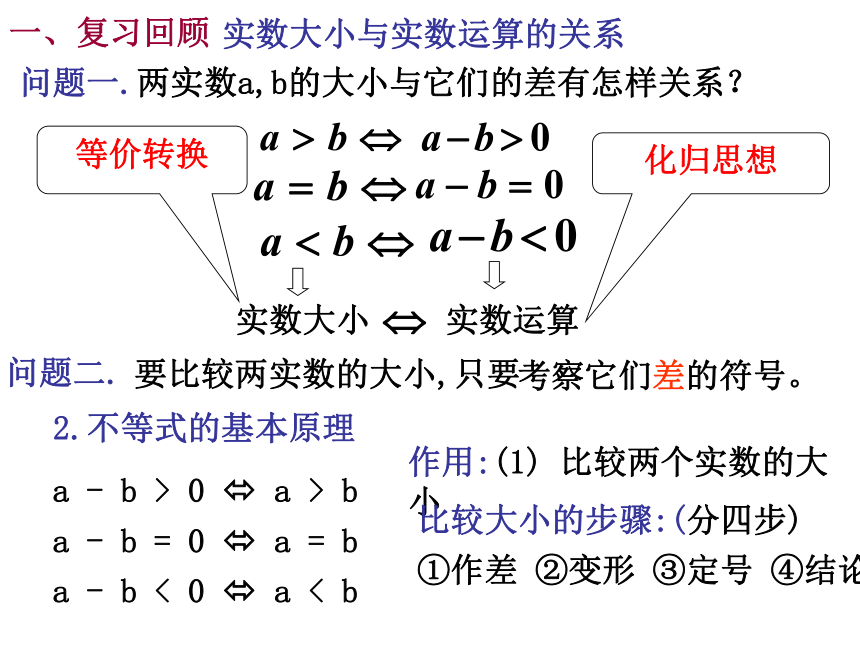
基本步骤:(1)作差 (2)变形 (3)定号 (4)结论教学难点:对命题中?的含义的理解实数大小与实数运算的关系问题一.两实数a,b的大小与它们的差有怎样关系?实数大小实数运算等价转换化归思想一、复习回顾
2.不等式的基本原理a - b > 0 ? a > b
a - b = 0 ? a = b
a - b < 0 ? a < b作用:(1) 比较两个实数的大小比较大小的步骤:(分四步) ①作差 ②变形 ③定号 ④结论.要比较两实数的大小,只要考察它们差的符号。问题二. 问题三:生活中为什么糖水中加的糖越多越甜呢? 转化为数学问题:
若再加m(m>0)克糖,则糖水更甜了,为什么?分析:起初的糖水浓度为 加入m克糖后的糖水浓度为>只要证怎么证呢? >a克糖水中含有b克糖(a>b>0),二、新课引入三.例题讲解例1.已知a>b>0,m>0,试比较 与 的大小③定号. ④结论∵a>b>0,m>0,①作差;比较大小的步骤1.揭示“糖水加糖甜更甜”的数学内涵②变形(关键)技巧:配方(利用非负数性质)或因式分解(确定各因式符号)或通分或有理化等目的:化为常数,积,商,平方和的形式∴a-b>0,a+m>02.真分数的性质:真分数越加越大,越减越小 变式训练③定号.①作差;比较大小的步骤②变形(关键)技巧:配方(利用非负数性质)或因式分解(确定各因式符号)或通分或有理化等.目的:化为常数,积,商,平方和的形式④结论随堂巩固1、已知x>2,则x3+2 2x2+x
2、下列选项正确的是 >C例2.试比较 2x4+1 与 2x3+x2 的大小解: (2x4+1) - (2x3+x2 ) = 2x4+1 - 2x3 _ x2= (2x4 - 2x3 )- (x2 -1) = 2x3 (x -1) - (x -1) (x +1)= (x-1) [2x3 - (x +1) ]= (x-1)[(2x3-2x2) + (2x2-2x) + (x-1)]= (x -1)2 (2x2 + 2x + 1)= (x -1)2 [2 (x + 1/2)2 + 1/2]x∈R ∴ 2 (x + 1/2)2 + 1/2 >0
若 (x -1)2 > 0 即 x≠1 则 2x4+1 > 2x3+x2
若 (x -1)2 = 0 即 x =1 则 2x4+1 = 2x3+x21.配方必不可少三.例题讲解2. 分类讨论三.课堂练习:1.用不等号填空≥>(3). a2+b2+3 2(a-b) 2.选择题:
若a<0,-1 A a>ab>ab2 B ab2>ab>a
C ab>a>ab2 D ab>ab2>aD特殊值法2>(1)作差(2)变形(3)定号(4)结论配方法解:当当∴总有提高题:分类讨论四.课堂小结1.不等式的基本原理a - b > 0 ? a > b
a - b = 0 ? a = b
a - b < 0 ? a < b2.作用(1) 比较两个实数的大小③定号.①作差;3.比较大小的步骤②变形(关键)技巧:因式分解,配方,凑成若干个平方和目的:化为常数,积,商,平方和的形式五.课外作业1.同步作业本P1
2.预习下一节④结论
2.培养学生数形结合的数学思想和灵活应变的解题能力
3.培养学生分类讨论的数学思想和
思考问题严谨周密的习惯.教学重点: 运用作差法比较两个实数的大小.
基本步骤:(1)作差 (2)变形 (3)定号 (4)结论教学难点:对命题中?的含义的理解实数大小与实数运算的关系问题一.两实数a,b的大小与它们的差有怎样关系?实数大小实数运算等价转换化归思想一、复习回顾
2.不等式的基本原理a - b > 0 ? a > b
a - b = 0 ? a = b
a - b < 0 ? a < b作用:(1) 比较两个实数的大小比较大小的步骤:(分四步) ①作差 ②变形 ③定号 ④结论.要比较两实数的大小,只要考察它们差的符号。问题二. 问题三:生活中为什么糖水中加的糖越多越甜呢? 转化为数学问题:
若再加m(m>0)克糖,则糖水更甜了,为什么?分析:起初的糖水浓度为 加入m克糖后的糖水浓度为>只要证怎么证呢? >a克糖水中含有b克糖(a>b>0),二、新课引入三.例题讲解例1.已知a>b>0,m>0,试比较 与 的大小③定号. ④结论∵a>b>0,m>0,①作差;比较大小的步骤1.揭示“糖水加糖甜更甜”的数学内涵②变形(关键)技巧:配方(利用非负数性质)或因式分解(确定各因式符号)或通分或有理化等目的:化为常数,积,商,平方和的形式∴a-b>0,a+m>02.真分数的性质:真分数越加越大,越减越小 变式训练③定号.①作差;比较大小的步骤②变形(关键)技巧:配方(利用非负数性质)或因式分解(确定各因式符号)或通分或有理化等.目的:化为常数,积,商,平方和的形式④结论随堂巩固1、已知x>2,则x3+2 2x2+x
2、下列选项正确的是 >C例2.试比较 2x4+1 与 2x3+x2 的大小解: (2x4+1) - (2x3+x2 ) = 2x4+1 - 2x3 _ x2= (2x4 - 2x3 )- (x2 -1) = 2x3 (x -1) - (x -1) (x +1)= (x-1) [2x3 - (x +1) ]= (x-1)[(2x3-2x2) + (2x2-2x) + (x-1)]= (x -1)2 (2x2 + 2x + 1)= (x -1)2 [2 (x + 1/2)2 + 1/2]x∈R ∴ 2 (x + 1/2)2 + 1/2 >0
若 (x -1)2 > 0 即 x≠1 则 2x4+1 > 2x3+x2
若 (x -1)2 = 0 即 x =1 则 2x4+1 = 2x3+x21.配方必不可少三.例题讲解2. 分类讨论三.课堂练习:1.用不等号填空≥>(3). a2+b2+3 2(a-b) 2.选择题:
若a<0,-1
C ab>a>ab2 D ab>ab2>aD特殊值法2>(1)作差(2)变形(3)定号(4)结论配方法解:当当∴总有提高题:分类讨论四.课堂小结1.不等式的基本原理a - b > 0 ? a > b
a - b = 0 ? a = b
a - b < 0 ? a < b2.作用(1) 比较两个实数的大小③定号.①作差;3.比较大小的步骤②变形(关键)技巧:因式分解,配方,凑成若干个平方和目的:化为常数,积,商,平方和的形式五.课外作业1.同步作业本P1
2.预习下一节④结论
