第四章 几何图形的初步 全章总复习 课件(共38张PPT)
文档属性
| 名称 | 第四章 几何图形的初步 全章总复习 课件(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 06:45:59 | ||
图片预览









文档简介
(共38张PPT)
第四章 几何图形初步
全章总复习
人教版七年级上册
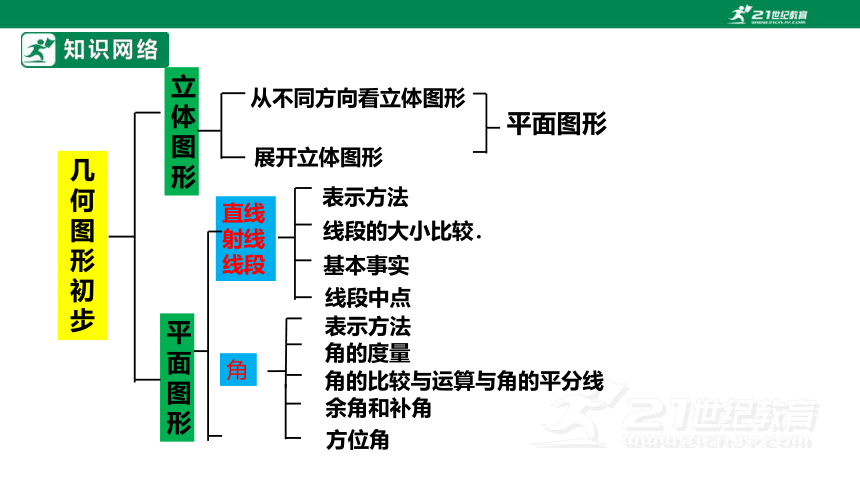
知识网络
几何图形初步
立体图形
平面图形
展开立体图形
从不同方向看立体图形
表示方法
线段的大小比较.
基本事实
线段中点
表示方法
方位角
余角和补角
角的比较与运算与角的平分线
角的度量
平面图形
直线射线线段
角
新知导入
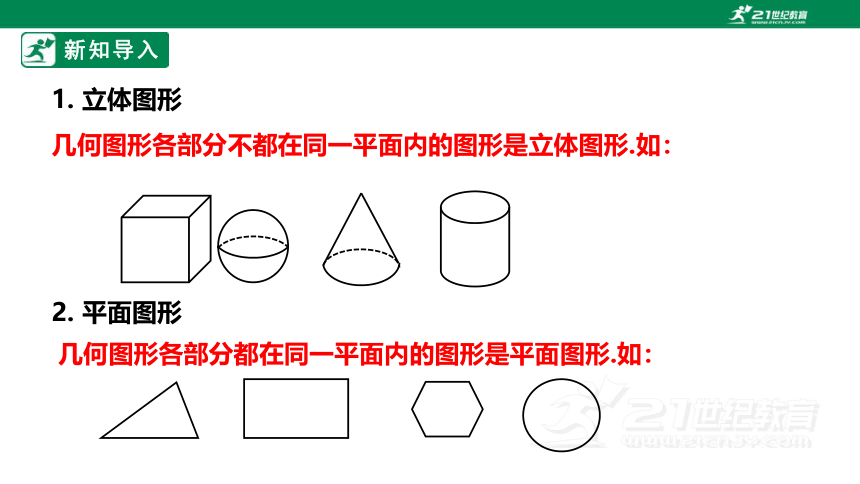
1. 立体图形
几何图形各部分不都在同一平面内的图形是立体图形.如:
几何图形各部分都在同一平面内的图形是平面图形.如:
2. 平面图形
新知讲解
3.立体图形与平面图形的相互转化.
(1).从不同方向看:从 看、从 看、从 看.
正面
左面
上面
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的展开图.
(2)立体图形的展开
新知讲解
4.点、线、面、体
(1).点、线、面、体组成几何图形,点是构成图形的基本元 素.
(2).点、线、面、体之间有如图所示的联系:
点 线 面 体
动
交
动
交
动
(由面包围而成)
新知讲解
5.线段、射线和直线的表示:
直线AB或直线
●
●
A
B
A
O
●
●
射线OA或射线
●
●
A
B
线段AB或线段
新知讲解
常用两种方法,一种是度量法;一种是叠合法.
6.线段的比较长短:
7.两个的基本事实
②直线的基本事实:两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
①直线的基本事实:经过两点有一条直线,并且只有一条直线.
简单说成:两点确定一条直线.
新知讲解
A
B
C
符号语言:AB =AC+BC.
符号语言: BC =AB-AC.
8.线段的和差:
图中共有三条不同的线段,它们和差关系如下:
符号语言: AC=AB-BC.
新知讲解
∴AC=BC= AB
如图,把一条线段分成相等的两条线段的点叫做这条线段的中点.
●
B
A
C
中点
∵C是AB的中点
几何语言:
反之也成立:
∴ C是AB的中点.
9. 线段的中点
∵ AC=BC= AB
连接两点间的线段的长度,叫做这两点的距离.
10.两点的距离:
新知讲解
静态:角是由两条具有公共端点的射线组成的.
动态:角也可以看作由一条射线绕着它的端点旋转而形成的图形.
11.角的定义及表示:
(1).角的两种定义
(2).角的表示方法
①.大写英文字母
②.数字
③.小写希腊字母
A
B
O
∠AOB或∠O
1
∠
∠
新知讲解
①.角的度、分、秒是60进制的,以度、分、秒为单位的角的度量制,叫做角度制.
12.角的度量及单位换算
②.1周角= ,平角= ,直角= , 1°= , 1′ = .
180°
360°
60′
60″
90°
(1).角的大小比较的两种方法:
②叠合法
①度量法
13.角的比较与运算
(2).角的和差.
新知讲解
或∠AOB=∠BOC= .
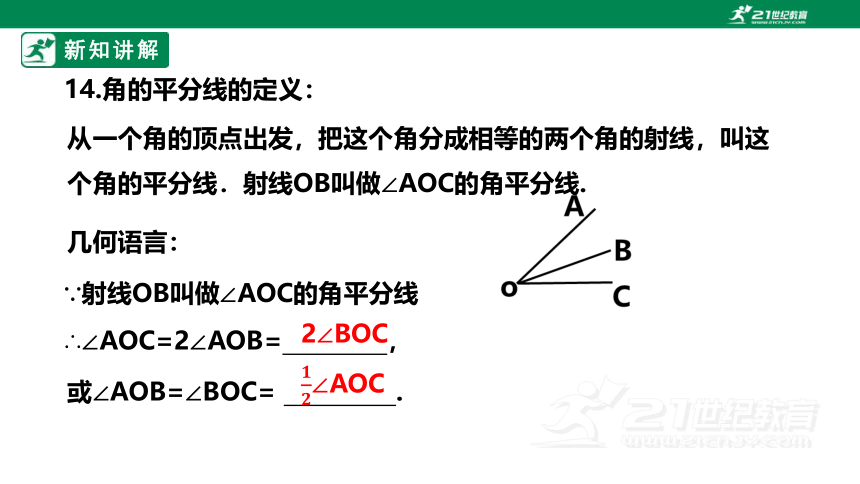
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.射线OB叫做∠AOC的角平分线.
14.角的平分线的定义:
∴∠AOC=2∠AOB= ,
2∠BOC
∵射线OB叫做∠AOC的角平分线
几何语言:
∠AOC
新知讲解
①互为余角:如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
15. 互余和互补
②互为补角:如果两个角的和等于180 (平角),就说这两个角互为补角,即其中每一个角是另一个角的补角.
③性质:同角(或等角)的余角相等;同角(或等角)的补角相等
新知讲解
八大方位:
射线 OQ
16.方位角的定义:
以正北、正南的方向为基准,描述运动的方向,如图OA北偏东30°,OB为南偏东25°,这样的表示方向的角叫做方位角.
西北方向:
西南方向:
东北方向:
东南方向:
正东:
正南:
正西:
正北:
30°
25°
O
B
A
C
D
E
F
M
N
P
Q
射线 ON
射线 OP
射线 OM
射线 OE
射线 OD
射线 OC
射线 OF
典型例题
例1 如图,AD = 40cm,B,C 两点把线段AD分成2:5:3 三部分,M为 AD 的中点,求线段 BM和CM的长.
M
D
A
●
●
●
●
●
B
C
分析:因为B,C 两点把线段AD分成2:5:3 三部分,可设每一份为xcm,则AB=2xcm, BC=5xcm, CD=3xcm,AD=AB+BC+CD,可求得出x.
典型例题
解:设每一份为x cm,则AB= 2x cm, BC = 5x cm,CD= 3x cm,
则 AD = AB+BC+CD =10x cm.
∵M 是 AD 的中点,
∴AM = MD = AD = 20cm.
2x+5x+3x = 40.
解得 x = 4.
故AB= 8cm, BC = 20 cm,CD= 12 cm,
故 BM = AM- AB =20-8 = 12(cm)
CM = MD- CD =20-12 = 8(cm)
典型例题
例2 如图,∠AOB是直角, ON是∠AOC的平分线,OM是∠BOC的平分线.
(1) 当∠AOC=50°时,求∠MON的大小;
典型例题
解:∵∠AOB是直角,∠AOC=50°,
∵ON是∠AOC的平分线,OM是∠BOC的平分线,
∴∠MON=∠COM-∠CON=70°-25°=45°
∠CON= ∠AOC = ×50°= 25°
∴∠COM = ∠BOC = =70°,
∴∠BOC =∠AOB+∠AOC
= 90°+50°=140°,
典型例题
(2) 当∠AOC=α 时, ∠MON等于多少度?
解:∠BOC=∠AOB+∠AOC=90°+α
∵ON是∠AOC的平分线,
∠CON= ∠AOC = α
∴∠COM = ∠BOC = ×(90°+α),
OM是∠BOC的平分线,
∴∠MON=∠COM-∠CON= (90°+α) - α =45°
典型例题
(3) 当锐角∠AOC的大小发生改变时,∠MON的大小也会发生改变吗?为什么?
解:不会发生变化.
由(2)可知∠MON的大小与∠AOC 无关,总是等于∠AOB的一半.
典型例题
例3 若一个角的补角比它的余角的3倍,求这个角的度数.
解:设这个角是x,则它的余角是(90°-x),它的补角是(180°-x), 根据题意得:
180°-x=3(90°-x)
解得x=45°
答:这个角的度数是45°.
课堂演练
1.下列几种图形:①棱锥;②圆;③正方体;④圆柱;⑤球.其中属于立体图形的是( ).
A ①②③ B ①④⑤ C ①③⑤ D ①③④⑤
D
2.圆柱 、圆椎 、球 、圆是平面图形的是( ).
A 圆柱 B 圆椎 C 球 D 圆
3.一个立体图形从正面看、从左面看、从上面看得到的图形是圆,则这个立体图形是( ).
A 正方体 B 球 C 圆锥 D 圆柱
B
D
课堂演练
4.“汽车的雨刷在挡风玻璃上画出一个扇面”可以说是( )
A. 面与面交于线 B. 点动成线 C. 面动成体 D. 线动成面
5.下列哪个图形不可能是正方体的表面展开图( )
A B C D
D
A
课堂演练
6.下列语句正确的是( )
A. 延长线段AB到C , 使BC=AC
B. 反向延长线段AB , 得到射线BA
C. 取射线AB的中点
D. 连接A、B两点,使线段AB过点C
B
课堂演练
7.如图,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是( )
两点之间,线段最短 B. 两点确定一条直线
C. 垂线段最短 D. 三角形两边之和大于第三边
B
课堂演练
8. 下列生活现象,可以用基本事实“两点之间,线段最短”解释的是( )
A. 汽车的雨刮器把玻璃上的水刷干净
B. 开山挖隧道,把上坡下坡的盘山公路改为平直的隧道
C. 公园的喷泉中,喷水龙头喷出的圆形水面
D. 建筑工人通过在两个柱子之间拉一条绳子砌墙
B
课堂演练
9. 若数轴上点A表示的数为-2 , 且点A和点B的距离为3,则点B表示的数是( )
-5 B. 1 C. -2或3 D. -5或1
10. 如图,已知点C是线段OA的中点,点B在线段AC上,点D是线段OB的中点,若线段OA=20cm , 线段OB=12cm , 则线段CD的长度为( )
A. 3cm B. 4cm C. 4.5cm D. 5cm
D
B
课堂演练
11. 某测绘兴趣小组用测绘装置对一建筑的位置进行测量,测量前指针指向北偏东38°,测量后指针顺时针旋转了1/4周,则此时指针指向为( )
北偏西52°
B. 南偏东52°
C. 西偏南42°
D. 东偏北42°
B
课堂演练
12. 将一副直角三角尺按如图所示的不同方式摆放,则图中∠α与∠β不一定相等的是( )
A B
C D
B
13. 如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
A. 2对 B. 3对 C. 4对 D. 5对
14. 如果一个角的余角是60° ,那么这个角的补角的度数是( )
A. 150° B. 140° C. 120° D. 30°
课堂演练
C
A
课堂演练
15. 棋盘上有黑、白两色棋子若干,如果两颗棋子连成的直线上只有颜色相同的棋子,我们就称“同棋共线”.右图中“同棋共线”的直线共有( )
A. 8条 B. 10条 C. 12条 D. 16条
B
课堂演练
16. 若一个角比它的补角大20°,求这个角的度数.
解:设这个角为x,则这个角的补角为(180﹣x),那么
解得x=100°
180°﹣x=x﹣20°,
答:这个角的度数100°.
课堂演练
17. 如图,已知AC=12,AB=8,点D为线段AC的中点,求线段BD的长度.
解:因为AC=12,点D为线段AC的中点,
所以BD=AB-AD=8-6=2.
因为AB=8,
所以AD= AC=6
答:线段BD的长度2.
课堂演练
18. 如图,已知 O 为直线 AB 上一点,过点 O 向直线 AB 上方引三条射线 OC 、 OD 、 OE ,且 OC 平分 ∠AOD , ∠BOE=3∠DOE , ∠COE= 90° ,求 ∠BOE 的度数
解:设∠1=x,根据题意得到下图,则∠2=3∠1=3x
∵∠COE=∠1+∠3=70°
∴∠3=(70-x)
∵OC平分∠AOD,
∴∠4=∠3=(70-x)
∵∠1+∠2+∠3+∠4=180°
∴ x+3x+(70-x)+(70-x)=180°
解得:x=20
∴∠2=3x=60°
∴∠BOE的度数为60°.
课堂演练
19. 如图,点O在直线AB上,∠COE是直角,OF平分∠AOE , ∠COF=30° , 求∠EOB的大小.
解:是直角
,
∵OF平分∠
作业布置
复习题4
第148页第8题、第149页12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第四章 几何图形初步
全章总复习
人教版七年级上册
知识网络
几何图形初步
立体图形
平面图形
展开立体图形
从不同方向看立体图形
表示方法
线段的大小比较.
基本事实
线段中点
表示方法
方位角
余角和补角
角的比较与运算与角的平分线
角的度量
平面图形
直线射线线段
角
新知导入
1. 立体图形
几何图形各部分不都在同一平面内的图形是立体图形.如:
几何图形各部分都在同一平面内的图形是平面图形.如:
2. 平面图形
新知讲解
3.立体图形与平面图形的相互转化.
(1).从不同方向看:从 看、从 看、从 看.
正面
左面
上面
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的展开图.
(2)立体图形的展开
新知讲解
4.点、线、面、体
(1).点、线、面、体组成几何图形,点是构成图形的基本元 素.
(2).点、线、面、体之间有如图所示的联系:
点 线 面 体
动
交
动
交
动
(由面包围而成)
新知讲解
5.线段、射线和直线的表示:
直线AB或直线
●
●
A
B
A
O
●
●
射线OA或射线
●
●
A
B
线段AB或线段
新知讲解
常用两种方法,一种是度量法;一种是叠合法.
6.线段的比较长短:
7.两个的基本事实
②直线的基本事实:两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
①直线的基本事实:经过两点有一条直线,并且只有一条直线.
简单说成:两点确定一条直线.
新知讲解
A
B
C
符号语言:AB =AC+BC.
符号语言: BC =AB-AC.
8.线段的和差:
图中共有三条不同的线段,它们和差关系如下:
符号语言: AC=AB-BC.
新知讲解
∴AC=BC= AB
如图,把一条线段分成相等的两条线段的点叫做这条线段的中点.
●
B
A
C
中点
∵C是AB的中点
几何语言:
反之也成立:
∴ C是AB的中点.
9. 线段的中点
∵ AC=BC= AB
连接两点间的线段的长度,叫做这两点的距离.
10.两点的距离:
新知讲解
静态:角是由两条具有公共端点的射线组成的.
动态:角也可以看作由一条射线绕着它的端点旋转而形成的图形.
11.角的定义及表示:
(1).角的两种定义
(2).角的表示方法
①.大写英文字母
②.数字
③.小写希腊字母
A
B
O
∠AOB或∠O
1
∠
∠
新知讲解
①.角的度、分、秒是60进制的,以度、分、秒为单位的角的度量制,叫做角度制.
12.角的度量及单位换算
②.1周角= ,平角= ,直角= , 1°= , 1′ = .
180°
360°
60′
60″
90°
(1).角的大小比较的两种方法:
②叠合法
①度量法
13.角的比较与运算
(2).角的和差.
新知讲解
或∠AOB=∠BOC= .
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.射线OB叫做∠AOC的角平分线.
14.角的平分线的定义:
∴∠AOC=2∠AOB= ,
2∠BOC
∵射线OB叫做∠AOC的角平分线
几何语言:
∠AOC
新知讲解
①互为余角:如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
15. 互余和互补
②互为补角:如果两个角的和等于180 (平角),就说这两个角互为补角,即其中每一个角是另一个角的补角.
③性质:同角(或等角)的余角相等;同角(或等角)的补角相等
新知讲解
八大方位:
射线 OQ
16.方位角的定义:
以正北、正南的方向为基准,描述运动的方向,如图OA北偏东30°,OB为南偏东25°,这样的表示方向的角叫做方位角.
西北方向:
西南方向:
东北方向:
东南方向:
正东:
正南:
正西:
正北:
30°
25°
O
B
A
C
D
E
F
M
N
P
Q
射线 ON
射线 OP
射线 OM
射线 OE
射线 OD
射线 OC
射线 OF
典型例题
例1 如图,AD = 40cm,B,C 两点把线段AD分成2:5:3 三部分,M为 AD 的中点,求线段 BM和CM的长.
M
D
A
●
●
●
●
●
B
C
分析:因为B,C 两点把线段AD分成2:5:3 三部分,可设每一份为xcm,则AB=2xcm, BC=5xcm, CD=3xcm,AD=AB+BC+CD,可求得出x.
典型例题
解:设每一份为x cm,则AB= 2x cm, BC = 5x cm,CD= 3x cm,
则 AD = AB+BC+CD =10x cm.
∵M 是 AD 的中点,
∴AM = MD = AD = 20cm.
2x+5x+3x = 40.
解得 x = 4.
故AB= 8cm, BC = 20 cm,CD= 12 cm,
故 BM = AM- AB =20-8 = 12(cm)
CM = MD- CD =20-12 = 8(cm)
典型例题
例2 如图,∠AOB是直角, ON是∠AOC的平分线,OM是∠BOC的平分线.
(1) 当∠AOC=50°时,求∠MON的大小;
典型例题
解:∵∠AOB是直角,∠AOC=50°,
∵ON是∠AOC的平分线,OM是∠BOC的平分线,
∴∠MON=∠COM-∠CON=70°-25°=45°
∠CON= ∠AOC = ×50°= 25°
∴∠COM = ∠BOC = =70°,
∴∠BOC =∠AOB+∠AOC
= 90°+50°=140°,
典型例题
(2) 当∠AOC=α 时, ∠MON等于多少度?
解:∠BOC=∠AOB+∠AOC=90°+α
∵ON是∠AOC的平分线,
∠CON= ∠AOC = α
∴∠COM = ∠BOC = ×(90°+α),
OM是∠BOC的平分线,
∴∠MON=∠COM-∠CON= (90°+α) - α =45°
典型例题
(3) 当锐角∠AOC的大小发生改变时,∠MON的大小也会发生改变吗?为什么?
解:不会发生变化.
由(2)可知∠MON的大小与∠AOC 无关,总是等于∠AOB的一半.
典型例题
例3 若一个角的补角比它的余角的3倍,求这个角的度数.
解:设这个角是x,则它的余角是(90°-x),它的补角是(180°-x), 根据题意得:
180°-x=3(90°-x)
解得x=45°
答:这个角的度数是45°.
课堂演练
1.下列几种图形:①棱锥;②圆;③正方体;④圆柱;⑤球.其中属于立体图形的是( ).
A ①②③ B ①④⑤ C ①③⑤ D ①③④⑤
D
2.圆柱 、圆椎 、球 、圆是平面图形的是( ).
A 圆柱 B 圆椎 C 球 D 圆
3.一个立体图形从正面看、从左面看、从上面看得到的图形是圆,则这个立体图形是( ).
A 正方体 B 球 C 圆锥 D 圆柱
B
D
课堂演练
4.“汽车的雨刷在挡风玻璃上画出一个扇面”可以说是( )
A. 面与面交于线 B. 点动成线 C. 面动成体 D. 线动成面
5.下列哪个图形不可能是正方体的表面展开图( )
A B C D
D
A
课堂演练
6.下列语句正确的是( )
A. 延长线段AB到C , 使BC=AC
B. 反向延长线段AB , 得到射线BA
C. 取射线AB的中点
D. 连接A、B两点,使线段AB过点C
B
课堂演练
7.如图,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是( )
两点之间,线段最短 B. 两点确定一条直线
C. 垂线段最短 D. 三角形两边之和大于第三边
B
课堂演练
8. 下列生活现象,可以用基本事实“两点之间,线段最短”解释的是( )
A. 汽车的雨刮器把玻璃上的水刷干净
B. 开山挖隧道,把上坡下坡的盘山公路改为平直的隧道
C. 公园的喷泉中,喷水龙头喷出的圆形水面
D. 建筑工人通过在两个柱子之间拉一条绳子砌墙
B
课堂演练
9. 若数轴上点A表示的数为-2 , 且点A和点B的距离为3,则点B表示的数是( )
-5 B. 1 C. -2或3 D. -5或1
10. 如图,已知点C是线段OA的中点,点B在线段AC上,点D是线段OB的中点,若线段OA=20cm , 线段OB=12cm , 则线段CD的长度为( )
A. 3cm B. 4cm C. 4.5cm D. 5cm
D
B
课堂演练
11. 某测绘兴趣小组用测绘装置对一建筑的位置进行测量,测量前指针指向北偏东38°,测量后指针顺时针旋转了1/4周,则此时指针指向为( )
北偏西52°
B. 南偏东52°
C. 西偏南42°
D. 东偏北42°
B
课堂演练
12. 将一副直角三角尺按如图所示的不同方式摆放,则图中∠α与∠β不一定相等的是( )
A B
C D
B
13. 如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
A. 2对 B. 3对 C. 4对 D. 5对
14. 如果一个角的余角是60° ,那么这个角的补角的度数是( )
A. 150° B. 140° C. 120° D. 30°
课堂演练
C
A
课堂演练
15. 棋盘上有黑、白两色棋子若干,如果两颗棋子连成的直线上只有颜色相同的棋子,我们就称“同棋共线”.右图中“同棋共线”的直线共有( )
A. 8条 B. 10条 C. 12条 D. 16条
B
课堂演练
16. 若一个角比它的补角大20°,求这个角的度数.
解:设这个角为x,则这个角的补角为(180﹣x),那么
解得x=100°
180°﹣x=x﹣20°,
答:这个角的度数100°.
课堂演练
17. 如图,已知AC=12,AB=8,点D为线段AC的中点,求线段BD的长度.
解:因为AC=12,点D为线段AC的中点,
所以BD=AB-AD=8-6=2.
因为AB=8,
所以AD= AC=6
答:线段BD的长度2.
课堂演练
18. 如图,已知 O 为直线 AB 上一点,过点 O 向直线 AB 上方引三条射线 OC 、 OD 、 OE ,且 OC 平分 ∠AOD , ∠BOE=3∠DOE , ∠COE= 90° ,求 ∠BOE 的度数
解:设∠1=x,根据题意得到下图,则∠2=3∠1=3x
∵∠COE=∠1+∠3=70°
∴∠3=(70-x)
∵OC平分∠AOD,
∴∠4=∠3=(70-x)
∵∠1+∠2+∠3+∠4=180°
∴ x+3x+(70-x)+(70-x)=180°
解得:x=20
∴∠2=3x=60°
∴∠BOE的度数为60°.
课堂演练
19. 如图,点O在直线AB上,∠COE是直角,OF平分∠AOE , ∠COF=30° , 求∠EOB的大小.
解:是直角
,
∵OF平分∠
作业布置
复习题4
第148页第8题、第149页12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
