不等式的证明—构造法[上学期]

课件11张PPT。 f(x)=x+　　(a>0)的单调性f(x)在〔√a，+∞)、(-∞，-√ a]上为增函数 f(x)在〔- √a，0)、(0，√a]上为减函数ax复习回顾构造法希望你喜欢，大力提升创造性 51理解掌握构造法的基本原理和思路
2 通过学习进一步提高灵活应变的解题能力学习目标例1、求证： 证：设 则
令：3≤t1∴y= 〔3，+∞)上单调递增=t+1
t x2+10
√x2+9≥f(3)=10
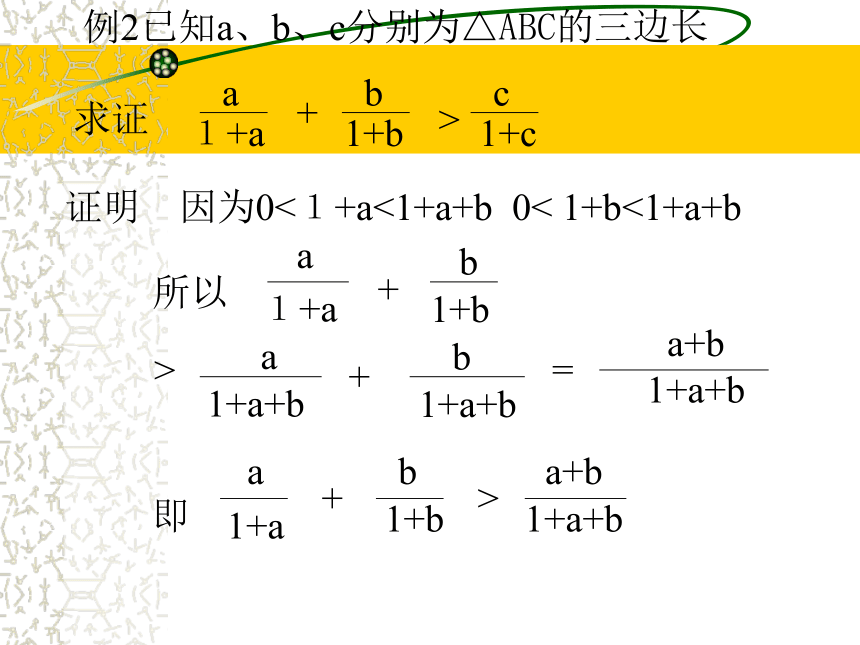
3 例2已知a、b、c分别为△ABC的三边长
求证a１+a+b1+b> c1+c证明　因为0<１+a<1+a+b 0< 1+b<1+a+b所以a１+a+b1+b>a1+a+b+b1+a+b=a+b1+a+b即a1+a+b1+b>a+b1+a+b令f(x)=x1+x则f(x)=1-11+x在〔0，+∞)上为增函数因为a+b> c 所以 f(a+b)> f(c)即a+b1+a+b> c1+c所以a1+a+b1+b>c1+c例3.证明证明:设则(1)当y≠1时,由x(2)当y=1时,由(1-y) +x+1-y=0,得x=0.
而且x=0是函数的定义域中的一个值,所以y=1是它值域中的一个值.
由(1)(2)得
例4.已知实数a, b, c，满足a + b + c = 0和abc = 2，求证：a, b, c中至少有一个不小于2。
证：由题设：显然a, b, c中必有一个正数， 不妨设a > 0， 则∴即：a≥2b、c是方程的两根
例5已知a、b、c、d∈R　求证〡ac+bd〡≤ √a2+b2√c2+d2证明　令　m =(a，b) n =(c，d).　则有m.n =〡m〡.〡n〡cosθ〡m.n〡≤〡m〡.〡n〡∵〡m. n 〡=ac+bd〡 m〡 = √a2+b2 〡 n〡= √c2+d2∴〡ac+bd〡 ≤√ a2+b2 .√ c2+d2练习：已知abc是⊿ABC的三条边m是正数

求证 a b c
a+m b+m c+m+＞证明　因为0aa+b+m+ba+b+m=a+ba+b+m即aa+m+bb+m>a+ba+b+m令f(x)=xx+m则f(x)=1-mx+m在﹙-m，+∞)上为增函数因为a+b> c 所以 f(a+b)> f(c)即a+ba+b+m> cC+m所以aa+m+bb+m>cc+m