一元二次不等式的解法[上学期]
文档属性
| 名称 | 一元二次不等式的解法[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 127.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-09-26 18:09:00 | ||
图片预览




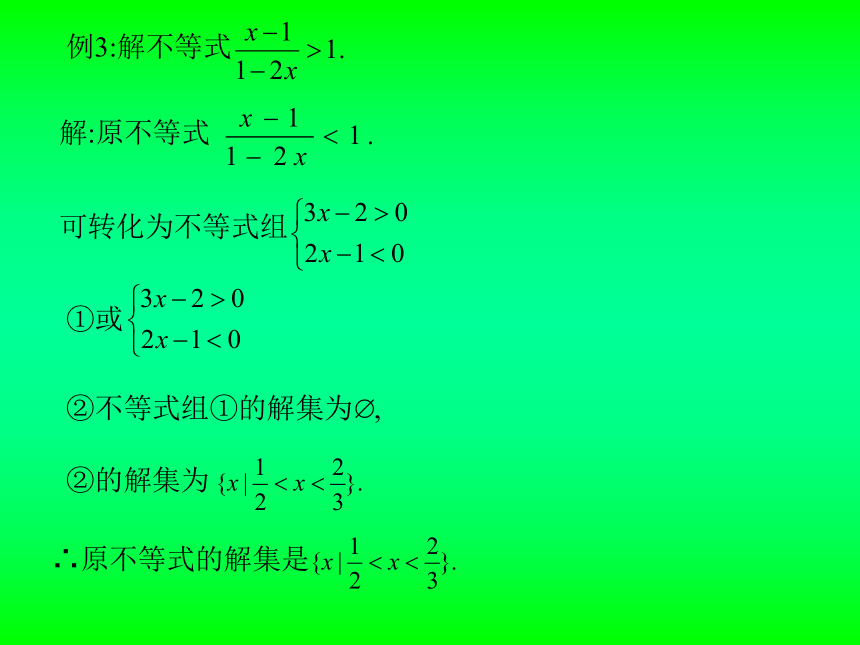

文档简介
课件13张PPT。1.5一元二次不等式的解法授课教师:谢大选例1:解下列不等式.(1)-2x2 + x + <0; (2)x2>2x-3;(3)3x2 + 5≤=3x.解:(1)原不等式变形为2x2-x- >0,解方程2x2-x- = 0得x1 = , x2 = ,
∴原不等式的解集为{x|x< 或x> }.(2)原不等式变形为x2 -2x + 3>0,解方程x2-2x+3 = 0, 因为△= 4-12 = -8<0,所以原方程无实数根,所以原不等式的解集是{x|x∈R}.(3)原不等式变形为3x2 -3x + 5≤0.解方程3x2 -3x + 5≤0.因为△= 9-60 <0,所以原方程无实数根,所以原不等式的解集为 .思维发散: 解不等式(1)1<(x-3)2≤2;(2)x2-2|x|-15≥0.略解: (1)原不等式可化为不等式组:解得∴原不等式的解集为{x|3 ≤x<2或40. 解:原不等式整理得(x-a)(x-1)>0.∴原不等式可转化为下面两个不等式组来解:①或②即∴当a>1,原不等式的解集为{x|x>a或x<1};当a<1时,原不等式的解集为{x|x>1或xm值的取值集合.(1)1根小于0,另一根大于2;(2)1根在0与1之间,1根在1与2之间;(3)2根都大于-5.解:设二次函数y = x2-mx-m + 3.(1)若1根小于0,另1根大于2,由图1知:x = 0时,y<0;x = 2时, y<0,即∴m > 3.(2)1根在0与1之间,另一根在1与2之间,由图2知:x= 0时,y>0;x=1时,y<0;x=2时,y>0.∴20,且对称轴x= >-5,且△≥0,∴-6≤m≤2思维发散:不等式x2-2mx-1>0对一切1≤x≤3都成立,求m的取值集合.略解:本题只要求{x|1≤x≤3} {x|x2-2mx-1>0}即可,借助二次函数图像列出m应满足的不等式.∵△=4m2+4>0,∴x2-2mx-1=0必有两根,故两根x1,x2要么都大于3,要么都小于1,
又∵ x1,x2=-1, ∴ x1,x2都只能小于1, ∴x=1时,y>0.∴1-2m-1>0, ∴m<0.例10:已知三个不等式:x2-4x+3<0①x2-6x+8<0②2x2-6x+8<0③2x2-9x+a<0④要使满足不等式①, ②的所有x的值也满足不等式③,求a的取值范围.解:由不等式①, ②组成的不等式组本题相当于:满足2y<0,由于x= 介于2和3之间,则有x=2时,y≤0,且x=3时, y≤0,即a的取值范围是a≤9.
∴原不等式的解集为{x|x< 或x> }.(2)原不等式变形为x2 -2x + 3>0,解方程x2-2x+3 = 0, 因为△= 4-12 = -8<0,所以原方程无实数根,所以原不等式的解集是{x|x∈R}.(3)原不等式变形为3x2 -3x + 5≤0.解方程3x2 -3x + 5≤0.因为△= 9-60 <0,所以原方程无实数根,所以原不等式的解集为 .思维发散: 解不等式(1)1<(x-3)2≤2;(2)x2-2|x|-15≥0.略解: (1)原不等式可化为不等式组:解得∴原不等式的解集为{x|3 ≤x<2或4
又∵ x1,x2=-1, ∴ x1,x2都只能小于1, ∴x=1时,y>0.∴1-2m-1>0, ∴m<0.例10:已知三个不等式:x2-4x+3<0①x2-6x+8<0②2x2-6x+8<0③2x2-9x+a<0④要使满足不等式①, ②的所有x的值也满足不等式③,求a的取值范围.解:由不等式①, ②组成的不等式组本题相当于:满足2
