一元二次不等式的解法1(高)[上学期]
文档属性
| 名称 | 一元二次不等式的解法1(高)[上学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 34.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-29 00:00:00 | ||
图片预览






文档简介
课件17张PPT。一元二次不等式的解法
(一)界首中学 数学课件问题:(1)如何解一元二次方程
(2)二次函数 的图象是
什么曲线?
(3)一元二次方程 的
解与二次函数 的图象
有什么联系?一元二次方程 的解实
际上就是二次函数
与x轴交点的横坐标。下面我们来研究如何应用二次函数的图象
来解一元二次不等式。首先,我们可以把任何一个一元二次
不等式转化为下列四种形式中的一种:以上四个不等式中我们规定了
如果题目中给出的不等式中二次项系
数小于0,哪怎么办呢?对了,我们只要在不等式两边同乘-1,
然后把不等式的方向改变一下,就可
化为以上四种形式中的一种。下面我们就利用二次函数的图象来解
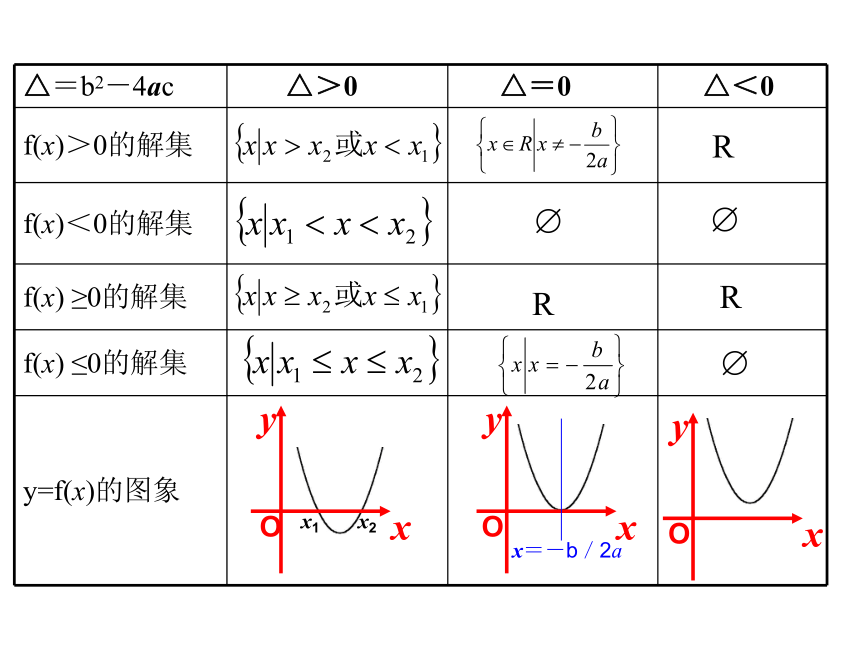
以上4个不等式。设f(x)=ax2+bx+c (a>0),且设方程f(x)=0在△>0时的两个根分别是x1、x2,且x1<x2。下面我们一起来完成下表:?R R ? R?填写上表的依据是二次函数的图象,这实际上是一种数形结合的思想。由此我们可以得出解一元二次不等式的一般步骤:(1)把所给不等式化为四种标准形式之一;(2)判断所对应二次方程的根的情况;若
有根,则求出其根。(3)画出所对应的二次函数的图象;(4)根据图象写出不等式的解集。例1:解下列不等式
( 1) 2x2-3x-2>0
解:令2x2-3x-2=0
∵△=9+16=25>0
方程2x2-3x-2=0的解是x1=-1/2 x2=2
∴原不等式的解集为{x|x<-1/2或x>2}
(2) -3x2+6x>2
解: 3x2-6x+2<0
令 3x2-6x+2=0
∵△=36-24=12>0
方程3x2-6x+2=0的解是x1=1-√3/3 , x2=1+√3/3,
∴原不等式的解集为{x|1-√3/3?
-0.52
(3)4x2+4x+1<0 解: 4x2+4x+1 =0
∵⊿=0
方程的根为x1=x2=-1/2
∴原不等式的解集为?
(4)x2-3x+5>0
解:令x2-3x+5 =0
∵⊿=9-20<0
∴原不等式的解集为R
0.5 (3) 4x2-4x+1>0
解:令4x2-4x+1=0
∵△=16-16=0
方程4x2-4x+1=0的解是x1=x2=1/2
∴原不等式的解集为{x|x≠1/2}
(4)- x2+2x-3>0
解: x2-2x+3<0
令x2-2x+3=0
∵△=4-12= -8<0
方程2x2-3x-2=0无实数根
∴原不等式的解集为ф0.52.解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0) 的步骤是: (1)化成标准形式 ax2+bx+c>0(a>0)
ax2+bx+c<0 (a>0)
(2)求⊿,并求出方程ax2+bx+c=0 的实根
(3)根据图象写出解集(可记忆为:大于取
两边,小于取中间) 课堂练习1.解下列不等式
(1)3x2-7x+2<0
?
?
解:令3x2-7x+2=0
∵⊿=49-24=25>0
X1=1/3,x2=2
∴原不等式的解集为
﹛x|1/3(2)–6x2-x+2 ≦0
解: 6x2+x-2 ≧ 0
∵⊿=1+48=49>0
X1= -2/3,x2=1/2
∴原不等式的解集为:{x|x≦-2/3或x≧1/2 }1/32
(3)4x2+4x+1<0 解:4x2+4x+1=0
∵⊿=0
方程的根为x1=x2=-1/2
∴原不等式的解集为?
(4)x2-3x+5>0
解:令x2-3x+5=0
∵⊿=9-20<0
∴原不等式的解集为R
0.5例2. 为何值时,函数y=-x2-2x+8 的值等于0,大于0,小于0?解:令- x2-2x+8=0
X2+2x-8=0
X1=-4,x2=2
如图
当x= - 4,2 时y=0
当x<-4或x>2 时y>0
当 –4-42oxy课堂练习2. x是什么实数时,函数y=x2-4x+1的值 (1) 等于0? (2) 是正数? (3) 是负数?
解:令x2-4x+1=0
X1=2-√3, x2=2+√3
∴当x=2- √3, 2+√3 时,y=0
当x<2- √3或x> 2+√3 时,y>0
当2- √3课堂练习3. 是什么实数时, √x2+x-12有意义?
解: x2+x-12≧0
解之得 x≦ - 4或x≧3
∴当x≦ - 4或x≧3时√x2+x-12有意义
本课小节:解一元二次不等式的步骤:
(1)化成标准形式(a>0)
(2)解方程ax2+bx+c=0
(3)由图象写解集
(一)界首中学 数学课件问题:(1)如何解一元二次方程
(2)二次函数 的图象是
什么曲线?
(3)一元二次方程 的
解与二次函数 的图象
有什么联系?一元二次方程 的解实
际上就是二次函数
与x轴交点的横坐标。下面我们来研究如何应用二次函数的图象
来解一元二次不等式。首先,我们可以把任何一个一元二次
不等式转化为下列四种形式中的一种:以上四个不等式中我们规定了
如果题目中给出的不等式中二次项系
数小于0,哪怎么办呢?对了,我们只要在不等式两边同乘-1,
然后把不等式的方向改变一下,就可
化为以上四种形式中的一种。下面我们就利用二次函数的图象来解
以上4个不等式。设f(x)=ax2+bx+c (a>0),且设方程f(x)=0在△>0时的两个根分别是x1、x2,且x1<x2。下面我们一起来完成下表:?R R ? R?填写上表的依据是二次函数的图象,这实际上是一种数形结合的思想。由此我们可以得出解一元二次不等式的一般步骤:(1)把所给不等式化为四种标准形式之一;(2)判断所对应二次方程的根的情况;若
有根,则求出其根。(3)画出所对应的二次函数的图象;(4)根据图象写出不等式的解集。例1:解下列不等式
( 1) 2x2-3x-2>0
解:令2x2-3x-2=0
∵△=9+16=25>0
方程2x2-3x-2=0的解是x1=-1/2 x2=2
∴原不等式的解集为{x|x<-1/2或x>2}
(2) -3x2+6x>2
解: 3x2-6x+2<0
令 3x2-6x+2=0
∵△=36-24=12>0
方程3x2-6x+2=0的解是x1=1-√3/3 , x2=1+√3/3,
∴原不等式的解集为{x|1-√3/3
-0.52
(3)4x2+4x+1<0 解: 4x2+4x+1 =0
∵⊿=0
方程的根为x1=x2=-1/2
∴原不等式的解集为?
(4)x2-3x+5>0
解:令x2-3x+5 =0
∵⊿=9-20<0
∴原不等式的解集为R
0.5 (3) 4x2-4x+1>0
解:令4x2-4x+1=0
∵△=16-16=0
方程4x2-4x+1=0的解是x1=x2=1/2
∴原不等式的解集为{x|x≠1/2}
(4)- x2+2x-3>0
解: x2-2x+3<0
令x2-2x+3=0
∵△=4-12= -8<0
方程2x2-3x-2=0无实数根
∴原不等式的解集为ф0.52.解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0) 的步骤是: (1)化成标准形式 ax2+bx+c>0(a>0)
ax2+bx+c<0 (a>0)
(2)求⊿,并求出方程ax2+bx+c=0 的实根
(3)根据图象写出解集(可记忆为:大于取
两边,小于取中间) 课堂练习1.解下列不等式
(1)3x2-7x+2<0
?
?
解:令3x2-7x+2=0
∵⊿=49-24=25>0
X1=1/3,x2=2
∴原不等式的解集为
﹛x|1/3
解: 6x2+x-2 ≧ 0
∵⊿=1+48=49>0
X1= -2/3,x2=1/2
∴原不等式的解集为:{x|x≦-2/3或x≧1/2 }1/32
(3)4x2+4x+1<0 解:4x2+4x+1=0
∵⊿=0
方程的根为x1=x2=-1/2
∴原不等式的解集为?
(4)x2-3x+5>0
解:令x2-3x+5=0
∵⊿=9-20<0
∴原不等式的解集为R
0.5例2. 为何值时,函数y=-x2-2x+8 的值等于0,大于0,小于0?解:令- x2-2x+8=0
X2+2x-8=0
X1=-4,x2=2
如图
当x= - 4,2 时y=0
当x<-4或x>2 时y>0
当 –4
解:令x2-4x+1=0
X1=2-√3, x2=2+√3
∴当x=2- √3, 2+√3 时,y=0
当x<2- √3或x> 2+√3 时,y>0
当2- √3
解: x2+x-12≧0
解之得 x≦ - 4或x≧3
∴当x≦ - 4或x≧3时√x2+x-12有意义
本课小节:解一元二次不等式的步骤:
(1)化成标准形式(a>0)
(2)解方程ax2+bx+c=0
(3)由图象写解集
