苏教版高中必修一 5.1 函数的概念和图象 课件(共17张PPT)
文档属性
| 名称 | 苏教版高中必修一 5.1 函数的概念和图象 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 21:13:42 | ||
图片预览




文档简介
(共17张PPT)
2.1.2 函数的表示方法
2
温故知新
3
问题1:这三个函数关系分别是用什么形式呈现?
温故知新
4
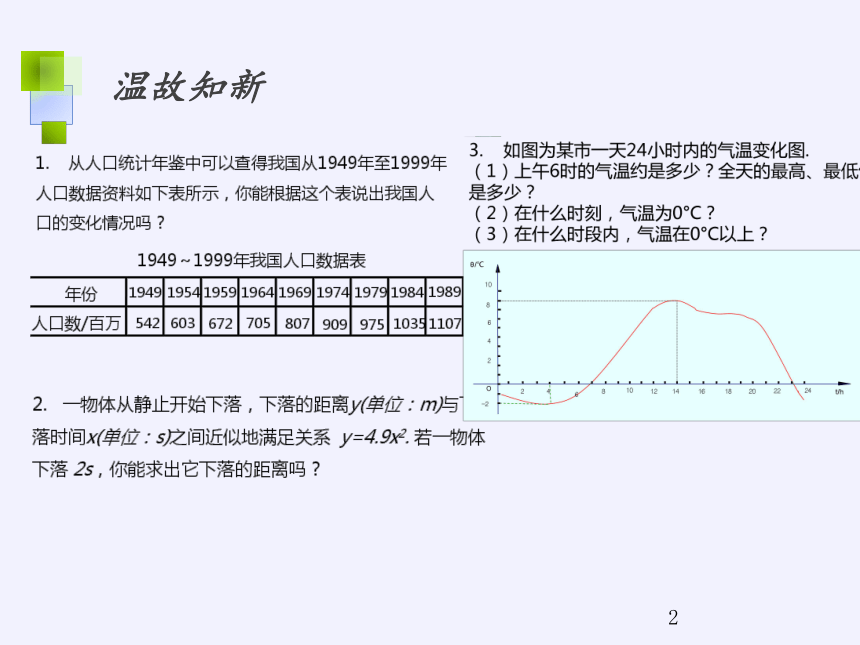
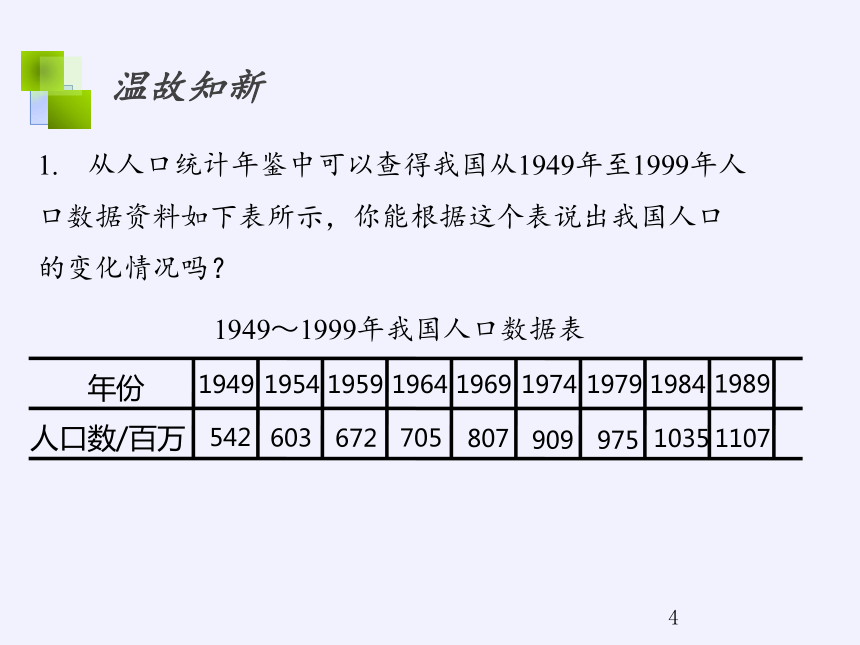
1. 从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料如下表所示,你能根据这个表说出我国人口的变化情况吗?
1949~1999年我国人口数据表
年份
人口数/百万
1949
1954
1959
1964
1969
1974
1979
1984
1989
542
603
672
705
807
1107
1035
975
909
温故知新
5
2. 一物体从静止开始下落,下落的距离y(单位:m)与下落时间x(单位:s)之间近似地满足关系 y=4.9x2. 若一物体下落 2s,你能求出它下落的距离吗?
温故知新
6
t/h
θ/℃
-2
10
8
6
4
2
24
22
20
18
16
14
12
10
8
6
4
2
O
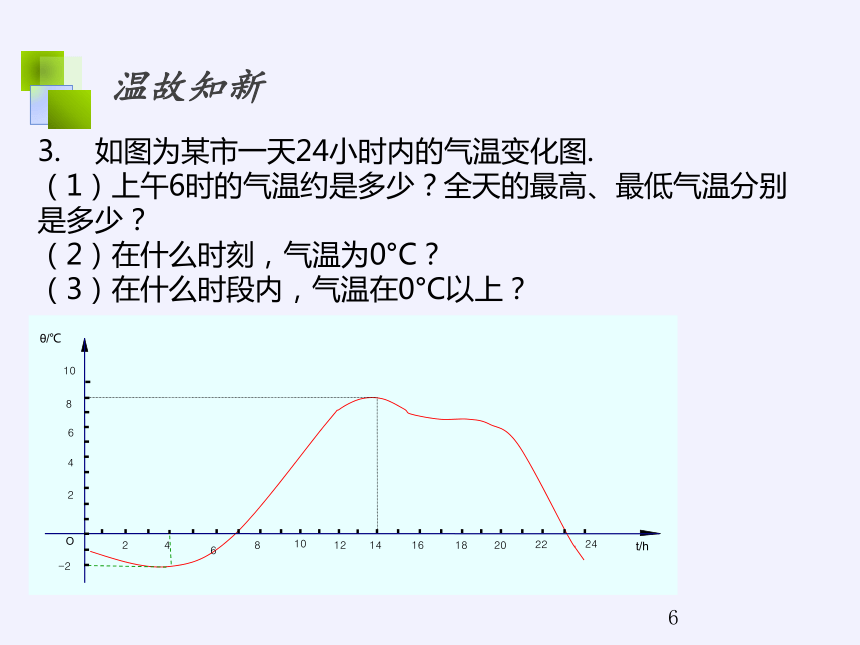
3. 如图为某市一天24小时内的气温变化图.
(1)上午6时的气温约是多少?全天的最高、最低气温分别是多少?
(2)在什么时刻,气温为0°C?
(3)在什么时段内,气温在0°C以上?
温故知新
7
温故知新
问题2:结合三个实例,请你分析这三种表示
方法各自有什么优缺点?
8
1. 从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料如下表所示,你能根据这个表说出我国人口的变化情况吗?
1949~1999年我国人口数据表
年份
人口数/百万
1949
1954
1959
1964
1969
1974
1979
1984
1989
542
603
672
705
807
1107
1035
975
909
温故知新
9
2. 一物体从静止开始下落,下落的距离y(单位:m)与下落时间x(单位:s)之间近似地满足关系 y=4.9x2. 若一物体下落 2s,你能求出它下落的距离吗?
温故知新
10
t/h
θ/℃
-2
10
8
6
4
2
24
22
20
18
16
14
12
10
8
6
4
2
O
3. 如图为某市一天24小时内的气温变化图.
(1)上午6时的气温约是多少?全天的最高、最低气温分别是多少?
(2)在什么时刻,气温为0°C?
(3)在什么时段内,气温在0°C以上?
温故知新
在用解析法表示函数时,一定要写出函数的定义域。
11
例1. 某种笔记本的单价是2元,买x个笔记本(x∈{1,2,3,4}),需要y元,试用三种方法分别表示出x与y的函数关系.
学以致用
注:
12
问题3:还能用 y=2x 表示x与y的函数关系吗?
学以致用
x/个
y/元
1
2
3
4
2
4
4.5
6
13
问题4:初中见过这样的表达式吗?
分段函数
注:(1)是一个函数,而不是几个函数;
(2)定义域是各段定义域的并集,值域是各段值域的并集.
在定义域内不同部分上,有不同的解析式,通常叫做分段函数。
14
例2. 连云港市出租汽车收费标准如下:
在3km以内(含3km)路程按起步价7元收费,在3km以外的路程按2元/km收费. 试写出收费额(单位:元)关于路程(单位:km)的函数解析式,并画出函数图象.
小试牛刀
15
再接再厉
例3. 某质点在30s内运动速度v是时间t的函数,它的图像如图. 试用解析法表示出这个函数,并求出9s时质点的速度.
t/s
v/(cm/s)
0 5 10 15 20 25 30
30
25
20
15
10
5
t∈[0,5)
t∈[5,10)
t∈[10,20)
t∈[20,30].
16
学习目标
正确认识和使用函数的三种表示方法,
了解每种方法的优点和缺点;
求简单分段函数的解析式.
谢 谢
2.1.2 函数的表示方法
2
温故知新
3
问题1:这三个函数关系分别是用什么形式呈现?
温故知新
4
1. 从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料如下表所示,你能根据这个表说出我国人口的变化情况吗?
1949~1999年我国人口数据表
年份
人口数/百万
1949
1954
1959
1964
1969
1974
1979
1984
1989
542
603
672
705
807
1107
1035
975
909
温故知新
5
2. 一物体从静止开始下落,下落的距离y(单位:m)与下落时间x(单位:s)之间近似地满足关系 y=4.9x2. 若一物体下落 2s,你能求出它下落的距离吗?
温故知新
6
t/h
θ/℃
-2
10
8
6
4
2
24
22
20
18
16
14
12
10
8
6
4
2
O
3. 如图为某市一天24小时内的气温变化图.
(1)上午6时的气温约是多少?全天的最高、最低气温分别是多少?
(2)在什么时刻,气温为0°C?
(3)在什么时段内,气温在0°C以上?
温故知新
7
温故知新
问题2:结合三个实例,请你分析这三种表示
方法各自有什么优缺点?
8
1. 从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料如下表所示,你能根据这个表说出我国人口的变化情况吗?
1949~1999年我国人口数据表
年份
人口数/百万
1949
1954
1959
1964
1969
1974
1979
1984
1989
542
603
672
705
807
1107
1035
975
909
温故知新
9
2. 一物体从静止开始下落,下落的距离y(单位:m)与下落时间x(单位:s)之间近似地满足关系 y=4.9x2. 若一物体下落 2s,你能求出它下落的距离吗?
温故知新
10
t/h
θ/℃
-2
10
8
6
4
2
24
22
20
18
16
14
12
10
8
6
4
2
O
3. 如图为某市一天24小时内的气温变化图.
(1)上午6时的气温约是多少?全天的最高、最低气温分别是多少?
(2)在什么时刻,气温为0°C?
(3)在什么时段内,气温在0°C以上?
温故知新
在用解析法表示函数时,一定要写出函数的定义域。
11
例1. 某种笔记本的单价是2元,买x个笔记本(x∈{1,2,3,4}),需要y元,试用三种方法分别表示出x与y的函数关系.
学以致用
注:
12
问题3:还能用 y=2x 表示x与y的函数关系吗?
学以致用
x/个
y/元
1
2
3
4
2
4
4.5
6
13
问题4:初中见过这样的表达式吗?
分段函数
注:(1)是一个函数,而不是几个函数;
(2)定义域是各段定义域的并集,值域是各段值域的并集.
在定义域内不同部分上,有不同的解析式,通常叫做分段函数。
14
例2. 连云港市出租汽车收费标准如下:
在3km以内(含3km)路程按起步价7元收费,在3km以外的路程按2元/km收费. 试写出收费额(单位:元)关于路程(单位:km)的函数解析式,并画出函数图象.
小试牛刀
15
再接再厉
例3. 某质点在30s内运动速度v是时间t的函数,它的图像如图. 试用解析法表示出这个函数,并求出9s时质点的速度.
t/s
v/(cm/s)
0 5 10 15 20 25 30
30
25
20
15
10
5
t∈[0,5)
t∈[5,10)
t∈[10,20)
t∈[20,30].
16
学习目标
正确认识和使用函数的三种表示方法,
了解每种方法的优点和缺点;
求简单分段函数的解析式.
谢 谢
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
