一元二次不等式的解法[上学期]
图片预览



文档简介
课件12张PPT。解一元二次不等式的图象法
xyo引例1. 如何作出一次函数y=2x-7的图象? 令x=0 则y= - 7, 得到点A(0,-7)
令y=0则x=3.5,得到点B(3.5,0)
经过两点A、B作直线m即得y=2x-7的图象,如下图:
o-73.5
(1).根据图象得:
X取___________时,y=0即2x-7=0
X取___________时,y>0即2x-7>0
X取___________时,y<0即2x-7<0xyX=3.5X<3.5X>3.5(2).根据图象得:
不等式2x-7>0的解集_____________
不等式2x-7<0的解集_____________ ﹛x|x<7/2﹜﹛x|x>7/2﹜m 引例2.根据一元二次函数y=x2-x-6的图象回答:
(1).图象与x轴交点的坐标为___________,该坐标与方程
x2-x-6=0的解的关系:______________________
(2).当x取__________时,y=0?
当x取__________时,y>0?
当x取__________时,y<0?
(3).由图象写出:
不等式x2 -x-6>0 的解集_________
不等式x2 -x-6<0 的解集_________-23Y<0yxo(-2,0) (3,0)交点的横坐标即为方程的根x= -2 , 3x<-2 或 x>3-23﹜﹛x|-2(1) 2x2-3x-2>0
2解:令2x2-3x-2=0
(2) - x2 + 3x + 10 > 0
∵△=9+16=25>0 方程2x2-3x-2=0的解是x1=-1/2 x2=2
∴原不等式的解集为{x|x<-1/2或x>2} 令 x2-3x - 10 = 0
∵△= 9 + 40 = 49 > 0
方程x2-3x - 10 = 0的解是x1=-2 , x2=5
∴原不等式的解集为{x | -2 < x < 5}解: x2-3x - 10<0 (3) 4x2-4x+1>0 0.5解:令4x2-4x+1=0
∵△=16-16=0
方程4x2-4x+1=0的解是 x1=x2=1/2
∴原不等式的解集为{x|x≠1/2}
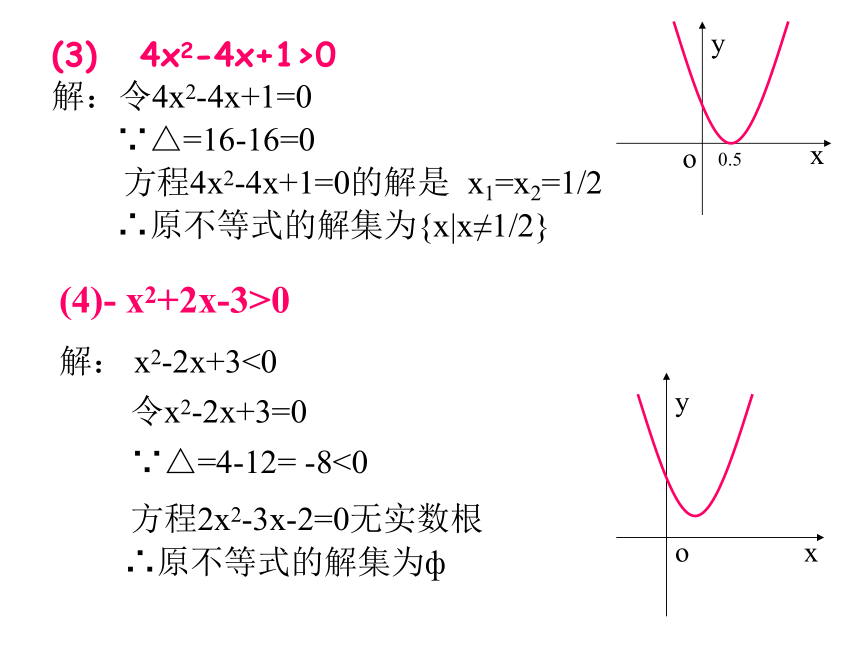
(4)- x2+2x-3>0
解: x2-2x+3<0
令x2-2x+3=0
∵△=4-12= -8<0
方程2x2-3x-2=0无实数根
∴原不等式的解集为фxxyyoo 一般地,一元二次不等式的解集如下表:x1x2xyoxyoxyo两个不相等的实根
x1, x2两个相等
的实根
x= -b/2a﹛x|xx2﹜无实根﹛x|x≠
-b/2a﹜R﹛x|x10(a>0)
ax2+bx+c<0 (a>0)
(2)求△ ,并求出方程ax2+bx+c=0 的实根
(3)根据图象写出解集例1 求函数f(x)= x2-6x+8 的定义域。应用一.定义域问题解: ∴ x2-6x+8≥0的解为x≥4或x≤2
∴原不等式的解集为{x│x≥4或x≤2 }(变)函数f(x)= kx2 -6kx+(k+8)的定义域为R(K>0) 求K的取值范围 解:∵函数f(x)=kx2 -6kx+(k+8)的定义域为R且k>0∴只要△≤0 即(6k)2-4k(k+8)=32k2-32K≤0
∴ 0≤k≤1 又K>0 ∴ 0(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围。
(2)对于x??1,3?,f(x)<-m+5恒成立,求m的取值范围。例2(1)已知一元二次不等式a x2 +bx+6>0 的解集
为{x │- 2 <x<3},求a-b的值
解:一元二次不等式是通过一次方程的根来确定
则可以理解为方程a x2 +bx+6=0的根-2,3
又∵解在两根之间 ∴a<0
-b/a=-2+3=1∴b=1
则a-b=-26/a=-6∴a=-1 ∴应用二.集合问题(2)已知集合A={x│ x2 -ax ≤x-a} B={x│1≤x≤3},若A∩B=A求实数a取值范围
解:A∩B=A,则A ?B
而A :若a≥1 则1≤x≤a 1≤a≤3
若a<1 则 a≤x≤1 那么A ?B
∴a取值范围是1≤a≤3
练习A={x│-1≤x≤1}B={x│x2+(a+1)x+a≤0}
若A∩B=B求a的取值范围 应用三 最值问题0xy1-1例3求函数y= x2-2x+1 x∈[ - 1,1]
上的最值解:∵函数y=x 2-2x+1的对称轴为x=1 又x∈[ - 1,1]
∴ ymax =f(-1)=1+2+1=4 ∴ ymin=f(1)=0练习(1)求函数y=ax 2 -2x+1(a>0) x∈
[ - 1,1]的最值 (2)求函数y=x2+ax-3 , x∈[0,2]的最值
xyo引例1. 如何作出一次函数y=2x-7的图象? 令x=0 则y= - 7, 得到点A(0,-7)
令y=0则x=3.5,得到点B(3.5,0)
经过两点A、B作直线m即得y=2x-7的图象,如下图:
o-73.5
(1).根据图象得:
X取___________时,y=0即2x-7=0
X取___________时,y>0即2x-7>0
X取___________时,y<0即2x-7<0xyX=3.5X<3.5X>3.5(2).根据图象得:
不等式2x-7>0的解集_____________
不等式2x-7<0的解集_____________ ﹛x|x<7/2﹜﹛x|x>7/2﹜m 引例2.根据一元二次函数y=x2-x-6的图象回答:
(1).图象与x轴交点的坐标为___________,该坐标与方程
x2-x-6=0的解的关系:______________________
(2).当x取__________时,y=0?
当x取__________时,y>0?
当x取__________时,y<0?
(3).由图象写出:
不等式x2 -x-6>0 的解集_________
不等式x2 -x-6<0 的解集_________-23Y<0yxo(-2,0) (3,0)交点的横坐标即为方程的根x= -2 , 3x<-2 或 x>3-2
2解:令2x2-3x-2=0
(2) - x2 + 3x + 10 > 0
∵△=9+16=25>0 方程2x2-3x-2=0的解是x1=-1/2 x2=2
∴原不等式的解集为{x|x<-1/2或x>2} 令 x2-3x - 10 = 0
∵△= 9 + 40 = 49 > 0
方程x2-3x - 10 = 0的解是x1=-2 , x2=5
∴原不等式的解集为{x | -2 < x < 5}解: x2-3x - 10<0 (3) 4x2-4x+1>0 0.5解:令4x2-4x+1=0
∵△=16-16=0
方程4x2-4x+1=0的解是 x1=x2=1/2
∴原不等式的解集为{x|x≠1/2}
(4)- x2+2x-3>0
解: x2-2x+3<0
令x2-2x+3=0
∵△=4-12= -8<0
方程2x2-3x-2=0无实数根
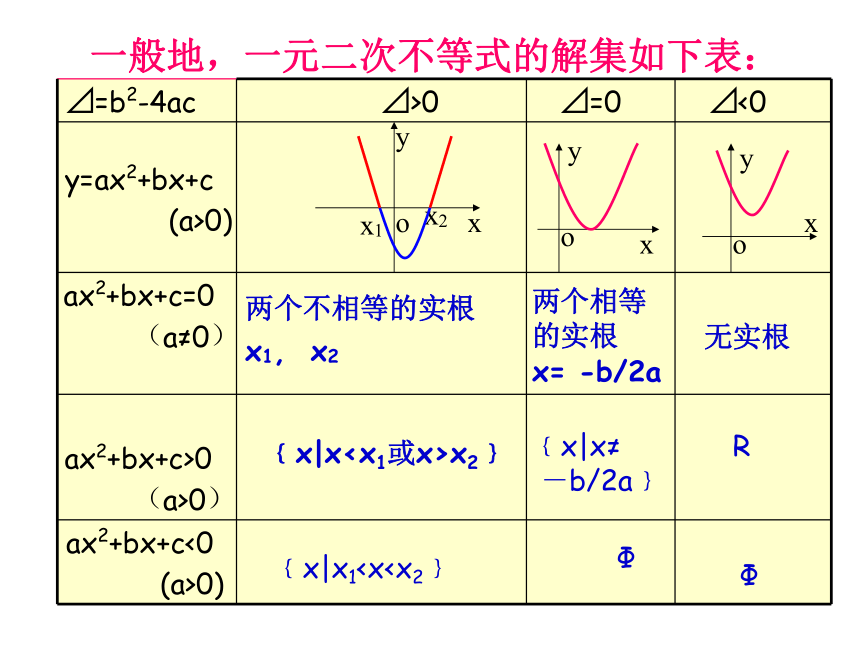
∴原不等式的解集为фxxyyoo 一般地,一元二次不等式的解集如下表:x1x2xyoxyoxyo两个不相等的实根
x1, x2两个相等
的实根
x= -b/2a﹛x|x
-b/2a﹜R﹛x|x1
ax2+bx+c<0 (a>0)
(2)求△ ,并求出方程ax2+bx+c=0 的实根
(3)根据图象写出解集例1 求函数f(x)= x2-6x+8 的定义域。应用一.定义域问题解: ∴ x2-6x+8≥0的解为x≥4或x≤2
∴原不等式的解集为{x│x≥4或x≤2 }(变)函数f(x)= kx2 -6kx+(k+8)的定义域为R(K>0) 求K的取值范围 解:∵函数f(x)=kx2 -6kx+(k+8)的定义域为R且k>0∴只要△≤0 即(6k)2-4k(k+8)=32k2-32K≤0
∴ 0≤k≤1 又K>0 ∴ 0
(2)对于x??1,3?,f(x)<-m+5恒成立,求m的取值范围。例2(1)已知一元二次不等式a x2 +bx+6>0 的解集
为{x │- 2 <x<3},求a-b的值
解:一元二次不等式是通过一次方程的根来确定
则可以理解为方程a x2 +bx+6=0的根-2,3
又∵解在两根之间 ∴a<0
-b/a=-2+3=1∴b=1
则a-b=-26/a=-6∴a=-1 ∴应用二.集合问题(2)已知集合A={x│ x2 -ax ≤x-a} B={x│1≤x≤3},若A∩B=A求实数a取值范围
解:A∩B=A,则A ?B
而A :若a≥1 则1≤x≤a 1≤a≤3
若a<1 则 a≤x≤1 那么A ?B
∴a取值范围是1≤a≤3
练习A={x│-1≤x≤1}B={x│x2+(a+1)x+a≤0}
若A∩B=B求a的取值范围 应用三 最值问题0xy1-1例3求函数y= x2-2x+1 x∈[ - 1,1]
上的最值解:∵函数y=x 2-2x+1的对称轴为x=1 又x∈[ - 1,1]
∴ ymax =f(-1)=1+2+1=4 ∴ ymin=f(1)=0练习(1)求函数y=ax 2 -2x+1(a>0) x∈
[ - 1,1]的最值 (2)求函数y=x2+ax-3 , x∈[0,2]的最值
