一元二次不等式的解法[上学期]
文档属性
| 名称 | 一元二次不等式的解法[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 694.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-08 08:16:00 | ||
图片预览




文档简介
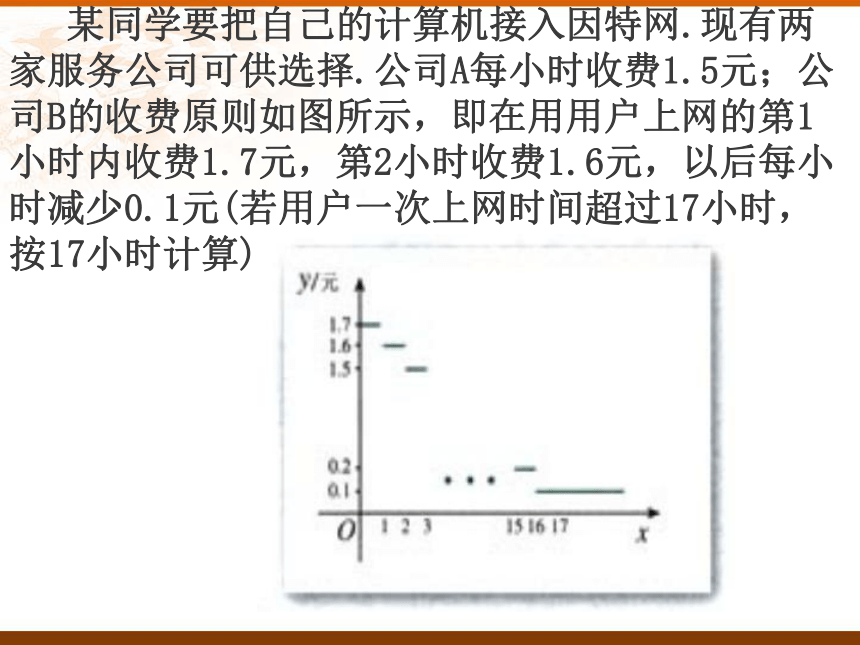
课件17张PPT。不等式的性质反向性—a>b传递性—a>b,b>c可加性—a>b移项法则—a+c>b同向可加—a>b,c>d可乘性—a>b,同向正可乘—a>b>0,c>d>0可乘方—a>b>0可开方—a>b>0(n?R+)(n?N)例 题一元二次不等式的解法 某同学要把自己的计算机接入因特网.现有两家服务公司可供选择.公司A每小时收费1.5元;公司B的收费原则如图所示,即在用用户上网的第1小时内收费1.7元,第2小时收费1.6元,以后每小时减少0.1元(若用户一次上网时间超过17小时,按17小时计算).假设一次上网x小时,则公司A收取的费用为
1.5x(元), 公司B收取的费用为 如果能够保证选择公司A比选择公司B收取的费用
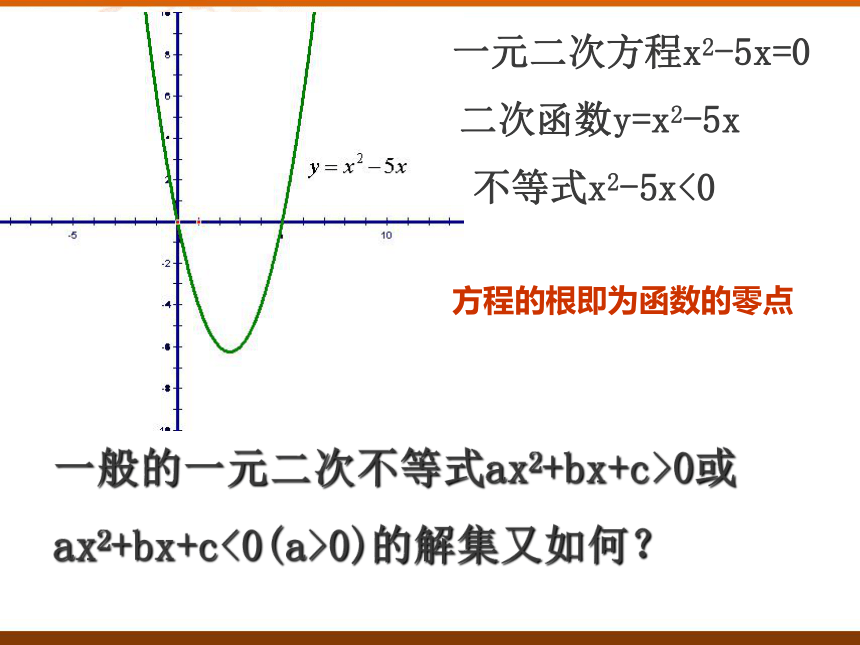
少,则整理得 x2-5x<0.不等式x2-5x<0二次函数y=x2-5x一元二次方程x2-5x=0一般的一元二次不等式ax2+bx+c>0或
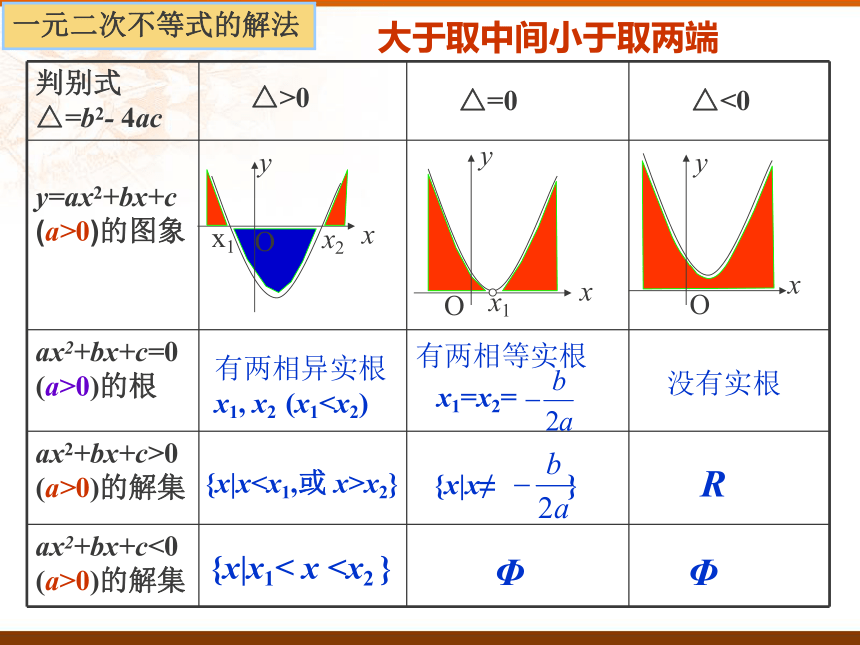
ax2+bx+c<0(a>0)的解集又如何?方程的根即为函数的零点△>0有两相异实根
x1, x2 (x1x2}{x|x1< x x1=x2={x|x≠ }ΦΦR没有实根一元二次不等式的解法大于取中间小于取两端 求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图:x< x1或x> x2例题分析解:根据题意,有整理,得例题分析练习1 -12 -2 解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0) 的步骤是: (1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0) 二次项系数化成正数
(2)判定△与0的关系,并求出方程ax2+bx+c=0
的实根;
(3)最后根据对应的二次函数的大致图象以及
不等号的方向,写出不等式的解集. (大于取中间小于取两端).小结P90习题3.2 A组 第1、2 、3、4题
A本3.2(一)作业小结一、一元二次方程、一元二次不等式和二次函数的关系(1)方程的解对应于函数图象与x轴的交点;(2) 不等式的解集对应于函数图象与x轴上方(或下方)
部分在x轴上的点.二、解一元二次不等式的基本步骤(2)再解对应的一元二次方程;(3)最后根据对应的二次函数的大致图象以及
不等号的方向,写出不等式的解集.(1)先把二次项系数化成正数;一元二次不等式的解法(a>0)有两个相异的
实根x1,x2
x1 x1=x2没有实根{x|x>x2或x
1.5x(元), 公司B收取的费用为 如果能够保证选择公司A比选择公司B收取的费用
少,则整理得 x2-5x<0.不等式x2-5x<0二次函数y=x2-5x一元二次方程x2-5x=0一般的一元二次不等式ax2+bx+c>0或
ax2+bx+c<0(a>0)的解集又如何?方程的根即为函数的零点△>0有两相异实根
x1, x2 (x1
(a>0)的程序框图:x< x1或x> x2例题分析解:根据题意,有整理,得例题分析练习1 -12 -2 解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0) 的步骤是: (1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0) 二次项系数化成正数
(2)判定△与0的关系,并求出方程ax2+bx+c=0
的实根;
(3)最后根据对应的二次函数的大致图象以及
不等号的方向,写出不等式的解集. (大于取中间小于取两端).小结P90习题3.2 A组 第1、2 、3、4题
A本3.2(一)作业小结一、一元二次方程、一元二次不等式和二次函数的关系(1)方程的解对应于函数图象与x轴的交点;(2) 不等式的解集对应于函数图象与x轴上方(或下方)
部分在x轴上的点.二、解一元二次不等式的基本步骤(2)再解对应的一元二次方程;(3)最后根据对应的二次函数的大致图象以及
不等号的方向,写出不等式的解集.(1)先把二次项系数化成正数;一元二次不等式的解法(a>0)有两个相异的
实根x1,x2
x1
