用基本不等式求最值[下学期]
图片预览







文档简介
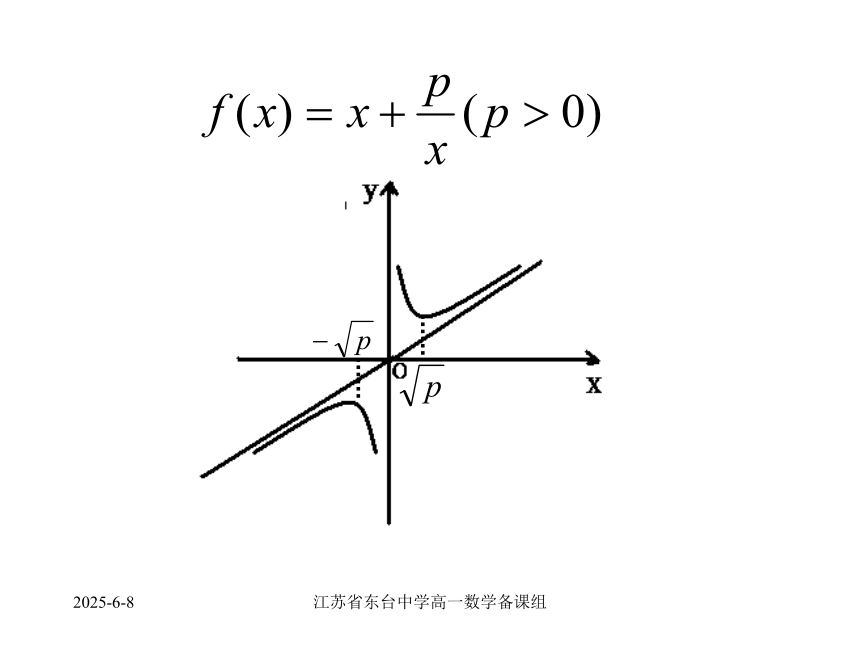
课件22张PPT。2019/3/16江苏省东台中学高一数学备课组不等式的应用———利用基本不等式
求最值
2019/3/16江苏省东台中学高一数学备课组[基础知识]
(1)定理1:如果a,b∈R,那么a2+b2______2ab(当且仅当_______时取等号)
(2)定理2:如果a,b∈R+,那么 (当且仅当_______时取等号)
(3)?均值定理:已知x,y∈R+,x+y=S,xy=P.
??? 如果P是定值,那么当且仅当_______时,S的值有最_____值。
如果S是定值,那么当且仅当_______时,P的值有最_____值。
≥a=b≥a=b
x=yx=y小大2019/3/16江苏省东台中学高一数学备课组(2000年)若(A)R?P ? Q (B)P ? Q ? R
(C)Q ? P ? R (D)P ? R ? Q2019/3/16江苏省东台中学高一数学备课组1)下列函数中,最小值为4的是( )
(A)
(B)
(C)
(D)
≥ = 4∴y的最小值为4
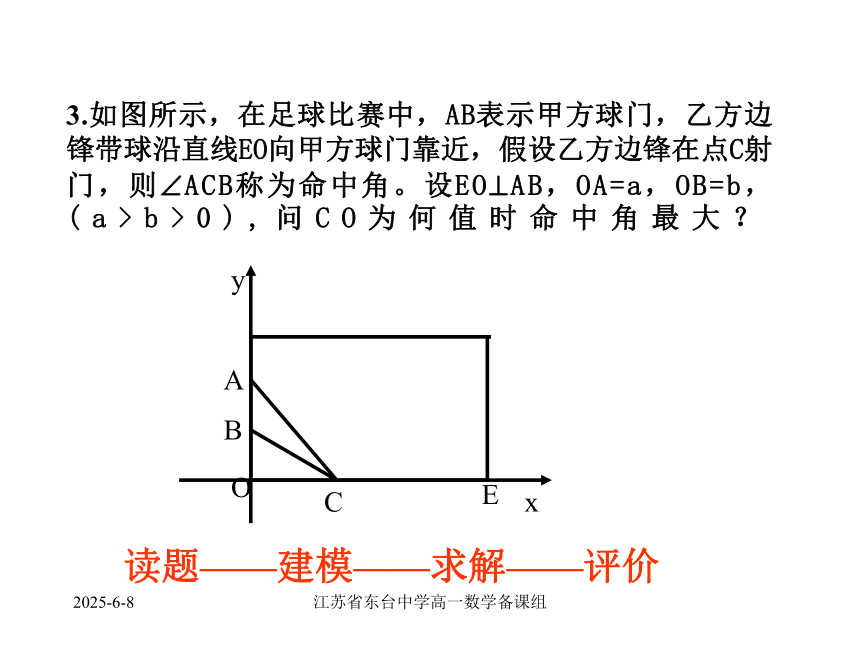
等号在x=1时取得,代入得y≥42019/3/16江苏省东台中学高一数学备课组2019/3/16江苏省东台中学高一数学备课组(2001年)设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ( λ〈1),画面的上、下各留8cm空白,左右各留5cm空白,怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小2019/3/16江苏省东台中学高一数学备课组3.如图所示,在足球比赛中,AB表示甲方球门,乙方边锋带球沿直线EO向甲方球门靠近,假设乙方边锋在点C射门,则?ACB称为命中角。设EO?AB,OA=a,OB=b,(a>b>0),问CO为何值时命中角最大? ABOCExy读题——建模——求解——评价
2019/3/16江苏省东台中学高一数学备课组变式题:已知x,y为正数,且x+2y=1求lgx+lgy的最大值。2019/3/16江苏省东台中学高一数学备课组5)(99理(17)年)若正数a,b满足ab=a+b+3,则ab的取值范围是_____________(98理(22)题)若正数a,b满足2b+ab+a=30,求ab的最大值.
2019/3/16江苏省东台中学高一数学备课组小结:质疑:作业:2019/3/16江苏省东台中学高一数学备课组1)利用基本不等式求最值的条件为“一正,二定,三相等”
小结:2)解决实际问题注意:
审题——建模——求解——评价
3)注重分类讨论、换元、化归等数学思想方法在解题中的运用
2019/3/16江苏省东台中学高一数学备课组2019/3/16江苏省东台中学高一数学备课组
不等式的应用体现在整个中学数学中,如集合问题,方程(组)的解的讨论,函数的定义域,值域,单调性,以及三角,解几,数列,复数,立几中的最值等
2019/3/16江苏省东台中学高一数学备课组变式题:若正数a,b满足ab≥a+b+3,则a+b的最小值是_____________2)已知函数 的值域
是[9,+∞),求实数n的值
2019/3/16江苏省东台中学高一数学备课组(99年)若正数a,b满足ab=a+b+3,则ab的取值范围是_____________2019/3/16江苏省东台中学高一数学备课组(2001年)设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ( λ〈1),画面的上、下各留8cm空白,左右各留5cm空白,怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小2019/3/16江苏省东台中学高一数学备课组如改为求函数2019/3/16江苏省东台中学高一数学备课组变式练习:
(1)已知x>0,y>0,且 求x+y的最小值。
(2)
___________2019/3/16江苏省东台中学高一数学备课组1)下列函数中,最小值为4的是( )
(A)
(B)
(C)
(D)
等号在x=1时取得,代入得y≥42019/3/16江苏省东台中学高一数学备课组(97理(22)题) 甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过C千米/小时,已知汽车每小时的运输成本v(以元为单位)由可变部分和固定部分组成:可变部分与速度(千米/小时)的平方 成正比,比例系数为b;固定部分为a元。 (1)把全程运输成本y(元)表示为速度v(千米/小时)的函数,并指出这个函数的定义域; (2)为了使全程运输成本最小,汽车应以多大的速度行驶?2019/3/16江苏省东台中学高一数学备课组((6)甲、乙两地相距200千米,汽车从甲地匀速行驶到乙地,速度不得超过100千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度(千米/小时)的平方成正比,比例系数为1/100;固定部分为a元。 (1)把全程运输成本y(元)表示为速度v(千米/小时)的函数,并指出这个函数的定义域; (2)为了使全程运输成本最小,汽车应以多大的速度行驶?审题——建模——求解
——评价2019/3/16江苏省东台中学高一数学备课组
求最值
2019/3/16江苏省东台中学高一数学备课组[基础知识]
(1)定理1:如果a,b∈R,那么a2+b2______2ab(当且仅当_______时取等号)
(2)定理2:如果a,b∈R+,那么 (当且仅当_______时取等号)
(3)?均值定理:已知x,y∈R+,x+y=S,xy=P.
??? 如果P是定值,那么当且仅当_______时,S的值有最_____值。
如果S是定值,那么当且仅当_______时,P的值有最_____值。
≥a=b≥a=b
x=yx=y小大2019/3/16江苏省东台中学高一数学备课组(2000年)若(A)R?P ? Q (B)P ? Q ? R
(C)Q ? P ? R (D)P ? R ? Q2019/3/16江苏省东台中学高一数学备课组1)下列函数中,最小值为4的是( )
(A)
(B)
(C)
(D)
≥ = 4∴y的最小值为4
等号在x=1时取得,代入得y≥42019/3/16江苏省东台中学高一数学备课组2019/3/16江苏省东台中学高一数学备课组(2001年)设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ( λ〈1),画面的上、下各留8cm空白,左右各留5cm空白,怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小2019/3/16江苏省东台中学高一数学备课组3.如图所示,在足球比赛中,AB表示甲方球门,乙方边锋带球沿直线EO向甲方球门靠近,假设乙方边锋在点C射门,则?ACB称为命中角。设EO?AB,OA=a,OB=b,(a>b>0),问CO为何值时命中角最大? ABOCExy读题——建模——求解——评价
2019/3/16江苏省东台中学高一数学备课组变式题:已知x,y为正数,且x+2y=1求lgx+lgy的最大值。2019/3/16江苏省东台中学高一数学备课组5)(99理(17)年)若正数a,b满足ab=a+b+3,则ab的取值范围是_____________(98理(22)题)若正数a,b满足2b+ab+a=30,求ab的最大值.
2019/3/16江苏省东台中学高一数学备课组小结:质疑:作业:2019/3/16江苏省东台中学高一数学备课组1)利用基本不等式求最值的条件为“一正,二定,三相等”
小结:2)解决实际问题注意:
审题——建模——求解——评价
3)注重分类讨论、换元、化归等数学思想方法在解题中的运用
2019/3/16江苏省东台中学高一数学备课组2019/3/16江苏省东台中学高一数学备课组
不等式的应用体现在整个中学数学中,如集合问题,方程(组)的解的讨论,函数的定义域,值域,单调性,以及三角,解几,数列,复数,立几中的最值等
2019/3/16江苏省东台中学高一数学备课组变式题:若正数a,b满足ab≥a+b+3,则a+b的最小值是_____________2)已知函数 的值域
是[9,+∞),求实数n的值
2019/3/16江苏省东台中学高一数学备课组(99年)若正数a,b满足ab=a+b+3,则ab的取值范围是_____________2019/3/16江苏省东台中学高一数学备课组(2001年)设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ( λ〈1),画面的上、下各留8cm空白,左右各留5cm空白,怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小2019/3/16江苏省东台中学高一数学备课组如改为求函数2019/3/16江苏省东台中学高一数学备课组变式练习:
(1)已知x>0,y>0,且 求x+y的最小值。
(2)
___________2019/3/16江苏省东台中学高一数学备课组1)下列函数中,最小值为4的是( )
(A)
(B)
(C)
(D)
等号在x=1时取得,代入得y≥42019/3/16江苏省东台中学高一数学备课组(97理(22)题) 甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过C千米/小时,已知汽车每小时的运输成本v(以元为单位)由可变部分和固定部分组成:可变部分与速度(千米/小时)的平方 成正比,比例系数为b;固定部分为a元。 (1)把全程运输成本y(元)表示为速度v(千米/小时)的函数,并指出这个函数的定义域; (2)为了使全程运输成本最小,汽车应以多大的速度行驶?2019/3/16江苏省东台中学高一数学备课组((6)甲、乙两地相距200千米,汽车从甲地匀速行驶到乙地,速度不得超过100千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度(千米/小时)的平方成正比,比例系数为1/100;固定部分为a元。 (1)把全程运输成本y(元)表示为速度v(千米/小时)的函数,并指出这个函数的定义域; (2)为了使全程运输成本最小,汽车应以多大的速度行驶?审题——建模——求解
——评价2019/3/16江苏省东台中学高一数学备课组
