数学人教A版(2019)选修第二册第5章一元函数的导数及其应用单元复习 课件(共34张ppt)
文档属性
| 名称 | 数学人教A版(2019)选修第二册第5章一元函数的导数及其应用单元复习 课件(共34张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 08:08:08 | ||
图片预览










文档简介
(共34张PPT)
第 5 章一元函数的导数及其应用
人教A版2019选修第一册
单元复习课件
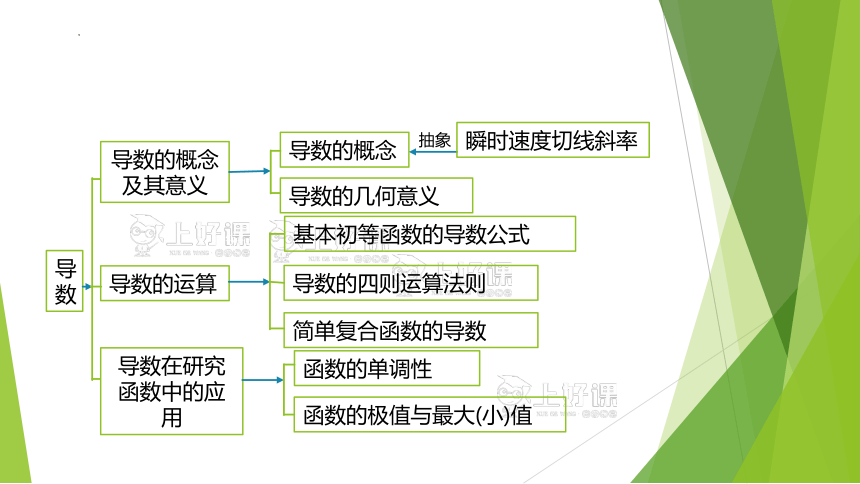
导数的概念及其意义
导数的运算
导数在研究函数中的应用
导数
导数的概念
导数的几何意义
瞬时速度切线斜率
抽象
基本初等函数的导数公式
导数的四则运算法则
简单复合函数的导数
函数的单调性
函数的极值与最大(小)值
典例解析
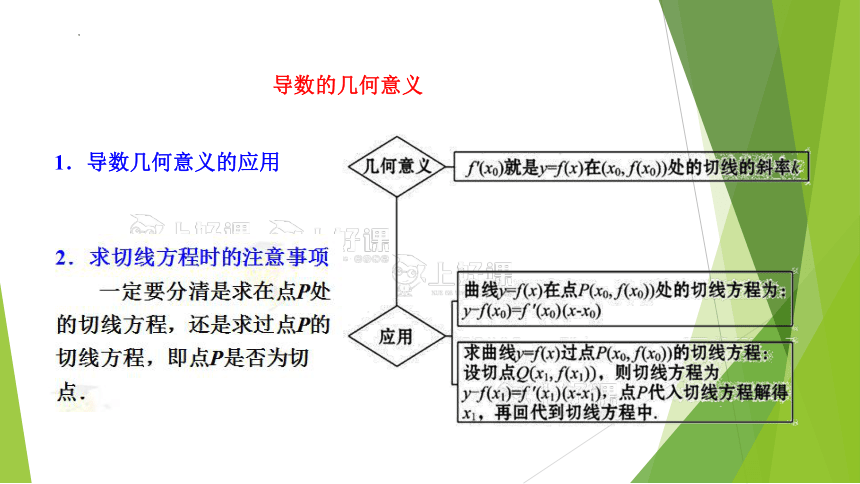
导数的几何意义
1.导数几何意义的应用
归纳总结
典例解析
归纳总结
典例解析
应用导数求函数极值的一般步骤
(1)确定函数f (x)的定义域;
(2)求方程f ′(x)=0的根;
(3)检验f ′(x)=0的根的两侧f ′(x)的符号.
若左正右负,则f (x)在此根处取得极大值;
若左负右正,则f (x)在此根处取得极小值;
否则,此根不是f (x)的极值点.
求函数f (x)在闭区间[a,b]上最值的方法与步骤
(1)求f (x)在(a,b)内的极值;
(2)将(1)求得的极值与f (a),f (b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.
(3)当f (x)在[a,b]上单调时,其最值在区间端点取得;
(4)当f (x)在(a,b)内只有一个极值点时,若在这一点处f (x)有极大(小)值,则可以断定f (x)在该点处取得最大(小)值,这里(a,b)也可以是(-∞,+∞).
归纳总结
典例解析
归纳总结
真题演练
5x-y+2=0
THANKS
“
”
第 5 章一元函数的导数及其应用
人教A版2019选修第一册
单元复习课件
导数的概念及其意义
导数的运算
导数在研究函数中的应用
导数
导数的概念
导数的几何意义
瞬时速度切线斜率
抽象
基本初等函数的导数公式
导数的四则运算法则
简单复合函数的导数
函数的单调性
函数的极值与最大(小)值
典例解析
导数的几何意义
1.导数几何意义的应用
归纳总结
典例解析
归纳总结
典例解析
应用导数求函数极值的一般步骤
(1)确定函数f (x)的定义域;
(2)求方程f ′(x)=0的根;
(3)检验f ′(x)=0的根的两侧f ′(x)的符号.
若左正右负,则f (x)在此根处取得极大值;
若左负右正,则f (x)在此根处取得极小值;
否则,此根不是f (x)的极值点.
求函数f (x)在闭区间[a,b]上最值的方法与步骤
(1)求f (x)在(a,b)内的极值;
(2)将(1)求得的极值与f (a),f (b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.
(3)当f (x)在[a,b]上单调时,其最值在区间端点取得;
(4)当f (x)在(a,b)内只有一个极值点时,若在这一点处f (x)有极大(小)值,则可以断定f (x)在该点处取得最大(小)值,这里(a,b)也可以是(-∞,+∞).
归纳总结
典例解析
归纳总结
真题演练
5x-y+2=0
THANKS
“
”
