不等式证明[下学期]
图片预览





文档简介
课件12张PPT。不等式证明宿迁市马陵中学 李旭一、考点分析 1、重视对基础知识的考查,设问方式不断创新,重点考查四种题型:证明不等式、解不等式、涉及不等式的综合题、涉及不等式的应用题。2、考纲要求:
(1)理解不等式的性质及其证明。
(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用。
(3)掌握分析法、综合法、比较法证明简单的不等式。
(4)掌握简单不等式的解法。
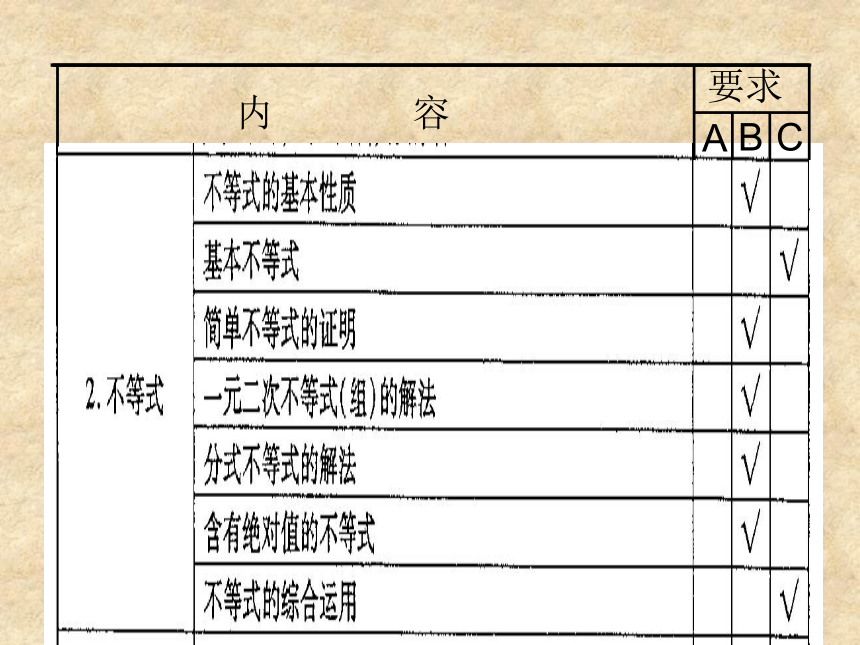
(5)理解不等式|a|-|b|≤|a+b|≤|a|+|b|内 容 要求ACB知识检索1、已知 那么( )2、若 则下列不等式中正确有 。D1、4、6、73、下列结论正确的是( )BCC例1、求使 ≤a (x>0,y>0)恒成立的a的最小值.解法一:由于a的值为正数,将已知不等式两边平方,得:x+y+2 ≤a2(x+y),即2 ≤(a2-1)(x+y), ①
∴x,y>0,∴x+y≥2 , ② 比较①、②得a的最小值满足a2-1=1,
∴a2=2,a= (因a>0),∴a的最小值是当且仅当x=y时,②中有等号成立.解二:设∵x>0,y>0,∴x+y≥2 (当x=y时“=”成立),∴ ≤1, 的最大值是1.从而可知,u的最大值为 ,又由已知,得a≥u,∴a的最小值为 .解法三:∵y>0,
∴原不等式可化为 +1≤a ,设 =tanθ,θ∈(0, ).∴tanθ+1≤a ;即tanθ+1≤asecθ∴a≥sinθ+cosθ= sin(θ+ ), ③又∵sin(θ+ )的最大值为1(此时θ= ).
由③式可知a的最小值为 .1.不等式证明常用的方法有:比较法、综合法和分析法,它们是证明不等式的最基本的方法.
(1)比较法证不等式有作差(商)、变形、判断三个步骤,变形的主要方向是因式分解、配方,判断过程必须详细叙述;如果作差以后的式子可以整理为关于某一个变量的二次式,则考虑用判别式法证.
(2)综合法是由因导果,而分析法是执果索因,两法相互转换,互相渗透,互为前提,充分运用这一辩证关系,可以增加解题思路,开扩视野.2.不等式证明还有一些常用的方法:换元法、放缩法、反证法、函数单调性法、判别式法、数形结合法等.换元法主要有三角代换,均值代换两种,在应用换元法时,要注意代换的等价性.放缩性是不等式证明中最重要的变形方法之一,放缩要有的放矢,目标可以从要证的结论中考查.有些不等式,从正面证如果不易说清楚,可以考虑反证法.凡是含有“至少”“惟一”或含有其他否定词的命题,适宜用反证法.
证明不等式时,要依据题设、题目的特点和内在联系,选择适当的证明方法,要熟悉各种证法中的推理思维,并掌握相应的步骤、技巧和语言特点.解例2
(1)理解不等式的性质及其证明。
(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用。
(3)掌握分析法、综合法、比较法证明简单的不等式。
(4)掌握简单不等式的解法。
(5)理解不等式|a|-|b|≤|a+b|≤|a|+|b|内 容 要求ACB知识检索1、已知 那么( )2、若 则下列不等式中正确有 。D1、4、6、73、下列结论正确的是( )BCC例1、求使 ≤a (x>0,y>0)恒成立的a的最小值.解法一:由于a的值为正数,将已知不等式两边平方,得:x+y+2 ≤a2(x+y),即2 ≤(a2-1)(x+y), ①
∴x,y>0,∴x+y≥2 , ② 比较①、②得a的最小值满足a2-1=1,
∴a2=2,a= (因a>0),∴a的最小值是当且仅当x=y时,②中有等号成立.解二:设∵x>0,y>0,∴x+y≥2 (当x=y时“=”成立),∴ ≤1, 的最大值是1.从而可知,u的最大值为 ,又由已知,得a≥u,∴a的最小值为 .解法三:∵y>0,
∴原不等式可化为 +1≤a ,设 =tanθ,θ∈(0, ).∴tanθ+1≤a ;即tanθ+1≤asecθ∴a≥sinθ+cosθ= sin(θ+ ), ③又∵sin(θ+ )的最大值为1(此时θ= ).
由③式可知a的最小值为 .1.不等式证明常用的方法有:比较法、综合法和分析法,它们是证明不等式的最基本的方法.
(1)比较法证不等式有作差(商)、变形、判断三个步骤,变形的主要方向是因式分解、配方,判断过程必须详细叙述;如果作差以后的式子可以整理为关于某一个变量的二次式,则考虑用判别式法证.
(2)综合法是由因导果,而分析法是执果索因,两法相互转换,互相渗透,互为前提,充分运用这一辩证关系,可以增加解题思路,开扩视野.2.不等式证明还有一些常用的方法:换元法、放缩法、反证法、函数单调性法、判别式法、数形结合法等.换元法主要有三角代换,均值代换两种,在应用换元法时,要注意代换的等价性.放缩性是不等式证明中最重要的变形方法之一,放缩要有的放矢,目标可以从要证的结论中考查.有些不等式,从正面证如果不易说清楚,可以考虑反证法.凡是含有“至少”“惟一”或含有其他否定词的命题,适宜用反证法.
证明不等式时,要依据题设、题目的特点和内在联系,选择适当的证明方法,要熟悉各种证法中的推理思维,并掌握相应的步骤、技巧和语言特点.解例2
