不等式证明方法[下学期]
图片预览








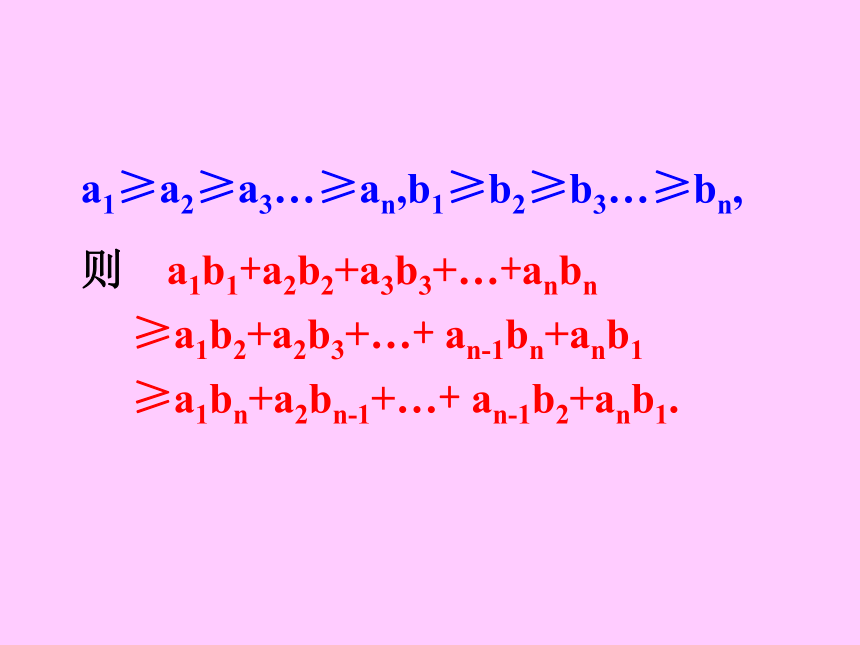
文档简介
课件23张PPT。不 等 式 的 证 明【例1】已知a>0,b>0,求证:a3+b3≥a2b+ab2.(课本P12例3)即a3+b3≥a2b+ab2.证明一:比较法(作差)(a3+b3)-(a2b+ab2)=(a3- a2b)+(b3-ab2)=a2(a-b)+b2(b-a)∵a>0,b>0,∴( a-b)2(a+b)≥0.故(a3+b3)-(a2b+ab2)≥0,∴a+b>0,而( a-b)2≥0.=( a-b)2(a+b).=(a-b)( a2-b2)故a3+b3≥a2b+ab2.证明二:比较法(作商)∵a2+b2≥2ab,∴又a>0,b>0,所以ab>0,所以有a3+b3≥a2b+ab2.证明三:分析法欲证a3+b3≥a2b+ab2,只需证明(a+b)(a2+b2-ab)≥ab(a+b).由于a>0,b>0,所以a+b>0,故只要证明a2+b2-ab≥ab即可。即证明a2+b2≥2ab.而a2+b2≥2ab 显然是成立的即a3+b3≥a2b+ab2.证明四:综合法∵a2+b2≥2ab,∴a2+b2-ab≥ab.又∵a>0,b>0,∴a+b>0,故(a+b)(a2+b2-ab)≥ab(a+b).【例2】已知a>0,b>0,求证:证明一:比较法(作差)证明二:比较法(作商)而a>0,b>0,所以a+b>0. 证明四:综合法a1≥a2≥a3…≥an,b1≥b2≥b3…≥bn, ≥a1bn+a2bn-1+…+ an-1b2+anb1.≥a1b2+a2b3+…+ an-1bn+anb1则 a1b1+a2b2+a3b3+…+anbn【例3】求证:(ac+bd)2≤(a2+b2)(c2+d2).证明一:(比较法)∵(ac+bd)2-(a2+b2)(c2+d2)∴ (ac+bd)2≤(a2+b2)(c2+d2).=2abcd- a2d2-b2c2=(a2c2+b2d2+2abcd)-(a2c2+b2d2+a2d2+b2c2)=-(ad-bc)2≤0.证明二:(分析法)证明三:(综合法)一般地,对任意实数ai,bi(i=1,2,3, …,n),都有:
(a12+a22+…+an2)(b12+b22+…+bn2)
≥(a1b1+a2b2+…+anbn) 2.(柯西不等式)【例4】设-1 .证明一:比较法(作差)∵-10,1-a2>0,1-b2>0,1-ab>0.所以,(1-a2)(1-b2)(1-ab)>0, 证明二:分析法证明三:综合法∵a2+b2≥2ab, ∴-a2-b2≤-2ab.从而0<1+a2b2-a2-b2≤1+a2b2-2ab=(1-ab)2, 1-ab>0.证明四:换元法设a=sinα,b=sinβ,则思考 ≥2+2ab+2a2b2+…=2(1+ab+a2b2+…)【例5】设a>0,b>0,且a+b=1,求证:证明一(分析法)(4a+1)(4b+1) ≤916ab+4a+4b+1≤9 证明二(综合法) 因为a>0,b>0,且a+b=1,所以
从而 +
≤ .【例6】已知m>0,求证:m+ ≥3.证明一(比较法) ∵m+ -3
=∴ m+≥3证明二(综合法)m+ = 证明三(函数思想)设f(x)=x+ ,则f ’(x)=1- ,令f’(x)=0,得: x=2.当02时, f ’(x)>0.所以当x=2时, f(x)取到最大值3, 故当m>0时,有 m+ ≥3. =3 已知二次函数f(x)=ax2+bx+c,方
程f(x)-x=0的两根为x1,x2,且0求证:当x∈(0,x1)时,x
(a12+a22+…+an2)(b12+b22+…+bn2)
≥(a1b1+a2b2+…+anbn) 2.(柯西不等式)【例4】设-1
从而 +
≤ .【例6】已知m>0,求证:m+ ≥3.证明一(比较法) ∵m+ -3
=∴ m+≥3证明二(综合法)m+ = 证明三(函数思想)设f(x)=x+ ,则f ’(x)=1- ,令f’(x)=0,得: x=2.当0
程f(x)-x=0的两根为x1,x2,且0
