苏科版九年级下册6.5 相似三角形的性质课件(共41张PPT)
文档属性
| 名称 | 苏科版九年级下册6.5 相似三角形的性质课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 10:10:51 | ||
图片预览






文档简介
(共41张PPT)
相似三角形的性质
Properties of similar triangles
苏科版九年级下册第6章图形的相似
教学目标
01
在探索相似三角形性质的过程中,进一步加深对相似比概念的理解
02
掌握相似三角形的性质定理,理解“对应高”、“对应中线”、“对应角平分线”中的“对应”的含义
03
能借助相似三角形的性质定理去理解相似多边形的性质
相似三角形的性质
知识精讲
复习引入
01
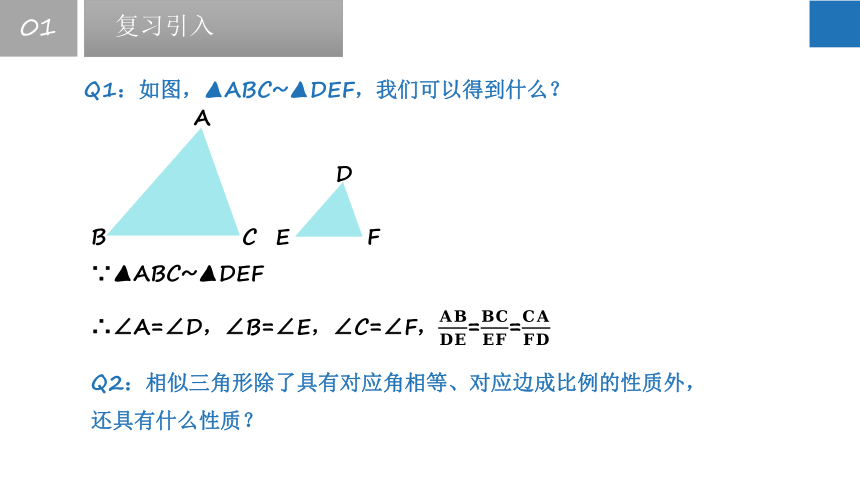
Q1:如图,▲ABC~▲DEF,我们可以得到什么?
C
D
F
A
B
E
Q2:相似三角形除了具有对应角相等、对应边成比例的性质外,还具有什么性质?
∵▲ABC~▲DEF
∴∠A=∠D,∠B=∠E,∠C=∠F,==
知识精讲
情境引入
01
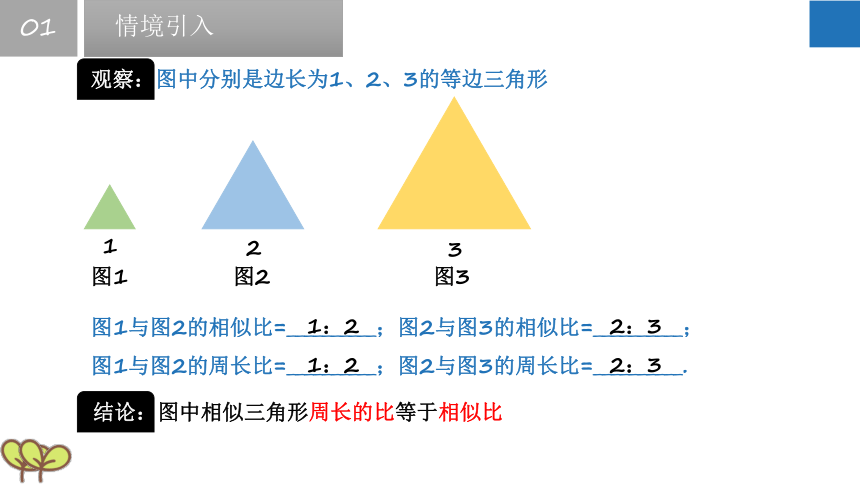
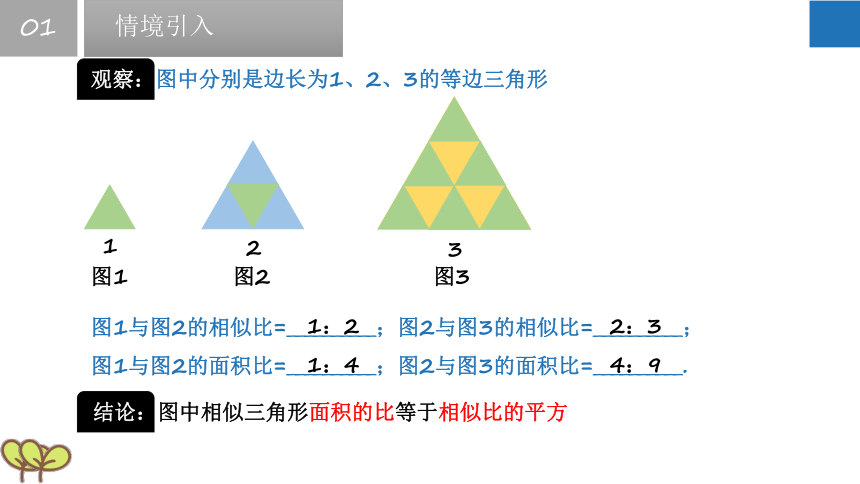
观察:图中分别是边长为1、2、3的等边三角形
3
1
2
图1
图2
图3
图1与图2的相似比=__________;图2与图3的相似比=__________;
图1与图2的周长比=__________;图2与图3的周长比=__________.
1:2
1:2
2:3
2:3
结论:图中相似三角形周长的比等于相似比
知识精讲
情境引入
01
猜想:相似三角形周长的比等于相似比
证明:∵△ABC∽△A'B'C'
∴∠B=∠B’,===k
∴AB=kA'B',BC=kB'C',CA=kC'A'
∴==k,即=k
C
A’
C’
A
B
B’
已知△ABC∽△A’B’C’,相似比为k.
求证:=k.
知识精讲
情境引入
01
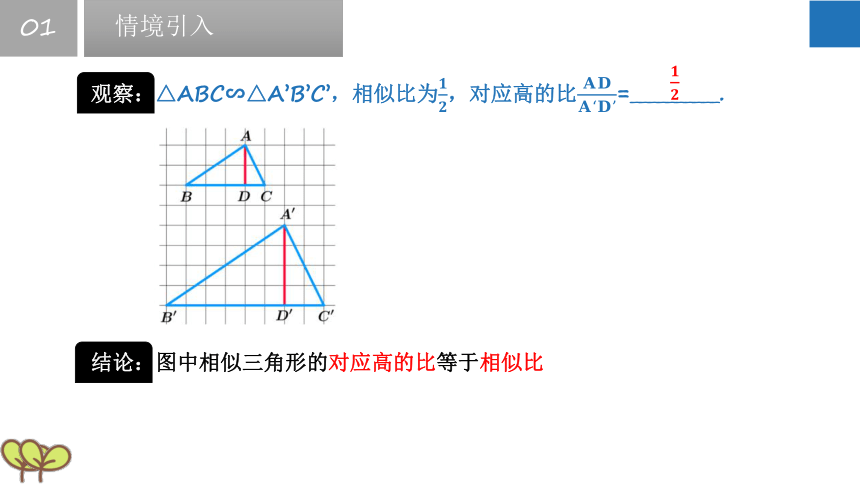
观察:△ABC∽△A’B’C’,相似比为,对应高的比=__________.
结论:图中相似三角形的对应高的比等于相似比
知识精讲
情境引入
01
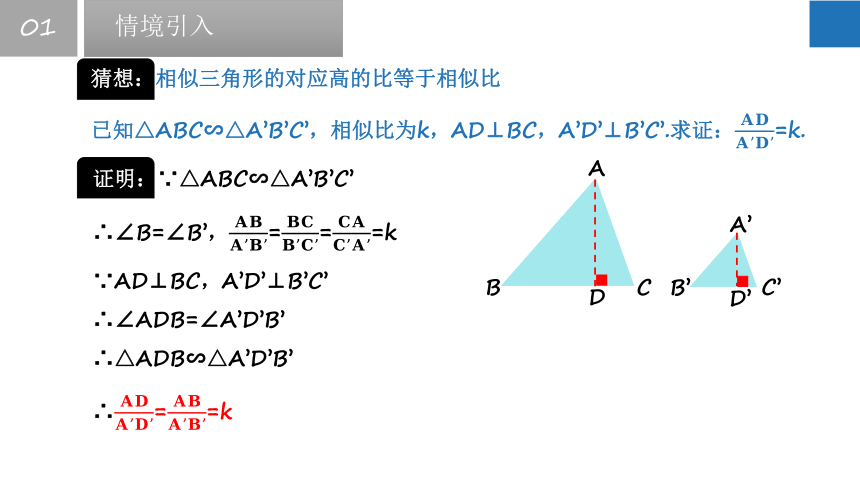
猜想:相似三角形的对应高的比等于相似比
证明:∵△ABC∽△A’B’C’
∴∠B=∠B’,===k
∵AD⊥BC,A’D’⊥B’C’
∴∠ADB=∠A’D’B’
∴△ADB∽△A’D’B’
∴==k
C
A’
C’
A
B
B’
D
D’
已知△ABC∽△A’B’C’,相似比为k,AD⊥BC,A’D’⊥B’C’.求证:=k.
知识精讲
情境引入
01
观察:图中分别是边长为1、2、3的等边三角形
图1与图2的相似比=__________;图2与图3的相似比=__________;
图1与图2的面积比=__________;图2与图3的面积比=__________.
1:2
1:4
2:3
4:9
结论:图中相似三角形面积的比等于相似比的平方
3
1
2
图1
图2
图3
知识精讲
情境引入
01
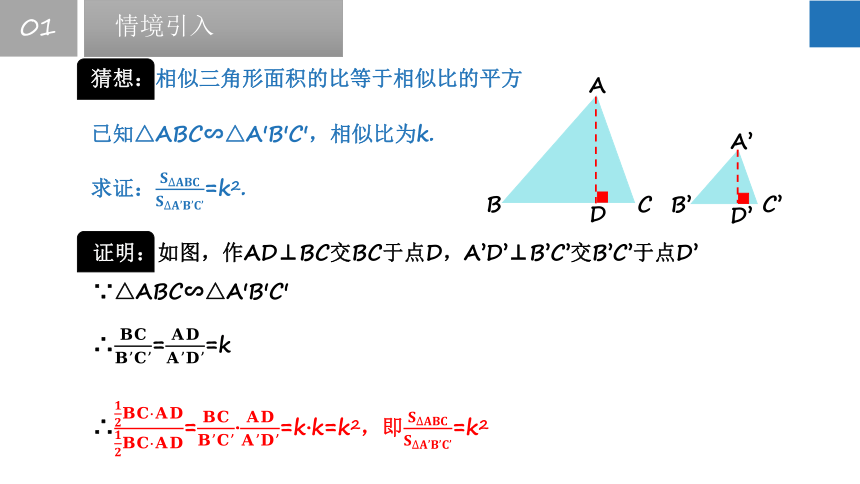
猜想:相似三角形面积的比等于相似比的平方
证明:如图,作AD⊥BC交BC于点D,A’D’⊥B’C’交B’C’于点D’
∵△ABC∽△A'B'C'
∴==k
∴=·=k·k=k2,即=k2
C
A’
C’
A
B
B’
D
D’
已知△ABC∽△A'B'C',相似比为k.
求证:=k2.
02
知识精讲
相似三角形周长的比等于相似比
相似三角形对应高的比等于相似比
相似三角形面积的比等于相似比的平方
相似三角形的性质
知识精讲
情境引入
01
在探索“相似三角形面积的比等于相似比的平方”的过程中,我们发现了“相似三角形对应高的比等于相似比”.
Q3:类似地,相似三角形对应中线、对应角平分线等对应线段的比是否也等于相似比呢?
知识精讲
情境引入
01
观察:△ABC∽△A’B’C’,相似比为,对应中线的比=__________.
结论:图中相似三角形的对应中线的比等于相似比
知识精讲
情境引入
01
猜想:相似三角形的对应中线的比等于相似比
证明:∵△ABC∽△A’B’C’
∴∠B=∠B’,==k
∵D、D’分别为BC、B’C’中点
∴BD=BC,B’D’=B’C’,∴===k=
C
A’
C’
A
B
B’
D
D’
已知△ABC∽△A’B’C’,相似比为k,D、D’分别为BC、B’C’中点.
求证:=k.
∵∠B=∠B’,==k
∴△ABD∽△A’B’D’,∴==k
知识精讲
情境引入
01
观察:△ABC∽△A’B’C’,相似比为,对应角平分线的比=__________.
结论:图中相似三角形的对应角平分线的比等于相似比
知识精讲
情境引入
01
猜想:相似三角形的对应角平分线的比等于相似比
证明:∵△ABC∽△A’B’C’
∴∠BAC=∠B’A’C’,∠B=∠B’,=k
∵AD、A’D’分别为∠BAC、∠B’A’C’中点
∴∠BAD=∠BAC,∠B’A’D’=∠B’A’C’
∴∠BAD=∠B’A’D’
C
A’
C’
A
B
B’
D
D’
已知△ABC∽△A’B’C’,相似比为k,AD、A’D’分别为∠BAC、∠B’A’C’中点.
求证:=k.
∵∠B=∠B’,∠BAD=∠B’A’D’
∴△ABD∽△A’B’D’
∴==k
02
知识精讲
相似三角形对应中线的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形的性质
推广:相似三角形对应线段的比等于相似比
02
知识精讲
相似三角形的性质总结
相似三角形 面积的比 等于相似比的平方
周长的比 等于相似比
对应高的比 对应线段的比 对应中线的比 对应角平分线的比 知识精讲
例1、已知△ABC与△A'B'C'相似,相似比为2:3;△A'B'C'与△A''B''C''相似,相似比为5:4,那么△ABC与△A''B''C''的相似比为( )
A.5:6 B.6:5 C.15:8 D.8:15
【分析】
∵△ABC与△A′B′C′的相似比为2:3=10:15,
△A′B′C′与△A″B″C″的相似比为5:4=15:12,
∴△ABC与△A″B″C″相似比为10:12=5:6.
【相似三角形的对应边的性质】
A
知识精讲
例2、如图,已知△ADE∽△ACB,若AB=10,AC=8,AD=4,则AE的长是( )
A.4
B.5
C.20
D.3.2
B
【分析】
∵△ADE∽△ACB,
∴=,
∵AB=10,AC=8,AD=4,
∴=,
解得:AE=5.
知识精讲
例3、如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=,AD=1,求DB的长.
【分析】
∵∠ACD=∠ABC,∠A=∠A,
∴△ACD∽△ABC,∴=,
∵AC=,AD=1,
∴=,∴AB=3,
∴DB=AB-AD=3-1=2.
知识精讲
例4、两个相似三角形的最短边分别为5cm和3cm,它们的周长之和为48cm,那么小三角形的周长为( )
A.12cm B.18cm C.24cm D.30cm
【分析】
根据题意,两三角形的周长的比为5:3,
设两三角形的周长分别为5xcm,3xcm,
则5x+3x=48,解得:x=6,
∴3x=18,即小三角形的周长为18cm.
【相似三角形的周长与面积的性质】
B
知识精讲
例5、两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为( )
A.14cm B.16cm C.18cm D.30cm
【分析】
根据题意,两三角形的周长的比为5:3,
设两三角形的周长分别为5xcm,3xcm,
则5x-3x=12,解得:x=6,
∴3x=18,即小三角形的周长为18cm.
C
知识精讲
例6、如图,△ABC∽△A'B'C',AD和A'D'分别是△ABC和△A′B′C′的高,若AD=2,A'D'=3,则△ABC与△A'B'C'的面积的比为( )
A.4:9 B.9:4 C.2:3 D.3:2
C
【分析】
∵△ABC∽△A'B'C',
AD和A'D'分别是△ABC和△A′B′C′的高,AD=2,A'D'=3,
∴==,
∴△ABC与△A'B'C'的面积的比=()2=.
知识精讲
例7、如图,△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2,则下列等式一定成立的是( )
A.=
B.=
C.=
D.=
D
【分析】
∵△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,
∴=,A错误;=,C错误;=,D正确;
不能得出=,B错误.
知识精讲
例8、下列四个命题中,错误的是( )
A.相似三角形对应角平分线的比等于相似比
B.相似三角形面积的比等于对应中线的比的平方
C.相似三角形对应高的比等于对应中线的比
D.相似三角形周长的比等于相似三角形面积的比
【分析】
A、相似三角形对应角平分线的比等于相似比,A√;
B、相似三角形面积的比等于对应中线的比的平方,B√;
C、相似三角形对应高的比等于对应中线的比,C√;
D、相似三角形周长的比等于相似三角形面积的比的算术平方根,D×.
【相似三角形的对应线段的性质】
D
知识精讲
例9、若△ABC∽△DEF,且△ABC与△DEF的面积比是,则△ABC与△DEF对应角平分线之比为________.
【分析】
∵△ABC∽△DEF,△ABC与△DEF的面积比为,
∴△ABC与△DEF的相似比为=,
∴△ABC与△DEF对应角的角平分线之比为.
相似多边形的性质
知识精讲
复习引入
01
Q1:如图,五边形ABCDE~五边形A’B’C’D’E’,我们可以得到什么?
Q2:同样地,相似多边形除了具有对应角相等、对应边成比例的性质外,还具有什么性质?
∵五边形ABCDE~五边形A’B’C’D’E’
∴∠A=∠A’,∠B=∠B’,∠C=∠C’,∠D=∠D’,∠E=∠E’,====
A
B
C
D
E
A’
B’
C’
D’
E’
知识精讲
情境引入
01
问题:如图,如果两个多边形相似,它们的周长有什么关系?
A
B
C
D
E
A’
B’
C’
D’
E’
猜想:类比相似三角形,相似多边形周长的比等于相似比
知识精讲
情境引入
01
证明:∵五边形ABCDE∽五边形A’B’C’D’E’
∴=====k(设相似比为k)
∴AB=kA'B',BC=kB'C',CD=kC'D',DE=kD'E',EA=kE'A'
∴==k
即=k
A
B
C
D
E
A’
B’
C’
D’
E’
知识精讲
情境引入
01
问题:如图,如果两个多边形相似,它们的面积有什么关系?
A
B
C
D
E
A’
B’
C’
D’
E’
猜想:类比相似三角形,相似多边形面积的比等于相似比的平方
知识精讲
情境引入
01
证明思路:
(一)将两幅图中的五边形分别切割成如图的三个三角形
(二)分别证明两幅图中对应的三组三角形相似
(三)将两幅图中五边形的面积转化成对应图中的三个三角形面积之和
由此可得:=相似比2
A
B
C
D
E
A’
B’
C’
D’
E’
02
知识精讲
相似多边形周长的比等于相似比
相似多边形面积的比等于相似比的平方
相似多边形的性质
知识精讲
例10、如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是________.
【相似多边形的对应边的性质】
【分析】
∵四边形ABCD∽四边形A1B1C1D1,
∴=,
∵AB=12,CD=15,A1B1=9,
∴=,解得:C1D1=.
知识精讲
例11、如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )
A.2
B.2.4
C.2.5
D.3
A
【分析】
∵矩形ABCD∽矩形ADFE,
∴=,
∵AE=1,AB=4,
∴=,解得:AD=2.
知识精讲
例12、下列说法错误的是( )
A.若把一个多边形的各边扩大为原来的k倍,则其周长也扩大为原来的k倍
B.若把一个多边形的面积扩大为原来的k倍,则其各边扩大为原来的k2倍
C.相似三角形的对应中线、对应角平分线、对应高的比都等于相似比
D.相似三角形的面积比等于周长比的平方
【相似多边形的周长与面积的性质】
B
【分析】
A.一个多边形的各边扩大为原来的k倍,其周长也扩大为原来的k倍,A√;
B.一个多边形的面积扩大为原来的k倍,其各边扩大为原来的倍,B×;
C.相似三角形的对应中线、对应角平分线、对应高的比都等于相似比,C√;
D.相似三角形的面积比等于周长比的平方,D√.
知识精讲
例13、若两个相似多边形的面积比为9:64,则它们的周长比为( )
A.8:3 B.3:8 C.9:64 D.64:9
B
知识精讲
例14、若两个相似多边形的面积之比为1:4,周长之差为6,则这两个相似多边形的周长分别是__________.
【分析】
∵两个相似多边形的面积之比为1:4,
∴两个相似多边形的周长之比为1:2,
设两个多边形的周长分别为x,x+6,
则x+6=2x,解得:x=6,
∴这两个相似多边形的周长分别是6,12.
6, 12
课后总结
相似三角形 面积的比 等于相似比的平方
周长的比 等于相似比
对应高的比 对应线段的比 对应中线的比 对应角平分线的比
相似多边形周长的比等于相似比
相似多边形面积的比等于相似比的平方
谢谢学习
Thank you for learning
相似三角形的性质
Properties of similar triangles
苏科版九年级下册第6章图形的相似
教学目标
01
在探索相似三角形性质的过程中,进一步加深对相似比概念的理解
02
掌握相似三角形的性质定理,理解“对应高”、“对应中线”、“对应角平分线”中的“对应”的含义
03
能借助相似三角形的性质定理去理解相似多边形的性质
相似三角形的性质
知识精讲
复习引入
01
Q1:如图,▲ABC~▲DEF,我们可以得到什么?
C
D
F
A
B
E
Q2:相似三角形除了具有对应角相等、对应边成比例的性质外,还具有什么性质?
∵▲ABC~▲DEF
∴∠A=∠D,∠B=∠E,∠C=∠F,==
知识精讲
情境引入
01
观察:图中分别是边长为1、2、3的等边三角形
3
1
2
图1
图2
图3
图1与图2的相似比=__________;图2与图3的相似比=__________;
图1与图2的周长比=__________;图2与图3的周长比=__________.
1:2
1:2
2:3
2:3
结论:图中相似三角形周长的比等于相似比
知识精讲
情境引入
01
猜想:相似三角形周长的比等于相似比
证明:∵△ABC∽△A'B'C'
∴∠B=∠B’,===k
∴AB=kA'B',BC=kB'C',CA=kC'A'
∴==k,即=k
C
A’
C’
A
B
B’
已知△ABC∽△A’B’C’,相似比为k.
求证:=k.
知识精讲
情境引入
01
观察:△ABC∽△A’B’C’,相似比为,对应高的比=__________.
结论:图中相似三角形的对应高的比等于相似比
知识精讲
情境引入
01
猜想:相似三角形的对应高的比等于相似比
证明:∵△ABC∽△A’B’C’
∴∠B=∠B’,===k
∵AD⊥BC,A’D’⊥B’C’
∴∠ADB=∠A’D’B’
∴△ADB∽△A’D’B’
∴==k
C
A’
C’
A
B
B’
D
D’
已知△ABC∽△A’B’C’,相似比为k,AD⊥BC,A’D’⊥B’C’.求证:=k.
知识精讲
情境引入
01
观察:图中分别是边长为1、2、3的等边三角形
图1与图2的相似比=__________;图2与图3的相似比=__________;
图1与图2的面积比=__________;图2与图3的面积比=__________.
1:2
1:4
2:3
4:9
结论:图中相似三角形面积的比等于相似比的平方
3
1
2
图1
图2
图3
知识精讲
情境引入
01
猜想:相似三角形面积的比等于相似比的平方
证明:如图,作AD⊥BC交BC于点D,A’D’⊥B’C’交B’C’于点D’
∵△ABC∽△A'B'C'
∴==k
∴=·=k·k=k2,即=k2
C
A’
C’
A
B
B’
D
D’
已知△ABC∽△A'B'C',相似比为k.
求证:=k2.
02
知识精讲
相似三角形周长的比等于相似比
相似三角形对应高的比等于相似比
相似三角形面积的比等于相似比的平方
相似三角形的性质
知识精讲
情境引入
01
在探索“相似三角形面积的比等于相似比的平方”的过程中,我们发现了“相似三角形对应高的比等于相似比”.
Q3:类似地,相似三角形对应中线、对应角平分线等对应线段的比是否也等于相似比呢?
知识精讲
情境引入
01
观察:△ABC∽△A’B’C’,相似比为,对应中线的比=__________.
结论:图中相似三角形的对应中线的比等于相似比
知识精讲
情境引入
01
猜想:相似三角形的对应中线的比等于相似比
证明:∵△ABC∽△A’B’C’
∴∠B=∠B’,==k
∵D、D’分别为BC、B’C’中点
∴BD=BC,B’D’=B’C’,∴===k=
C
A’
C’
A
B
B’
D
D’
已知△ABC∽△A’B’C’,相似比为k,D、D’分别为BC、B’C’中点.
求证:=k.
∵∠B=∠B’,==k
∴△ABD∽△A’B’D’,∴==k
知识精讲
情境引入
01
观察:△ABC∽△A’B’C’,相似比为,对应角平分线的比=__________.
结论:图中相似三角形的对应角平分线的比等于相似比
知识精讲
情境引入
01
猜想:相似三角形的对应角平分线的比等于相似比
证明:∵△ABC∽△A’B’C’
∴∠BAC=∠B’A’C’,∠B=∠B’,=k
∵AD、A’D’分别为∠BAC、∠B’A’C’中点
∴∠BAD=∠BAC,∠B’A’D’=∠B’A’C’
∴∠BAD=∠B’A’D’
C
A’
C’
A
B
B’
D
D’
已知△ABC∽△A’B’C’,相似比为k,AD、A’D’分别为∠BAC、∠B’A’C’中点.
求证:=k.
∵∠B=∠B’,∠BAD=∠B’A’D’
∴△ABD∽△A’B’D’
∴==k
02
知识精讲
相似三角形对应中线的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形的性质
推广:相似三角形对应线段的比等于相似比
02
知识精讲
相似三角形的性质总结
相似三角形 面积的比 等于相似比的平方
周长的比 等于相似比
对应高的比 对应线段的比 对应中线的比 对应角平分线的比 知识精讲
例1、已知△ABC与△A'B'C'相似,相似比为2:3;△A'B'C'与△A''B''C''相似,相似比为5:4,那么△ABC与△A''B''C''的相似比为( )
A.5:6 B.6:5 C.15:8 D.8:15
【分析】
∵△ABC与△A′B′C′的相似比为2:3=10:15,
△A′B′C′与△A″B″C″的相似比为5:4=15:12,
∴△ABC与△A″B″C″相似比为10:12=5:6.
【相似三角形的对应边的性质】
A
知识精讲
例2、如图,已知△ADE∽△ACB,若AB=10,AC=8,AD=4,则AE的长是( )
A.4
B.5
C.20
D.3.2
B
【分析】
∵△ADE∽△ACB,
∴=,
∵AB=10,AC=8,AD=4,
∴=,
解得:AE=5.
知识精讲
例3、如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=,AD=1,求DB的长.
【分析】
∵∠ACD=∠ABC,∠A=∠A,
∴△ACD∽△ABC,∴=,
∵AC=,AD=1,
∴=,∴AB=3,
∴DB=AB-AD=3-1=2.
知识精讲
例4、两个相似三角形的最短边分别为5cm和3cm,它们的周长之和为48cm,那么小三角形的周长为( )
A.12cm B.18cm C.24cm D.30cm
【分析】
根据题意,两三角形的周长的比为5:3,
设两三角形的周长分别为5xcm,3xcm,
则5x+3x=48,解得:x=6,
∴3x=18,即小三角形的周长为18cm.
【相似三角形的周长与面积的性质】
B
知识精讲
例5、两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为( )
A.14cm B.16cm C.18cm D.30cm
【分析】
根据题意,两三角形的周长的比为5:3,
设两三角形的周长分别为5xcm,3xcm,
则5x-3x=12,解得:x=6,
∴3x=18,即小三角形的周长为18cm.
C
知识精讲
例6、如图,△ABC∽△A'B'C',AD和A'D'分别是△ABC和△A′B′C′的高,若AD=2,A'D'=3,则△ABC与△A'B'C'的面积的比为( )
A.4:9 B.9:4 C.2:3 D.3:2
C
【分析】
∵△ABC∽△A'B'C',
AD和A'D'分别是△ABC和△A′B′C′的高,AD=2,A'D'=3,
∴==,
∴△ABC与△A'B'C'的面积的比=()2=.
知识精讲
例7、如图,△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2,则下列等式一定成立的是( )
A.=
B.=
C.=
D.=
D
【分析】
∵△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,
∴=,A错误;=,C错误;=,D正确;
不能得出=,B错误.
知识精讲
例8、下列四个命题中,错误的是( )
A.相似三角形对应角平分线的比等于相似比
B.相似三角形面积的比等于对应中线的比的平方
C.相似三角形对应高的比等于对应中线的比
D.相似三角形周长的比等于相似三角形面积的比
【分析】
A、相似三角形对应角平分线的比等于相似比,A√;
B、相似三角形面积的比等于对应中线的比的平方,B√;
C、相似三角形对应高的比等于对应中线的比,C√;
D、相似三角形周长的比等于相似三角形面积的比的算术平方根,D×.
【相似三角形的对应线段的性质】
D
知识精讲
例9、若△ABC∽△DEF,且△ABC与△DEF的面积比是,则△ABC与△DEF对应角平分线之比为________.
【分析】
∵△ABC∽△DEF,△ABC与△DEF的面积比为,
∴△ABC与△DEF的相似比为=,
∴△ABC与△DEF对应角的角平分线之比为.
相似多边形的性质
知识精讲
复习引入
01
Q1:如图,五边形ABCDE~五边形A’B’C’D’E’,我们可以得到什么?
Q2:同样地,相似多边形除了具有对应角相等、对应边成比例的性质外,还具有什么性质?
∵五边形ABCDE~五边形A’B’C’D’E’
∴∠A=∠A’,∠B=∠B’,∠C=∠C’,∠D=∠D’,∠E=∠E’,====
A
B
C
D
E
A’
B’
C’
D’
E’
知识精讲
情境引入
01
问题:如图,如果两个多边形相似,它们的周长有什么关系?
A
B
C
D
E
A’
B’
C’
D’
E’
猜想:类比相似三角形,相似多边形周长的比等于相似比
知识精讲
情境引入
01
证明:∵五边形ABCDE∽五边形A’B’C’D’E’
∴=====k(设相似比为k)
∴AB=kA'B',BC=kB'C',CD=kC'D',DE=kD'E',EA=kE'A'
∴==k
即=k
A
B
C
D
E
A’
B’
C’
D’
E’
知识精讲
情境引入
01
问题:如图,如果两个多边形相似,它们的面积有什么关系?
A
B
C
D
E
A’
B’
C’
D’
E’
猜想:类比相似三角形,相似多边形面积的比等于相似比的平方
知识精讲
情境引入
01
证明思路:
(一)将两幅图中的五边形分别切割成如图的三个三角形
(二)分别证明两幅图中对应的三组三角形相似
(三)将两幅图中五边形的面积转化成对应图中的三个三角形面积之和
由此可得:=相似比2
A
B
C
D
E
A’
B’
C’
D’
E’
02
知识精讲
相似多边形周长的比等于相似比
相似多边形面积的比等于相似比的平方
相似多边形的性质
知识精讲
例10、如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是________.
【相似多边形的对应边的性质】
【分析】
∵四边形ABCD∽四边形A1B1C1D1,
∴=,
∵AB=12,CD=15,A1B1=9,
∴=,解得:C1D1=.
知识精讲
例11、如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )
A.2
B.2.4
C.2.5
D.3
A
【分析】
∵矩形ABCD∽矩形ADFE,
∴=,
∵AE=1,AB=4,
∴=,解得:AD=2.
知识精讲
例12、下列说法错误的是( )
A.若把一个多边形的各边扩大为原来的k倍,则其周长也扩大为原来的k倍
B.若把一个多边形的面积扩大为原来的k倍,则其各边扩大为原来的k2倍
C.相似三角形的对应中线、对应角平分线、对应高的比都等于相似比
D.相似三角形的面积比等于周长比的平方
【相似多边形的周长与面积的性质】
B
【分析】
A.一个多边形的各边扩大为原来的k倍,其周长也扩大为原来的k倍,A√;
B.一个多边形的面积扩大为原来的k倍,其各边扩大为原来的倍,B×;
C.相似三角形的对应中线、对应角平分线、对应高的比都等于相似比,C√;
D.相似三角形的面积比等于周长比的平方,D√.
知识精讲
例13、若两个相似多边形的面积比为9:64,则它们的周长比为( )
A.8:3 B.3:8 C.9:64 D.64:9
B
知识精讲
例14、若两个相似多边形的面积之比为1:4,周长之差为6,则这两个相似多边形的周长分别是__________.
【分析】
∵两个相似多边形的面积之比为1:4,
∴两个相似多边形的周长之比为1:2,
设两个多边形的周长分别为x,x+6,
则x+6=2x,解得:x=6,
∴这两个相似多边形的周长分别是6,12.
6, 12
课后总结
相似三角形 面积的比 等于相似比的平方
周长的比 等于相似比
对应高的比 对应线段的比 对应中线的比 对应角平分线的比
相似多边形周长的比等于相似比
相似多边形面积的比等于相似比的平方
谢谢学习
Thank you for learning
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
