人教版八年级下册16.2 二次根式的乘除(第1课时)课件(共27张PPT)
文档属性
| 名称 | 人教版八年级下册16.2 二次根式的乘除(第1课时)课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 18.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 10:09:34 | ||
图片预览







文档简介
(共27张PPT)
16.2二次根式的乘除(第1课时)
第16章 二次根式
教师
xxx
人教版 八年级下册
二次根式的乘法法则
乘法运算律在二次根式乘法中的应用
积的算术平方根的性质
二次根式乘法的应用
01
03
02
04
CONTANTS
目 录
二次根式的乘法法则
01
学校教学楼后有一长方形花坛(长、宽如图所示,单位:m),现在学校根据需要,想把它改建为草坪.若全部铺满,需购买多少平方米的草皮?
情景引入
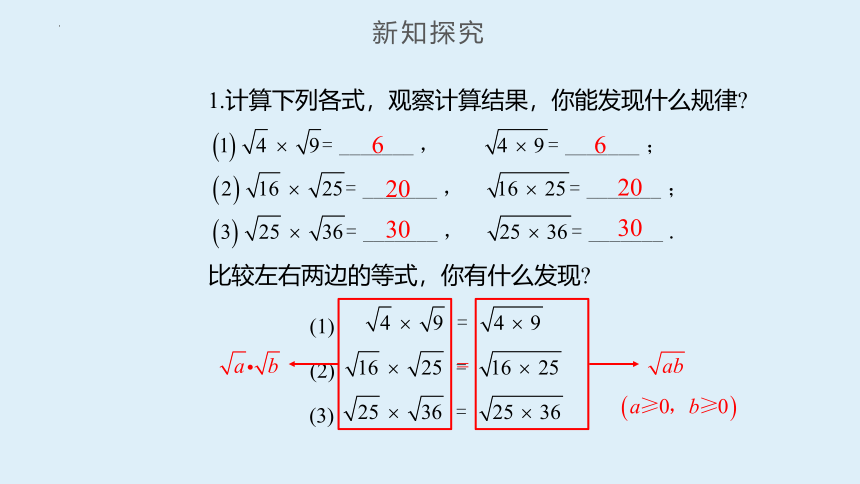
比较左右两边的等式,你有什么发现
6
6
20
20
30
30
1.计算下列各式,观察计算结果,你能发现什么规律
(1)
(2)
(3)
新知探究
2.用上题你所发现的规律填空:
=
思考与交流:在前面所发现的规律表达式 · = 中,a,b可否为任意实数?说明理由.
注意:式中a,b
都必须是非负数.
(1) × _____
;
(2) ×=____________.
新知探究
这就是说,两个算术平方根的积,等于它们被开方数的积的算术平方根.
二次根式的乘法法则
注意:被开方数 a,b 既可以是数,也可以是代数式,但都必须是非负的.
新知探究
例1 计算:
解:
提示:
两个二次根式相乘,把被开方数相乘,根指数不变.即:
典型例题
积的算术平方根的性质
02
反过来,根据二次根式的乘法法则可得
我们可以运用它来进行二次根式的解题和化简.
这就是说,积的算术平方根,等于积中各因式的算术平方根的积.
新知探究
例2 化简:
解:
典型例题
乘法运算律在二次根式乘法中的应用
03
(2).
也就是说,把被开方数和各个根号外面的系数分别相乘,将系数相乘的
积作为积的系数,把被开方数相乘的积作为积的被开方数.
(1);
.
新知探究
例3 计算:
(1);
(3); (4)(-).
解:(1)
(2).
典型例题
例3 计算:
(1);
(3); (4)(-).
解:(3).
(4) (-) =(-2)×.
典型例题
特别提醒:
(1)二次根式相乘时,可利用乘法交换律和结合律,将二次根式根号外的因数(式)和两个二次根式分别相乘,同时注意确定积的符号.
(2)二次根式相乘时,被开方数的积中有能开得尽方的一定要开方.
新知探究
例4 化简:
(1);
(2);
(3) (a≥0,b≥0);
(4) (a<0).
要使得被开方数中不再含有完全平方的因数(或因式)!
典型例题
解:(1)原式= ×=7×11=77.
(2)== ×=4×3=12.
(3)原式=×=a2.
(4)原式=×=-a.
例4 化简:
(1);
(2);
(3) (a≥0,b≥0);
(4) (a<0).
典型例题
例5 计算:
典型例题
例5 计算:
小结:
(1)二次根式相乘时,把被开方数和各个根号外面的系数分别相乘,将系数相乘的积作为积的系数,把被开方数相乘的积作为积的被开方数.
(2)在被开方数相乘时,可以先因数分解或因式分解.
典型例题
3.如果因式中有平方式(或平方数),应用关系式a2 = 把这个因式(或因数)开出来,将二次根式化简 .
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积;
化简二次根式的步骤:
归纳:
新知探究
二次根式乘法的应用
02
例6 一个长方形的长和宽分别是 和2 .求这个长方形的面积.
解:长方形的面积
答:这个长方形的面积为4
典型例题
1.若 , 则( )
A.x≥6 B.x≥0
C.0≤x≤6 D.x为一切实数
A
2.下列运算正确的是 ( )
A.
B.
C.
D.
D
课堂练习
3. 计算:
4.若直角三角形两条直角边的边长分别为 cm和
cm,那么此直角三角形的面积是 cm2.
5.如果 成立,那么x应满足什么条件?
解:由题意得
x+1≥0,
2-x≥0.
所以-1≤ x ≤2
课堂练习
6.计算:
(1);(2);(3).
解:(1).
(2) .
(3).
课堂练习
二次根式
的乘法
一般地,二次根式的乘法法则是
算术平方根的积等于被开方数的积的算术平方根.
乘法法则
积的算术平方根
反过来,可得积的算术平方根的性质
积的算术平方根等于积中各因式的算术平方根的积.
应用
1. 乘法运算律在二次根式乘法中的应用
2. 二次根式乘法的实际应用.
课堂小结
16.2二次根式的乘除(第1课时)
第16章 二次根式
教师
xxx
人教版 八年级下册
二次根式的乘法法则
乘法运算律在二次根式乘法中的应用
积的算术平方根的性质
二次根式乘法的应用
01
03
02
04
CONTANTS
目 录
二次根式的乘法法则
01
学校教学楼后有一长方形花坛(长、宽如图所示,单位:m),现在学校根据需要,想把它改建为草坪.若全部铺满,需购买多少平方米的草皮?
情景引入
比较左右两边的等式,你有什么发现
6
6
20
20
30
30
1.计算下列各式,观察计算结果,你能发现什么规律
(1)
(2)
(3)
新知探究
2.用上题你所发现的规律填空:
=
思考与交流:在前面所发现的规律表达式 · = 中,a,b可否为任意实数?说明理由.
注意:式中a,b
都必须是非负数.
(1) × _____
;
(2) ×=____________.
新知探究
这就是说,两个算术平方根的积,等于它们被开方数的积的算术平方根.
二次根式的乘法法则
注意:被开方数 a,b 既可以是数,也可以是代数式,但都必须是非负的.
新知探究
例1 计算:
解:
提示:
两个二次根式相乘,把被开方数相乘,根指数不变.即:
典型例题
积的算术平方根的性质
02
反过来,根据二次根式的乘法法则可得
我们可以运用它来进行二次根式的解题和化简.
这就是说,积的算术平方根,等于积中各因式的算术平方根的积.
新知探究
例2 化简:
解:
典型例题
乘法运算律在二次根式乘法中的应用
03
(2).
也就是说,把被开方数和各个根号外面的系数分别相乘,将系数相乘的
积作为积的系数,把被开方数相乘的积作为积的被开方数.
(1);
.
新知探究
例3 计算:
(1);
(3); (4)(-).
解:(1)
(2).
典型例题
例3 计算:
(1);
(3); (4)(-).
解:(3).
(4) (-) =(-2)×.
典型例题
特别提醒:
(1)二次根式相乘时,可利用乘法交换律和结合律,将二次根式根号外的因数(式)和两个二次根式分别相乘,同时注意确定积的符号.
(2)二次根式相乘时,被开方数的积中有能开得尽方的一定要开方.
新知探究
例4 化简:
(1);
(2);
(3) (a≥0,b≥0);
(4) (a<0).
要使得被开方数中不再含有完全平方的因数(或因式)!
典型例题
解:(1)原式= ×=7×11=77.
(2)== ×=4×3=12.
(3)原式=×=a2.
(4)原式=×=-a.
例4 化简:
(1);
(2);
(3) (a≥0,b≥0);
(4) (a<0).
典型例题
例5 计算:
典型例题
例5 计算:
小结:
(1)二次根式相乘时,把被开方数和各个根号外面的系数分别相乘,将系数相乘的积作为积的系数,把被开方数相乘的积作为积的被开方数.
(2)在被开方数相乘时,可以先因数分解或因式分解.
典型例题
3.如果因式中有平方式(或平方数),应用关系式a2 = 把这个因式(或因数)开出来,将二次根式化简 .
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积;
化简二次根式的步骤:
归纳:
新知探究
二次根式乘法的应用
02
例6 一个长方形的长和宽分别是 和2 .求这个长方形的面积.
解:长方形的面积
答:这个长方形的面积为4
典型例题
1.若 , 则( )
A.x≥6 B.x≥0
C.0≤x≤6 D.x为一切实数
A
2.下列运算正确的是 ( )
A.
B.
C.
D.
D
课堂练习
3. 计算:
4.若直角三角形两条直角边的边长分别为 cm和
cm,那么此直角三角形的面积是 cm2.
5.如果 成立,那么x应满足什么条件?
解:由题意得
x+1≥0,
2-x≥0.
所以-1≤ x ≤2
课堂练习
6.计算:
(1);(2);(3).
解:(1).
(2) .
(3).
课堂练习
二次根式
的乘法
一般地,二次根式的乘法法则是
算术平方根的积等于被开方数的积的算术平方根.
乘法法则
积的算术平方根
反过来,可得积的算术平方根的性质
积的算术平方根等于积中各因式的算术平方根的积.
应用
1. 乘法运算律在二次根式乘法中的应用
2. 二次根式乘法的实际应用.
课堂小结
