苏教版高中必修一5.1 函数的概念和图象 学案(含答案)
文档属性
| 名称 | 苏教版高中必修一5.1 函数的概念和图象 学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 333.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 11:32:00 | ||
图片预览


文档简介
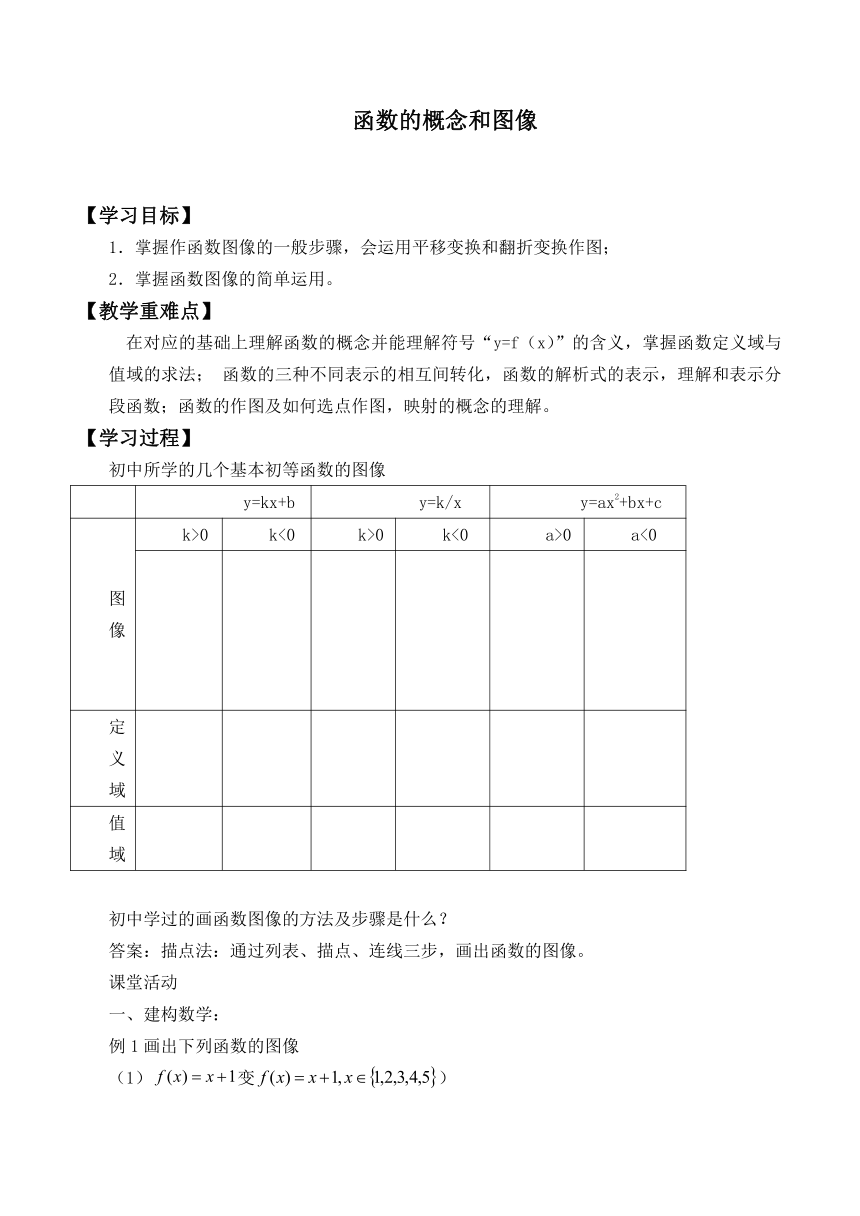
函数的概念和图像
【学习目标】
1.掌握作函数图像的一般步骤,会运用平移变换和翻折变换作图;
2.掌握函数图像的简单运用。
【教学重难点】
在对应的基础上理解函数的概念并能理解符号“y=f(x)”的含义,掌握函数定义域与值域的求法; 函数的三种不同表示的相互间转化,函数的解析式的表示,理解和表示分段函数;函数的作图及如何选点作图,映射的概念的理解。
【学习过程】
初中所学的几个基本初等函数的图像
y=kx+b y=k/x y=ax2+bx+c
图像 k>0 k<0 k>0 k<0 a>0 a<0
定义域
值域
初中学过的画函数图像的方法及步骤是什么?
答案:描点法:通过列表、描点、连线三步,画出函数的图像。
课堂活动
一、建构数学:
例1画出下列函数的图像
(1)变)
(2);(3);
变1: ; 变2:。
小结:函数图像的平移变换:
①水平平移y=f(x±a)(a>0)的图像,可由y=f(x)的图像向左或右平移a个单位得到。
②竖直平移y=f(x)±b(b>0)的图像,可由y=f(x)的图像向上或向下平移b个单位而得到。
例2 (1)画出函数的值;
(2)画出函数;
(3)画出函数。
小结:函数图像的画法:
y=f(|x|)的图像在y轴右侧(x>0)的部分与y=f(x)的图像相同,在y轴左侧部分与其右侧部分关于y轴对称。
例3画出下列函数的图像:
(2) (3)
小结:函数图像的画法:
y=|f(x)|的图像在x轴上方部分与y=f(x)的图像相同,其他部分图像为y=f(x)图像下方部分关于x轴的对称图形。
二、应用数学:
例1 试画出函数的图像,并根据图像回答下列问题:
①比较的大小;
②若
解:(1);
(2)若,则 。
变1:若
变2:
解:若,则;
若,则。
小结:开口向上的二次函数,自变量离对称轴越远其函数值越大。
例2画出下列函数的图像
(1) (2) (3)。
小结:分段函数图像的画法
例3 作函数y=x + 的图像。
拓展:做出y=ax + (a>0,b>0)的示意图。
例4(1)将函数,再向上平移1个单位,得到的函数解析式为__________________________。
将函数的图像向右平移2个单位,再向下平移3个单位,得到的函数解析式为__________________________。
(3)已知函数的定义域为[a,b],值域为[m,n],则函数的定义域为:____________,值域为_______________;函数的定义域为____________,值域为___________________。
三、理解数学:
1.如图为函数f(x)的图像,那么f(x)是下列函数中的 (1) (填序号)。
(1)f(x)=;(2)f(x)=x2-2|x|+1;
(3)f(x)=|x2-1|;(4)f(x)= 。
2.若把函数f(x)的图像作平移变换,使图像上的点P(1,0)变换成点Q(2,-1),则函数y=f(x)的图像经此变换后所得图像的函数解析式为 y=f(x-1)-1 。
3.若,则函数的图像不经过 四 象限。
4.已知函数的图像,那么的图像是 (1) 。
(1) (2) (3) (4) (5)
5.表示和中的较小者,则函数的最大值是 6 。
【达标检测】
1.把函数的图像向右平移2个单位,再向下平移3个单位,所得图像的函数解析式是 。
2.已知函数f(x)= 。
(1)画出函数图像;
(2)求f{f[f(-2)]};
(3)求当f(x)= -7时,x的值。
解:(1)图像略;
(2)f(-2)=2x(-2)+3=-1,f(-1)=( -1)2=1,f(1)=1,
所以f{f[f(-2)]}=1.
(3)因为f(x)= -7,所以2x+3=-7,所以x=-5.
3.求函数的值域。
提示:转化为分段函数求解。
答案:
4.讨论关于的方程的实数解的个数。
解:做出函数图像可知:注意结论形式。
5.的解集为空集,求实数的范围。
答案:。
思考题:
若关于的方程有两个不同的实数解,求实数的取值范围。
提示:换元。
答案:。
【学习目标】
1.掌握作函数图像的一般步骤,会运用平移变换和翻折变换作图;
2.掌握函数图像的简单运用。
【教学重难点】
在对应的基础上理解函数的概念并能理解符号“y=f(x)”的含义,掌握函数定义域与值域的求法; 函数的三种不同表示的相互间转化,函数的解析式的表示,理解和表示分段函数;函数的作图及如何选点作图,映射的概念的理解。
【学习过程】
初中所学的几个基本初等函数的图像
y=kx+b y=k/x y=ax2+bx+c
图像 k>0 k<0 k>0 k<0 a>0 a<0
定义域
值域
初中学过的画函数图像的方法及步骤是什么?
答案:描点法:通过列表、描点、连线三步,画出函数的图像。
课堂活动
一、建构数学:
例1画出下列函数的图像
(1)变)
(2);(3);
变1: ; 变2:。
小结:函数图像的平移变换:
①水平平移y=f(x±a)(a>0)的图像,可由y=f(x)的图像向左或右平移a个单位得到。
②竖直平移y=f(x)±b(b>0)的图像,可由y=f(x)的图像向上或向下平移b个单位而得到。
例2 (1)画出函数的值;
(2)画出函数;
(3)画出函数。
小结:函数图像的画法:
y=f(|x|)的图像在y轴右侧(x>0)的部分与y=f(x)的图像相同,在y轴左侧部分与其右侧部分关于y轴对称。
例3画出下列函数的图像:
(2) (3)
小结:函数图像的画法:
y=|f(x)|的图像在x轴上方部分与y=f(x)的图像相同,其他部分图像为y=f(x)图像下方部分关于x轴的对称图形。
二、应用数学:
例1 试画出函数的图像,并根据图像回答下列问题:
①比较的大小;
②若
解:(1);
(2)若,则 。
变1:若
变2:
解:若,则;
若,则。
小结:开口向上的二次函数,自变量离对称轴越远其函数值越大。
例2画出下列函数的图像
(1) (2) (3)。
小结:分段函数图像的画法
例3 作函数y=x + 的图像。
拓展:做出y=ax + (a>0,b>0)的示意图。
例4(1)将函数,再向上平移1个单位,得到的函数解析式为__________________________。
将函数的图像向右平移2个单位,再向下平移3个单位,得到的函数解析式为__________________________。
(3)已知函数的定义域为[a,b],值域为[m,n],则函数的定义域为:____________,值域为_______________;函数的定义域为____________,值域为___________________。
三、理解数学:
1.如图为函数f(x)的图像,那么f(x)是下列函数中的 (1) (填序号)。
(1)f(x)=;(2)f(x)=x2-2|x|+1;
(3)f(x)=|x2-1|;(4)f(x)= 。
2.若把函数f(x)的图像作平移变换,使图像上的点P(1,0)变换成点Q(2,-1),则函数y=f(x)的图像经此变换后所得图像的函数解析式为 y=f(x-1)-1 。
3.若,则函数的图像不经过 四 象限。
4.已知函数的图像,那么的图像是 (1) 。
(1) (2) (3) (4) (5)
5.表示和中的较小者,则函数的最大值是 6 。
【达标检测】
1.把函数的图像向右平移2个单位,再向下平移3个单位,所得图像的函数解析式是 。
2.已知函数f(x)= 。
(1)画出函数图像;
(2)求f{f[f(-2)]};
(3)求当f(x)= -7时,x的值。
解:(1)图像略;
(2)f(-2)=2x(-2)+3=-1,f(-1)=( -1)2=1,f(1)=1,
所以f{f[f(-2)]}=1.
(3)因为f(x)= -7,所以2x+3=-7,所以x=-5.
3.求函数的值域。
提示:转化为分段函数求解。
答案:
4.讨论关于的方程的实数解的个数。
解:做出函数图像可知:注意结论形式。
5.的解集为空集,求实数的范围。
答案:。
思考题:
若关于的方程有两个不同的实数解,求实数的取值范围。
提示:换元。
答案:。
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
