2013-2014学年青岛版九年级数学上册第2章图形与变换检测题含答案详解
文档属性
| 名称 | 2013-2014学年青岛版九年级数学上册第2章图形与变换检测题含答案详解 |  | |
| 格式 | zip | ||
| 文件大小 | 402.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-04 18:37:26 | ||
图片预览

文档简介
第2章 图形与变换检测题
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.下列汽车标志图案中,能用平移变换来分析形成过程的图案是( )
A B C D
2.如图,△是由△经过平移后得到的,则平移的距离是( )
A.线段BE的长度 B.线段EC的长度 C.线段的长度 D.线段EF的长度
3.同学们曾玩过万花筒吧?如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形可以看成是把菱形以点A为中心( )得到的.
A.顺时针旋转60° B.顺时针旋转120° C.逆时针旋转60° D.逆时针旋转120°
4.如图,点都在方格纸的格点上,若△是由△绕点按逆时针方向旋转得到的,则旋转的角度为( )
A.30° B.45° C.90° D.135°
5.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转改变图形的形状和大小
B.平移和旋转的共同点是改变图形的位置
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
6.如图,四边形和四边形是位似图形,且位似比是,若,则 ( )
A.4 B.6 C.9 D.12
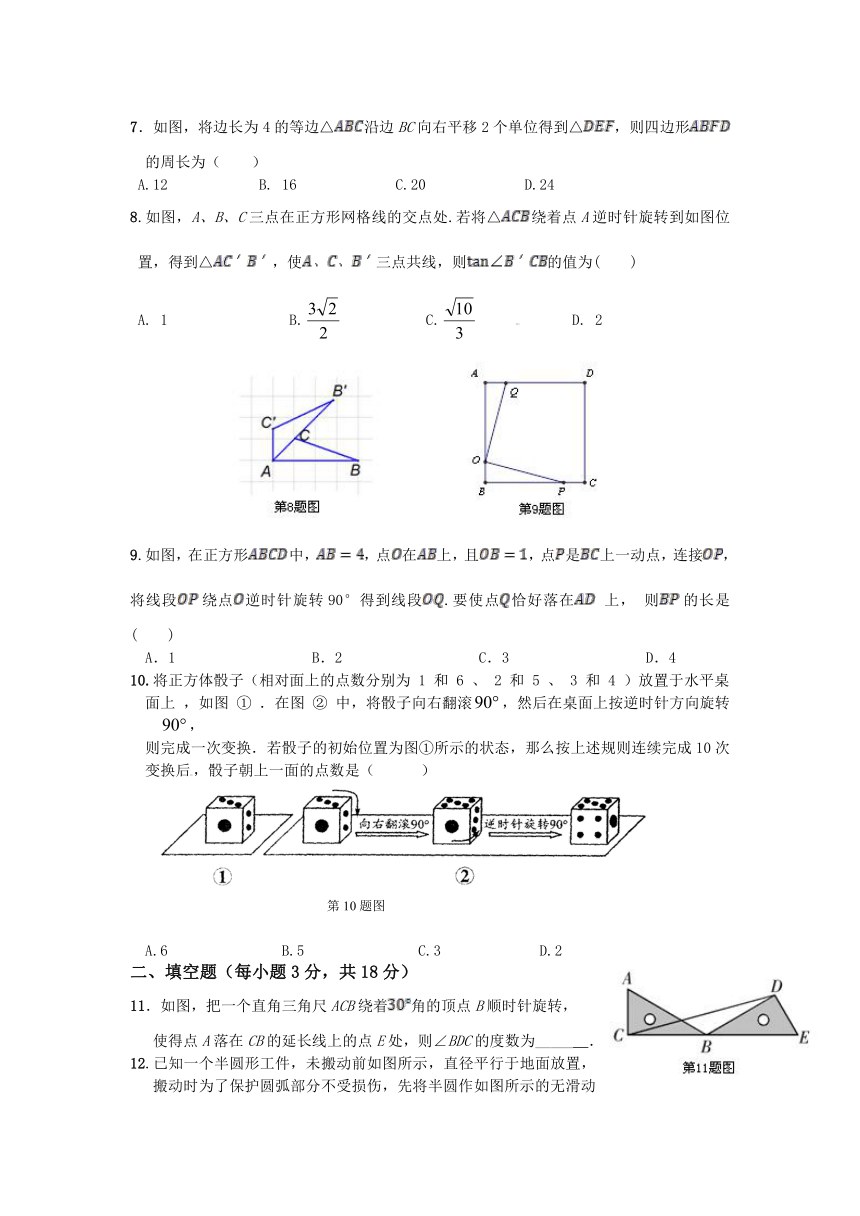
7.如图,将边长为4的等边△沿边BC向右平移2个单位得到△,则四边形的周长为( )
A.12 B. 16 C.20 D.24
8.如图,A、B、C三点在正方形网格线的交点处.若将△绕着点A逆时针旋转到如图位置,得到△,使三点共线,则的值为( )
A. 1 B. C. D. 2
9.如图,在正方形中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转90°得到线段.要使点恰好落在 上, 则的长是( )
A.1 B.2 C.3 D.4
10.将正方体骰子(相对面上的点数分别为 1 和 6 、 2 和 5 、 3 和 4 )放置于水平桌
面上 ,如图 ① .在图 ② 中,将骰子向右翻滚,然后在桌面上按逆时针方向旋转,
则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.2
二、填空题(每小题3分,共18分)
11.如图,把一个直角三角尺ACB绕着角的顶点B顺时针旋转,
使得点A落在CB的延长线上的点E处,则∠BDC的度数为_____ .
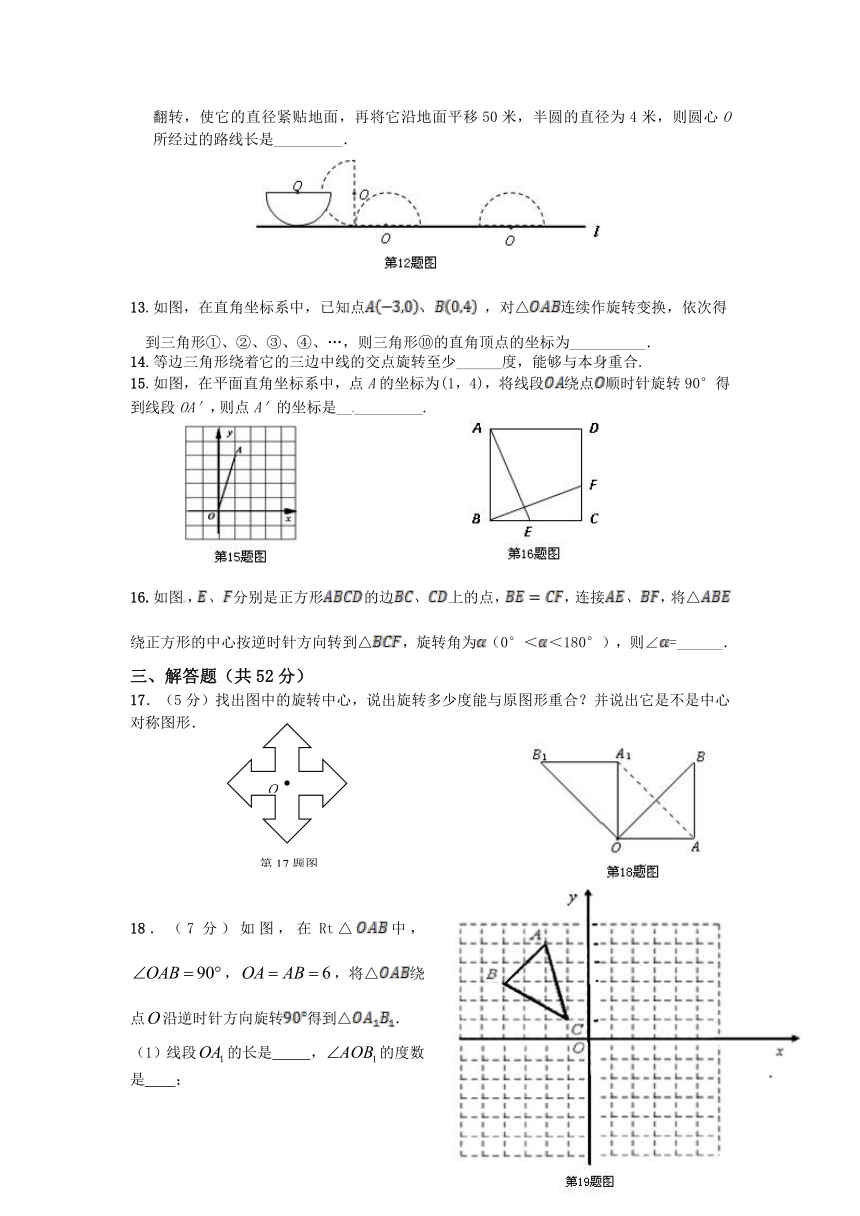
12.已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50米,半圆的直径为4米,则圆心O所经过的路线长是_________.
13.如图,在直角坐标系中,已知点 ,对△连续作旋转变换,依次得
到三角形①、②、③、④、…,则三角形⑩的直角顶点的坐标为__________.
14.等边三角形绕着它的三边中线的交点旋转至少______度,能够与本身重合.
15.如图,在平面直角坐标系中,点A的坐标为(1,4),将线段绕点顺时针旋转90°得到线段OA′,则点A′的坐标是___________.
16.如图,分别是正方形的边上的点,,连接,将△绕正方形的中心按逆时针方向转到△,旋转角为(0°<<180°),则∠=______.
三、解答题(共52分)
17.(5分)找出图中的旋转中心,说出旋转多少度能与原图形重合?并说出它是不是中心对称图形.
18.(7分)如图,在Rt△中,,,将△绕点沿逆时针方向旋转得到△.
(1)线段的长是 ,的度数是 ;
(2)连接,求证:四边形是平行四边形.
19.(8分)如图,在平面直角坐标系中,△的三个顶点的坐标分别为.
(1)作出△向右平移5个单位的
△;
(2)作出△关于轴对称的
△,并写出点的坐标.
20.(8分)如图,网格中有一个四边形和两个三角形.
(1)请你画出三个图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数; 这个整体图形至少旋转多少度与自身重合?
21.(8分)如图,在6×8网格图中,每个小正方形边长均为1,点和△的顶点均在小正方形的顶点上.
(1)以为位似中心,在网格图中作△和△位似,且
位似比为;
(2)连接(1)中的AA′,求四边形的周长(结果保留根号).
22.(8分)如图,是矩形下方一点,将△绕点顺时针旋转60°后,恰好点与点重合,得到△,连接,问△是什么特殊三角形?请说明理由.
23.(8分)如图,将正方形中的△绕对称中心旋转至△的位置,,交于.请猜想与有怎样的数量关系?并证明你的结论.
第2章 图形与变换检测题参考答案
1.D 2.A 3.D
4.C 解析:由旋转到,知旋转角度等于∠的度数,即.
5.B 解析:A.旋转不改变图形的形状和大小;C.图形不可以向某方向旋转一定距离;
D.在旋转图形中,对应线段不一定平行.
6.A 解析:由位似比是32,知所以
7.B 解析:因为, 所以四边形的周长为16.
8.D 解析:过B点作BD⊥于点,由图可知,即=2.
9.C 解析:由题意知,,又由,知△PBO≌△OAQ ,所以BP=OA=AB-OB=3.
10.B 解析:根据规则骰子每变换一次,朝上一面的点数的变化规律是:3(开始)→5→6→3→5→6→3→5→… ,每变换三次为一个循环,所以完成十次变换后,骰子朝上一面的点数是5.
11.15° 解析:由题意得∠,BC=BD ,所以∠.
12.米 解析:.
13.(36,0) 解析:每三次变换为一个循环,直角顶点的横坐标为.
14.120 15.(4,-1) 16.
17.解:图中的旋转中心就是该图形的几何中心,即点O.
该图绕旋转中心O旋转,都能与原来的图形重合,因此,它是一个中心对称图形.
18. (1)解: 6,135°.
(2)证明:,∴.
又,∴ 四边形是平行四边形.
19.解:(1)如图(1);(2)如图(2),点的坐标是.
20.解:(1)如图.
(2)2条对称轴,这个整体图形至少旋转.
21.解:(1)如图.
(2)四边形的周长=4+6.
22.解:△是等边三角形.理由如下:
因为△是将△绕点顺时针旋转60°后得到的,所以△≌△.
因为旋转角度为,所以.
又因为,所以,所以,
所以,所以,所以△是等边三角形.
23.解:.证明如下:
在正方形中,为对角线,为对称中心,
∴.
∵ △为△绕点旋转所得,∴ ,
∴ .
在 △和△中,
∴ △≌△ ,∴ .
第3题图
B
E
A
D
C
F
第2题图
第4题图
C
A
B
D
E
F
G
H
第6题图
第7题图
第10题图
O
第17题图
第20题图
O
第23题图
G
A
C
B
D
E
F
O
N
M
第20题答图
O
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.下列汽车标志图案中,能用平移变换来分析形成过程的图案是( )
A B C D
2.如图,△是由△经过平移后得到的,则平移的距离是( )
A.线段BE的长度 B.线段EC的长度 C.线段的长度 D.线段EF的长度
3.同学们曾玩过万花筒吧?如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形可以看成是把菱形以点A为中心( )得到的.
A.顺时针旋转60° B.顺时针旋转120° C.逆时针旋转60° D.逆时针旋转120°
4.如图,点都在方格纸的格点上,若△是由△绕点按逆时针方向旋转得到的,则旋转的角度为( )
A.30° B.45° C.90° D.135°
5.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转改变图形的形状和大小
B.平移和旋转的共同点是改变图形的位置
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
6.如图,四边形和四边形是位似图形,且位似比是,若,则 ( )
A.4 B.6 C.9 D.12
7.如图,将边长为4的等边△沿边BC向右平移2个单位得到△,则四边形的周长为( )
A.12 B. 16 C.20 D.24
8.如图,A、B、C三点在正方形网格线的交点处.若将△绕着点A逆时针旋转到如图位置,得到△,使三点共线,则的值为( )
A. 1 B. C. D. 2
9.如图,在正方形中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转90°得到线段.要使点恰好落在 上, 则的长是( )
A.1 B.2 C.3 D.4
10.将正方体骰子(相对面上的点数分别为 1 和 6 、 2 和 5 、 3 和 4 )放置于水平桌
面上 ,如图 ① .在图 ② 中,将骰子向右翻滚,然后在桌面上按逆时针方向旋转,
则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.2
二、填空题(每小题3分,共18分)
11.如图,把一个直角三角尺ACB绕着角的顶点B顺时针旋转,
使得点A落在CB的延长线上的点E处,则∠BDC的度数为_____ .
12.已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50米,半圆的直径为4米,则圆心O所经过的路线长是_________.
13.如图,在直角坐标系中,已知点 ,对△连续作旋转变换,依次得
到三角形①、②、③、④、…,则三角形⑩的直角顶点的坐标为__________.
14.等边三角形绕着它的三边中线的交点旋转至少______度,能够与本身重合.
15.如图,在平面直角坐标系中,点A的坐标为(1,4),将线段绕点顺时针旋转90°得到线段OA′,则点A′的坐标是___________.
16.如图,分别是正方形的边上的点,,连接,将△绕正方形的中心按逆时针方向转到△,旋转角为(0°<<180°),则∠=______.
三、解答题(共52分)
17.(5分)找出图中的旋转中心,说出旋转多少度能与原图形重合?并说出它是不是中心对称图形.
18.(7分)如图,在Rt△中,,,将△绕点沿逆时针方向旋转得到△.
(1)线段的长是 ,的度数是 ;
(2)连接,求证:四边形是平行四边形.
19.(8分)如图,在平面直角坐标系中,△的三个顶点的坐标分别为.
(1)作出△向右平移5个单位的
△;
(2)作出△关于轴对称的
△,并写出点的坐标.
20.(8分)如图,网格中有一个四边形和两个三角形.
(1)请你画出三个图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数; 这个整体图形至少旋转多少度与自身重合?
21.(8分)如图,在6×8网格图中,每个小正方形边长均为1,点和△的顶点均在小正方形的顶点上.
(1)以为位似中心,在网格图中作△和△位似,且
位似比为;
(2)连接(1)中的AA′,求四边形的周长(结果保留根号).
22.(8分)如图,是矩形下方一点,将△绕点顺时针旋转60°后,恰好点与点重合,得到△,连接,问△是什么特殊三角形?请说明理由.
23.(8分)如图,将正方形中的△绕对称中心旋转至△的位置,,交于.请猜想与有怎样的数量关系?并证明你的结论.
第2章 图形与变换检测题参考答案
1.D 2.A 3.D
4.C 解析:由旋转到,知旋转角度等于∠的度数,即.
5.B 解析:A.旋转不改变图形的形状和大小;C.图形不可以向某方向旋转一定距离;
D.在旋转图形中,对应线段不一定平行.
6.A 解析:由位似比是32,知所以
7.B 解析:因为, 所以四边形的周长为16.
8.D 解析:过B点作BD⊥于点,由图可知,即=2.
9.C 解析:由题意知,,又由,知△PBO≌△OAQ ,所以BP=OA=AB-OB=3.
10.B 解析:根据规则骰子每变换一次,朝上一面的点数的变化规律是:3(开始)→5→6→3→5→6→3→5→… ,每变换三次为一个循环,所以完成十次变换后,骰子朝上一面的点数是5.
11.15° 解析:由题意得∠,BC=BD ,所以∠.
12.米 解析:.
13.(36,0) 解析:每三次变换为一个循环,直角顶点的横坐标为.
14.120 15.(4,-1) 16.
17.解:图中的旋转中心就是该图形的几何中心,即点O.
该图绕旋转中心O旋转,都能与原来的图形重合,因此,它是一个中心对称图形.
18. (1)解: 6,135°.
(2)证明:,∴.
又,∴ 四边形是平行四边形.
19.解:(1)如图(1);(2)如图(2),点的坐标是.
20.解:(1)如图.
(2)2条对称轴,这个整体图形至少旋转.
21.解:(1)如图.
(2)四边形的周长=4+6.
22.解:△是等边三角形.理由如下:
因为△是将△绕点顺时针旋转60°后得到的,所以△≌△.
因为旋转角度为,所以.
又因为,所以,所以,
所以,所以,所以△是等边三角形.
23.解:.证明如下:
在正方形中,为对角线,为对称中心,
∴.
∵ △为△绕点旋转所得,∴ ,
∴ .
在 △和△中,
∴ △≌△ ,∴ .
第3题图
B
E
A
D
C
F
第2题图
第4题图
C
A
B
D
E
F
G
H
第6题图
第7题图
第10题图
O
第17题图
第20题图
O
第23题图
G
A
C
B
D
E
F
O
N
M
第20题答图
O
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
