2022-2023学年广西贵港市港北区八年级(上)期中数学试卷 (含解析)
文档属性
| 名称 | 2022-2023学年广西贵港市港北区八年级(上)期中数学试卷 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 479.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 08:56:04 | ||
图片预览




文档简介
2022-2023学年广西贵港市港北区八年级(上)期中数学试卷
一、选择题(本题12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑)
1.(3分)在式子,,,中,分式的个数有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)在△ABC中,且满足∠A+∠B=90°,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.(3分)若分式的值为0,则x的值为( )
A.1 B.2 C.﹣1 D.
4.(3分)已知等腰三角形底边和腰的长分别为6和5,则这个等腰三角形的周长为( )
A.15 B.16 C.17 D.18
5.(3分)解分式方程,分以下四步,其中,错误的一步是( )
A.方程两边分式的最简公分母是(x﹣1)(x+1)
B.方程两边都乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6
C.解这个整式方程,得x=1
D.原方程的解为x=1
6.(3分)如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
7.(3分)已知,则的值是( )
A.66 B.64 C.62 D.60
8.(3分)下列命题中,是假命题的是( )
A.全等三角形的对应边相等
B.三角形的一个外角大于任何一个内角
C.有一个角等于60°的等腰三角形是等边三角形
D.一个数的立方根等于他本身,则这个数是﹣1,0,1
9.(3分)如果用换元法解分式方程,并设,那么原方程可化为( )
A. B. C. D.y+
10.(3分)如图,DE,DF分别是线段AB,BC的垂直平分线,连接AD,CD,则下列结论正确的是( )
A.AD=CD B.∠A=∠C C.∠B=∠ADC D.DE=DF
11.(3分)甲、乙两人完成一项工作,甲先做了3天,然后乙加入合作,完成剩下的工作,设工作总量为1,工作进度如表:
天数 第3天 第5天
工作进度
若乙单独完成这项工作,则需要( )
A.9天 B.10天 C.12天 D.24天
12.(3分)如图,在△ABC和△ADE中,∠CAB=∠DAE=36°,AB=AC,AD=AE.连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分∠ABC,则下列结论错误的是( )
A.∠ADC=∠AEB B.CD∥AB C.DE=GE D.CD=BE
二、填空题(本大题共6小题,每小题3分,共18分)
13.(3分)分式没有意义,则x的值为 .
14.(3分)人体细胞的平均直径为0.000105微米,用科学记数法可表示为 微米.
15.(3分)如图,l1∥l2,AE⊥BE于点E.若∠2=140°,则∠1的度数为 .
16.(3分)如图,点P在等边三角形ABC的内部,PD⊥BC,PE⊥AC,PF⊥AB,垂足分别为D,E,F,若PD+PE+PF=4,且S△ABC=16,则△ABC的边长为 .
17.(3分)对于非零的两个实数a,b,规定a*b=,若5*(3x﹣1)=2,则x的值为 .
18.(3分)如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm的速度沿BC向点C运动,点Q从点C出发,以vcm/s的速度沿CA向点A运动,当v= 时,△ABP与△PQC全等.
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
19.(6分)计算.
20.(6分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图,∠α,和线段a.求作:Rt△ABC,使∠BAC=∠α,∠ACB=90°,斜边AB=a.
21.(10分)(1)计算:÷+.
(2)解方程.
22.(6分)如图,在△ABC中,AB=AC,D是BC边上一点,EF垂直平分CD,交AC于点E,交BC于点F,连接DE.若∠A=56°,求∠DEC的度数.
23.(8分)阅读理解题.
(1)观察:,,……,填空:= ;
(2)填空:= ;
(3)利用上述规律解分式方程:.
24.(8分)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.
25.(10分)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米?
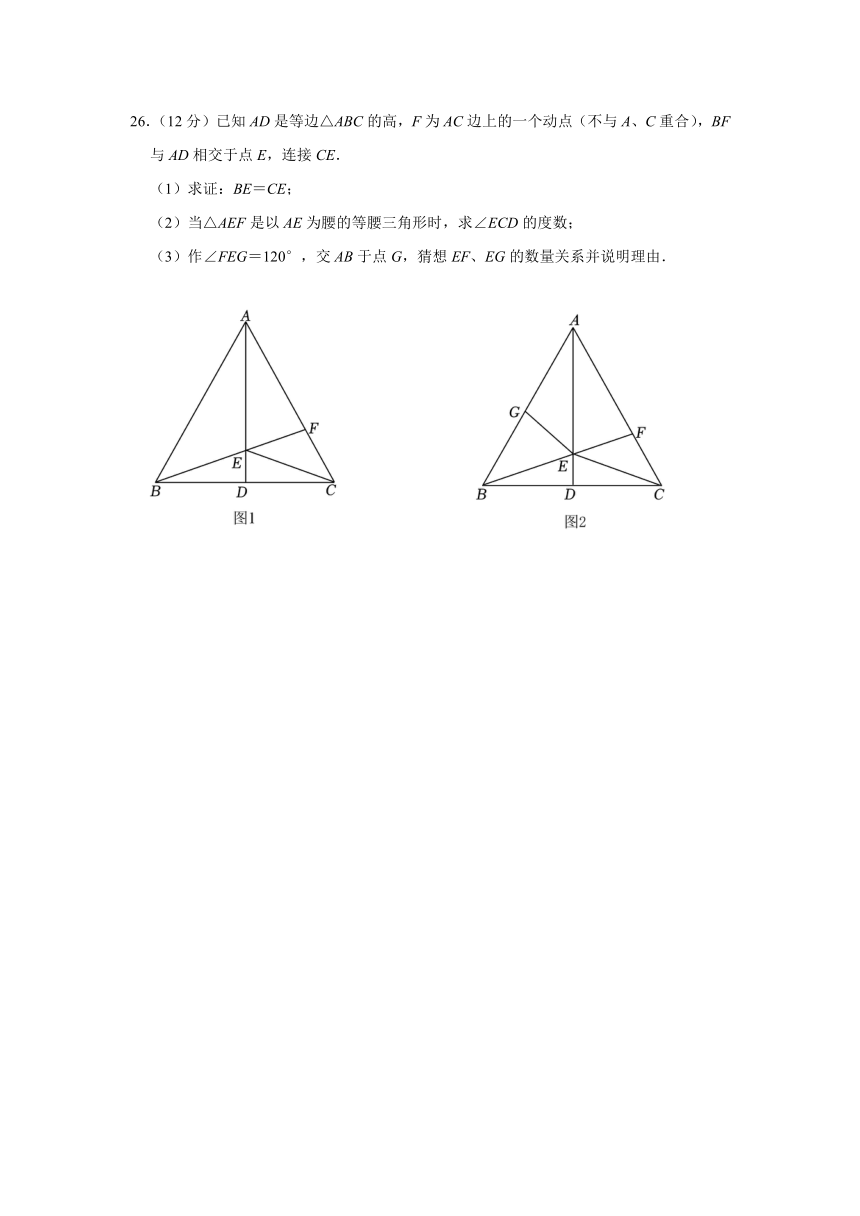
26.(12分)已知AD是等边△ABC的高,F为AC边上的一个动点(不与A、C重合),BF与AD相交于点E,连接CE.
(1)求证:BE=CE;
(2)当△AEF是以AE为腰的等腰三角形时,求∠ECD的度数;
(3)作∠FEG=120°,交AB于点G,猜想EF、EG的数量关系并说明理由.
2022-2023学年广西贵港市港北区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑)
1.(3分)在式子,,,中,分式的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】一般地,如果A,B表示两个整式,并且B中含有字母,那么式子叫做分式,根据分式的定义解答即可.
【解答】解:在式子,,,中,分式是,,
故分式有2个.
故选:B.
2.(3分)在△ABC中,且满足∠A+∠B=90°,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【分析】根据三角形内角和等于180°,可得∠C=180°﹣(∠A+∠B)=90°.据此可得三角形是直角三角形.
【解答】解:在△ABC中,∠A+∠B=90°,
∴∠C=180°﹣(∠A+∠B)=90°.
∴△ABC是直角三角形.
故选:B.
3.(3分)若分式的值为0,则x的值为( )
A.1 B.2 C.﹣1 D.
【分析】根据分式值为零的条件,可得:x+1=0且2x﹣1≠0,据此求出x的值即可.
【解答】解:∵分式的值为0,
∴x+1=0且2x﹣1≠0,
解得:x=﹣1.
故选:C.
4.(3分)已知等腰三角形底边和腰的长分别为6和5,则这个等腰三角形的周长为( )
A.15 B.16 C.17 D.18
【分析】根据等腰三角形的定义求周长即可得出答案.
【解答】解:6+5+5=16,
故选:B.
5.(3分)解分式方程,分以下四步,其中,错误的一步是( )
A.方程两边分式的最简公分母是(x﹣1)(x+1)
B.方程两边都乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6
C.解这个整式方程,得x=1
D.原方程的解为x=1
【分析】分式方程两边乘以最简公分母,去分母转化为整式方程,求出整式方程的解,经检验即可得到分式方程的解.
【解答】解:分式方程的最简公分母为(x﹣1)(x+1),
方程两边乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6,
解得:x=1,
经检验x=1是增根,分式方程无解.
故选:D.
6.(3分)如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出即可.
【解答】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:D.
7.(3分)已知,则的值是( )
A.66 B.64 C.62 D.60
【分析】原式利用完全平方公式变形,将已知等式代入计算即可求出值.
【解答】解:∵x+=8,
∴原式=(x+)2﹣2=64﹣2=62.
故选:C.
8.(3分)下列命题中,是假命题的是( )
A.全等三角形的对应边相等
B.三角形的一个外角大于任何一个内角
C.有一个角等于60°的等腰三角形是等边三角形
D.一个数的立方根等于他本身,则这个数是﹣1,0,1
【分析】根据全等三角形的性质,三角形的外角的性质,等边三角形的判定,立方根的定义一一判断即可.
【解答】解:A、全等三角形的对应边相等,是真命题,本选项不符合题意;
B、三角形的一个外角大于任何一个内角,是假命题,应该是三角形的一个外角大于任何和 它不相邻一个内角,本选项符合题意;
C、有一个角等于60°的等腰三角形是等边三角形,是真命题,本选项不符合题意;
D、一个数的立方根等于它本身,则这个数是﹣1,0,1,是真命题,本选项不符合题意.
故选:B.
9.(3分)如果用换元法解分式方程,并设,那么原方程可化为( )
A. B. C. D.y+
【分析】设,则=,再把方程变形求解.
【解答】解:设,
原方程可化为:y﹣+3=0,
故选:B.
10.(3分)如图,DE,DF分别是线段AB,BC的垂直平分线,连接AD,CD,则下列结论正确的是( )
A.AD=CD B.∠A=∠C C.∠B=∠ADC D.DE=DF
【分析】根据线段垂直平分线的性质得出AD=BD,CD=BD,求出AD=BD=CD,根据等边对等角得出∠A=∠2,∠1=∠C,再逐个判断即可.
【解答】解:连接BD,如图1,
∵DE,DF分别是线段AB,BC的垂直平分线,
∴AD=BD,CD=BD,
即AD=BD=CD,
∴∠A=∠2,∠1=∠C,
不能推出∠A和∠C相等,∠ABC和∠ADC相等,DE和DF相等,
故选:A.
11.(3分)甲、乙两人完成一项工作,甲先做了3天,然后乙加入合作,完成剩下的工作,设工作总量为1,工作进度如表:
天数 第3天 第5天
工作进度
若乙单独完成这项工作,则需要( )
A.9天 B.10天 C.12天 D.24天
【分析】求出甲单独完成这项工程所需时间,设乙单独完成这项工作需x天,根据甲完成的部分+乙完成的部分=这项工程的,列出分式方程,解方程即可.
【解答】解:甲单独完成这项工作所需天数为3÷=12(天).
设乙单独完成这项工作需x天,
依题意,得:+=,
解得:x=24
经检验,x=24是原方程的解,且符合题意.
故选:D.
12.(3分)如图,在△ABC和△ADE中,∠CAB=∠DAE=36°,AB=AC,AD=AE.连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分∠ABC,则下列结论错误的是( )
A.∠ADC=∠AEB B.CD∥AB C.DE=GE D.CD=BE
【分析】利用AAS证明△DAC≌△EAB可得∠ADC=∠AEB,CD=BE,可判断A,D选项正确;由全等三角形的性质,三角形的内角和定理及等腰三角形的性质可求解∠ACB的度数,利用角平分线的定义求得∠ACD=∠ABE=36°,即可得∠ACD=∠CAB,进而可证明CD∥AB,即可判断B选项正确,进而可求解.
【解答】解:A.∵∠CAB=∠DAE=36°,
∴∠CAB﹣∠CAE=∠DAE﹣∠CAE,即∠DAC=∠EAB,
在△DAC和△EAB中,
,
∴△DAC≌△EAB(SAS),
∴∠ADC=∠AEB,故A选项不符合题意;
CD=BE,故D选项不符合题意;
B.∵AC=AB,
∴∠ACB=∠ABC,
∵∠CAB=∠DAE=36°,
∴∠ACB=∠ABC=(180°﹣36°)÷2=72°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=36°,
∴∠ACD=∠ABE=36,
∵∠DCA=∠CAB=36°,
∴CD∥AB(内错角相等,两直线平行),
故B选项不符合题意;
C.根据已知条件无法证明DE=GE,故C选项符合题意.
故选:C.
二、填空题(本大题共6小题,每小题3分,共18分)
13.(3分)分式没有意义,则x的值为 1 .
【分析】根据分式有意义的条件即可求出答案.
【解答】解:当2x﹣2=0时,此时分式无意义,
∴x=1,
故答案为:x=1.
14.(3分)人体细胞的平均直径为0.000105微米,用科学记数法可表示为 1.05×10﹣4 微米.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:0.000105微米=1.05×10﹣4微米.
故答案为:1.05×10﹣4.
15.(3分)如图,l1∥l2,AE⊥BE于点E.若∠2=140°,则∠1的度数为 130° .
【分析】根据平角的定义得出∠4=40°,根据平行线的性质得出∠3=∠4,由垂直的定义求出∠AEB的度数,最后根据三角形外角的性质得出∠1的度数.
【解答】解:如图:
∵∠2=140°,∠4+∠2=180°,
∴∠4=180°﹣∠2=40°,
∵AE⊥BE,
∴∠AEB=90°.
∵l1∥l2,
∴∠3=∠4=40°,
∴∠1=∠3+∠AEB=40°+90°=130°.
故答案为:130°.
16.(3分)如图,点P在等边三角形ABC的内部,PD⊥BC,PE⊥AC,PF⊥AB,垂足分别为D,E,F,若PD+PE+PF=4,且S△ABC=16,则△ABC的边长为 8 .
【分析】连接AP,BP,PC,根据S△ABC=AB×PF+×AC×PE+BC×PD=×AB×(PF+PE+PD),求解即可.
【解答】解:连接AP,BP,PC,
∵△ABC是等边三角形,
∴AB=BC=AC,
∵S△ABC=AB×PF+×AC×PE+BC×PD=×AB×(PF+PE+PD)=16,PD+PE+PF=4
∴AB=8,
故答案为8.
17.(3分)对于非零的两个实数a,b,规定a*b=,若5*(3x﹣1)=2,则x的值为 .
【分析】根据规定,把5*(3x﹣1)=2,转化为我们学过的方程,再求解即可.
【解答】解:∵a*b=,5*(3x﹣1)=2,
∴﹣=2,
去分母得,15﹣2(3x﹣1)=10(3x﹣1),
整理得,36x=27,
解得x=,
经检验,x=是原方程的解,
故答案为.
18.(3分)如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm的速度沿BC向点C运动,点Q从点C出发,以vcm/s的速度沿CA向点A运动,当v= 4或4.8 时,△ABP与△PQC全等.
【分析】分两种情况①当BP=CQ,AB=PC时,△ABP≌△PCQ;②当BA=CQ,PB=PC时,△ABP≌△QCP,然后分别计算出t的值,进而得到v的值.
【解答】解:设运动时间为t秒,
∵点P从点B出发,以2cm的速度沿BC向点C运动,点Q从点C出发,以vcm/s的速度沿CA向点A运动,
∴BP=2t(cm),CQ=vt(cm),
∴PC=10﹣2t(cm),
∵AB=AC,
∴∠B=∠C,
当BP=CQ,AB=PC时,△ABP≌△PCQ,
∴AB=PC=6cm,
∴BP=4cm=CQ,
∴2t=4,
解得:t=2,
∴v==2;
②当BA=CQ=6cm,PB=PC时,△ABP≌△QCP,
∵PB=PC,
∴BP=PC=BC=5cm,
∴2t=5,
解得:t=2.5,
∴v==2.4,
解得:v=2.4,
综上所述:当v=2或2.4时△ABP与△PQC全等,
故答案为:2或2.4.
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
19.(6分)计算.
【分析】根据有理数的乘方、零指数幂、负整数指数幂以及绝对值的性质分别进行计算,即可得出答案.
【解答】解:
=﹣1+1+2﹣3
=﹣1.
20.(6分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图,∠α,和线段a.求作:Rt△ABC,使∠BAC=∠α,∠ACB=90°,斜边AB=a.
【分析】先作∠MAN=∠α,再在AM上截取AB=a,然后过B点作AN的垂线,垂足为C点,则△ABC满足条件.
【解答】解:如图,Rt△ABC为所作.
21.(10分)(1)计算:÷+.
(2)解方程.
【分析】(1)原式利用除法法则变形,约分后利用同分母分式的加法法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:(1)原式= (a+1)(a﹣1)+=+==2;
(2)去分母得:x﹣3+x﹣2=3,
解得:x=4,
经检验x=4是分式方程的解.
22.(6分)如图,在△ABC中,AB=AC,D是BC边上一点,EF垂直平分CD,交AC于点E,交BC于点F,连接DE.若∠A=56°,求∠DEC的度数.
【分析】根据线段垂直平分线的性质可得∠EDC=∠ECD,根据等腰三角形的性质进一步可得∠EDC=∠ABC,根据平行线的性质可得∠DEC的度数,根据等腰三角形的性质即可求出∠DEF的度数.
【解答】解:∵EF垂直平分CD,
∴ED=EC,
∴∠EDC=∠ECD,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EDC=∠ABC,
∴DE∥AB;
∵DE∥AB,∠A=56°,
∴∠DEC=∠A=56°,
23.(8分)阅读理解题.
(1)观察:,,……,填空:= ﹣ ;
(2)填空:= ;
(3)利用上述规律解分式方程:.
【分析】(1)根据前三个式子的结果直接写出答案;
(2)根据以上等式的规律直接写出答案;
(3)根据规律变形,然后解分式方程即可.
【解答】解:(1)=﹣;
故答案为:﹣;
(2)
=1﹣+﹣+…+﹣
=1﹣
=,
故答案为:;
(3),
1﹣=2﹣,
去分母得:x+1﹣1=2x+2﹣7
解得:x=5,
经检验:x=5是方程的根,
∴原方程的解为x=5.
24.(8分)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.
【分析】先猜想AP=CQ,再在△ABP与△CBQ中,由AB=CB,BP=BQ,∠ABC=∠PBQ=60°可得出∠ABP=∠CBQ,进而可判断出△ABP≌△CBQ,由全等三角形的对应边相等即可得出结论.
【解答】猜想:AP=CQ
证明:在△ABP与△CBQ中,
∵AB=CB,BP=BQ,∠ABC=∠PBQ=60°,
∴∠ABP=∠ABC﹣∠PBC=∠PBQ﹣∠PBC=∠CBQ,
∴△ABP≌△CBQ,
∴AP=CQ
25.(10分)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米?
【分析】(1)根据题意可知:甲原来工作5天的工作量+后来2天的工作量=600,可以列出相应的方程,然后求解即可;
(2)根据题意可知:甲、乙施工的长度都是900米,再根据题意可知,两个工程队施工天数相同,即可列出相应的分式方程,然后求解即可,注意分式方程要检验.
【解答】解:(1)设甲施工队增加人员后每天修建灌溉水渠x米,则原计划每天施工(x﹣20)米,
由题意可得:5(x﹣20)+2x=600,
解得x=100,
答:甲施工队增加人员后每天修建灌溉水渠100米;
(2)设乙施工队原来每天修建灌溉水渠m米,则技术更新后每天修建水渠m(1+20%)=1.2m米,
由题意可得:,
解得m=90,
经检验,m=90是原分式方程的解,
答:乙施工队原来每天修建灌溉水渠90米.
26.(12分)已知AD是等边△ABC的高,F为AC边上的一个动点(不与A、C重合),BF与AD相交于点E,连接CE.
(1)求证:BE=CE;
(2)当△AEF是以AE为腰的等腰三角形时,求∠ECD的度数;
(3)作∠FEG=120°,交AB于点G,猜想EF、EG的数量关系并说明理由.
【分析】(1)先判断出AD是BC的垂直平分线,即可得出结论;
(2)先判断出等腰三角形AEF的腰,再用等腰三角形的性质和三角形的外角的性质即可得出结论;
(3)先判断出,∠AFE=BGE,进而构造出全等三角形,即可得出结论.
【解答】(1)证明:∵AD是等边△ABC的高,
∴AD是BC的垂直平分线,
∵点E在AD上,
∴BE=CE;
(2)解:∵AD是等边△ABC的高,
∴∠CAD=∠BAC=30°,
∵△AEF为等腰三角形,AE为腰,
∴AE=AF,
∴∠AEF=∠AFE=75°,
∵∠ACB=60°,
∴∠CBF=∠AFE﹣∠ACB=75°﹣60°=15°,
∵BE=CE,
∴∠ECD=∠CBF=15°;
(3)解:结论:EF=EG,
理由:∵∠BAC=60°,∠FEG=120°,
∴∠BAC+∠FEG=180°,
∴∠AGE+∠AFE=180°,
∴∠AFE=BGE,
过点E作EN⊥AB,EM⊥AC,
∵AD是∠BAC的平分线,
∴EN=EM;
在△ENG和△EMF中,
,
∴△ENG≌△EMF,
∴EG=EF.
一、选择题(本题12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑)
1.(3分)在式子,,,中,分式的个数有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)在△ABC中,且满足∠A+∠B=90°,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.(3分)若分式的值为0,则x的值为( )
A.1 B.2 C.﹣1 D.
4.(3分)已知等腰三角形底边和腰的长分别为6和5,则这个等腰三角形的周长为( )
A.15 B.16 C.17 D.18
5.(3分)解分式方程,分以下四步,其中,错误的一步是( )
A.方程两边分式的最简公分母是(x﹣1)(x+1)
B.方程两边都乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6
C.解这个整式方程,得x=1
D.原方程的解为x=1
6.(3分)如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
7.(3分)已知,则的值是( )
A.66 B.64 C.62 D.60
8.(3分)下列命题中,是假命题的是( )
A.全等三角形的对应边相等
B.三角形的一个外角大于任何一个内角
C.有一个角等于60°的等腰三角形是等边三角形
D.一个数的立方根等于他本身,则这个数是﹣1,0,1
9.(3分)如果用换元法解分式方程,并设,那么原方程可化为( )
A. B. C. D.y+
10.(3分)如图,DE,DF分别是线段AB,BC的垂直平分线,连接AD,CD,则下列结论正确的是( )
A.AD=CD B.∠A=∠C C.∠B=∠ADC D.DE=DF
11.(3分)甲、乙两人完成一项工作,甲先做了3天,然后乙加入合作,完成剩下的工作,设工作总量为1,工作进度如表:
天数 第3天 第5天
工作进度
若乙单独完成这项工作,则需要( )
A.9天 B.10天 C.12天 D.24天
12.(3分)如图,在△ABC和△ADE中,∠CAB=∠DAE=36°,AB=AC,AD=AE.连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分∠ABC,则下列结论错误的是( )
A.∠ADC=∠AEB B.CD∥AB C.DE=GE D.CD=BE
二、填空题(本大题共6小题,每小题3分,共18分)
13.(3分)分式没有意义,则x的值为 .
14.(3分)人体细胞的平均直径为0.000105微米,用科学记数法可表示为 微米.
15.(3分)如图,l1∥l2,AE⊥BE于点E.若∠2=140°,则∠1的度数为 .
16.(3分)如图,点P在等边三角形ABC的内部,PD⊥BC,PE⊥AC,PF⊥AB,垂足分别为D,E,F,若PD+PE+PF=4,且S△ABC=16,则△ABC的边长为 .
17.(3分)对于非零的两个实数a,b,规定a*b=,若5*(3x﹣1)=2,则x的值为 .
18.(3分)如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm的速度沿BC向点C运动,点Q从点C出发,以vcm/s的速度沿CA向点A运动,当v= 时,△ABP与△PQC全等.
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
19.(6分)计算.
20.(6分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图,∠α,和线段a.求作:Rt△ABC,使∠BAC=∠α,∠ACB=90°,斜边AB=a.
21.(10分)(1)计算:÷+.
(2)解方程.
22.(6分)如图,在△ABC中,AB=AC,D是BC边上一点,EF垂直平分CD,交AC于点E,交BC于点F,连接DE.若∠A=56°,求∠DEC的度数.
23.(8分)阅读理解题.
(1)观察:,,……,填空:= ;
(2)填空:= ;
(3)利用上述规律解分式方程:.
24.(8分)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.
25.(10分)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米?
26.(12分)已知AD是等边△ABC的高,F为AC边上的一个动点(不与A、C重合),BF与AD相交于点E,连接CE.
(1)求证:BE=CE;
(2)当△AEF是以AE为腰的等腰三角形时,求∠ECD的度数;
(3)作∠FEG=120°,交AB于点G,猜想EF、EG的数量关系并说明理由.
2022-2023学年广西贵港市港北区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑)
1.(3分)在式子,,,中,分式的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】一般地,如果A,B表示两个整式,并且B中含有字母,那么式子叫做分式,根据分式的定义解答即可.
【解答】解:在式子,,,中,分式是,,
故分式有2个.
故选:B.
2.(3分)在△ABC中,且满足∠A+∠B=90°,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【分析】根据三角形内角和等于180°,可得∠C=180°﹣(∠A+∠B)=90°.据此可得三角形是直角三角形.
【解答】解:在△ABC中,∠A+∠B=90°,
∴∠C=180°﹣(∠A+∠B)=90°.
∴△ABC是直角三角形.
故选:B.
3.(3分)若分式的值为0,则x的值为( )
A.1 B.2 C.﹣1 D.
【分析】根据分式值为零的条件,可得:x+1=0且2x﹣1≠0,据此求出x的值即可.
【解答】解:∵分式的值为0,
∴x+1=0且2x﹣1≠0,
解得:x=﹣1.
故选:C.
4.(3分)已知等腰三角形底边和腰的长分别为6和5,则这个等腰三角形的周长为( )
A.15 B.16 C.17 D.18
【分析】根据等腰三角形的定义求周长即可得出答案.
【解答】解:6+5+5=16,
故选:B.
5.(3分)解分式方程,分以下四步,其中,错误的一步是( )
A.方程两边分式的最简公分母是(x﹣1)(x+1)
B.方程两边都乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6
C.解这个整式方程,得x=1
D.原方程的解为x=1
【分析】分式方程两边乘以最简公分母,去分母转化为整式方程,求出整式方程的解,经检验即可得到分式方程的解.
【解答】解:分式方程的最简公分母为(x﹣1)(x+1),
方程两边乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6,
解得:x=1,
经检验x=1是增根,分式方程无解.
故选:D.
6.(3分)如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出即可.
【解答】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:D.
7.(3分)已知,则的值是( )
A.66 B.64 C.62 D.60
【分析】原式利用完全平方公式变形,将已知等式代入计算即可求出值.
【解答】解:∵x+=8,
∴原式=(x+)2﹣2=64﹣2=62.
故选:C.
8.(3分)下列命题中,是假命题的是( )
A.全等三角形的对应边相等
B.三角形的一个外角大于任何一个内角
C.有一个角等于60°的等腰三角形是等边三角形
D.一个数的立方根等于他本身,则这个数是﹣1,0,1
【分析】根据全等三角形的性质,三角形的外角的性质,等边三角形的判定,立方根的定义一一判断即可.
【解答】解:A、全等三角形的对应边相等,是真命题,本选项不符合题意;
B、三角形的一个外角大于任何一个内角,是假命题,应该是三角形的一个外角大于任何和 它不相邻一个内角,本选项符合题意;
C、有一个角等于60°的等腰三角形是等边三角形,是真命题,本选项不符合题意;
D、一个数的立方根等于它本身,则这个数是﹣1,0,1,是真命题,本选项不符合题意.
故选:B.
9.(3分)如果用换元法解分式方程,并设,那么原方程可化为( )
A. B. C. D.y+
【分析】设,则=,再把方程变形求解.
【解答】解:设,
原方程可化为:y﹣+3=0,
故选:B.
10.(3分)如图,DE,DF分别是线段AB,BC的垂直平分线,连接AD,CD,则下列结论正确的是( )
A.AD=CD B.∠A=∠C C.∠B=∠ADC D.DE=DF
【分析】根据线段垂直平分线的性质得出AD=BD,CD=BD,求出AD=BD=CD,根据等边对等角得出∠A=∠2,∠1=∠C,再逐个判断即可.
【解答】解:连接BD,如图1,
∵DE,DF分别是线段AB,BC的垂直平分线,
∴AD=BD,CD=BD,
即AD=BD=CD,
∴∠A=∠2,∠1=∠C,
不能推出∠A和∠C相等,∠ABC和∠ADC相等,DE和DF相等,
故选:A.
11.(3分)甲、乙两人完成一项工作,甲先做了3天,然后乙加入合作,完成剩下的工作,设工作总量为1,工作进度如表:
天数 第3天 第5天
工作进度
若乙单独完成这项工作,则需要( )
A.9天 B.10天 C.12天 D.24天
【分析】求出甲单独完成这项工程所需时间,设乙单独完成这项工作需x天,根据甲完成的部分+乙完成的部分=这项工程的,列出分式方程,解方程即可.
【解答】解:甲单独完成这项工作所需天数为3÷=12(天).
设乙单独完成这项工作需x天,
依题意,得:+=,
解得:x=24
经检验,x=24是原方程的解,且符合题意.
故选:D.
12.(3分)如图,在△ABC和△ADE中,∠CAB=∠DAE=36°,AB=AC,AD=AE.连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分∠ABC,则下列结论错误的是( )
A.∠ADC=∠AEB B.CD∥AB C.DE=GE D.CD=BE
【分析】利用AAS证明△DAC≌△EAB可得∠ADC=∠AEB,CD=BE,可判断A,D选项正确;由全等三角形的性质,三角形的内角和定理及等腰三角形的性质可求解∠ACB的度数,利用角平分线的定义求得∠ACD=∠ABE=36°,即可得∠ACD=∠CAB,进而可证明CD∥AB,即可判断B选项正确,进而可求解.
【解答】解:A.∵∠CAB=∠DAE=36°,
∴∠CAB﹣∠CAE=∠DAE﹣∠CAE,即∠DAC=∠EAB,
在△DAC和△EAB中,
,
∴△DAC≌△EAB(SAS),
∴∠ADC=∠AEB,故A选项不符合题意;
CD=BE,故D选项不符合题意;
B.∵AC=AB,
∴∠ACB=∠ABC,
∵∠CAB=∠DAE=36°,
∴∠ACB=∠ABC=(180°﹣36°)÷2=72°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=36°,
∴∠ACD=∠ABE=36,
∵∠DCA=∠CAB=36°,
∴CD∥AB(内错角相等,两直线平行),
故B选项不符合题意;
C.根据已知条件无法证明DE=GE,故C选项符合题意.
故选:C.
二、填空题(本大题共6小题,每小题3分,共18分)
13.(3分)分式没有意义,则x的值为 1 .
【分析】根据分式有意义的条件即可求出答案.
【解答】解:当2x﹣2=0时,此时分式无意义,
∴x=1,
故答案为:x=1.
14.(3分)人体细胞的平均直径为0.000105微米,用科学记数法可表示为 1.05×10﹣4 微米.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:0.000105微米=1.05×10﹣4微米.
故答案为:1.05×10﹣4.
15.(3分)如图,l1∥l2,AE⊥BE于点E.若∠2=140°,则∠1的度数为 130° .
【分析】根据平角的定义得出∠4=40°,根据平行线的性质得出∠3=∠4,由垂直的定义求出∠AEB的度数,最后根据三角形外角的性质得出∠1的度数.
【解答】解:如图:
∵∠2=140°,∠4+∠2=180°,
∴∠4=180°﹣∠2=40°,
∵AE⊥BE,
∴∠AEB=90°.
∵l1∥l2,
∴∠3=∠4=40°,
∴∠1=∠3+∠AEB=40°+90°=130°.
故答案为:130°.
16.(3分)如图,点P在等边三角形ABC的内部,PD⊥BC,PE⊥AC,PF⊥AB,垂足分别为D,E,F,若PD+PE+PF=4,且S△ABC=16,则△ABC的边长为 8 .
【分析】连接AP,BP,PC,根据S△ABC=AB×PF+×AC×PE+BC×PD=×AB×(PF+PE+PD),求解即可.
【解答】解:连接AP,BP,PC,
∵△ABC是等边三角形,
∴AB=BC=AC,
∵S△ABC=AB×PF+×AC×PE+BC×PD=×AB×(PF+PE+PD)=16,PD+PE+PF=4
∴AB=8,
故答案为8.
17.(3分)对于非零的两个实数a,b,规定a*b=,若5*(3x﹣1)=2,则x的值为 .
【分析】根据规定,把5*(3x﹣1)=2,转化为我们学过的方程,再求解即可.
【解答】解:∵a*b=,5*(3x﹣1)=2,
∴﹣=2,
去分母得,15﹣2(3x﹣1)=10(3x﹣1),
整理得,36x=27,
解得x=,
经检验,x=是原方程的解,
故答案为.
18.(3分)如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm的速度沿BC向点C运动,点Q从点C出发,以vcm/s的速度沿CA向点A运动,当v= 4或4.8 时,△ABP与△PQC全等.
【分析】分两种情况①当BP=CQ,AB=PC时,△ABP≌△PCQ;②当BA=CQ,PB=PC时,△ABP≌△QCP,然后分别计算出t的值,进而得到v的值.
【解答】解:设运动时间为t秒,
∵点P从点B出发,以2cm的速度沿BC向点C运动,点Q从点C出发,以vcm/s的速度沿CA向点A运动,
∴BP=2t(cm),CQ=vt(cm),
∴PC=10﹣2t(cm),
∵AB=AC,
∴∠B=∠C,
当BP=CQ,AB=PC时,△ABP≌△PCQ,
∴AB=PC=6cm,
∴BP=4cm=CQ,
∴2t=4,
解得:t=2,
∴v==2;
②当BA=CQ=6cm,PB=PC时,△ABP≌△QCP,
∵PB=PC,
∴BP=PC=BC=5cm,
∴2t=5,
解得:t=2.5,
∴v==2.4,
解得:v=2.4,
综上所述:当v=2或2.4时△ABP与△PQC全等,
故答案为:2或2.4.
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
19.(6分)计算.
【分析】根据有理数的乘方、零指数幂、负整数指数幂以及绝对值的性质分别进行计算,即可得出答案.
【解答】解:
=﹣1+1+2﹣3
=﹣1.
20.(6分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图,∠α,和线段a.求作:Rt△ABC,使∠BAC=∠α,∠ACB=90°,斜边AB=a.
【分析】先作∠MAN=∠α,再在AM上截取AB=a,然后过B点作AN的垂线,垂足为C点,则△ABC满足条件.
【解答】解:如图,Rt△ABC为所作.
21.(10分)(1)计算:÷+.
(2)解方程.
【分析】(1)原式利用除法法则变形,约分后利用同分母分式的加法法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:(1)原式= (a+1)(a﹣1)+=+==2;
(2)去分母得:x﹣3+x﹣2=3,
解得:x=4,
经检验x=4是分式方程的解.
22.(6分)如图,在△ABC中,AB=AC,D是BC边上一点,EF垂直平分CD,交AC于点E,交BC于点F,连接DE.若∠A=56°,求∠DEC的度数.
【分析】根据线段垂直平分线的性质可得∠EDC=∠ECD,根据等腰三角形的性质进一步可得∠EDC=∠ABC,根据平行线的性质可得∠DEC的度数,根据等腰三角形的性质即可求出∠DEF的度数.
【解答】解:∵EF垂直平分CD,
∴ED=EC,
∴∠EDC=∠ECD,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EDC=∠ABC,
∴DE∥AB;
∵DE∥AB,∠A=56°,
∴∠DEC=∠A=56°,
23.(8分)阅读理解题.
(1)观察:,,……,填空:= ﹣ ;
(2)填空:= ;
(3)利用上述规律解分式方程:.
【分析】(1)根据前三个式子的结果直接写出答案;
(2)根据以上等式的规律直接写出答案;
(3)根据规律变形,然后解分式方程即可.
【解答】解:(1)=﹣;
故答案为:﹣;
(2)
=1﹣+﹣+…+﹣
=1﹣
=,
故答案为:;
(3),
1﹣=2﹣,
去分母得:x+1﹣1=2x+2﹣7
解得:x=5,
经检验:x=5是方程的根,
∴原方程的解为x=5.
24.(8分)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.
【分析】先猜想AP=CQ,再在△ABP与△CBQ中,由AB=CB,BP=BQ,∠ABC=∠PBQ=60°可得出∠ABP=∠CBQ,进而可判断出△ABP≌△CBQ,由全等三角形的对应边相等即可得出结论.
【解答】猜想:AP=CQ
证明:在△ABP与△CBQ中,
∵AB=CB,BP=BQ,∠ABC=∠PBQ=60°,
∴∠ABP=∠ABC﹣∠PBC=∠PBQ﹣∠PBC=∠CBQ,
∴△ABP≌△CBQ,
∴AP=CQ
25.(10分)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米?
【分析】(1)根据题意可知:甲原来工作5天的工作量+后来2天的工作量=600,可以列出相应的方程,然后求解即可;
(2)根据题意可知:甲、乙施工的长度都是900米,再根据题意可知,两个工程队施工天数相同,即可列出相应的分式方程,然后求解即可,注意分式方程要检验.
【解答】解:(1)设甲施工队增加人员后每天修建灌溉水渠x米,则原计划每天施工(x﹣20)米,
由题意可得:5(x﹣20)+2x=600,
解得x=100,
答:甲施工队增加人员后每天修建灌溉水渠100米;
(2)设乙施工队原来每天修建灌溉水渠m米,则技术更新后每天修建水渠m(1+20%)=1.2m米,
由题意可得:,
解得m=90,
经检验,m=90是原分式方程的解,
答:乙施工队原来每天修建灌溉水渠90米.
26.(12分)已知AD是等边△ABC的高,F为AC边上的一个动点(不与A、C重合),BF与AD相交于点E,连接CE.
(1)求证:BE=CE;
(2)当△AEF是以AE为腰的等腰三角形时,求∠ECD的度数;
(3)作∠FEG=120°,交AB于点G,猜想EF、EG的数量关系并说明理由.
【分析】(1)先判断出AD是BC的垂直平分线,即可得出结论;
(2)先判断出等腰三角形AEF的腰,再用等腰三角形的性质和三角形的外角的性质即可得出结论;
(3)先判断出,∠AFE=BGE,进而构造出全等三角形,即可得出结论.
【解答】(1)证明:∵AD是等边△ABC的高,
∴AD是BC的垂直平分线,
∵点E在AD上,
∴BE=CE;
(2)解:∵AD是等边△ABC的高,
∴∠CAD=∠BAC=30°,
∵△AEF为等腰三角形,AE为腰,
∴AE=AF,
∴∠AEF=∠AFE=75°,
∵∠ACB=60°,
∴∠CBF=∠AFE﹣∠ACB=75°﹣60°=15°,
∵BE=CE,
∴∠ECD=∠CBF=15°;
(3)解:结论:EF=EG,
理由:∵∠BAC=60°,∠FEG=120°,
∴∠BAC+∠FEG=180°,
∴∠AGE+∠AFE=180°,
∴∠AFE=BGE,
过点E作EN⊥AB,EM⊥AC,
∵AD是∠BAC的平分线,
∴EN=EM;
在△ENG和△EMF中,
,
∴△ENG≌△EMF,
∴EG=EF.
同课章节目录
