不等式的恒成立问题[上学期]

课件23张PPT。不等式应用（二）------不 等式中恒成立的问题班 级：高三（7）
主讲者：林根新1.已知 不等式（a-2)x2+2(a-2)x-4<0,对一切实数恒成立，则a的取值范围为( )练习：C1.已知 不等式（a-2)x2+2(a-2)x-4<0,对一切实数恒成立，则a的取值范围为( )分析一：排除法
（选择题的特点）比较选择支，-2，2代入检验1.已知 不等式（a-2)x2+2(a-2)x-4<0,对一切实数恒成立，则a的取值范围为( )二、直接法不等式是一次的还是二次的？分类讨论若a 2时，若a=2时，-4〈0恒成立不等式解集法2.已知两个正数x,y满足x+y=1,则使不等式 恒成立的实数m的取值范围是__________
分析:2.已知两个正数x,y满足x+y=1,则使不等式 恒成立的实数m的取值范围是__________法一：“1”的活用
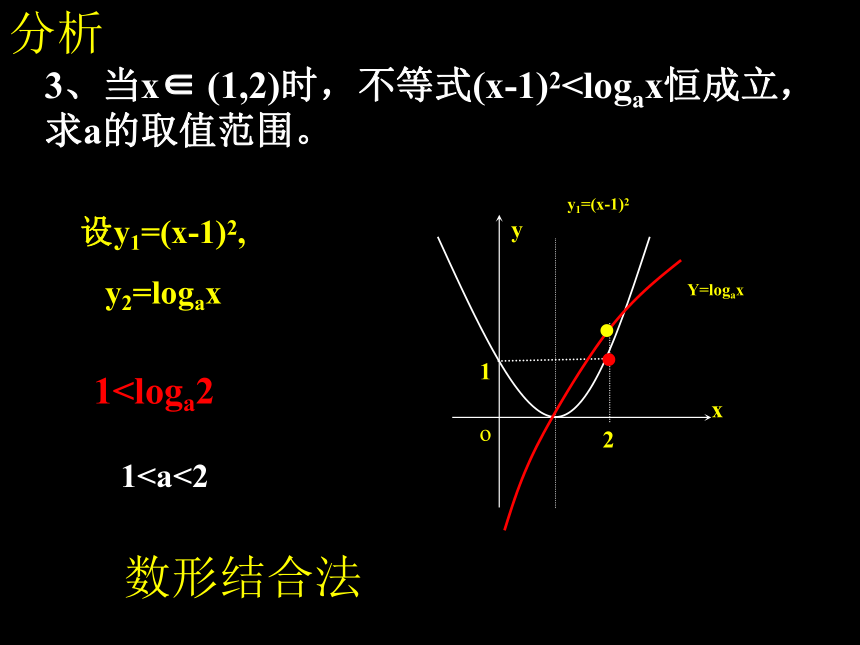
法二：消元求最值练习3：当x∈ (1,2)时，不等式(x-1)2 y2=logax1a恒成立, 则a的取值范围是 .例2：关于x的不等式
在区间［ 2,3］上恒成立，求实数m的取值范围.
1解：据题意，=81-8m≥0由已知得: ∴ m≤923则 ∴ ∴m≤9据题意：函数f(x)＝2x2-9x+m在[2，3]的图象始终位于X轴的下方或X轴上，即与x轴的两交点分别在区间(-∞, 2］，［3，+∞)内，2解：..∴m-9≤0, 即m≤9问题等价于f(x)max≤0≤f(3)=m-9.则问题m≤g(x)min∴ m≤9x 　 [2,3]4解：变量分离法x4+1 ≥ mx2变式１. x4-mx2+1 ≥ 0在R上恒成立，求ｍ的取值范围。 　x=0时，满足条件，m≤2x≠0时，m≤x2+1/x2
变式３. mx2-x-m+1<0对满足 的所有ｍ都成立，求ｘ的取值范围。 |m|≤2设f(m)=(x2-1)m-x+1 思考题 已知函数f(x)是定义在区间 上的减函数，是否存在实数m使得
对于定义域内的一切实数 均成立。若存在，求出m的取值范围；若不存在说明理由。
恒成立常用方法:(一):不等式解集法:
(二):函数最值法.
(三):数形结合思想
(四):参数分离法.课堂小结中学数学中的恒成立的问题一般运用函数或借助于函数的图象转化为解方程和解不等式问题。与不等式有关的恒成立的问题通常又和函数最值、函数图象以及不等式解集直接相关，而解题思想方法是函数与方程、数形 结合以及等价转化。因此需要同学们平时多加以思考和总结。恒成立常用方法:(一):不等式解集法:
(二):函数最值法.
(三):数形结合思想
(四):参数分离法.Good bye!!谢 谢