一元二次不等式的复习课[上学期]
文档属性
| 名称 | 一元二次不等式的复习课[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 587.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-02-01 00:00:00 | ||
图片预览






文档简介
课件15张PPT。
一元二次不等式解法
2006年9月淄博七中 高二数学组
主讲:杨德怀一、预习一元二次不等式解法 利用函数把方程与不等式联系起来,这样我们可以通过对二次函数的研究,来讨论方程的解,根据方程的解进一步来解一元二次不等式。 二次函数、一元二次方程、一元二次不等式是一个有机的整体。 引例.画出函数y=x2-x-6的图象,并根据图象回答:
(1).图象与x轴交点的坐标为 ,
该坐标与方程 x2 -x-6=0的解有什么关系: 。
(2).当x取 时,y=0?
当x取 时,y>0?
当x取 时,y<0?
(3).由图象写出:
不等式x2 -x-6>0 的
解集为 。
不等式x2 -x-6<0 的
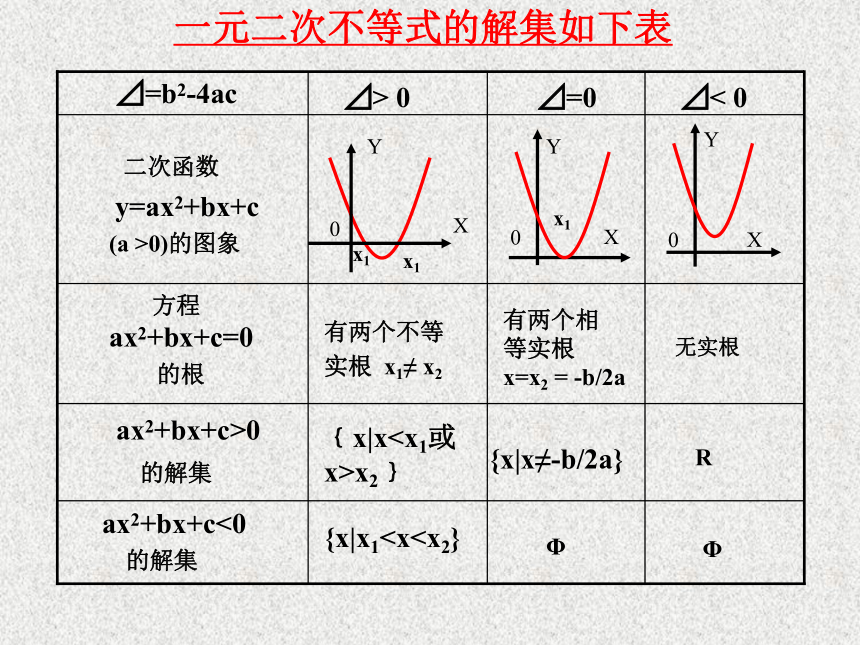
解集为 。(-2, 0),(3, 0) 交点的横坐标即为方程的根x= -2 或 3x<-2 或 x>3 -2 < x <3﹛x|x<-2或x>3﹜﹛x| -2 0⊿=0 ⊿< 0 二次函数
y=ax2+bx+c
(a >0)的图象 方程ax2+bx+c=0
的根ax2+bx+c>0
的解集 ax2+bx+c<0
的解集有两个不等
实根 x1≠ x2有两个相
等实根
x=x2 = -b/2a无实根﹛x|xx>x2﹜{x|x≠-b/2a}R{x|x1 0 方程x2-2x-15=0的两根为:
x=-3,或x=5∴ 不等式的解集
为:{x│ x ≤-3 或x ≥5}。 解一元二次不等式的方法步骤是: (3)根据图象写出解集 步骤:(1)化成标准形式 (a>0):
ax2+bx+c>0 或 ax2+bx+c<0 (2)求⊿,解方程,画图象; 方法:数形结合二、二次不等式的简单应用 解法1:(换元法)
设│x│ =t,则t ≥ 0原不等式可化为
t2 -2t-15≥0
由例1 可知解为t≥5或t≤-3
∵t ≥ 0 ∴ 不等式的解集为{t│t≥5 }
∴ │x│≥5
∴原不等式的解为{x│x≥5或x≤-5 }。例1 、解不等式: 分析1:不同于x2-2x-15≥0的根本点在于不
等式中含│x│,由于│x│ 2 = x2 ,则可以通过换
元令│x│ =t,将不等式转化为t 2-2 t -15≥0求解。x2-2 x -15≥0x2-2│x│-15≥0 解法2:当x>0时,
原不等式可化为x2 -2x-15≥0
则不等式的解为x≥5或 x≤-3
∵x>0 ∴ 不等式的解集为{x│x≥5 } 当x ≤0时,
原不等式可化为x2 +2x-15≥0
则不等式的解为x≥3或x ≤-5
∵x≤0 ∴ 不等式的解集为{x│x≤-5 }
由以上可知原不等式的解为{x│x≥5或x≤-5 }。 分析2:也可用绝对值定义去掉绝对值将不等式转化为不含绝对值的求解。例1 、解不等式: x2-2│x│-15≥0 例2 . 已知一元二次不等式a x2 +bx+6>0
的解集为{x │- 2 <x<3}, 求a-b的值. 解:由条件可知 :
方程a x2 +bx+6=0的根-2,3
又解在两根之间; 分析:二次不等式的解是通过二次方程的根来确定的,∴a<0∵ 6 /a = -2× 3= -6 ∴ a=-1
∵ b /a = -2+3=1 ∴ b=1
则a-b=-2 由此可以理解为 a x2 +bx+6=0
的根为-2,3。 例2 . 已知一元二次不等式a x2 +bx+6>0
的解集为{x │- 2 <x<3}, 求a-b的值. 另解:由条件可知 :
方程 a x2 +bx+6=0的根-2、3 ,
代入方程可得:则a-b=-2 例3、已知集合A={x│ x2 -(a+1)x+a≤0 } ,
B={x│1≤x≤3},若A∩B=A , 求实数a取值范围。解:A ∩B=A,则 A B∩若a>1 , 则A={ x│ 1≤x≤a } , 若a<1 , 则 A={ x │ a ≤ x≤ 1 },∴a取值范围是1≤a≤3则 1 < a≤3那么, A不可能是B的子集 ;分析: 观察不难发现:a、1是 x2 -(a+1)x +a=0的根. 若a=1 , 则A={ 1 },满足条件 ; ∴a =1 例4. 函数f(x)= lg(kx2 -6kx+k+8) 的定义域为R , 求k的取值范围 解:∵f(x)= lg(kx2 -6kx+k+8)
的定义域为R , 即△=(6k)2-4k(k+8)
=32k2-32K< 0
∴ 0 < k < 1分析:令u= kx2 -6kx+k+8, 对任意的x,u= kx2-6kx+k+8的值恒大于0函数u= kx2-6kx+k+8的图象恒在x轴的上方函数f(x) 的定义域为R∴ k ≥ 0当k=0时,f(x)=lg8 满足条件.当k> 0时,∴只要△ < 0∴f(x)的定义域为R时, k的取值范围为0 ≤ k < 1 例4. 函数f(x)= lg(kx2 -6kx+k+8) 的定义域为R , 求k的取值范围 问题:函数f(x)= lg(kx2 -6kx+k+8) 的值域为R , 求k的取值范围。思考三、小结: 四、作业:⒉一元二次不等式的简单应用⒈一元二次不等式的解法; 1、若A={x│-1≤x≤1}, B={x | x2 + (a+1)x +a≤0},若A∩B=B,求a的取值范围。
2、函数的f(x)= 定义域为R求a的取值范围。
3、求函数y= x2+2ax-3 ,x ∈[0,2]的最值。谢 谢 指 导同学们 再见!
一元二次不等式解法
2006年9月淄博七中 高二数学组
主讲:杨德怀一、预习一元二次不等式解法 利用函数把方程与不等式联系起来,这样我们可以通过对二次函数的研究,来讨论方程的解,根据方程的解进一步来解一元二次不等式。 二次函数、一元二次方程、一元二次不等式是一个有机的整体。 引例.画出函数y=x2-x-6的图象,并根据图象回答:
(1).图象与x轴交点的坐标为 ,
该坐标与方程 x2 -x-6=0的解有什么关系: 。
(2).当x取 时,y=0?
当x取 时,y>0?
当x取 时,y<0?
(3).由图象写出:
不等式x2 -x-6>0 的
解集为 。
不等式x2 -x-6<0 的
解集为 。(-2, 0),(3, 0) 交点的横坐标即为方程的根x= -2 或 3x<-2 或 x>3 -2 < x <3﹛x|x<-2或x>3﹜﹛x| -2
y=ax2+bx+c
(a >0)的图象 方程ax2+bx+c=0
的根ax2+bx+c>0
的解集 ax2+bx+c<0
的解集有两个不等
实根 x1≠ x2有两个相
等实根
x=x2 = -b/2a无实根﹛x|x
x=-3,或x=5∴ 不等式的解集
为:{x│ x ≤-3 或x ≥5}。 解一元二次不等式的方法步骤是: (3)根据图象写出解集 步骤:(1)化成标准形式 (a>0):
ax2+bx+c>0 或 ax2+bx+c<0 (2)求⊿,解方程,画图象; 方法:数形结合二、二次不等式的简单应用 解法1:(换元法)
设│x│ =t,则t ≥ 0原不等式可化为
t2 -2t-15≥0
由例1 可知解为t≥5或t≤-3
∵t ≥ 0 ∴ 不等式的解集为{t│t≥5 }
∴ │x│≥5
∴原不等式的解为{x│x≥5或x≤-5 }。例1 、解不等式: 分析1:不同于x2-2x-15≥0的根本点在于不
等式中含│x│,由于│x│ 2 = x2 ,则可以通过换
元令│x│ =t,将不等式转化为t 2-2 t -15≥0求解。x2-2 x -15≥0x2-2│x│-15≥0 解法2:当x>0时,
原不等式可化为x2 -2x-15≥0
则不等式的解为x≥5或 x≤-3
∵x>0 ∴ 不等式的解集为{x│x≥5 } 当x ≤0时,
原不等式可化为x2 +2x-15≥0
则不等式的解为x≥3或x ≤-5
∵x≤0 ∴ 不等式的解集为{x│x≤-5 }
由以上可知原不等式的解为{x│x≥5或x≤-5 }。 分析2:也可用绝对值定义去掉绝对值将不等式转化为不含绝对值的求解。例1 、解不等式: x2-2│x│-15≥0 例2 . 已知一元二次不等式a x2 +bx+6>0
的解集为{x │- 2 <x<3}, 求a-b的值. 解:由条件可知 :
方程a x2 +bx+6=0的根-2,3
又解在两根之间; 分析:二次不等式的解是通过二次方程的根来确定的,∴a<0∵ 6 /a = -2× 3= -6 ∴ a=-1
∵ b /a = -2+3=1 ∴ b=1
则a-b=-2 由此可以理解为 a x2 +bx+6=0
的根为-2,3。 例2 . 已知一元二次不等式a x2 +bx+6>0
的解集为{x │- 2 <x<3}, 求a-b的值. 另解:由条件可知 :
方程 a x2 +bx+6=0的根-2、3 ,
代入方程可得:则a-b=-2 例3、已知集合A={x│ x2 -(a+1)x+a≤0 } ,
B={x│1≤x≤3},若A∩B=A , 求实数a取值范围。解:A ∩B=A,则 A B∩若a>1 , 则A={ x│ 1≤x≤a } , 若a<1 , 则 A={ x │ a ≤ x≤ 1 },∴a取值范围是1≤a≤3则 1 < a≤3那么, A不可能是B的子集 ;分析: 观察不难发现:a、1是 x2 -(a+1)x +a=0的根. 若a=1 , 则A={ 1 },满足条件 ; ∴a =1 例4. 函数f(x)= lg(kx2 -6kx+k+8) 的定义域为R , 求k的取值范围 解:∵f(x)= lg(kx2 -6kx+k+8)
的定义域为R , 即△=(6k)2-4k(k+8)
=32k2-32K< 0
∴ 0 < k < 1分析:令u= kx2 -6kx+k+8, 对任意的x,u= kx2-6kx+k+8的值恒大于0函数u= kx2-6kx+k+8的图象恒在x轴的上方函数f(x) 的定义域为R∴ k ≥ 0当k=0时,f(x)=lg8 满足条件.当k> 0时,∴只要△ < 0∴f(x)的定义域为R时, k的取值范围为0 ≤ k < 1 例4. 函数f(x)= lg(kx2 -6kx+k+8) 的定义域为R , 求k的取值范围 问题:函数f(x)= lg(kx2 -6kx+k+8) 的值域为R , 求k的取值范围。思考三、小结: 四、作业:⒉一元二次不等式的简单应用⒈一元二次不等式的解法; 1、若A={x│-1≤x≤1}, B={x | x2 + (a+1)x +a≤0},若A∩B=B,求a的取值范围。
2、函数的f(x)= 定义域为R求a的取值范围。
3、求函数y= x2+2ax-3 ,x ∈[0,2]的最值。谢 谢 指 导同学们 再见!
