绝对值不等式[上学期]

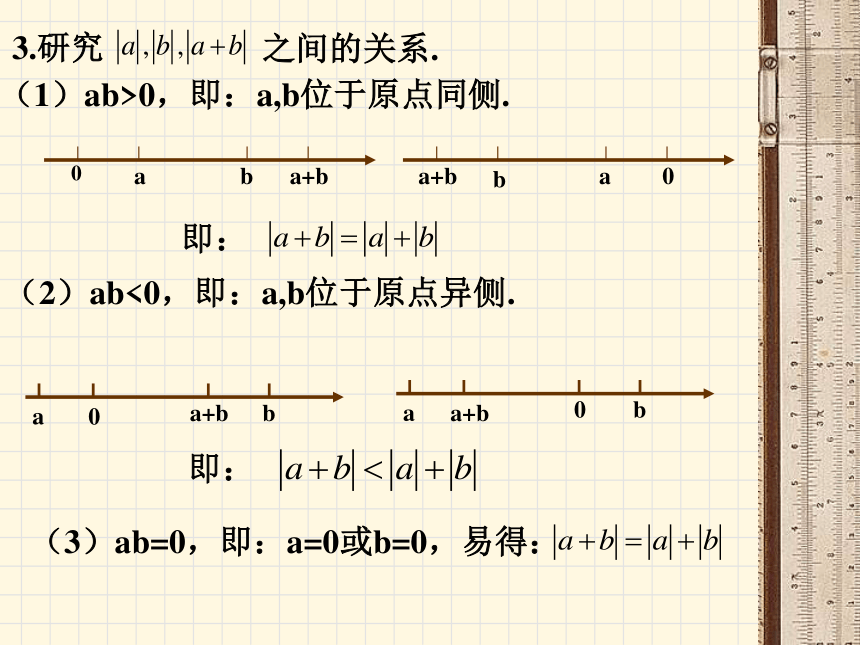
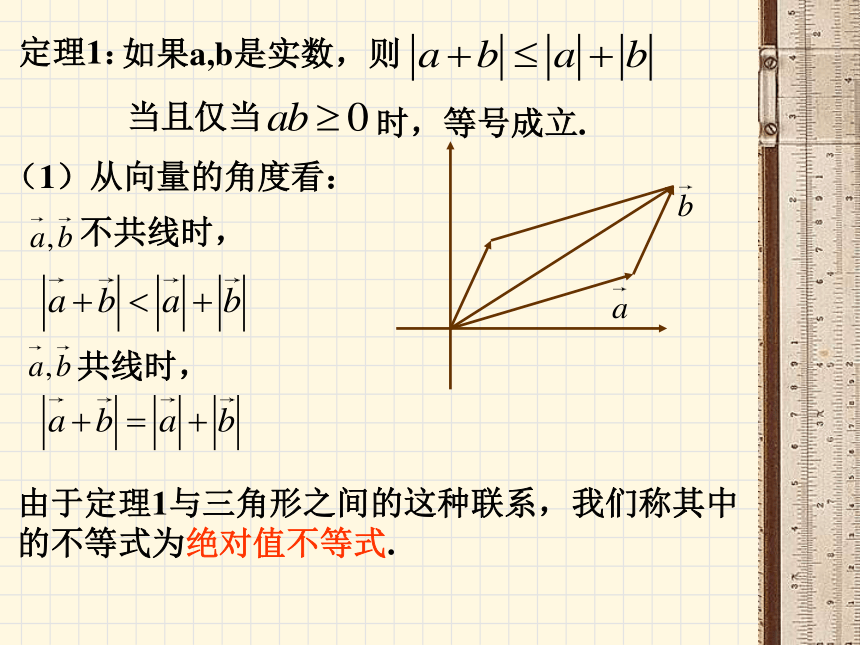
课件15张PPT。绝对值不等式1.实数a的绝对值 的几何意义：a所对应的点到原点的距离.2. 的几何意义：数轴上A、B两点之间的距离.3.研究之间的关系.（1）ab>0，即：a,b位于原点同侧.即：（2）ab<0，即：a,b位于原点异侧.即：（3）ab=0，即：a=0或b=0，易得：定理1： 如果a,b是实数，则当且仅当时，等号成立.（1）从向量的角度看：不共线时，由于定理1与三角形之间的这种联系，我们称其中
的不等式为绝对值不等式.共线时，（2）从代数的角度进行证明：所以，，当且仅当时，等号成立.？能否根据定理1的研究思想，探究之间的关系.（1）（2）之间的关系.定理2 如果a,b是实数，则前一个等号成立条件：后一个等号成立条件：几何意义：三角形两边和大于第三边，
两边差小于第三边.定理2 如果a,b,c是实数，那么几何解释：例1 已知，求证：练习：1.若,下列不等式中一定成立的是（ ）2.若，则下列不等式一定成立的是例2 设求证：练习：1.解关于x 的不等式：(a>1)2.已知，求证：3.已知关于实数x的二次方程有两个实根求证：例3 两个施工队分别被安排在公路沿线的两个地点
施工，这两个地点分别位于公路路碑的第10km，
和第20km处，现要在公路沿线建两个施工队的
共同临时生活区，每个施工队每天在生活区和
施工地点之间往返一次，要使两个施工队每天
往返的路程之和最小，生活区应该建于何处？2.绝对值不等式的解法：一般的，a>0，那么从绝对值的意义看，表示数轴上到原点距离小于a的点的集合.表示数轴上到原点距离大于a的点的集合.（1）的解法.例3 解不等式：变式：解不等式：例4 解不等式：例5 解不等式：练习：解不等式：（2）型如例5 解不等式：练习：1.解不等式：（1）（2）2.对于任意x不等式恒成立，则实数a的取值范围_______.3.不等式的解集非空，则实数a的取值范围是______例6 解不等式：